当前位置：首页 > news >正文

HyperPlonk 的硬件友好性

news 2025/9/1 12:43:10

1. 引言

在工业界广泛使用的 Plonk SNARK 协议高度依赖 NTT 来完成计算。HyperPlonk 是 Plonk 的一个变种，它试图通过用 Sumcheck 替代 NTT（以及其它改进）来提升并行性。Ingonyama团队认为：

Sumcheck 在 HyperPlonk 中所谓的并行化优势可能被高估了。其根本问题在于：
- Sumcheck 的主要瓶颈并不在于计算，而是 内存访问。

本文从硬件角度来讨论 2023年论文HyperPlonk: Plonk with Linear-Time Prover and High-Degree Custom Gates，重点关注 HyperPlonk 的硬件友好性：

主要关注其核心构件 —— Multivariate多变量 SumCheck 协议，并将其计算与内存复杂度和 NTT（Number Theoretic Transform，数论变换）进行比较。
指出 Sumcheck 的性能瓶颈并非源于纯粹的计算量，而是源于内存访问模式。这是一个关键性的区分：
- 理想情况下，像 Sumcheck 这样的密码学协议应该是 计算受限（compute-bound） 的，而不是 内存受限（memory-bound） 的。
- 因为现代硬件——尤其是 GPU 和专用加速器——在高吞吐量算术运算方面高度优化，但在受制于内存带宽时却往往表现不佳。

这种 内存受限行为 在 数论变换（NTT） 的使用中尤为明显。NTT 是 Sumcheck 中多项式运算的基本构件。虽然 NTT 具有高度并行化的潜力，但它需要频繁且结构化地访问大量域元素数组，这对内存子系统和缓存层次结构带来了巨大的压力。结果是，即便底层的算术运算相对便宜，内存访问开销 仍可能主导整体性能。

要解决这一局限，需要：

优化 内存布局
采用 硬件感知的调度策略，
并在系统设计层面重新思考，从而推动硬件发挥其 计算极限，而不是被 内存天花板 所限制。

本文通过对 ICICLE（https://github.com/ingonyama-zk/icicle）中 Sumcheck 实现的 性能剖析，提供了确凿的证据，证明内存访问确实是主要瓶颈，并提出了可为未来的 Sumcheck 及类似协议优化与硬件加速提供参考的见解。

本文只关注了 “标准 SumCheck” 的结构，而没有讨论其可能的改进空间。与 NTT 相比，SumCheck 的硬件加速问题几乎没有被深入研究过。很可能已经存在，或未来会出现一些方法来提升 SumCheck 的硬件友好性：

密码学层面 —— 如 Fiat-Shamir 在其中的作用
SumCheck 新变种
协议设计高层次的并行化思路 ——（其中一些已经在 HyperPlonk 论文中提出，比如批处理 Batching）

2. 背景 - HyperPlonk

Plonk 是业界最广泛应用的 SNARK 之一。在标准的 Plonk 中，经过算术化（arithmetization）后，得到的执行轨迹会被插值为单变量多项式，因此协议大量依赖 NTT。

HyperPlonk 是 Plonk 的一种新变体，它将执行轨迹插值在 boolean hypercube（布尔超立方体）上，因此其执行轨迹的多项式表示是一个多变量多项式，并且在每个变量上的阶数都是 1。这种表示被称为 MLE（MultiLinear Extension，多线性扩展）。关于 HyperPlonk 的一个很好的综述，可以参考 Benedikt Bunz 2022年10月在 ZKSummit8 的演讲ZK8: Hyperplonk: PLONK without FFTs and with high degree gates - Benedikt Bünz 。

HyperPlonk 的一个关键优势是：

消除了大规模 NTT，

而大规模 NTT 是 Plonk 在大电路中最大的计算瓶颈。通过转移到布尔超立方体，不再需要单变量多项式。相反，HyperPlonk 依赖于多变量多项式运算。在 HyperPlonk 论文的第 3 节中，作者专门开发了一套处理多变量多项式的工具箱。下图（取自论文）展示了 HyperPlonk 是如何基于这套工具箱构建的。可以看到，在最底层，核心就是经典的 SumCheck 协议，它必然会成为 HyperPlonk 的主要计算难点（忽略多项式承诺部分），完全替代了 NTT。
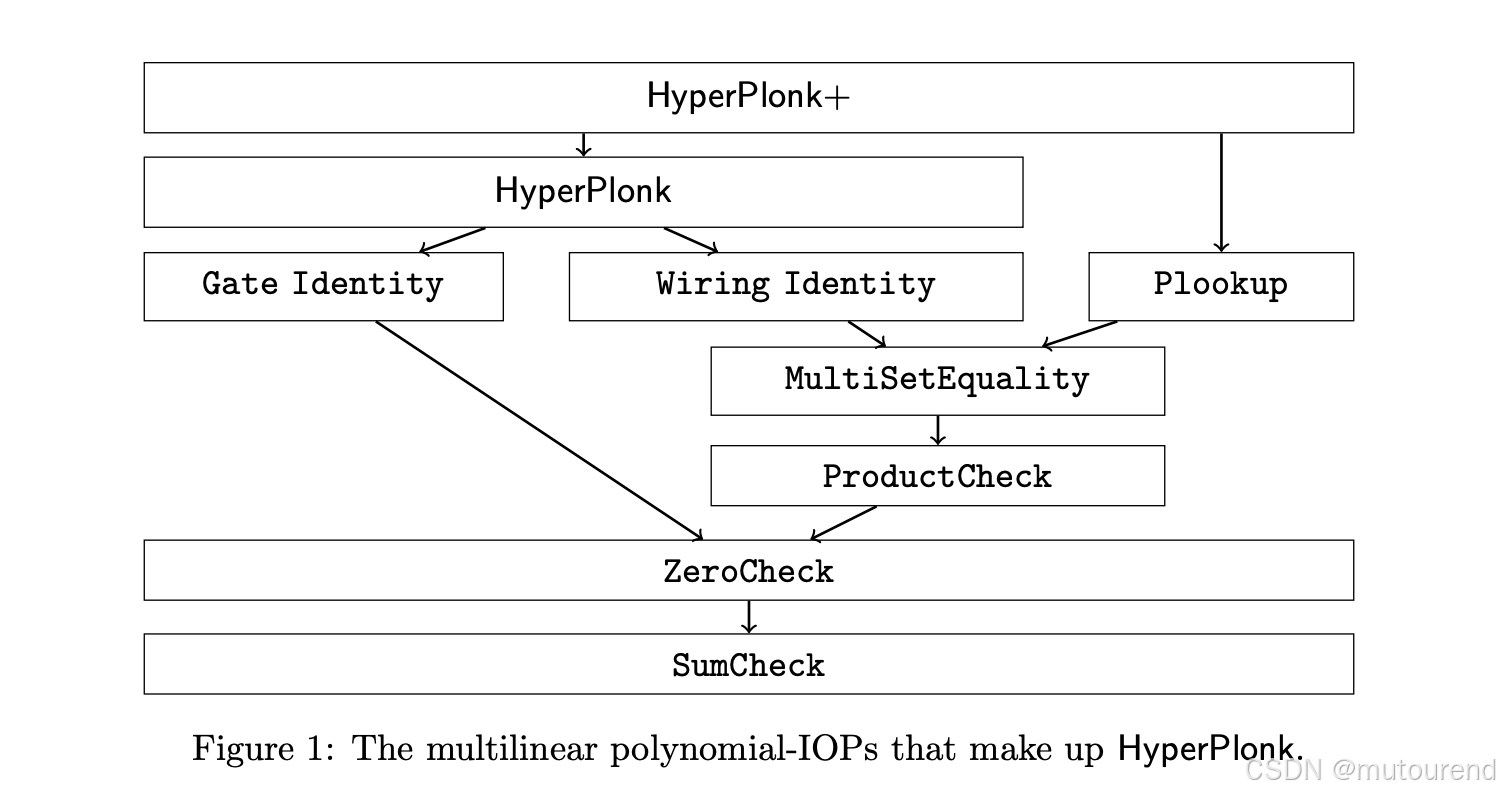
在这里插入图片描述

3. HyperPlonk 中的 SumCheck

3.1 HyperPlonk 中的 SumCheck 简单示例

考虑一个展开为向量形式的执行轨迹。用长度为 8 的向量来说明这个想法，该向量由多项式的取值组成：
${fi}i=07,fi∈F.\{ f_i \}_{i=0}^7, \quad f_i \in \mathbb{F}.$

用多变量多项式 $F(X_3,X_2,X_1)$ 来插值这些值，如下表所示：

$f_0$	$f_1$	$f_2$	$f_3$	$f_4$	$f_5$	$f_6$	$f_7$
$F (0, 0, 0)$	$F (0, 0, 1)$	$F (0, 1, 0)$	$F (0, 1, 1)$	$F (1, 0, 0)$	$F (1, 0, 1)$	$F (1, 1, 0)$	$F (1, 1, 1)$

第一行是有限域元素，第二行表示插值的对应关系。用拉格朗日插值来表达：
$F(X3,X2,X1)=f0(1−X3)(1−X2)(1−X1)+f1(1−X3)(1−X2)X1+f2(1−X3)X2(1−X1)+f3(1−X3)X2X1+f4X3(1−X2)(1−X1)+f5X3(1−X2)X1+f6X3X2(1−X1)+f7X3X2X1\begin{aligned} F(X_3,X_2,X_1) &= f_0(1-X_3)(1-X_2)(1-X_1) + f_1(1-X_3)(1-X_2)X_1 \\ &\quad + f_2(1-X_3)X_2(1-X_1) + f_3(1-X_3)X_2X_1 \\ &\quad + f_4X_3(1-X_2)(1-X_1) + f_5X_3(1-X_2)X_1 \\ &\quad + f_6X_3X_2(1-X_1) + f_7X_3X_2X_1 \end{aligned}$

其中， $X$ 和 $1 - X$ 是定义在二元域上的Lagrange base polynomial（拉格朗日基多项式）。这个唯一的多项式 $F(X_3,X_2,X_1)$ 被称为 向量的多线性扩展（MLE）。
在该例子中，SumCheck 问题定义如下：
$∑Xi∈{0,1}F(X3,X2,X1)=?C,C∈F.\sum_{X_i\in \{0,1\}} F(X_3,X_2,X_1) \stackrel{?}{=} C, \quad C \in \mathbb{F}.$

该协议的流程如下：在每一轮中，证明者计算并承诺一个单变量（线性）多项式，并接收来自验证者的随机挑战。

轮次	证明者 $P\mathcal{P}$	通信	验证者 $V\mathcal{V}$
1	$r1(X):=∑X2,3∈{0,1}F(X3,X2,X)r_1(X) := \sum_{X_{2,3}\in \{0,1\}} F(X_3, X_2,X)$	$r1(X)⟶⟵α1∈Fr_1(X)\longrightarrow\\\longleftarrow \alpha_1\in \mathbb{F}$	$C=?∑X∈{0,1}r1(X)C\stackrel{?}{=} \sum_{X\in\{0,1\}} r_1(X)$
2	$r2(X):=∑X3∈{0,1}F(X3,X,α1)r_2(X) := \sum_{X_3\in \{0,1\}} F(X_3, X,\alpha_1)$	$r2(X)⟶⟵α2∈Fr_2(X)\longrightarrow\\\longleftarrow \alpha_2\in \mathbb{F}$	$r1(α1)=?∑X∈{0,1}r2(X)r_1(\alpha_1)\stackrel{?}{=} \sum_{X\in\{0,1\}} r_2(X)$
3	$r3(X):=F(X,α2,α1)r_3(X) := F(X, \alpha_2,\alpha_1)$	$r3(X)⟶r_3(X)\longrightarrow$	$r2(α2)=?∑X∈{0,1}r3(X)r3(α3)=?F(α3,α2,α1)r_2(\alpha_2)\stackrel{?}{=} \sum_{X\in\{0,1\}} r_3(X)\\r_3(\alpha_3)\stackrel{?}{=} F(\alpha_3,\alpha_2,\alpha_1)$

在此希望估计证明者在每轮计算这些多项式时的复杂度。注意，证明者承诺每个线性单变量多项式的过程并不是计算瓶颈，因为它只涉及简单的椭圆曲线加法或一个小规模的 MSM。

经过简单计算可得，第 1 轮后的多项式形式为：
$r1(X)=∑Xi∈{0,1}F(X2,X2,X)=∑i=03r1(i)(X),r1(i)(X)=f2i(1−X)+f2i+1Xr_1(X) = \sum_{X_i \in \{0,1\}} F(X_2,X_2,X) = \sum_{i=0}^3 r_1^{(i)}(X), \quad r_1^{(i)}(X) = f_{2i}(1-X) + f_{2i+1}X$

显然：
$∑X∈{0,1}r1(X)=r1(0)+r1(1)=∑i=03(f2i+f2i+1)=C\sum_{X \in \{0,1\}} r_1(X) = r_1(0) + r_1(1) = \sum_{i=0}^3 (f_{2i} + f_{2i+1}) = C$

设第 1 轮的挑战为 $α1∈Fp\alpha_1 \in \mathbb{F}_p$ 。那么第 2 轮的多项式为：
$r2(X)=∑Xi∈{0,1}F(X2,X,α1)=∑i=01r2(i)(X),r2(i)(X)=r1(2i)(α1)(1−X)+r1(2i+1)(α1)Xr_2(X) = \sum_{X_i \in \{0,1\}} F(X_2,X,\alpha_1) = \sum_{i=0}^1 r_2^{(i)}(X), \quad r_2^{(i)}(X) = r_1^{(2i)}(\alpha_1)(1-X) + r_1^{(2i+1)}(\alpha_1)X$

类似地，设第 2 轮的挑战为 $α2∈Fp\alpha_2 \in \mathbb{F}_p$ 。则第 3 轮的多项式为：
$r3(X)=F(X,α2,α1)=r2(0)(α2)(1−X)+r2(1)(α2)Xr_3(X) = F(X,\alpha_2,\alpha_1) = r_2^{(0)}(\alpha_2)(1-X) + r_2^{(1)}(\alpha_2)X$

证明者的算法可以用下图表示：
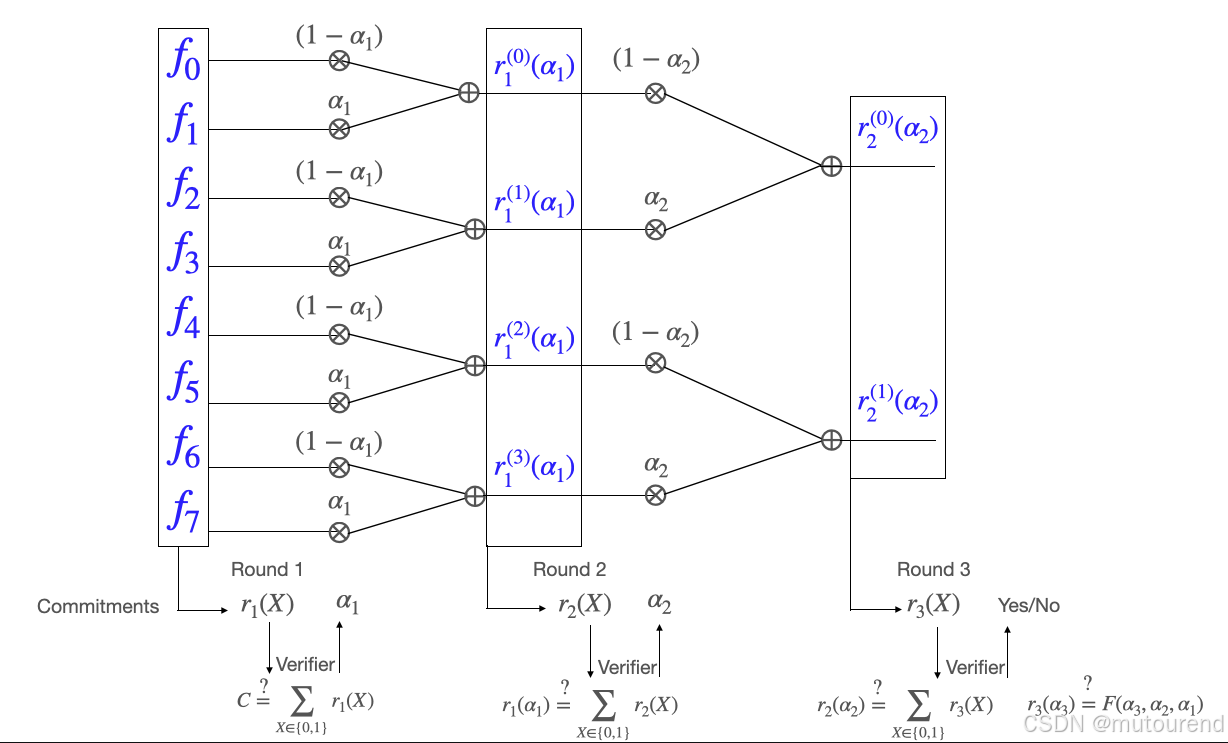
在这里插入图片描述

证明者的复杂度总结如下表（记号 $xFx\mathbb{F}$ 表示内存中存有 $x$ 个有限域元素）：

轮次	操作	内存	乘法数	加法数
预处理	存储 $fi,∀i=0,1,…,7f_i, \forall i=0,1,\dots,7$	$8F8\mathbb{F}$	-	-
1	读取 $fi,∀i=0,1,…,7f_i, \forall i=0,1,\dots,7$ ，承诺 $r_1(X)$ ，接收 $α1\alpha_1$
	读取 $fi,∀i=0,1,…,7f_i, \forall i=0,1,\dots,7$ ，计算 $r1(i)(α1),∀i=0,1,2,3r_1^{(i)}(\alpha_1), \forall i=0,1,2,3$	-	8	4
	清除 $fi,∀i=0,1,…,7f_i, \forall i=0,1,\dots,7$ ，存储 $r1(i)(α1),∀i=0,1,2,3r_1^{(i)}(\alpha_1), \forall i=0,1,2,3$	$4F4\mathbb{F}$	-	-
2	读取 $r1(i)(α1),∀i=0,1,2,3r_1^{(i)}(\alpha_1), \forall i=0,1,2,3$ ，承诺 $r_2(X)$ ，接收 $α2\alpha_2$
	读取 $r1(i)(α1),∀i=0,1,2,3r_1^{(i)}(\alpha_1), \forall i=0,1,2,3$ ，计算 $r2(i)(α2),∀i=0,1r_2^{(i)}(\alpha_2), \forall i=0,1$	-	4	2
	清除 $r1(i)(α1),∀i=0,1,2,3r_1^{(i)}(\alpha_1), \forall i=0,1,2,3$ ，存储 $r2(i)(α2),∀i=0,1r_2^{(i)}(\alpha_2), \forall i=0,1$	$2F2\mathbb{F}$	-	-
3	读取 $r2(i)(α2),∀i=0,1r_2^{(i)}(\alpha_2), \forall i=0,1$ ，承诺 $r_3(X)$
	清除 $r2(i)(α2),∀i=0,1r_2^{(i)}(\alpha_2), \forall i=0,1$

3.2 HyperPlonk 中的 SumCheck 一般形式

该算法的一般形式可以很容易地从上面的简单例子推广出来。考虑一个大小为 $T = 2^n$ 的执行轨迹（为方便起见，假设该执行轨迹总是补零到 2 的幂）。该执行轨迹可以用一个多变量多项式 $F(Xn,…,X1)F(X_n, \ldots, X_1)$ 进行插值。证明者算法如下：

第 1 轮，证明者计算线性多项式：
$r1(i)(X)=(1−X)f2i+Xf2i+1,∀i=0,…,T/2−1r_1^{(i)}(X) = (1-X) f_{2i} + X f_{2i+1}, \quad \forall i=0, \ldots, T/2-1$
并承诺它们的和：
$r1(X)=∑i=0T/2−1r1(i)(X)=∑X∈{0,1}F(Xn,…,X2,X)r_1(X) = \sum_{i=0}^{T/2-1} r_1^{(i)}(X) = \sum_{X \in \{0,1\}} F(X_n, \ldots, X_2, X)$
然后，证明者接收验证者给出的挑战 $α1\alpha_1$ 。
第 $k$ 轮，证明者计算线性多项式：
$rk(i)(X)=(1−X)rk−1(2i)(αk−1)+Xrk−1(2i+1)(αk−1),∀i=0,…,T/2k−1r_k^{(i)}(X) = (1-X) r_{k-1}^{(2i)}(\alpha_{k-1}) + X r_{k-1}^{(2i+1)}(\alpha_{k-1}), \quad \forall i=0, \ldots, T/2^k - 1$
并承诺它们的和：
$rk(X)=∑i=0T/2k−1rk(i)(X)=∑X∈{0,1}F(Xn,…,Xk+1,X,αk−1,…,α1)r_k(X) = \sum_{i=0}^{T/2^k-1} r_k^{(i)}(X) = \sum_{X \in \{0,1\}} F(X_n, \ldots, X_{k+1}, X, \alpha_{k-1}, \ldots, \alpha_1)$
然后，证明者接收验证者给出的挑战 $αk\alpha_k$ 。
最终第 $n$ 轮，证明者计算并承诺线性多项式：
$rn(X)=(1−X)rn−1(0)(αn−1)+Xrn−1(1)(αn−1)r_n(X) = (1-X) r_{n-1}^{(0)}(\alpha_{n-1}) + X r_{n-1}^{(1)}(\alpha_{n-1})$

因此，证明者的总体复杂度为：

$2 T - 4$ 次乘法
$T - 2$ 次加法
以及存储 $T$ 个有限域元素的内存

事实上，可以进一步优化：
$rk(i)(X)=(1−X)rk−1(2i)(αk−1)+Xrk−1(2i+1)(αk−1)=rk−1(2i)(αk−1)+X(rk−1(2i+1)(αk−1)−rk−1(2i)(αk−1))r_k^{(i)}(X) = (1-X) r_{k-1}^{(2i)}(\alpha_{k-1}) + X r_{k-1}^{(2i+1)}(\alpha_{k-1}) = r_{k-1}^{(2i)}(\alpha_{k-1}) + X \big(r_{k-1}^{(2i+1)}(\alpha_{k-1}) - r_{k-1}^{(2i)}(\alpha_{k-1})\big)$

这样可以将所需的乘法次数减半。

更一般地来说：
Sumcheck 协议通常用于证明一个关于多项式在多维域上求和的断言（通常是布尔超立方体 ${0,1\}^d$ ）。换句话说，证明者希望让验证者相信：

给定多项式 $P(x_1, x_2, …, x_d)$ ，在所有变量取值的情况下，其求和结果等于某个特定值 $C$ 。

形式化表示为：
$∑x1,x2,…,xd∈FP(x1,x2,…,xd)=C\sum_{x_1,x_2,\ldots,x_d \in \mathbb{F}} P(x_1, x_2, \ldots, x_d) = C$

Sumcheck 协议是一个迭代过程，每一轮（iteration）包含两个主要计算：

1）累积当前轮次的多项式；
2）通过“折叠（folding）”多项式，使元素数量减少一半。

在每一轮中，验证者会生成挑战值，用来折叠多项式。

4. 引入 Fiat-Shamir

Fiat-Shamir 变换可以将交互式的public coin proof（如 SumCheck 协议）转换为非交互式证明。
在该变换中，挑战 $αi\alpha_i$ 并不是由验证者发送，而是在每一轮通过计算前一轮协议的通信记录（transcript）的哈希函数来生成。

为了避免安全漏洞，每个哈希函数的输入必须包含前一轮的所有可验证结果。相关的漏洞分析见：

2022年4月博客 Coordinated disclosure of vulnerabilities affecting Girault, Bulletproofs, and PlonK
和更技术化的说明见2016年论文 How not to Prove Yourself: Pitfalls of the Fiat-Shamir Heuristic and Applications to Helios。

因此，在 SumCheck 协议中，每一轮必须 顺序执行，而不能并行化跨轮次的计算。正如下文所示，这一事实严重限制了在 HyperPlonk 中进行并行计算的能力。

5. 硬件中的 SumCheck

基于上文对非交互式 SumCheck 的介绍，可以总结出每一轮 $i$ 的操作模式如下：

（从内存中）读取 $2^i$ 个元素
计算 $ai=hash(transcript)a_i = \text{hash(transcript)}$
计算新的 $2^{i-1}$ 个元素
写入 $2^{i-1}$ 个元素（到内存中）

具体来说，假设有 $2^{30}$ 个有限域元素。为了进入下一轮——得到 $2^{29}$ 个元素，必须使用（从内存中读取）全部的 $2^{30}$ 个元素。在完成这一步之前，不能继续进入再下一轮——即 $2^{28}$ 个元素的阶段。

这种 “硬停顿（hard stop）” 意味着在每一轮中，都必须重新访问内存。举个例子，对于大小 $2^{30}$ 的 SumCheck，必须对内存进行 30 次读写。

对于足够小的规模，如 $2^{18}$ ，这些数据可以存储在 SRAM 中。SRAM 速度很快，几乎不会成为瓶颈。

然而，对于大规模的 SumCheck，如 $2^{30}$ （这也是在实际中预期会遇到的规模），部分轮次必须使用 DRAM（如 DDR 或 HBM）。而 DRAM 的速度很慢，会成为瓶颈，甚至超过 SumCheck 计算本身的开销。

下图展示了这种 SumCheck 的数据流：
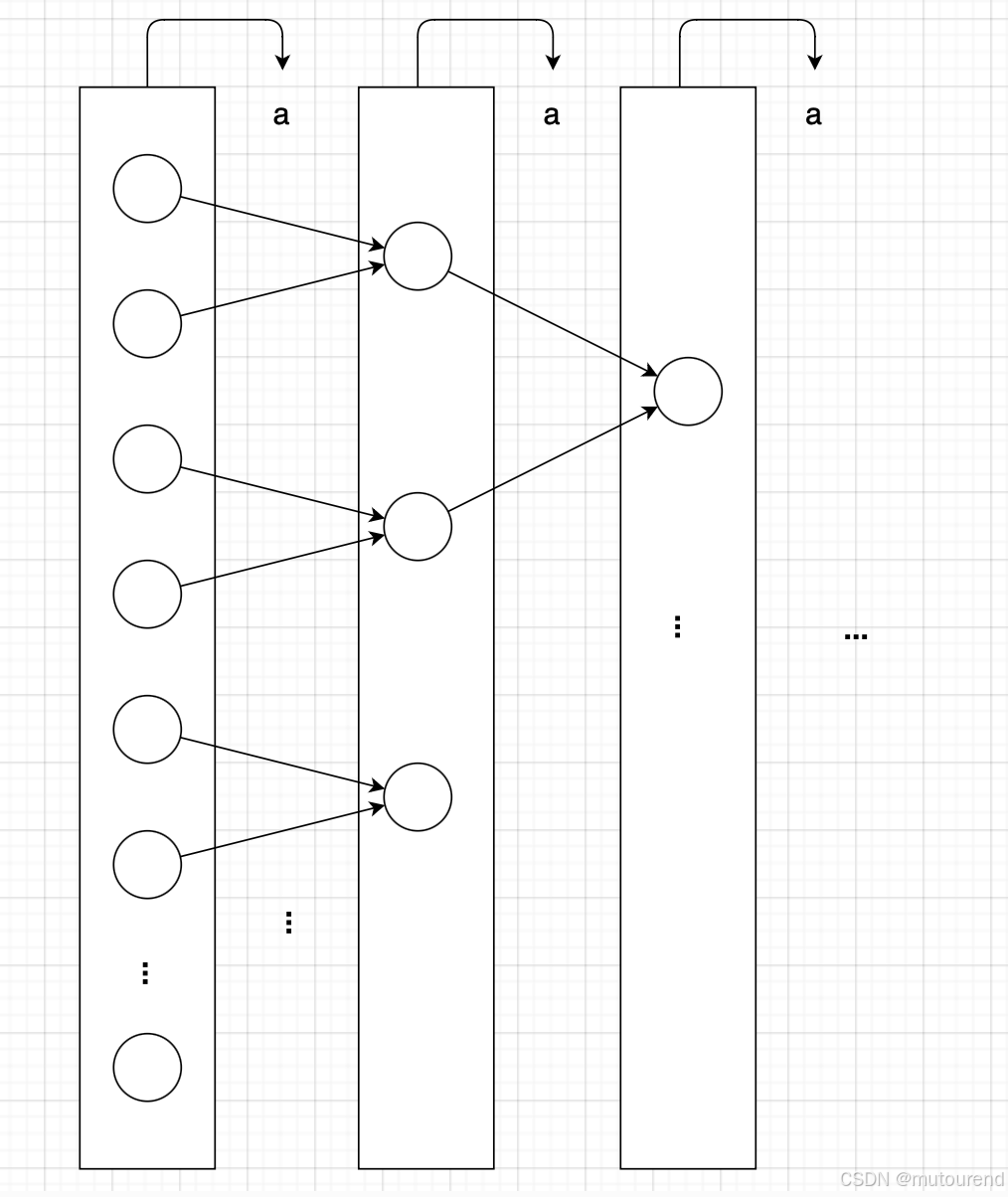
在这里插入图片描述

类似这样的 内存瓶颈 正是在设计硬件加速器时通常希望避免的，因为这类计算几乎没有办法通过硬件加速来优化。由于其本质，标准的 SumCheck 轮次结构极度 串行化，因此几乎没有并行加速的空间。

5.1 硬件中的 NTT

最明显的对比就是 NTT 在硬件中的实现方式。本文不会像讨论 SumCheck 那样深入分析 NTT。为了对比，给出以下示意图：
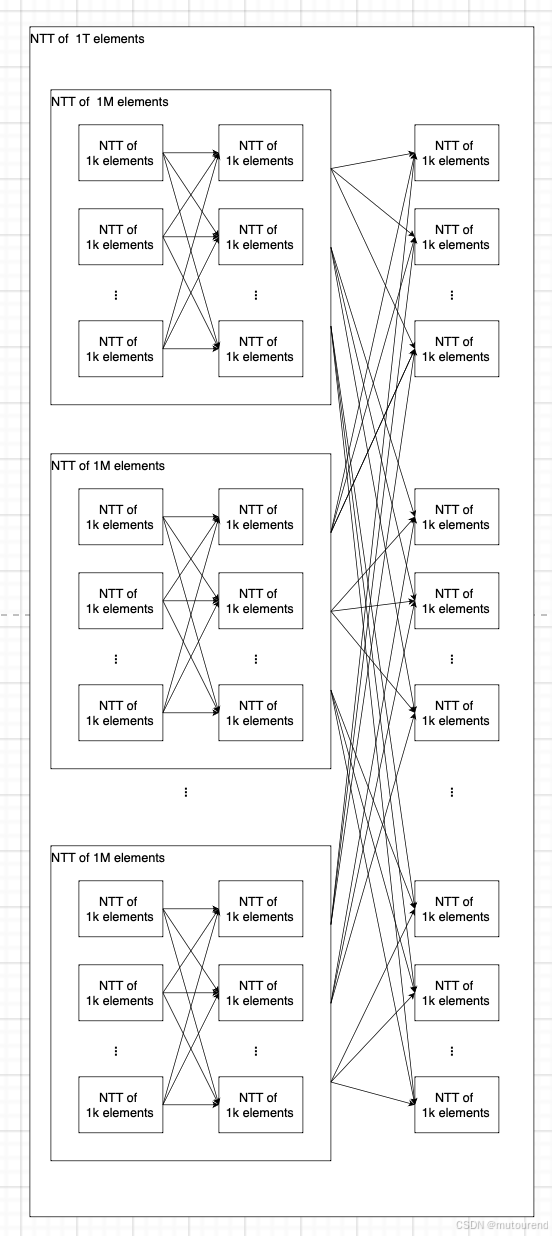
在这里插入图片描述

NTT 天然具有较强的 并行性，因此多个轮次可以在 不返回内存 的情况下连续进行。注意：

在 NTT 中，由于没有 Fiat-Shamir 变换的约束，因此不存在 硬停顿（hard stop） —— 一轮计算的输出（部分结果）可以直接作为下一轮计算的输入（部分输入）。

经验法则是：

可以在 仅一次内存访问 的情况下完成一个规模为 $1 k$ 个元素的完整 NTT。这比 SumCheck 快 10 倍！

如：甚至可以用 仅 3 次内存读写（读取并写回所有元素）完成一个 规模为 1 万亿 个元素的 NTT。

这使得 NTT 是计算受限（compute-bound）的，而不是 内存受限（memory-bound）的。

事实上，Ingonyama团队在 GPU 和 FPGA 上的 NTT 实现已经将计算速度提升到这样一个程度：

在所有相关规模下，计算本身都不再是瓶颈！

这些实现所面临的下一个瓶颈是 PCIe 带宽，也就是与主机进行通信时的传输速度。

5.2 Ingonyama团队 ICICLE 中的 Sumcheck

Ingonyama团队在 CPU 和 GPU（CUDA 和 Metal）上的 Sumcheck 实现，首次在 ICICLE V3.5 中引入，利用 Fiat-Shamir 启发式将协议转化为非交互形式，从而消除了基于轮次的通信需求。

除了支持一组固定的运算外，这些实现还允许通过一种称为 Program 类的高级抽象来定义多线性多项式的用户自定义积。该类使开发者能够在向量上定义自定义逐元素的 lambda 函数，然后将其编译为针对目标硬件优化的后端代码。ICICLE V3.5 随附了内置程序，如：

$A (X) * B (X) - C (X)$
$eq(X)∗(A(X)∗B(X)−C(X))\text{eq}(X) * (A(X) * B(X) - C(X))$

同时仍然保留了指定更复杂约束的完全灵活性。系统设计时注重硬件无关的优化，利用 CPU 的多线程和 GPU 的并行性来最小化内存开销并最大化算术吞吐量。这些改进是 ICICLE 为使密码学原语在不同架构上既可移植又高效的更广泛努力的一部分。

CUDA 实现的计算轮次结构略有不同。在每一轮中，它同时计算上一轮的折叠结果和当前轮的多项式评估，从而消除了不必要的内存访问。值得注意的是，在第一轮中，仅进行多项式评估而不执行折叠。这种设计带来了目前所知最节省内存的实现方式，仅执行折叠严格所需的内存操作。

Fiat-Shamir 挑战和多项式累积直接在设备上计算，无需在每一轮后将数据传回主机再传回设备。这避免了昂贵的往返数据传输，提高了整体吞吐量。

Ingonyama团队将使用该实现来验证此前提出的观点：

Sumcheck 是 受限于内存而非计算能力。

5.2.1 Sumcheck 的限制因素

Ingonyama团队使用 NVIDIA Nsight Compute 对 ICICLE 的 CUDA 实现进行性能剖析，并在 NVIDIA L4 GPU 上识别性能瓶颈。该剖析工具为每个 CUDA 内核提供详细的指标，包括运行时间、内存带宽和寄存器使用情况。为了确定协议的限制因素，Ingonyama团队重点关注内存和计算的 SoL（Speed of Light）吞吐量指标。SoL 指标反映某个子单元的运行接近理论最大吞吐量的程度，有助于判断瓶颈是由内存访问还是计算引起的。

在此次实验中，使用了 4 个大小为 $2^{25}$ 的多项式（即 HyperPlonk 使用的规模范围），并采用组合函数 EQ(AB-C)（R1CS zero check）。

下图展示了 ICICLE Sumcheck 实现的主要 CUDA 内核在协议前 13 轮中的计算和内存 SoL 吞吐量，揭示了执行过程中的性能趋势。
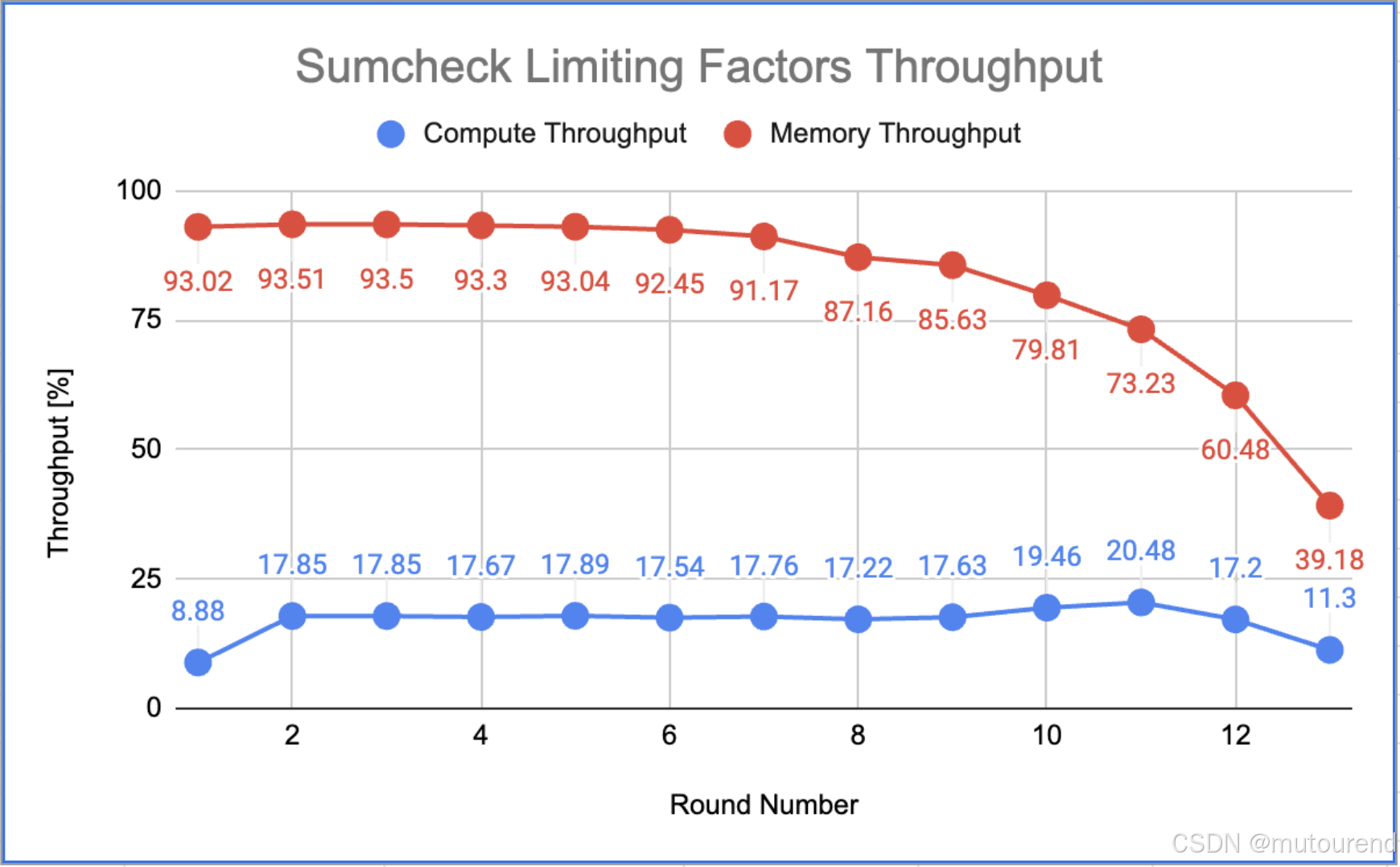
在这里插入图片描述

数据揭示了内存与计算吞吐量在初始阶段的关系：

内存 SoL 吞吐量接近峰值，而计算 SoL 吞吐量相对较低。

当一个程序的内存吞吐受限，导致计算资源无法得到充分利用时，它就被认为是 内存受限（memory-bound）。从图表可见，内存接近满负荷运行，而计算资源未被充分利用，明显表明存在内存瓶颈。

随着轮次推进，出现了一个关键模式：

内存吞吐逐渐下降，而计算吞吐保持稳定甚至略有上升。

第一次到第二次轮次间计算吞吐的翻倍源于协议结构的特性。值得注意的是，只有当内存吞吐下降到 60% 以下时，计算吞吐才开始下降，这进一步强化了“内存是主要限制因素”的结论。下图对此进行了说明：
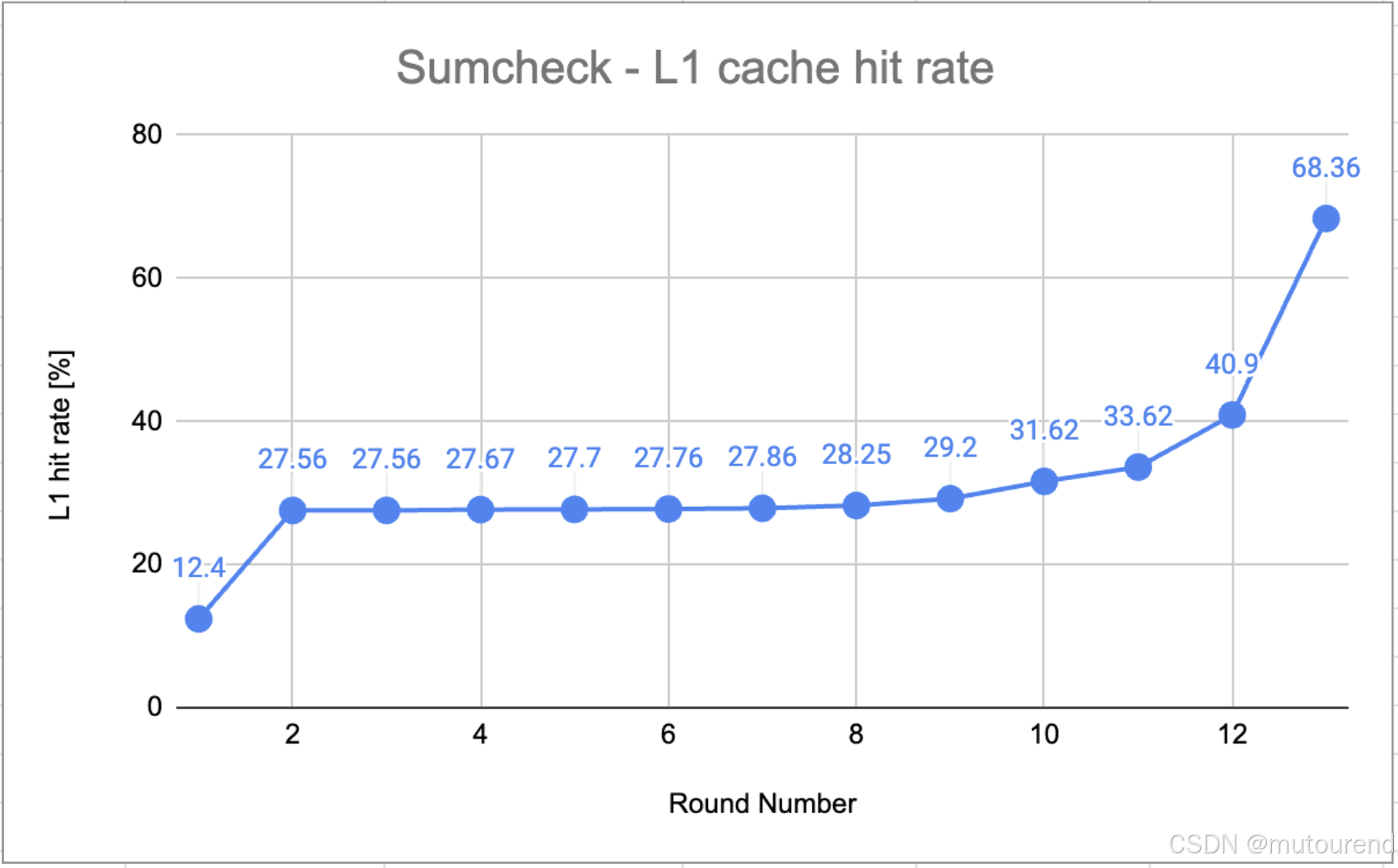
在这里插入图片描述

L1 缓存命中率随着内存吞吐量的下降而上升。

随着轮次推进，多项式规模缩小并逐渐能被缓存容纳，缓存命中率上升。这样一来，更多数据可以直接从缓存中访问，而不必从较慢的主存中获取，从而降低了内存吞吐。同时，计算吞吐因更快的数据访问而提升。

计算利用率因更快的内存访问而提高，这是程序 内存受限 的有力证据。

证据明确表明，内存访问是系统的主要瓶颈。这一点得到了 持续较高的内存 SoL 吞吐量 和 较低的计算利用率 的支持，同时计算吞吐量和 L1 缓存命中率的表现也进一步印证了这一点：随着轮次推进，内存利用率下降，计算性能却有所提高——这进一步强化了工作负载是 内存受限 的结论。

换言之，系统的整体性能是 由内存访问速度 限制的，而非由计算吞吐量所限制。

6. 结论

那么问题来了 —— 是继续使用 Plonk + NTT 更好，还是采用 HyperPlonk + MLE-SumCheck 更好？

至少从 硬件角度 来看，尽管 NTT 本身并没有非常强的并行性，但它依然比 MLE-SumCheck 更加 硬件友好。Ingonyama团队注意到，相同的结构也出现在 FRI 中，如可以参考 plonky2 中的 FRI 实现https://github.com/0xPolygonZero/plonky2/blob/769175808448cecc7b431d7293e2d689af635a4b/plonky2/src/fri/prover.rs#L69。

Ingonyama团队推测，之前之所以没有太多人讨论 FRI 的硬件加速问题，是因为在现有系统（如 STARKs）中，FRI 的开销只占总体计算的一小部分，尤其是与大量、规模更大的 NTT 相比时。

Ingonyama团队实证结果表明，Sumcheck 协议本质上是内存受限的——其性能更多受到内存访问速度的制约，而非计算能力。

因此，优化工作应聚焦于提升内存效率，而不是单纯提高计算性能。

针对内存优化，即使在计算资源有限的硬件上，也能为 Sumcheck 的实现带来显著的性能提升。

另外一个思考在于：

是否已经到了这样一个阶段 —— 零知识证明协议必须结合硬件来共同设计？

参考资料

[1] Ingonyama团队2025年4月1日博客 Hardware-friendliness of HyperPlonk, Part2
[2] Ingonyama团队2022年12月28日hackmd Hardware-friendliness of HyperPlonk
[3] Ingonyama团队2025年4月1日hackmd Hardware-friendliness of HyperPlonk, Part2

查看全文

http://www.dtcms.com/a/359038.html