2023年12月GESP5级C++真题解析，包括选择判断和编程

一、选择题（每道题2分，共30分）

1、下面C++代码用于求斐波那契数列，该数列第1 、2项为1，以后各项均是 前两项之和。下面有关说法错误的是( )

A. fiboA( ) ⽤递归⽅式，fiboB() 循环⽅式

B. fiboA( ) 更加符合斐波那契数列的数学定义，直观易于理解，⽽fiboB() 需 要将数学定义转换为计算机程序实现

C. fiboA( ) 不仅仅更加符合数学定义，直观易于理解，且因代码量较少执⾏ 效率更⾼

D. fiboB( ) 虽然代码量有所增加，但其执⾏效率更⾼

答案：C

解析：A错误，因为fiboA在函数内部自己调用自己是递归，fiboB没有递归还写了for循环，是循环，说法正确，但要选的是错误的。

B错误，因为fiboA确实容易理解，fiboB体现了递推的思想，需要一定计算机基础的人才能看懂。

C正确，fiboA因为没有使用桶记录每个fiboA(i)的值，导致时间复杂度为O(2^n)，而fiboB只需要O(n)的时间，fiboA更慢，说法错误，题目要选错误的，故选C。

D错误，根据对C选项的分析，fiboB更快，该说法正确，不能选。

2、下⾯C++代码以递归⽅式实现合并排序 ，并假设 merge(intT[],intR[],ints,int m, int t) 函数将有序（同样排序规则） 的T[s..m]和T[m+1..t]归并到R[s..t]中 。 横线处应填上代码是( )。

A. mergeSort(SList, T2, s, m,len), mergeSort(SList, T2, m,t,len)

B. mergeSort(SList, T2, s, m-1,len), mergeSort(SList, T2, m+1,t,len)

C. mergeSort(SList, T2, s, m,len), mergeSort(SList, T2, m+1,t,len)

D. mergeSort(SList, T2, s, m-1,len), mergeSort(SList, T2, m-1,t,len)

答案：C

解析：很明显这是一个归并排序的左闭右闭写法(每个区间都包含左端点和右端点)，因此要递归排序左边和右边，而中间的m是分界点，左边的最后一个元素是他，右边的第一个元素的上一个是他，因此左边要写 mergeSort(SList,T2,s,m,len)，即s~m，右边要写mergeSort(SList,T2,m+1,t,len);即m+1~t，故选C。

3、阅读下⾯的C++代码 ，执⾏后其输出是()

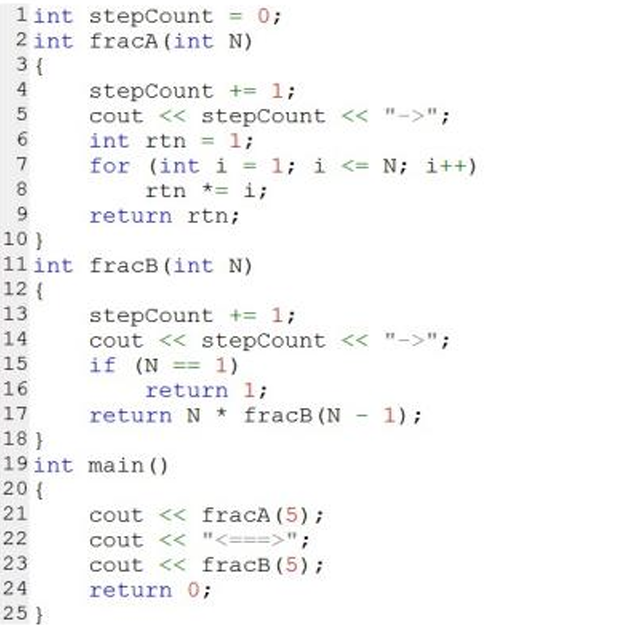
A. 1->120<===>2->120

B. 1->120<===>1->120

C. 1->120<===>1->2->3->4->5->120

D. 1->120<===>2->3->4->5->6->120

答案：D

解析：fracA通过循环求阶乘(1~n的乘积叫n的阶乘)，stepCount只会增加1次，因此先输出1->，然后输出结果120，接着是分隔符。

22行结束后输出：1->120<===>

现在fracB通过递归求阶乘，stepCount没有初始化，因此还是1，从1开始，每调用一次就+1并输出，而fracB(5)会调用5次，所以输出2->3->4->5->6->，最后结果120

最终输出：1->120<===>2->3->4->5->6->120，选D

4、下⾯的C++⽤于对lstA 排序，使得偶数在前奇数在后 ，横线处应填⼊( )。

A. isEven(lstA[j]) && !isEven(lstA[j+1])

B. !isEven(lstA[j]) && isEven(lstA[j+1])

C. lstA[j] > lstA[j+1]

D. lstA[j] < lstA[j+1]

好你个GESP，居然把我选项顺序写反了！我说怎么感觉官方答案不对劲！居然解析都写反了！PDF不可信

（PDF链接）https://gesp.ccf.org.cn/101/attach/1594750635343904.pdf

A. !isEven(lstA[j]) && isEven(lstA[j+1])

B. isEven(lstA[j]) && !isEven(lstA[j+1])

C. lstA[j] > lstA[j+1]

D. lstA[j] < lstA[j+1]

答案：A

解析：这是冒泡排序，交换原则是前后顺序不对就交换。

要求前偶后奇，那么出现前奇后偶的情况就交换。

!isEven(lstA[j])表示前面是奇数，isEven(lstA[j+1])表示后面是偶数，所以应填!isEven(lstA[j]) && isEven(lstA[j+1])，故选A。

5、下⾯的C++代码⽤于将字符串保存到带头节点的双向链表中，并对重复的串 计数，然后将最新访问的串的节点放在链头便于查找。横线处应填⼊代码是（ ）

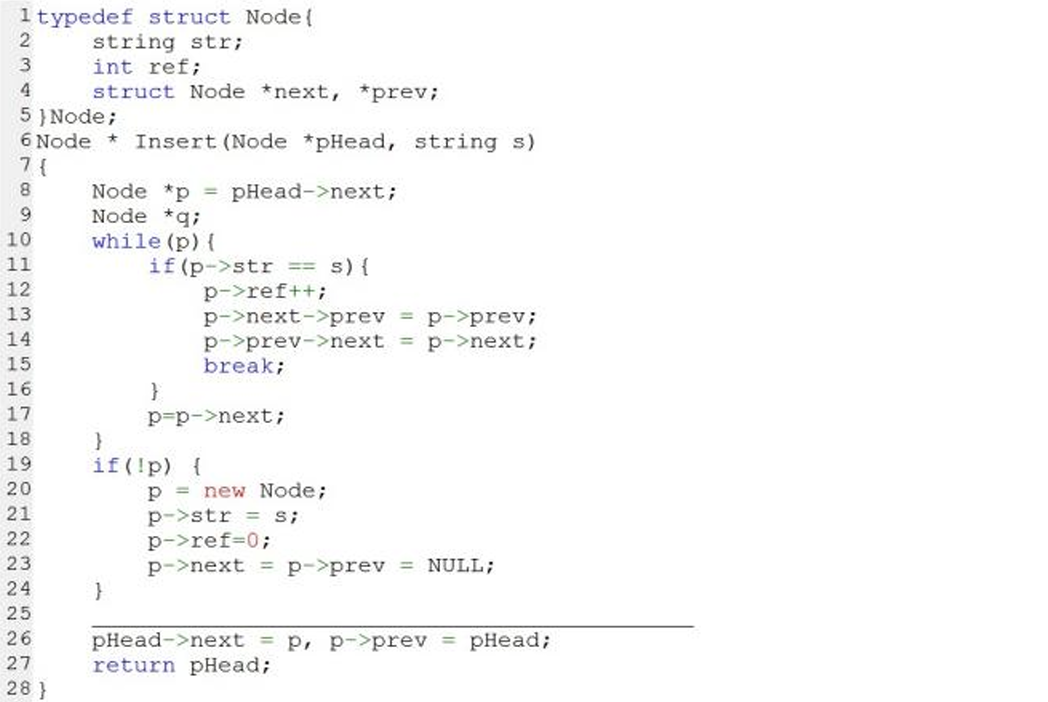
A. if(pHead) {p->next = pHead->next, pHead->next->prev = p;}

B. if(pHead->next) {p->next = pHead->next, pHead->next->prev = p;}

C. p->next =pHead->next, pHead->next->prev = p;

D. 触发异常 ，不能对空指针进⾏操作。

答案：B

解析：都把元素插到链表头部了，那真正头节点不就是pHead->next了吗，此时只需判断pHead->next是否为空就行了，这时候才能插入，因此选B。

6、有关下⾯C++代码说法正确的是（ ）。

A. 如果 x ⼩于10， rc 值也不会超过20

B. foo 可能⽆限递归

C. foo 可以求出 x 和 y 的最⼤公共质因⼦

D. foo 能够求出 x 和 y 的最⼩公倍数

答案：A

解析：本C++代码用辗转相除法求最大公因数

A是正确的，x<10时最大为9，此时y如果<10，则rc不可能超过20，如果y>=10，就会让x和y的位置对调，在递归一次，x回到原来的位置上了，y因为取模x导致<x，这下rc不可能超过20了。

B错误，foo不可能无限递归，即便y为负数。

C错误，辗转相除法求的是最大公因数。

D错误，辗转相除法求的是最大公因数。

故选A。

7、下⾯的C++代码实现对list的快速排序 ，有关说法 ，错误的是（ ）。

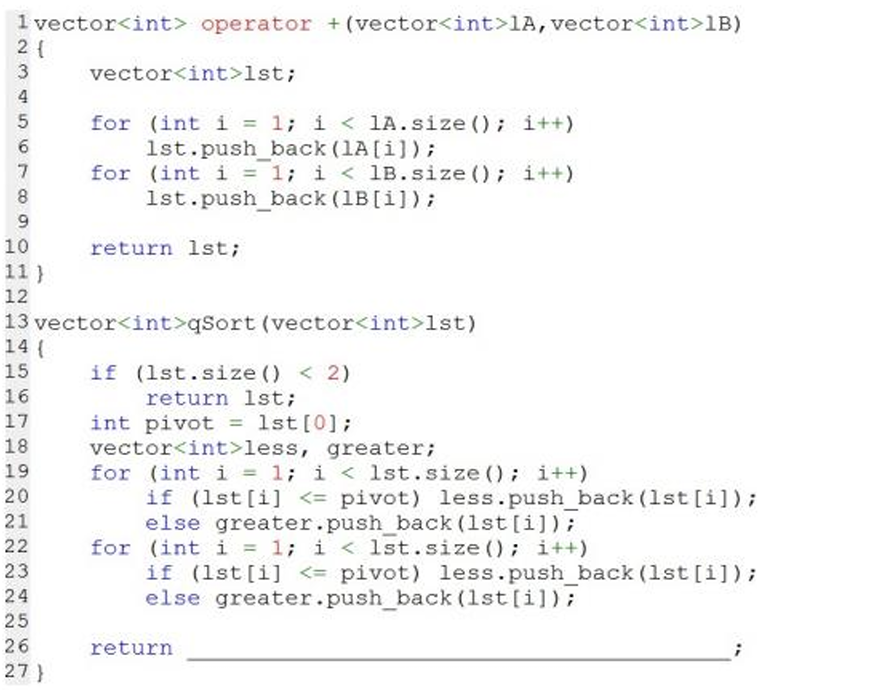
好家伙，这小代码打的，19~21行能打两次，真服了。

A. qSort(less) + qSort(greater) + (vector)pivot

B. (vector)pivot + (qSort(less) + qSort(greater))

C. (qSort(less) + (vector)pivot + qSort(greater))

D. qSort(less) + pivot + qSort(greater)

答案：C

解析：本代码对vector类进行了运算符重载，+号的意义是合并两个vector，快速排序的思想是通过基准将数组分成两部分，一半比基准小(相等)，一半严格比基准大，递归两部分，本代码把小于等于和大于基准的两部分设好了less和greater数组，最后就是返回qsort(less)+vector(pivot)+qsort(greater)，代表递归左边的结果、中间元素、递归右边的结果合并后的数组，代表排序结果，故选C。

8、下⾯C++代码中的 isPrimeA() 和 isPrimeB() 都⽤于判断参数N是否素数 ， 有关其时间复杂度的正确说 法是（ ）。

A. isPrimeA( ) 的最坏时间复杂度是 0（n/2），isPrimeB( ) 的最坏时间复杂度是 O(logN)，isPrimeA() 优于 isPrimeB()

B. isPrimeA() 的最坏时间复杂度是0（n/2 ），isPrimeB( ) 的最坏时间复杂度是 O(N^1/2 )，isPrimeB() 绝⼤多数情况下优于 isPrimeA()

C. isPrimeA() 的最坏时间复杂度是0(N^1/2)，isPrimeB( ) 的最坏时间复杂度是 O(N)，isPrimeA( ) 优于 isPrimeB( ) 

D. isPrimeA() 的最坏时间复杂度是0(logN) ，isPrimeB() 的最坏时间复杂度 是O(N)，isPrimeA() 优于 isPrimeB()

答案：B

解析：O(n/2)是不标准的，但不代表错误，他等价于O(n)。

isPrimeA的时间效率为O(n)，因为i从2加到了n/2，isPrimeB的效率为O(n^1/2)，因为他只枚举了2~根号n。故选B。

9、下⾯C++代码⽤于有序 list 的⼆分查找 ，有关说法错误的是（ ）。

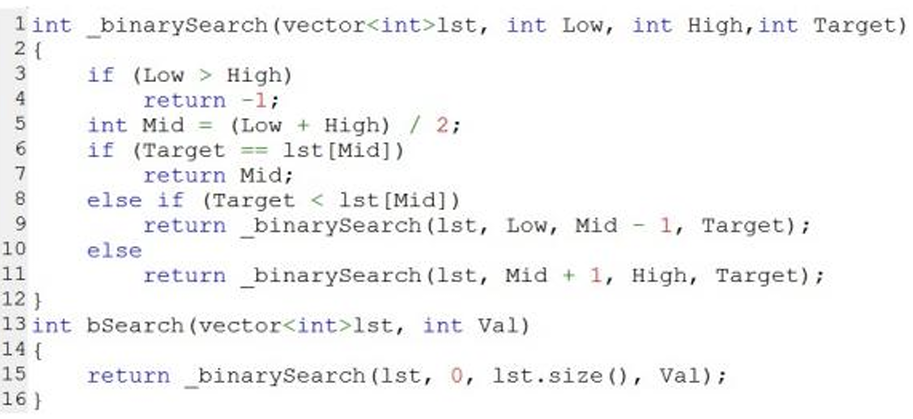
A. 代码采⽤⼆分法实现有序 list 的查找

B. 代码采⽤分治算法实现有序 list 的查找

C. 代码采⽤递归⽅式实现有序 list 的查找

D. 代码采⽤动态规划算法实现有序 list 的查找

答案：D

解析：A错误，代码确实是二分，但题目要找错误的说法；

B错误，代码确实在分治，只不过每次递归只调用一次自身罢了；

C错误，代码确实在递归，因为函数_binarySearch自己调用了自己；

D正确，该代码与动态规划没有任何关系。

10、在上题的_binarySearch算法中，如果lst中有N个元素，其时间复杂度是（ ）

A. O(N)

B. O(logN)

C. O(NlogN)

D. O(N2)

答案：B

解析：二分查找的时间复杂度是O(logn)

11、下⾯的C++代码使⽤数组模拟整数加法，可以处理超出⼤整数范围的加法运 算。横线处应填⼊代码是 () 。

A. c.push_back(t % 10), t = t % 10;

B. c.push_back(t / 10), t = t % 10;

C. c.push_back(t / 10), t = t / 10;

D. c.push_back(t % 10), t = t / 10;

答案：D

解析：结果数组每次只能加入一个位，因此t（进位+两个数的和）的个位要写在结果上，t的个位要去掉，获取个位的代码是t%10，去掉个位保留十位的代码是t/10，因此横线应填c.push_back(t%10),t=t/10;选D。

12、有关下⾯C++代码的说法正确的是（ ）。

A. 上述代码构成单向链表

B. 上述代码构成双向链表

C. 上述代码构成循环链表

D. 上述代码构成指针链表

答案：B

解析：首先用构造函数创建一个元素10，然后在后面每创建一个元素就将他的前驱指向前面最后一个元素，因此上述代码构成双向链表。

13、通讯卫星在通信⽹络系统中主要起到（） 的作⽤ 。

A. 信息过滤

B. 信号中继

C. 避免攻击

D. 数据加密

答案：B

解析：通信卫星可以转发无线电信号，实现通信地球站间或地球站与航天器间的无线电通信，因此具有信号中继作用。选B。

14、⼩杨想编写⼀个判断任意输⼊的整数N是否为素数的程序 ，下⾯哪个⽅法 不合适？ ( )

A. 埃⽒筛法

B. 线性筛法

C. ⼆分答案

D. 枚举法

答案：C

解析：埃氏筛法和线性筛法可以找出N以内的素数，判断包不包含N即可；枚举法可以枚举<=根号n的数，通过因数关系判断是否质数；二分答案有点多余。

15、下⾯的排序算法都要处理多趟数据 ，哪种排序算法不能保证在下⼀趟处理 时从待处理数据中选出最⼤或最 ⼩的数据？ ( )

A. 选择排序

B. 快速排序

C. 堆排序

D. 冒泡排序

答案：B

解析：选择排序选出最小元素并交换，堆排序选出最大元素放到堆尾，冒泡排序把最大元素冒泡到最后，但快速排序是选出基准，一半大一半小，不能保证选出最大最小，选B

二、判断题（每道题2分，共20分）

1、归并排序的时间复杂度是O（NlogN) 。

答案：正确

解析：归并排序的平均时间复杂度是O(nlogn)，另见：数据结构：排序算法之归并排序Merge Sort-CSDN博客

2、⼩杨在⽣⽇聚会时拿⼀块H*W的巧克⼒招待来的K个⼩朋友，保证每位⼩朋 友⾄少能获得⼀块相同⼤⼩的巧克⼒ 。那么⼩杨想分出来最⼤边长的巧克⼒可 以使⽤⼆分法。

答案：错误

解析：因为考纲中对二分法同时列出了“二分查找”和“二分答案（或二分枚 举）”。

3、以下C++代码能以递归⽅式实现斐波那契数列 ，该数列第1 、2项为1， 以 后各项均是前两项之和 。

答案：错误

解析：哪来的fiboA和fiboB

4、贪⼼算法可以达到局部最优 ，但可能不是全局最优解 。

答案：正确

解析：贪心是一直做当前最好的选择，可以达到局部最优，但在前边影响后边的题目可能不是全局最优

5、⼩杨设计了⼀个拆数程序，它能够将任意的⾮质数⾃然数N转换成若⼲个质 数的乘积，这个程序是可以设计出来的。

答案：正确

解析：唯一分解定理是存在的，因此可以设计出来程序

6、插⼊排序有时⽐快速排序时间复杂度更低 。 ( )

答案：正确

解析：当数组已经有序，插入排序的时间复杂度为O(n)，快速排序的时间复杂度为O(n^2)，此时插入排序比快速排序快，因此正确。

7、下⾯的C++代码能实现⼗进制正整数N转换为⼋进制并输出 。 

答案：错误

解析：rst应该倒序存储才能使最低位靠后

8、对数组 int arr[]={2,6,3,5,4, 8,1,0, 9, 10} 执⾏ sort(arr, arr+10) ，则执⾏后 arr 中的数据调整为 {0,1,2,3,4,5,6,8,9,10} 。

答案：正确

std::sort在无自定义比较函数的情况下是默认从小到大排序的，而区间是包括左，不包括右的，因此sort的范围恰好布满arr，于是就排成了0 1 2 3 4 5 6 8 9(7被我吃了)

9、⼩杨想写⼀个程序来算出正整数N有多少个因数 ，经过思考他写出了⼀个 重复没有超过N/2次的循环就能够算 出来了 。

答案：正确

解析：可以枚举到n的一半因数，因为另一半没有因数啊啊啊！

10、同样的整数序列分别保存在单链表和双向链中 ，这两种链表上的简单冒泡 排序的复杂度相同。

答案：正确

解析：相邻数据交换，时间还是O(1)，因此时间没啥区别

三、编程题（每道题25分，共50分）

1 小杨的幸运数（普及/提高-）

B3929 [GESP202312 五级] 小杨的幸运数 - 洛谷https://www.luogu.com.cn/problem/B3929

题目描述

小杨认为，所有大于等于 a 的完全平方数都是他的超级幸运数。

小杨还认为，所有超级幸运数的倍数都是他的幸运数。自然地，小杨的所有超级幸运数也都是幸运数。

对于一个非幸运数，小杨规定，可以将它一直 +1，直到它变成一个幸运数。我们把这个过程叫做幸运化。例如，如果a=4，那么 4 是最小的幸运数，而 1 不是，但我们可以连续对 1 做 3 次 +1 操作，使其变为 4，所以我们可以说， 1幸运化后的结果是 4。

现在，小杨给出 N 个数，请你首先判断它们是不是幸运数；接着，对于非幸运数，请你将它们幸运化。

输入格式

第一行 2 个正整数 a,N。

接下来 N 行，每行一个正整数 x ，表示需要判断（幸运化）的数。

输出格式

输出 N 行，对于每个给定的 x ，如果它是幸运数，请输出 lucky，否则请输出将其幸运化后的结果。

输入输出样例

输入 #1

2 4 
1 
4 
5 
9

输出 #1

4 
lucky 
8 
lucky

输入 #2

16 11 
1 
2 
4 
8 
16 
32 
64 
128 
256 
512
1024

输出 #2

16 
16 
16 
16 
lucky 
lucky 
lucky 
lucky 
lucky 
lucky 
lucky

说明/提示

样例解释 1

1 虽然是完全平方数，但它小于 a，因此它并不是超级幸运数，也不是幸运数。将其进行 3 次 +1 操作后，最终得到幸运数 4。4 是幸运数，因此直接输出 lucky 。

5 不是幸运数，将其进行 3 次 +1 操作后，最终得到幸运数 8。

9 是幸运数，因此直接输出 lucky 。

数据规模

对于 30% 的测试点，保证 a,x≤100,N≤100。

对于 60% 的测试点，保证 a,x≤106。

对于所有测试点，保证 a≤1,000,000；保证 N≤2×105；保证 1≤x≤1,000,001。

题目大意

任何大于等于a的完全平方数的倍数都叫幸运数，可以是1倍。

对于非幸运数，可以一直+1，直到幸运为止，这叫幸运化。

输入n个数，如果是幸运数则输出lucky，否则输出他幸运化的值。

题目分析

我们可以设一个bool数组lucky，lucky[i]表示i是否为幸运数，是则true，否则false。

接下来输入，对于每个输入的数字x，去检查lucky[x]是否true，如果true，就输出lucky；

反之，用i从x+1开始枚举到1000001(数据最大值)，去检查每个lucky[i]，如果true就输出并break

由于幸运数比较多，所以可以赌一把时间，本人亲测可AC。

解题步骤

1 读入a N并计算lucky[1000002]数组

2 读入每个x并向后寻找幸运数

1 读入aN并计算lucky

读入aN直接cin>>a>>n;就可以了。

然后用i从ceil(sqrt(a))开始，结束条件为i*i<=1000001，每次i++

这样做的目的是枚举从a到1000001的完全平方数，但是时间慢，于是就从平方根开始，这样时间就能大打折扣！

ceil是向上取整，因为要大于等于a，如果不加ceil就是向下取整，那样就不对了！

所以此时i就代表了i*i，一会i的各种操作都要用i*i代替。

我们枚举的是超级幸运数，于是还要通过j(倍数)来获取i*i*j，如果<=1000001，就可以标记为"幸运"

如果大于，直接BREAK!!!

代码：

bool lucky[1000002];
void work(int a)
{for(int i=ceil(sqrt(a));i*i<=1000001;i++){for(int j=1;i*i*j<=1000001;j++){lucky[i*i*j]=1;}}
}

其中work为求lucky的函数

2 读入x并寻找幸运数

这个...我觉得没必要多说了吧，看代码吧~

for(int i=1;i<=n;i++)
{int x;cin>>x;if(lucky[x])cout<<"lucky\n";else{for(int j=x+1;j<=1000001;j++){if(lucky[j]){cout<<j<<endl;break;}}}
}

完整代码

#include<bits/stdc++.h>
using namespace std;
bool lucky[1000002];
void work(int a)
{for(int i=ceil(sqrt(a));i*i<=1000001;i++){for(int j=1;i*i*j<=1000001;j++){lucky[i*i*j]=1;}}
}
int main()
{int a,n;cin>>a>>n;work(a);for(int i=1;i<=n;i++){int x;cin>>x;if(lucky[x])cout<<"lucky\n";else{for(int j=x+1;j<=1000001;j++){if(lucky[j]){cout<<j<<endl;break;}}}}return 0;
}

AC截图

总结

这题不难，稍加分析就能AC，但是代码的长度，我看普及/提高-也值得。

小杨你明天出个倒霉数行不~

2 烹饪问题（普及/提高-）

B3930 [GESP202312 五级] 烹饪问题 - 洛谷https://www.luogu.com.cn/problem/B3930

题目描述

有 N 种食材，编号从 1 至 N，其中第 i 种食材的美味度为 ai​。

不同食材之间的组合可能产生奇妙的化学反应。具体来说，如果两种食材的美味度分别为 x 和 y ，那么它们的契合度为 x and y。

其中，and 运算为按位与运算，需要先将两个运算数转换为二进制，然后在高位补足 ，再逐位进行与运算。例如，12 与 6 的二进制表示分别为 1100 和 0110 ，将它们逐位进行与运算，得到 0100 ，转换为十进制得到 4，因此 12 and 6=4。在 C++ 或 Python 中，可以直接使用 & 运算符表示与运算。

现在，请你找到契合度最高的两种食材，并输出它们的契合度。

输入格式

第一行一个整数 N，表示食材的种数。

接下来一行 N 个用空格隔开的整数，依次为 a1​,⋯,aN​，表示各种食材的美味度。

输出格式

输出一行一个整数，表示最高的契合度。

输入输出样例

输入 #1

3
1 2 3

输出 #1

2

输入 #2

5
5 6 2 10 13

输出 #2

8

说明/提示

样例解释 1

可以编号为 1,2 的食材之间的契合度为 2 and 3=2，是所有食材两两之间最高的契合度。

样例解释 2

可以编号为 3,4 的食材之间的契合度为 10 and 13=8，是所有食材两两之间最高的契合度。

数据范围

对于 40% 的测试点，保证 N≤1,000；

对于所有测试点，保证 N≤10^6，0≤ai​≤2,147,483,647。

TLE做法

有些孩子上来就暴力枚举食材，然后两两求值取最大，代码往往一成不变地长这样：

#include<bits/stdc++.h>
using namespace std;
int a[1000001];
int main()
{int n;cin>>n;for(int i=1;i<=n;i++)cin>>a[i];int mx=0;for(int i=1;i<n;i++){for(int j=i+1;j<=n;j++){mx=max(mx,a[i]&a[j]);}}cout<<mx;return 0;
}

恭喜你！TLE了~别着急，我们来分析一下题目。

题目大意

给定n个正整数，求他们两两组合的最大按位与值。

题目分析

我们可以暴力枚举食材，然后求最大的与值。但是这样会TLE超时，因此我们不妨换个思路：

倒序排序，然后看前32个数进行暴力就行了，时间复杂度...O(nlogn)，因为排序。

接下来看我证明~

众所周知，两个数按位与的最高位最高是两个数中的更低位。

倒序排序，高位就越有可能是1，而数据一共是32位。

前32个数字肯定能覆盖所有位，因为如果位数全不同，那么每个位都覆盖到，如果有相同，就会更完整地覆盖向下的位，注意所有位指的是所有数的最高位，以二进制为准。

OK现在只需要前32个数字，那么这样除了排序外，剩下部分的时间复杂度就是O(n)读入和O(1)计算了。

解题步骤

1 读入数据并排序

2 n的值缩小并暴力

1 读入数据并排序

这个没啥好说的

int n;
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
sort(a+1,a+n+1,greater<int>());

这里的greater<int>()其实是C++标准库提供的自定义比较函数：大于，小于就是less。

大于就是我们想要的相邻元素关系，这就相当于倒序。

2 n的值缩小并暴力

这个没有说的吧~

n=min(n,32);
int mx=0;
for(int i=1;i<n;i++)
{for(int j=i+1;j<=n;j++){mx=max(mx,a[i]&a[j]);}
}
cout<<mx;
return 0;

min和max都是std提供的最小最大函数，用于求两个数之间谁更大谁更小。

完整代码

#include<bits/stdc++.h>
using namespace std;
int a[1000001];
int main()
{int n;cin>>n;for(int i=1;i<=n;i++)cin>>a[i];sort(a+1,a+n+1,greater<int>());n=min(n,32);int mx=0;for(int i=1;i<n;i++){for(int j=i+1;j<=n;j++){mx=max(mx,a[i]&a[j]);}}cout<<mx;return 0;
}

AC截图

总结

这题比较复杂，有点考验数学能力，尤其是前32个数字的证明，完全就是二进制运算的高级用法！

结语

祝各位考生在考场上超常发挥，斩获高分！