吴恩达机器学习作业五：神经网络正向传播

数据集在作业一

正向传播

正向传播（Forward Propagation）是神经网络计算过程中的核心步骤，指的是将输入数据通过神经网络的各层依次传递，最终得到输出结果的过程。

核心原理

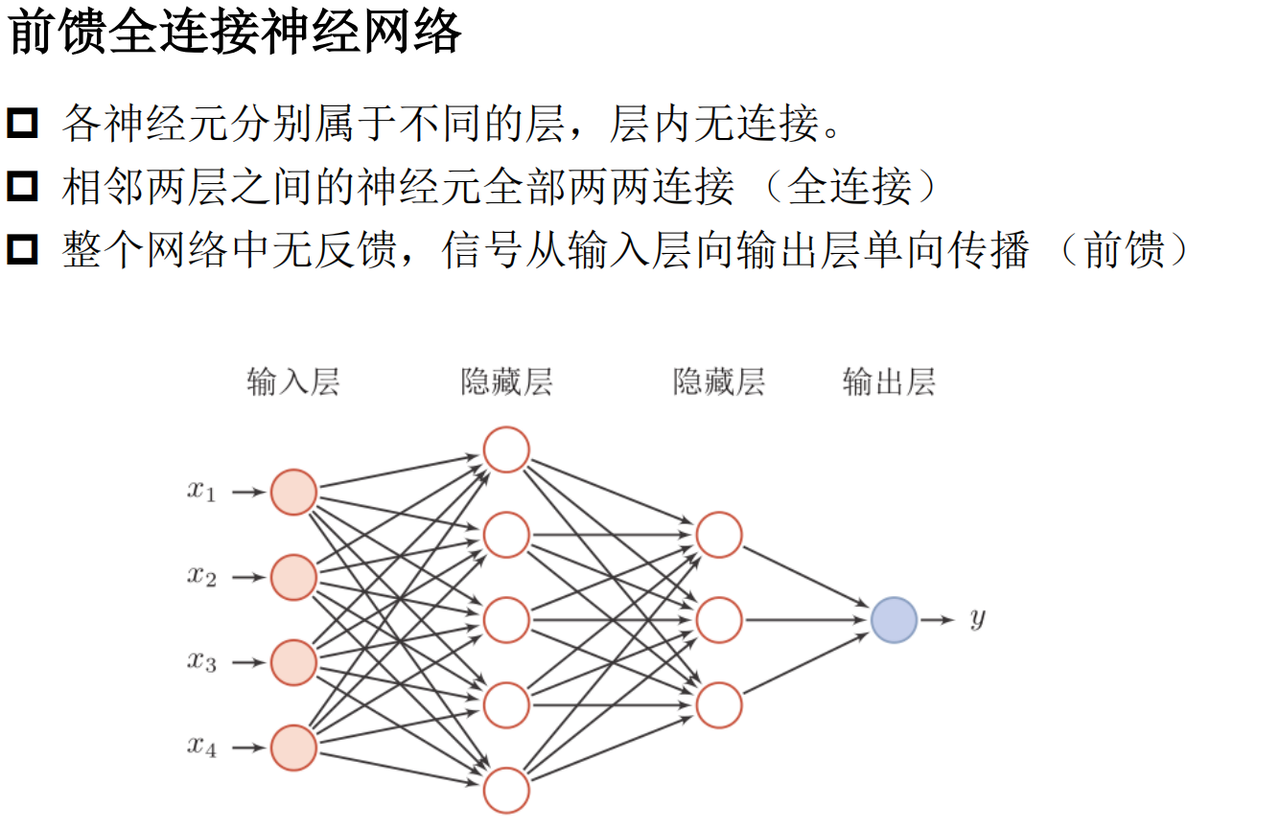
在神经网络中，信息从输入层流入，经过一个或多个隐藏层的处理，最终从输出层流出。每一层的计算都依赖于上一层的输出，具体包括两个步骤：

1. 加权求和：将上一层神经元的输出与当前层的权重进行加权求和，并加上偏置项（bias）。

2. 激活函数处理：将加权求和的结果通过激活函数（如 sigmoid、ReLU 等）进行非线性变换，得到当前层神经元的输出。

我们下面要用正向传播的一个全连接神经网络来实现手写数字识别

前面我们提到了如果是处理非线性关系时，我们可以用高次特征项来进行拟合，但是神经网络（这里是全连接层），我们要使用激活函数，从而达到非线性变换的效果。可以数学推导一下，如果只是多个加权求和叠加，那么从输入到输出也还只是加权求和，无法做到非线性的，所以我们采用了非线性函数（激活函数）

代码

读取数据集

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio
"""使用前馈神经网络来实现手写数字识别"""# 读取数据集
data = sio.loadmat("ex3data1.mat")
X = data['X']
y = data['y']
# 权重
theta=sio.loadmat("ex3weights.mat")
# print(theta.keys())
theta1=theta['Theta1']
theta2=theta['Theta2']
# print(theta1.shape,theta2.shape)(25, 401) (10, 26)
y=y.flatten()

激活函数

def sigmoid(z):return 1/(1+np.exp(-z))

前向传播

def forward_propagate(X,theta1,theta2):m=X.shape[0]a1=np.insert(X,0,1,axis=1)z2=np.dot(a1,theta1.T)a2=sigmoid(z2)a2=np.insert(a2,0,1,axis=1)z3=np.dot(a2,theta2.T)a3=sigmoid(z3)return a3# a3=forward_propagate(X,theta1,theta2)
# print(a3.shape)

这里a1是输入层，z2和a2是隐藏层，在隐藏层和输出层中要先进行加权求和在进行激活函数，z3和a3是输出层（这里是对应数字的各自概率）。

预测

# 预测
def predict(X,theta1,theta2):a3=forward_propagate(X,theta1,theta2)return np.argmax(a3,axis=1)+1y_pred=predict(X,theta1,theta2)accuracy=np.mean(y_pred==y)
print(accuracy)##0.9752

总结

读取数据集——激活函数——构建模型（全连接神经网络）——运行并预测。

这里大家如果没有对应的基础，不知道这些参数是怎么得来的，在下一个作业反向传播中会进行讲解，其实和线性回归，逻辑回归中的参数训练类似。