【动态规划】简单多状态 dp 问题

一、按摩师

题目描述：

思路讲解：

本道题需要我们找出最优预约集合使总时间最长，按摩师不能接受相邻预约，问题可拆解为：对于第 i 个预约，接则前一个必须不接，不接则取前一个接或不接的最大值。以下是具体思路：

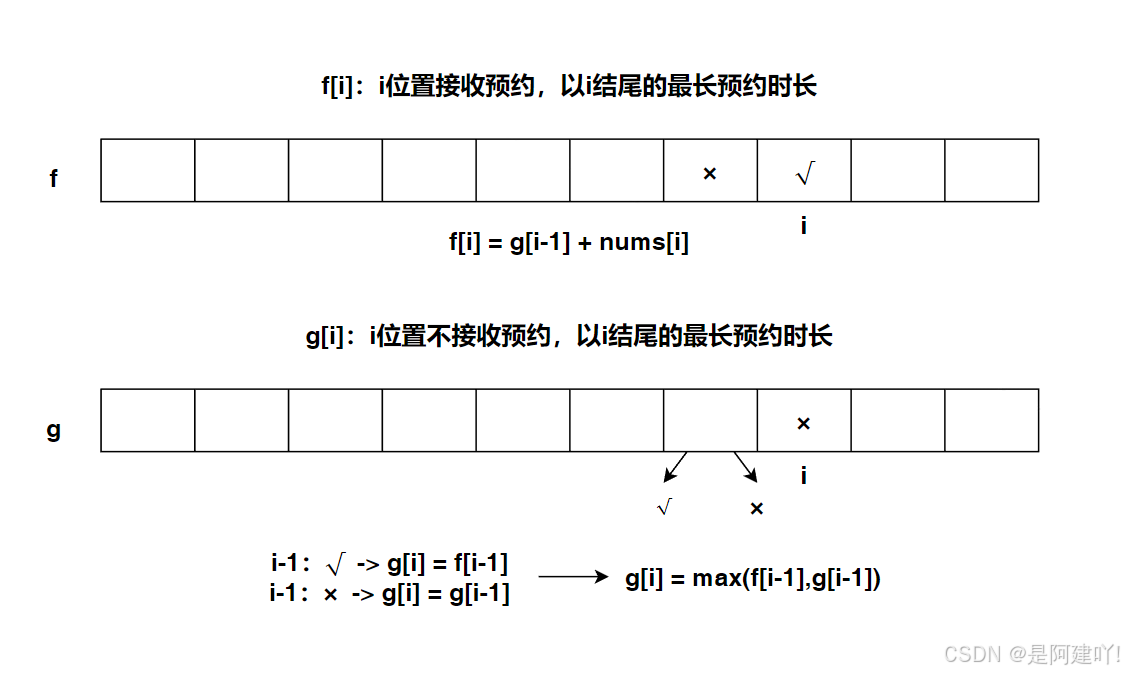
1. 状态表示：
   • f[i] 表示接第 i 个预约时的最长总时间
   • g[i] 表示不接第 i 个预约时的最长总时间
2. 状态转移方程：
   • f[i] = g[i-1] + nums[i]：接第 i 个预约时，前一个必须不接，总时间为前一个不接的最长时间加当前预约时间
   • g[i] = max(g[i-1], f[i-1])：不接第 i 个预约时，总时间为前一个接或不接的最长时间的最大值
3. 初始化：
   • 第 0 个预约：f[0] = nums[0]（接第 0 个预约），g[0] = 0（不接第 0 个预约）
   • 若预约序列为空（n=0），直接返回 0
4. 填写 DP 表：
   • 按照从左到右的顺序，从第 1 个预约遍历到最后一个（i=1 到 i=n-1），基于前一个预约的 f 和 g 值计算当前值
5. 结果返回：
   • 最终结果为最后一个预约接或不接的最长时间的最大值，即 max(f[n-1], g[n-1])

编写代码：

class Solution {
public:int massage(vector<int>& nums) {int n = nums.size();if(n == 0) return 0;vector<int> f(n,0) , g(n,0);f[0] = nums[0];for(int i = 1 ; i < n ; i++){f[i] = g[i-1] + nums[i];g[i] = max(g[i-1],f[i-1]);}return max(f[n-1],g[n-1]);}
};

---

二、打家劫舍 II

题目描述：

思路讲解：
本道题需要我们计算能够偷窃到的最高金额，房屋围成一圈，第一个和最后一个房屋相邻，因此两者不能同时偷窃，问题可拆解为两种互斥场景：要么不偷第一个房屋，要么不偷最后一个房屋，取两种场景的最大值即为结果。以下是具体思路：

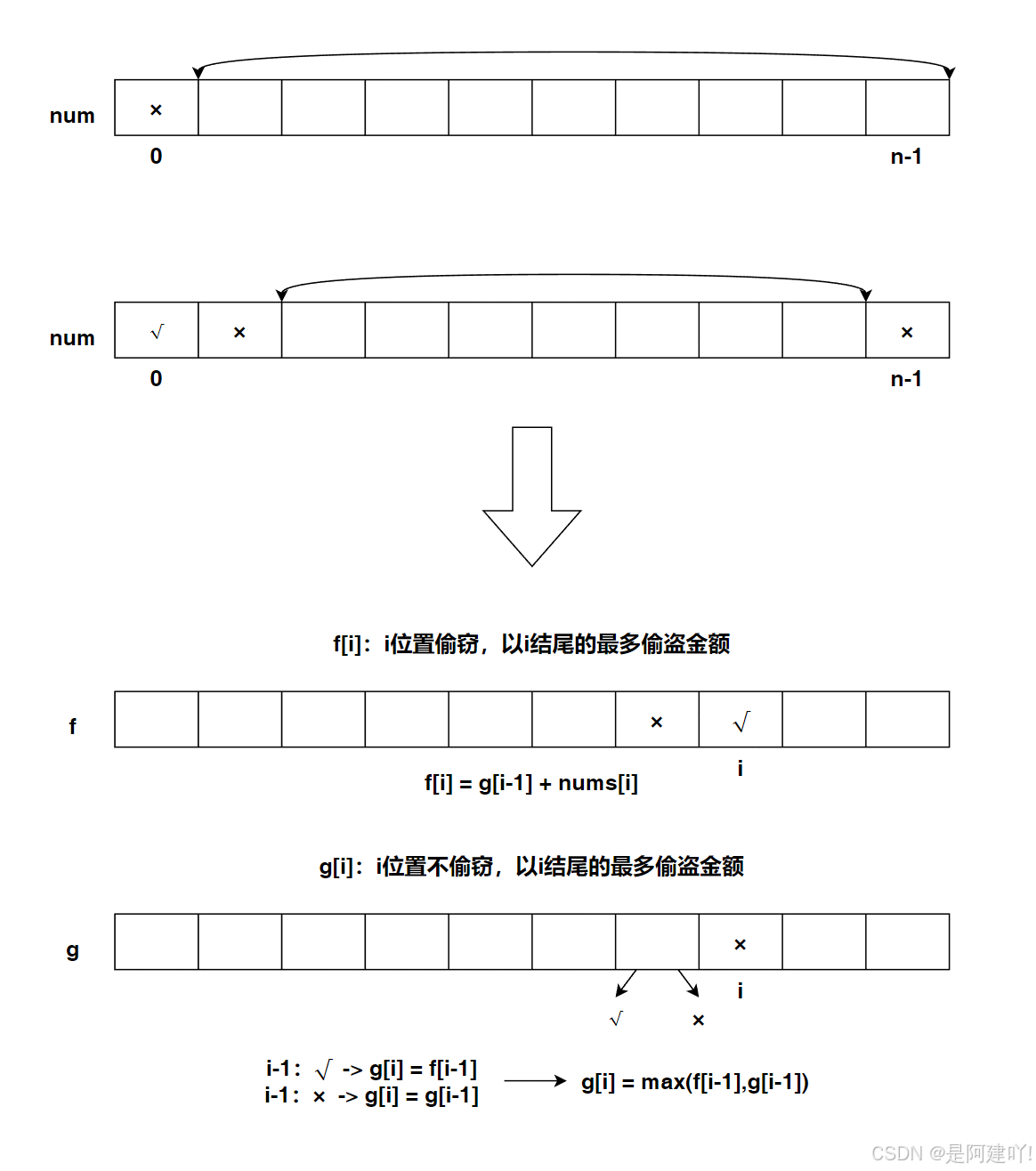
1. 子问题定义与状态设计：
   • 定义辅助函数 rob1(nums, left, right) 计算从第 left 到 right 个房屋（闭区间）的最大偷窃金额，采用双状态数组记录两种情况：
2. 状态表示：
   • f[i] 表示偷窃第 i 个房屋时的最大金额
   • g[i] 表示不偷窃第 i 个房屋时的最大金额
3. 子问题的状态转移方程：
   • f[i] = g[i-1] + nums[i]：偷窃第 i 个房屋时，前一个房屋必须不偷，金额为前一个不偷的最大金额加当前房屋金额
   • g[i] = max(f[i-1], g[i-1])：不偷窃第 i 个房屋时，金额为前一个房屋偷或不偷的最大值
4. 分段处理核心问题：
   • 由于首尾房屋相邻，总问题分为两种场景：
     • 场景 1：偷窃第一个房屋，则最后一个房屋不能偷，需计算 nums[0] + rob1(nums, 2, n-2)（从第 2 个到第 n-2 个房屋的最大金额加第一个房屋金额）
     • 场景 2：不偷窃第一个房屋，则可偷最后一个房屋，需计算 rob1(nums, 1, n-1)（从第 1 个到第 n-1 个房屋的最大金额）
   • 最终结果为两种场景的最大值
5. 边界处理：
   • 若 left > right（区间为空），rob1 直接返回 0
   • 区间起点 left 的初始化：f[left] = nums[left]（偷起点房屋），g[left] = 0（不偷起点房屋）
6. 结果返回：
   • rob1 函数按从 left+1 到 right 的顺序遍历，基于前一个房屋的 f 和 g 值计算当前值，最终返回区间内的最大金额（max(f[right], g[right])）
   • 主函数 rob 返回两种场景的最大值

编写代码：

class Solution {
public:int rob1(vector<int>& nums , int left , int right){int n = nums.size();if(left > right) return 0;vector<int> f(n,0), g(n,0);f[left] = nums[left];for(int i = left + 1 ; i <= right ; i++){f[i] = g[i-1] + nums[i];g[i] = max(f[i-1],g[i-1]);}return max(g[right],f[right]);}int rob(vector<int>& nums) {int n = nums.size();return max(nums[0] + rob1(nums,2,n-2) , rob1(nums,1,n-1));}
};

---

三、删除并获得点数

题目描述：

思路讲解：
本道题需要我们通过操作获得的最大点数，但是按照这个思路并不好直接做，所以可以转变一下思路，以下是具体思路：

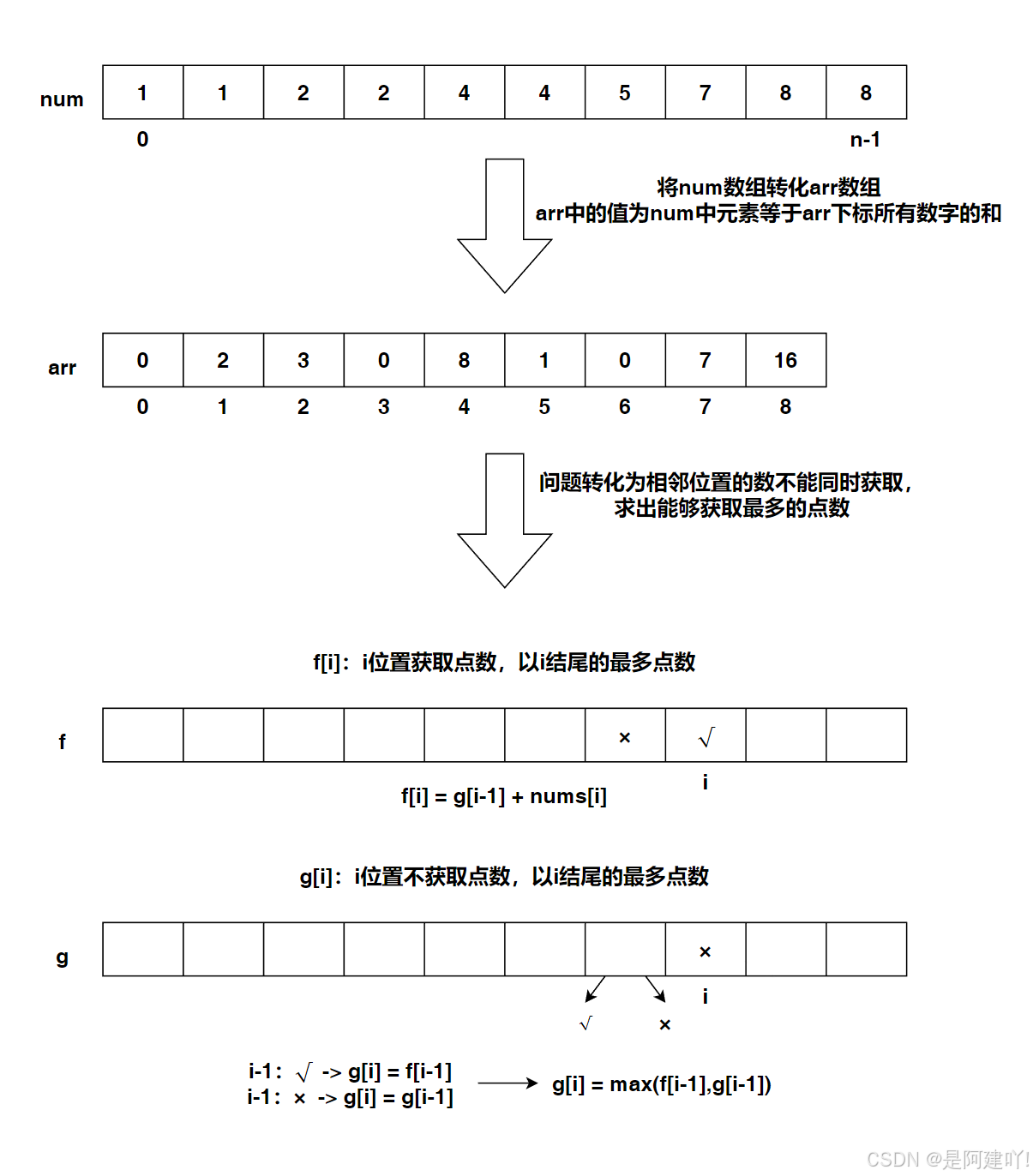
1. 问题转化与预处理：
   • 原问题要求删除一个数 nums[i] 后必须删除 nums[i]-1 和 nums[i]+1，并获得 nums[i] 点数。通过预处理将问题简化：
     • 统计每个数字的总点数：创建数组 arr，其中 arr[x] 表示所有值为 x 的元素的点数总和（即 x 出现次数 × x）
     • 转化为相邻限制问题：选择 x 获得 arr[x] 点数后，不能选择 x-1 和 x+1，等价于 “不能选择相邻数字” 的最大化问题
2. 状态定义：
   • f[i] 表示选择数字 i 时能获得的最大点数
   • g[i] 表示不选择数字 i 时能获得的最大点数
3. 状态转移方程：
   • f[i] = g[i-1] + arr[i]：选择数字 i 时，前一个数字 i-1 必须不选，总点数为不选 i-1 的最大点数加 arr[i]
   • g[i] = max(f[i-1], g[i-1])：不选择数字 i 时，总点数为选择或不选择 i-1 的最大点数
4. 初始化：
   • 预处理数组 arr 大小为 max_num + 1（max_num 是 nums 中的最大元素），初始值为 0
   • 起点初始化：f[0] = arr[0]（选择数字 0 的点数），g[0] = 0（不选择数字 0 的点数）
5. 填写 DP 表：
   • 按照从左到右的顺序，从 i=1 遍历到 max_num，基于前一个数字的 f 和 g 值计算当前值，确保子问题已先求解
6. 结果返回：
   • 最大点数为最后一个数字（max_num）选择或不选择的最大值，即 max(f[n-1], g[n-1])（n = max_num + 1）

编写代码：

class Solution {
public:int deleteAndEarn(vector<int>& nums) {int max_num = 0;for(auto x : nums)if(x > max_num) max_num = x;int n = max_num + 1;vector<int> arr(n , 0);for(auto x : nums)arr[x] += x;vector<int> f(n,0) , g(n,0);f[0] = arr[0];for(int i = 1 ; i < n ; i++){f[i] = g[i-1] + arr[i];g[i] = max(f[i-1],g[i-1]);}return max(f[n-1],g[n-1]);}
};

---

四、粉刷房子

题目描述：

思路讲解：
本道题需要我们计算粉刷房子总花费最少的方案，每个房子可粉刷成红、蓝、绿三种颜色，且相邻房子颜色不能相同，问题可拆解为：第 i 个房子刷成某颜色的最小花费 = 前一个房子刷成其他两种颜色的最小花费（取较小者） + 当前房子刷该颜色的花费。以下是具体思路：

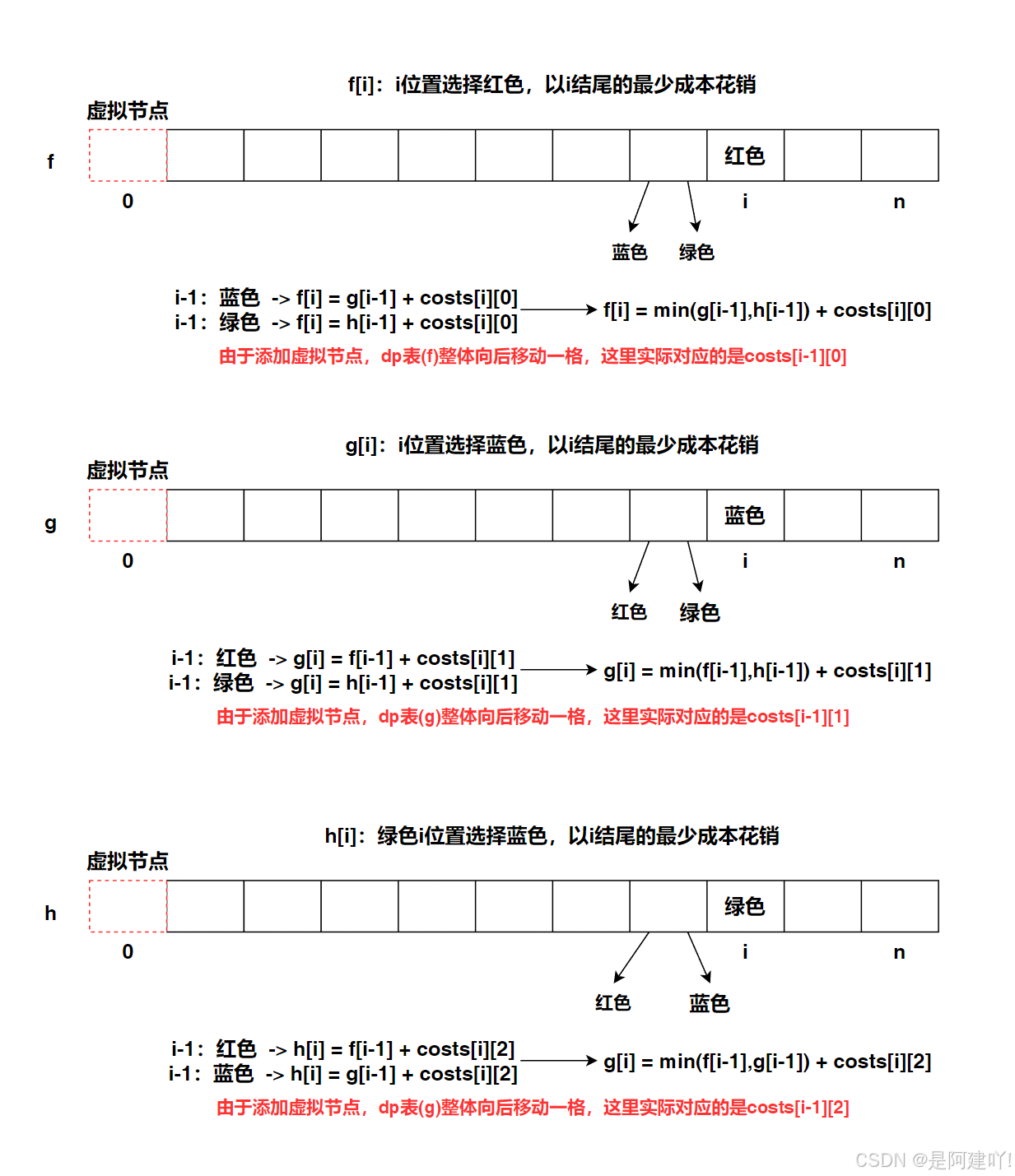
1. 状态表示：
   • f[i] 表示第 i 个房子粉刷成红色的最小总花费
   • g[i] 表示第 i 个房子粉刷成蓝色的最小总花费
   • h[i] 表示第 i 个房子粉刷成绿色的最小总花费
2. 状态转移方程：
   • f[i] = min(g[i-1], h[i-1]) + costs[i-1][0]：第 i 个房子刷红色时，前一个房子只能刷蓝或绿，取两者最小花费加当前红色花费
   • g[i] = min(f[i-1], h[i-1]) + costs[i-1][1]：第 i 个房子刷蓝色时，前一个房子只能刷红或绿，取两者最小花费加当前蓝色花费
   • h[i] = min(f[i-1], g[i-1]) + costs[i-1][2]：第 i 个房子刷绿色时，前一个房子只能刷红或蓝，取两者最小花费加当前绿色花费
3. 初始化：
   • 初始状态 f[0] = g[0] = h[0] = 0：表示粉刷 0 个房子时，三种颜色的花费均为 0（作为递推起点）
4. 填写 DP 表：
   • 按照从左到右的顺序，从第 1 个房子遍历到第 n 个房子（i=1 到 i=n），基于前一个房子的三种颜色花费计算当前房子的三种花费，确保子问题已先求解
5. 结果返回：
   • 最后一个房子（第 n 个）粉刷成三种颜色的最小花费中的最小值，即 min(f[n], min(g[n], h[n]))，即为粉刷所有房子的最少总成本

编写代码：

class Solution {
public:int minCost(vector<vector<int>>& costs) {int n = costs.size();vector<int> f(n+1,0) , g(n+1,0) , h(n+1,0);for(int i = 1 ; i <= n ; i++){f[i] = min(g[i-1],h[i-1]) + costs[i-1][0];g[i] = min(f[i-1],h[i-1]) + costs[i-1][1];h[i] = min(f[i-1],g[i-1]) + costs[i-1][2];}return min(f[n],min(g[n],h[n]));}
};

---

五、买卖股票的最佳时机含冷冻期

题目描述：

思路讲解：
本道题需要我们计算买卖股票的最大利润，股票交易需遵守 “卖出后次日不能买入（冷冻期）” 的规则，可多次买卖但不能同时持有多支股票。以下是具体思路：

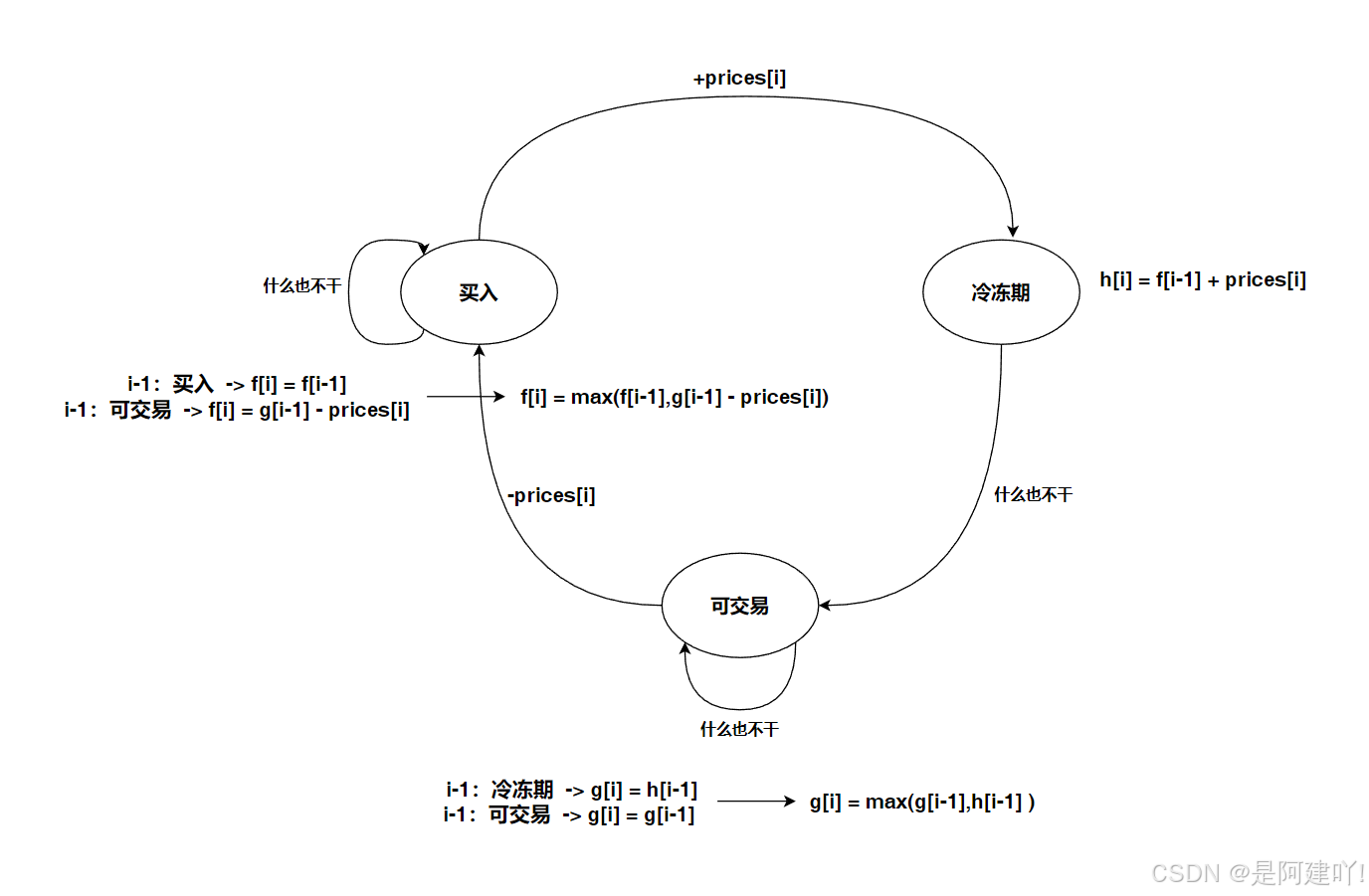
1. 状态定义：
   • 我们可以用三个状态表示每天结束时的不同情况：
     • f[i]：第 i 天结束时持有股票（买入）的最大利润
     • g[i]：第 i 天结束时不持有股票且不处于冷冻期 （可交易）的最大利润
     • h[i]：第 i 天结束时不持有股票且处于冷冻期（冷冻期）的最大利润
2. 递推公式：
   • f[i]（持有股票）：
     • 可能是前一天已经持有股票，即 f[i-1]
     • 也可能是今天买入股票，此时必须保证前一天 不处于冷冻期（即 g[i-1]），然后减去今天的股价 prices[i]
     • 递推公式：f[i] = max(f[i-1], g[i-1] - prices[i])
   • g[i]（不持有股票且不处于冷冻期）：
     • 可能是前一天就不持有股票且不处于冷冻期，即 g[i-1]
     • 也可能是前一天处于冷冻期，今天解冻，即 h[i-1]
     • 递推公式：g[i] = max(g[i-1], h[i-1])
   • h[i]（不持有股票且处于冷冻期）：
     • 只能是 今天卖出了股票，即前一天持有股票 f[i-1] 加上今天的股价 prices[i]
     • 递推公式：h[i] = f[i-1] + prices[i]
3. 初始化：
   • 第 0 天（初始状态）：
     • f[0] = -prices[0]（第一天买入股票，利润为 -prices[0]）
     • g[0] = 0（第一天不持有股票，利润为 0）
     • h[0] = 0（第一天不可能卖出股票，冷冻期利润为 0）
4. 计算顺序：
   • 按照从左到右的顺序，从第 1 天遍历到最后一天（i=1 到 i=n-1），基于前一天的三种状态计算当前状态，确保子问题已先求解
5. 最终结果
   • 最后一天的最大利润应该是：
     • 不持有股票（可能是 g[n-1] 或 h[n-1]）
     • 不能是 f[n-1]，因为最后一天持有股票没有意义（无法卖出）
   • 返回：max(g[n-1], h[n-1])

编写代码：

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<int> f(n,0) , g(n,0) , h(n,0);f[0] = 0 - prices[0];for(int i = 1 ; i < n ; i++){f[i] = max(f[i-1],g[i-1] - prices[i]);g[i] = max(g[i-1],h[i-1] );h[i] = f[i-1] + prices[i];}return max(g[n-1],h[n-1]);}
};

---

六、买卖股票的最佳时机含手续费

题目描述：

思路讲解：
本道题需要我们计算买卖股票获得利润的最大值，股票可无限次交易，但每笔交易（买入后卖出）需支付一次手续费，且不能同时持有多支股票，问题需区分两种状态：持有和不持有股票，我们可以通过定义两种状态数组分别记录持有和不持有股票时的最大利润，最后返回最后一天不持有股票时的最大利润。以下是具体思路：

1. 状态表示：
   • f[i] 表示第 i 天持有股票（买入）时的最大利润
   • g[i] 表示第 i 天不持有股票（可交易）时的最大利润
2. 状态转移方程：
   • f[i] = max(f[i-1], g[i-1] - prices[i])：第 i 天持有股票，要么是前一天就持有（继续持有，利润不变），要么是前一天不持有（当天买入，利润为前一天不持有利润减去当天股价）
   • g[i] = max(f[i-1] + prices[i] - fee, g[i-1])：第 i 天不持有股票，要么是前一天持有（当天卖出，利润为前一天持有利润加上当天股价再减去手续费），要么是前一天就不持有（未操作，利润不变）
3. 初始化：
   • 第 0 天：f[0] = -prices[0]（买入当天股票，利润为负股价），g[0] = 0（不持有股票，利润为 0）
4. 填写 DP 表：
   • 按照从左到右的顺序，从第 1 天遍历到最后一天（i=1 到 i=n-1），基于前一天的两种状态计算当前状态，确保子问题已先求解
5. 结果返回：
   • 最后一天不持有股票时的最大利润为 g[n-1]（持有股票无法获得最终利润），即为最大总利润

编写代码：

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();vector<int> f(n,0),g(n,0);f[0] = -prices[0];for(int i = 1 ; i < n ; i++){f[i] = max(f[i-1],g[i-1] - prices[i]);g[i] = max(f[i-1] + prices[i] - fee,g[i-1]) ;}return g[n-1];}
};

---

七、买卖股票的最佳时机 III

题目描述：

思路讲解：
本道题需要我们计算买卖股票所能获取的最大利润，股票最多可完成两笔交易（买入并卖出），且不能同时持有多支股票，所以问题需要区分交易次数和持有状态。以下是具体思路：

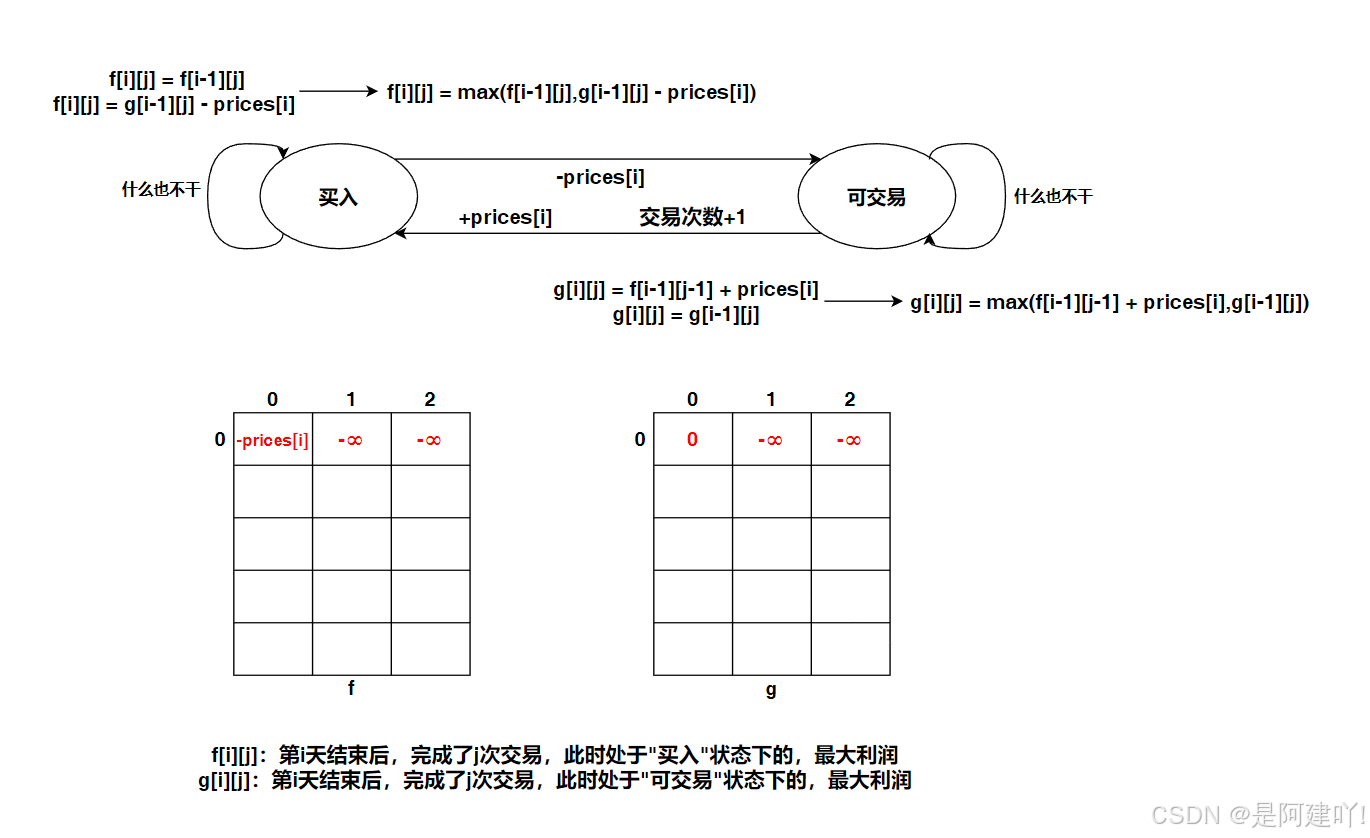
1. 状态表示：
   • f[i][j] 表示第 i 天持有股票，且已完成 j 笔交易（买入未卖出）时的最大利润
   • g[i][j] 表示第 i 天不持有股票，且已完成 j 笔交易时的最大利润
2. 状态转移方程：
   • f[i][j] = max(f[i-1][j], g[i-1][j] - prices[i])
     • 第 i 天持有股票且完成 j 笔交易，要么是前一天就持有（继续持有，交易次数不变），要么是前一天不持有（当天买入，交易次数不变，利润减去当天股价）
   • 当 j=0 时：g[i][0] = g[i-1][0]（无法完成交易，利润不变）
   • 当 j≥1 时：g[i][j] = max(f[i-1][j-1] + prices[i], g[i-1][j])
     • 第 i 天不持有股票且完成 j 笔交易，要么是前一天持有（当天卖出，交易次数加 1，利润加上当天股价），要么是前一天就不持有（交易次数不变，利润不变）
3. 初始化：
   • 第 0 天：f[0][0] = -prices[0]（买入股票，0 笔完成交易）；其余状态（f[0][1]、f[0][2]、g[0][1]、g[0][2]）初始化为极小值（表示不可能存在的状态）；g[0][0] = 0（不持有股票，0 笔交易）
4. 填写 DP 表：
   • 按照从上到下，从左到右的顺序，外层循环从第 1 天遍历到最后一天（i=1 到 i=n-1），内层循环遍历交易次数（j=0 到 j=2），基于前一天的状态计算当前状态，确保子问题已先求解
5. 结果返回：
   • 最后一天不持有股票时，0、1、2 笔交易的最大利润中的最大值，即 max(g[n-1][0], g[n-1][1], g[n-1][2])

编写代码：

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> f(n,vector<int>(3,0));vector<vector<int>> g(n,vector<int>(3,0));f[0][1] = f[0][2] = g[0][1] = g[0][2] = -0x3f3f3f3f;f[0][0] = -prices[0];for(int i = 1 ; i < n ; i++){for(int j = 0 ; j <= 2 ; j++){f[i][j] = max(f[i-1][j],g[i-1][j] - prices[i]);if(j - 1 < 0)g[i][j] = g[i-1][j];elseg[i][j] = max(f[i-1][j-1] + prices[i],g[i-1][j]);}}return max(g[n-1][0] , max(g[n-1][1] , g[n-1][2]));}
};

---

八、买卖股票的最佳时机 IV

题目描述：

思路讲解：
本道题需要我们计算买卖股票所能获取的最大利润，股票最多可完成k笔交易（买入并卖出），且不能同时持有多支股票，所以问题需要区分交易次数和持有状态。以下是具体思路：

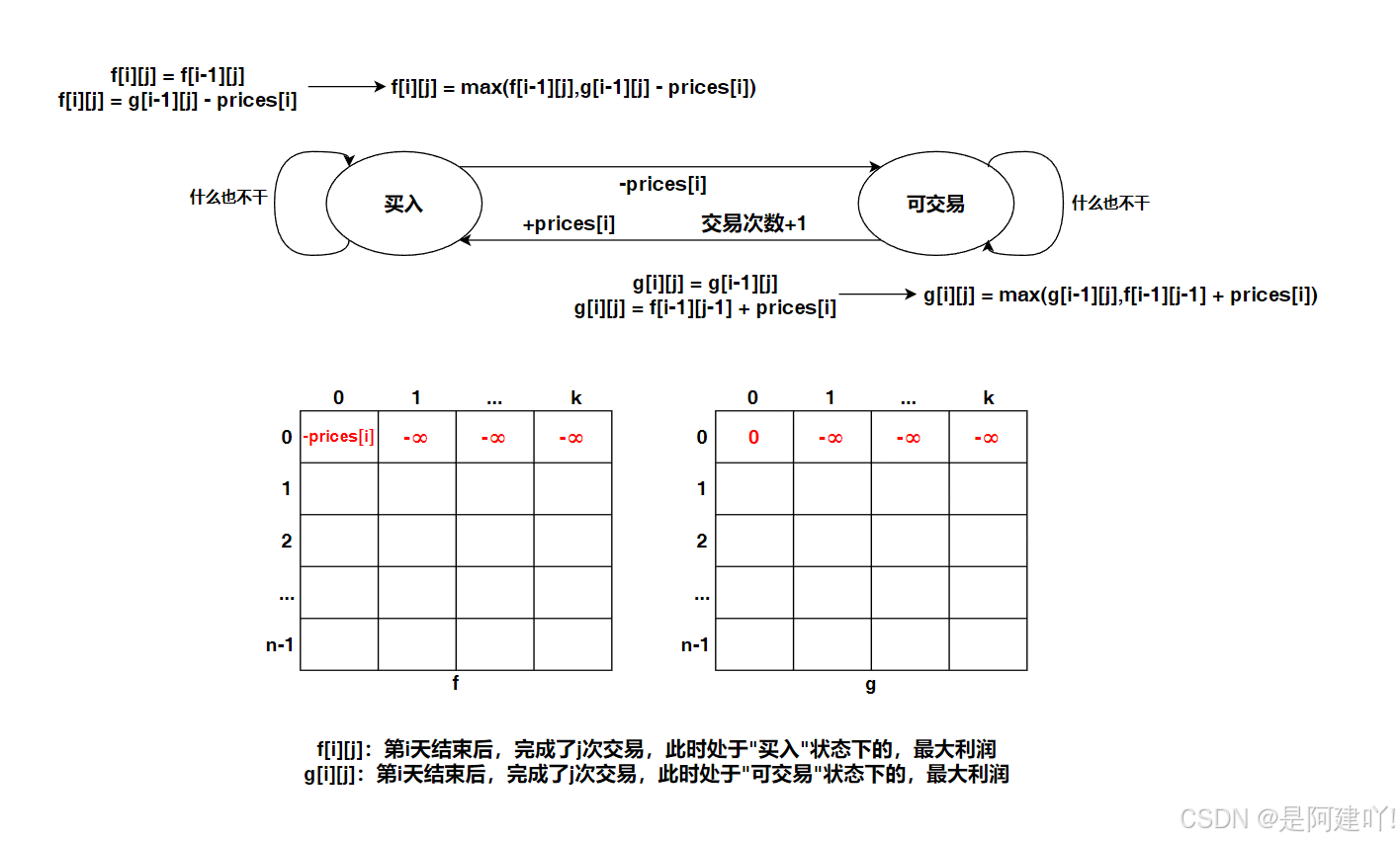
1. 状态表示：
   • f[i][j] 表示第 i 天持有股票，且已完成 j 笔交易（当前持有为第 j+1 笔的买入状态）时的最大利润
   • g[i][j] 表示第 i 天不持有股票，且已完成 j 笔交易时的最大利润
     （j 范围为 0 到 k，分别表示 0 到 k 笔交易）
2. 状态转移方程：
   • f[i][j] = max(f[i-1][j], g[i-1][j] - prices[i])
     • 第 i 天持有股票且完成 j 笔交易，要么是前一天就持有（继续持有，交易次数不变），要么是前一天不持有（当天买入，交易次数不变，利润减去当天股价）
   • 当 j=0 时：g[i][0] = g[i-1][0]（无法完成交易，利润不变）
   • 当 j≥1 时：g[i][j] = max(g[i-1][j], f[i-1][j-1] + prices[i])
     • 第 i 天不持有股票且完成 j 笔交易，要么是前一天就不持有（交易次数不变，利润不变），要么是前一天持有（当天卖出，交易次数加 1，利润加上当天股价）
3. 初始化：
   • 第 0 天：f[0][0] = -prices[0]（买入股票，0 笔完成交易）；g[0][0] = 0（不持有股票，0 笔交易）；其余状态（f[0][j]、g[0][j] 当 j≥1 时）初始化为极小值（表示不可能存在的状态）
4. 填写 DP 表：
   • 按照从上到下，从左到右的顺序，外层循环从第 1 天遍历到最后一天（i=1 到 i=n-1），内层循环遍历交易次数（j=0 到 j=k），基于前一天的状态计算当前状态，确保子问题已先求解
5. 结果返回：
   • 最后一天不持有股票时，0 到 k 笔交易的最大利润中的最大值，即遍历 g[n-1][0…k] 取最大值

编写代码：

class Solution {
public:int maxProfit(int k, vector<int>& prices) {int n = prices.size();vector<vector<int>> f(n,vector<int>(k+1,-0x3f3f3f3f));vector<vector<int>> g(n,vector<int>(k+1,-0x3f3f3f3f));f[0][0] = -prices[0];g[0][0] = 0;for(int i = 1 ; i < n ; i++){for(int j = 0 ; j <= k ; j++){f[i][j] = max(f[i-1][j],g[i-1][j] - prices[i]);if(j - 1 < 0)g[i][j] = g[i-1][j];else g[i][j] = max(g[i-1][j],f[i-1][j-1] + prices[i]);}}int ret = 0;for(int i = 0 ; i <= k ; i++){ret = max(ret,g[n-1][i]);}return ret;}
};

---

结尾

如果有什么建议和疑问，或是有什么错误，大家可以在评论区中提出。
希望大家以后也能和我一起进步！！🌹🌹
如果这篇文章对你有用的话，希望大家给一个三连支持一下！！🌹🌹