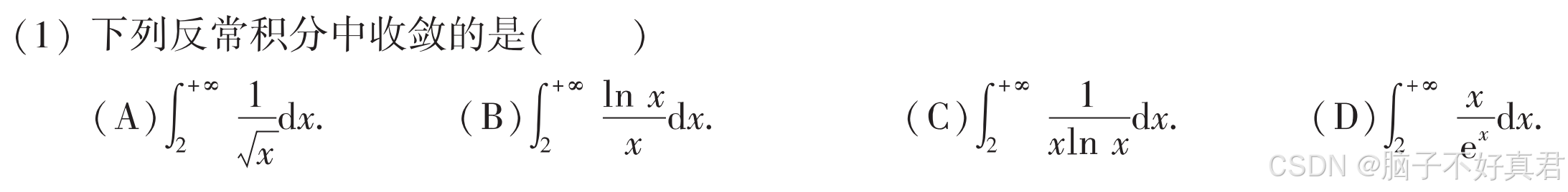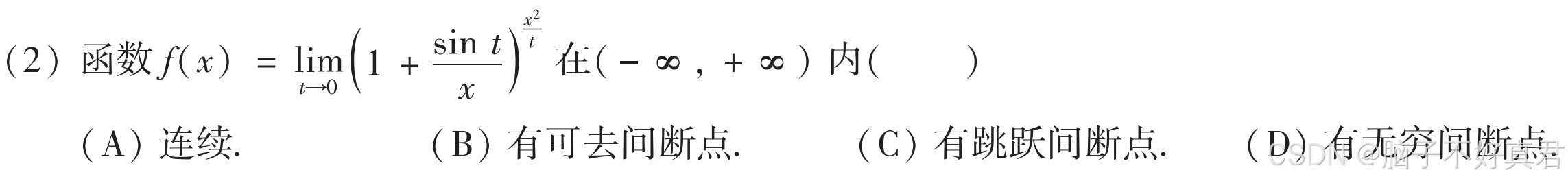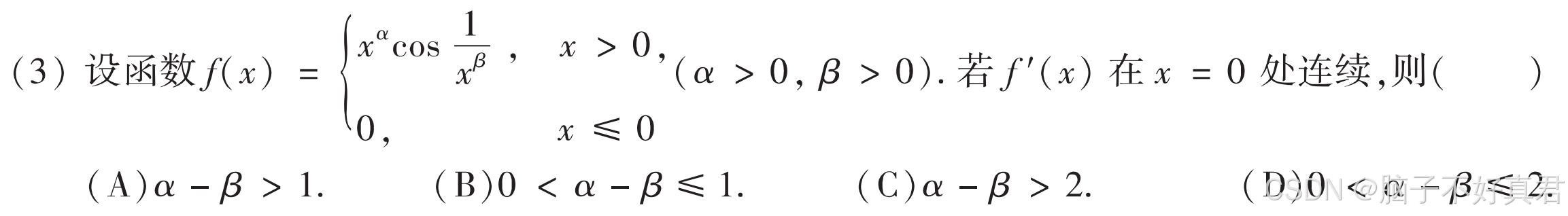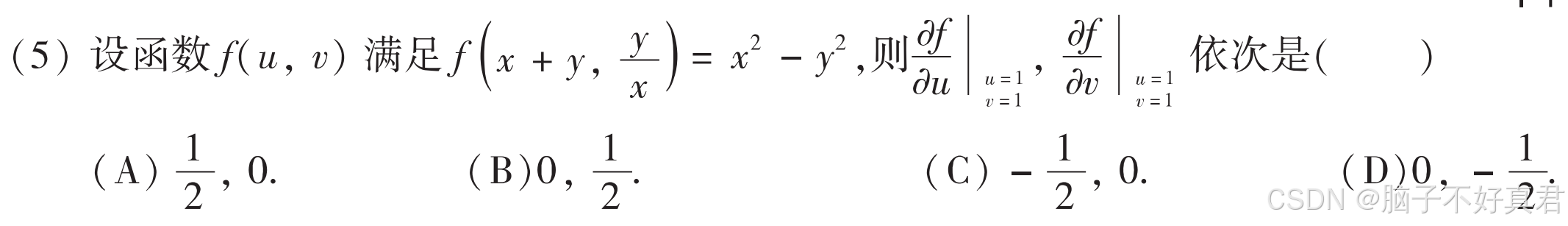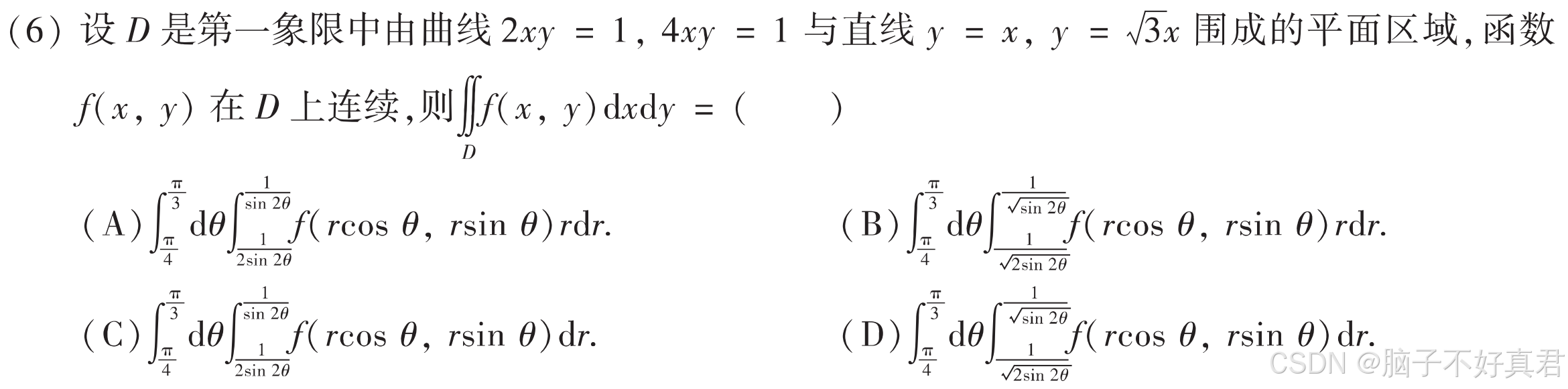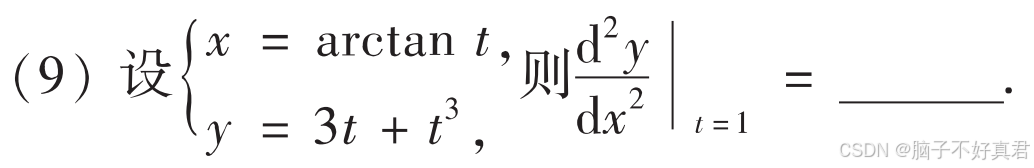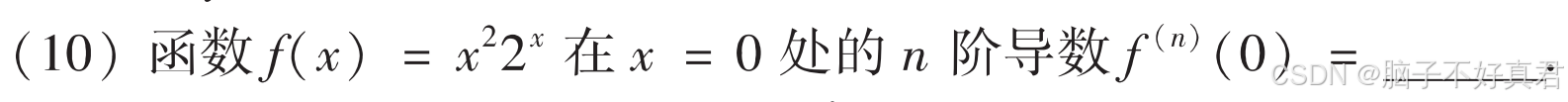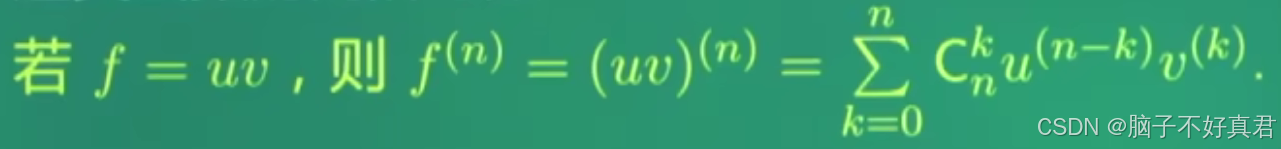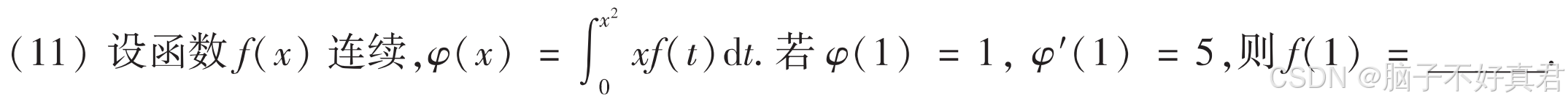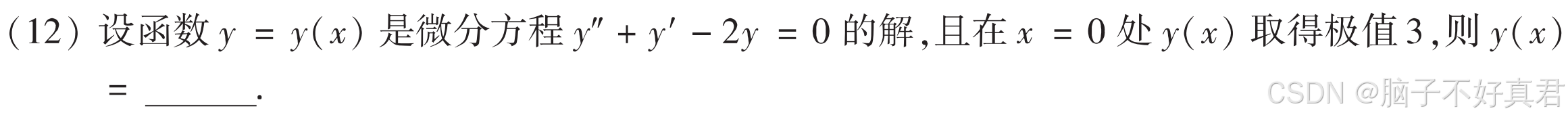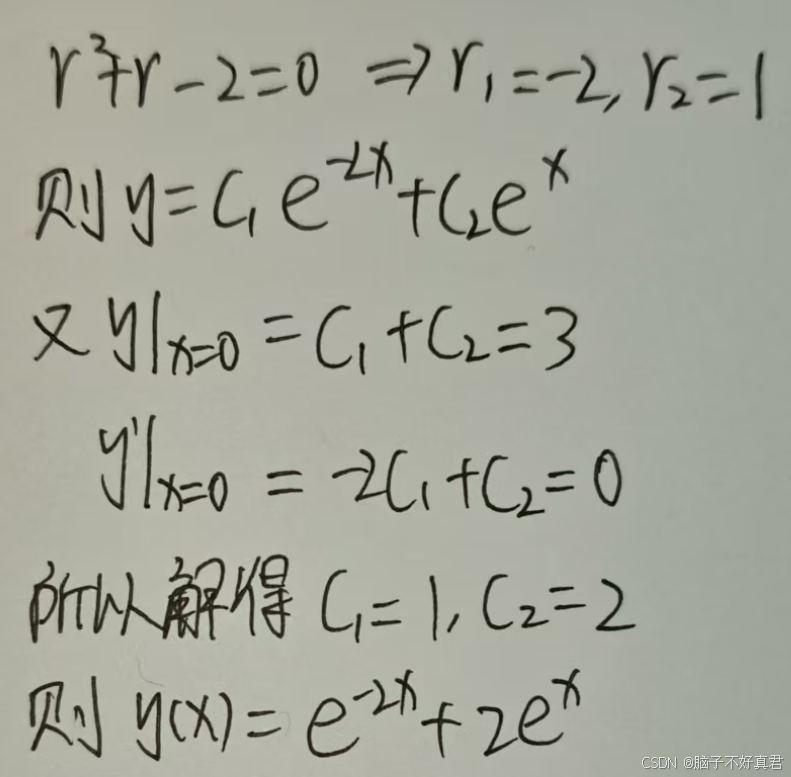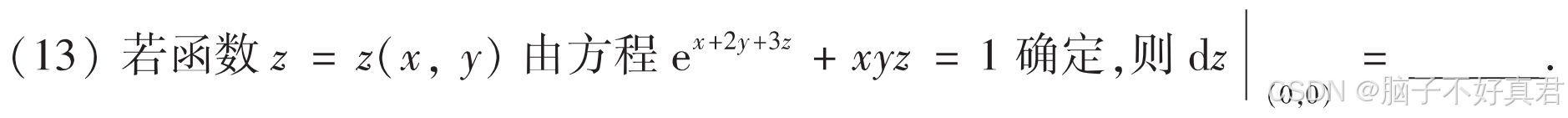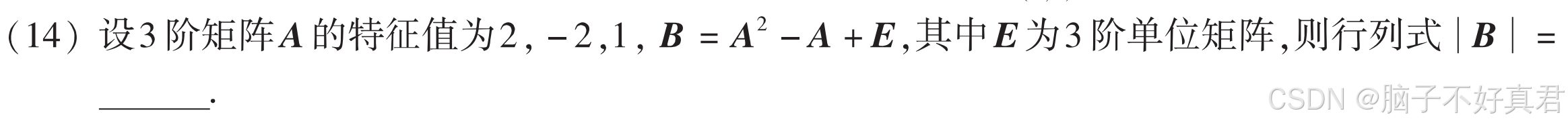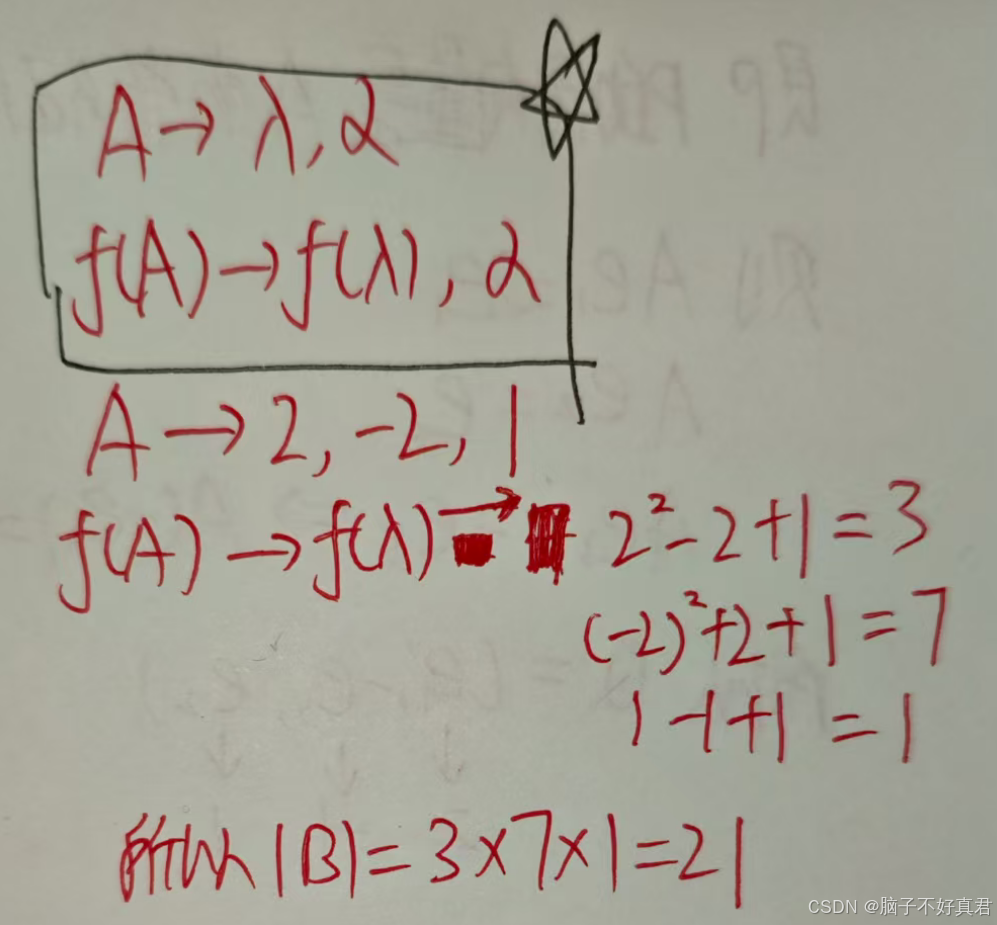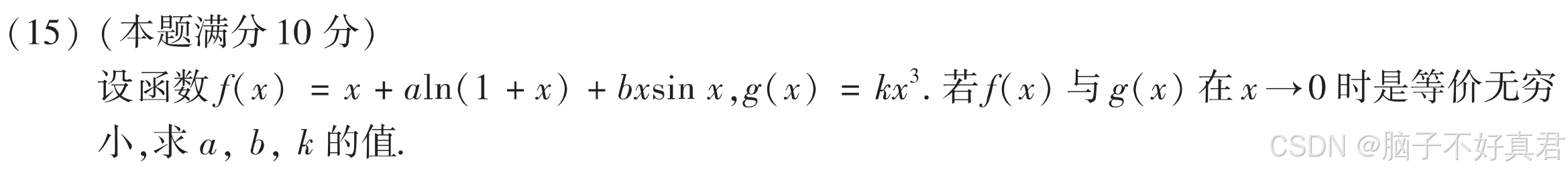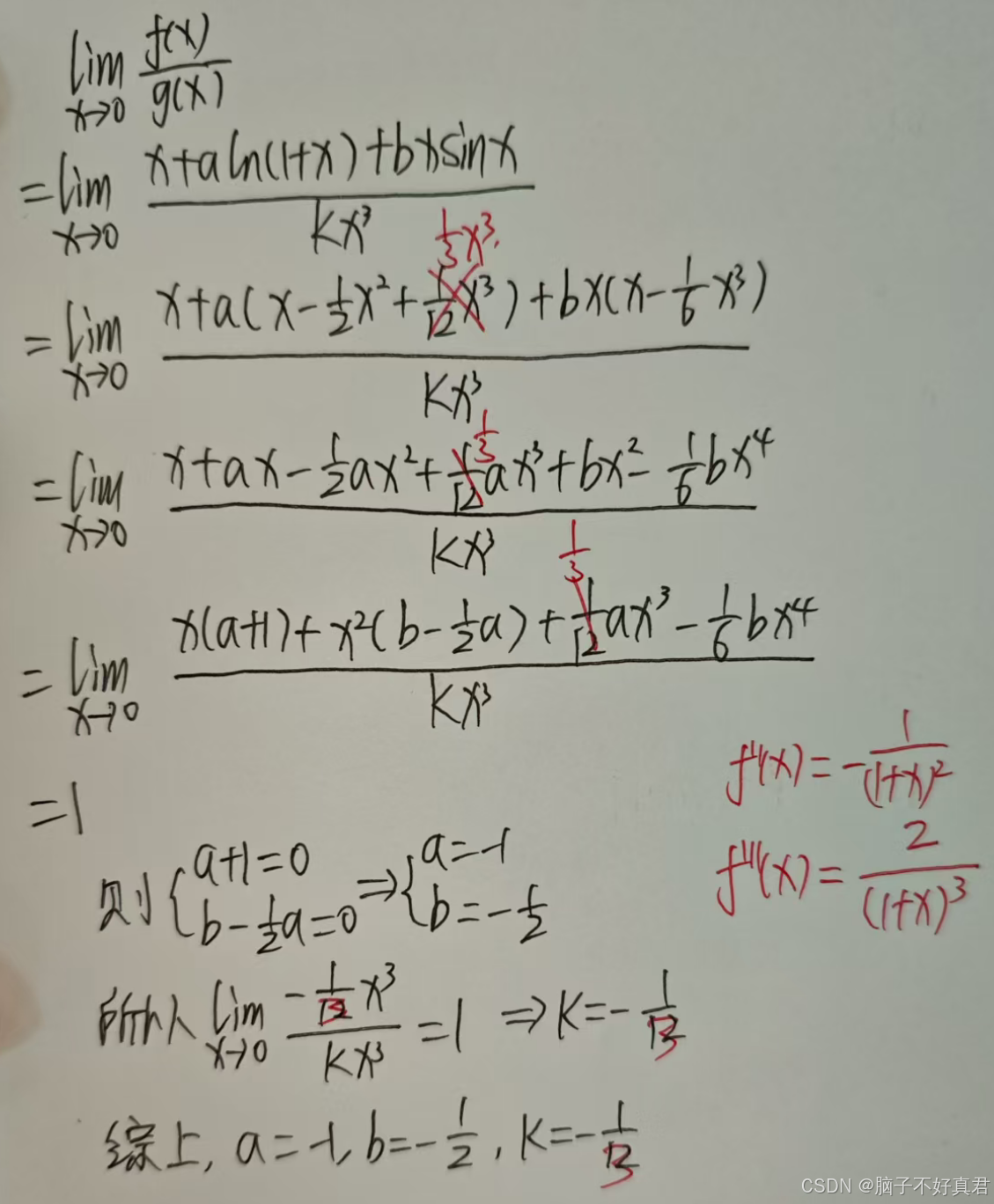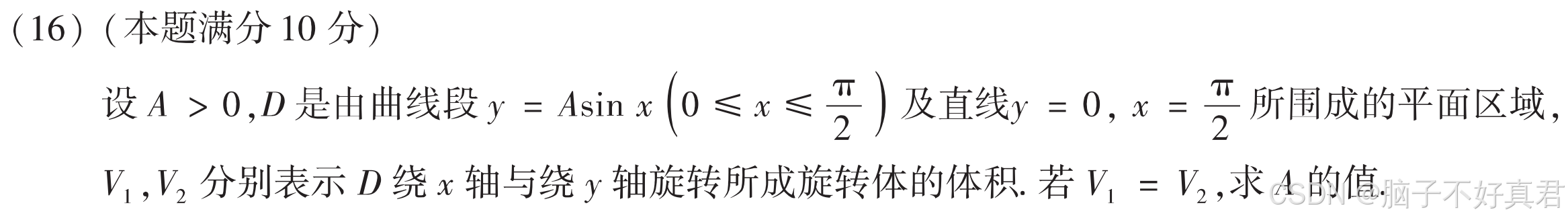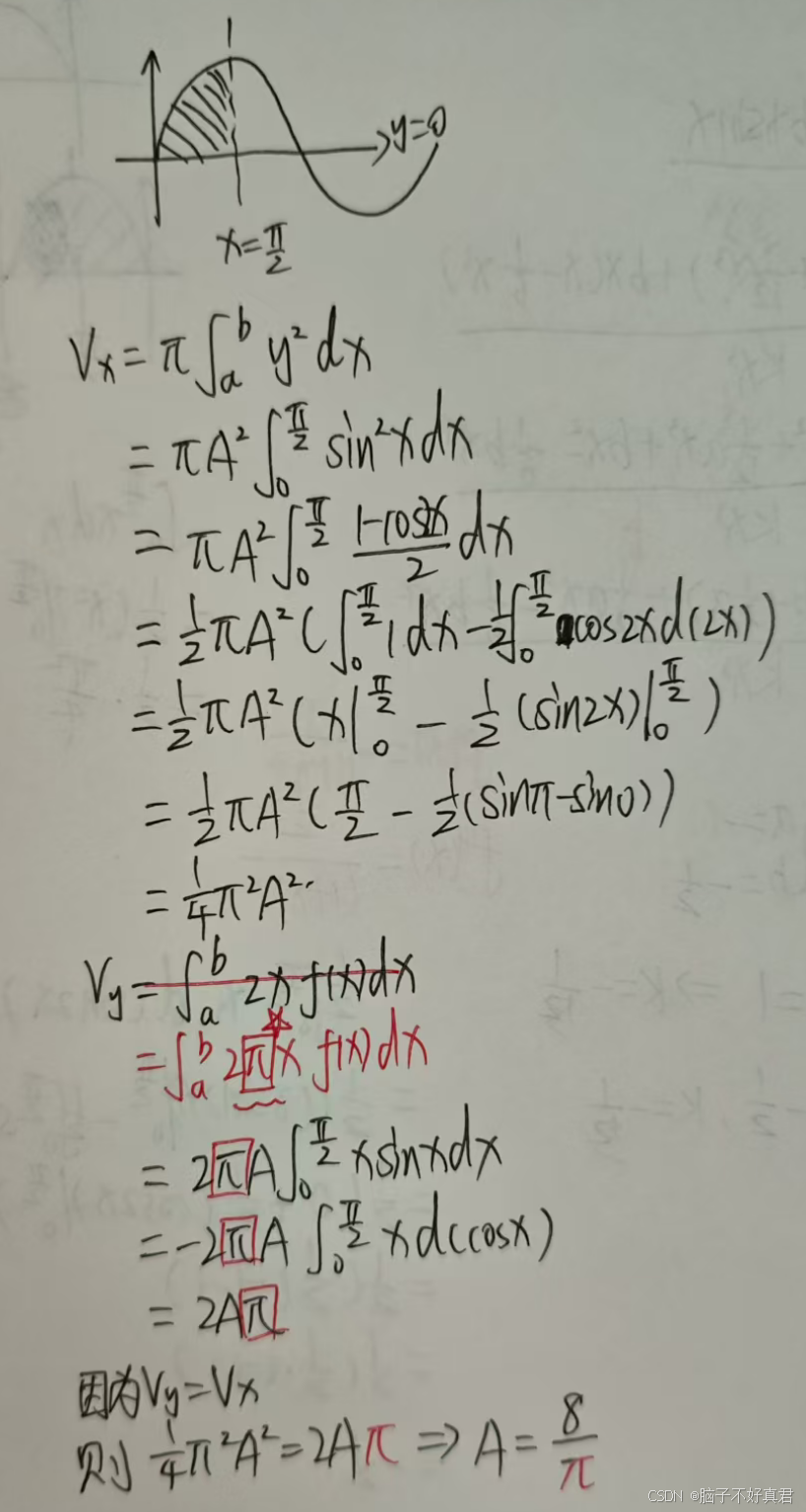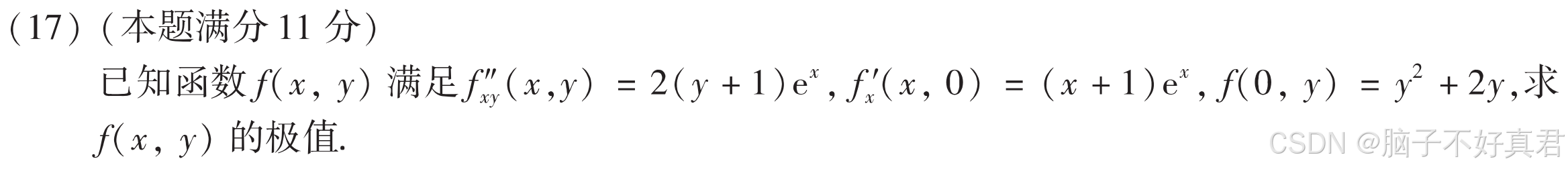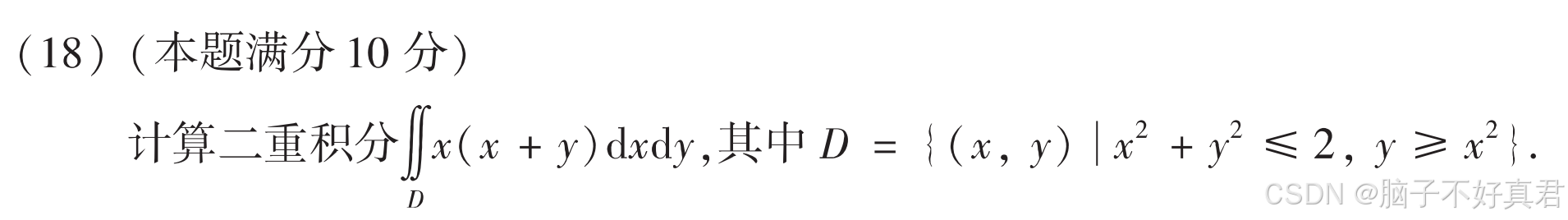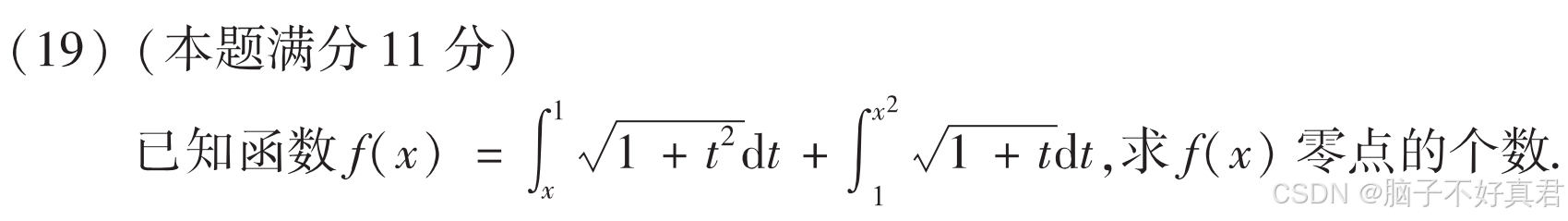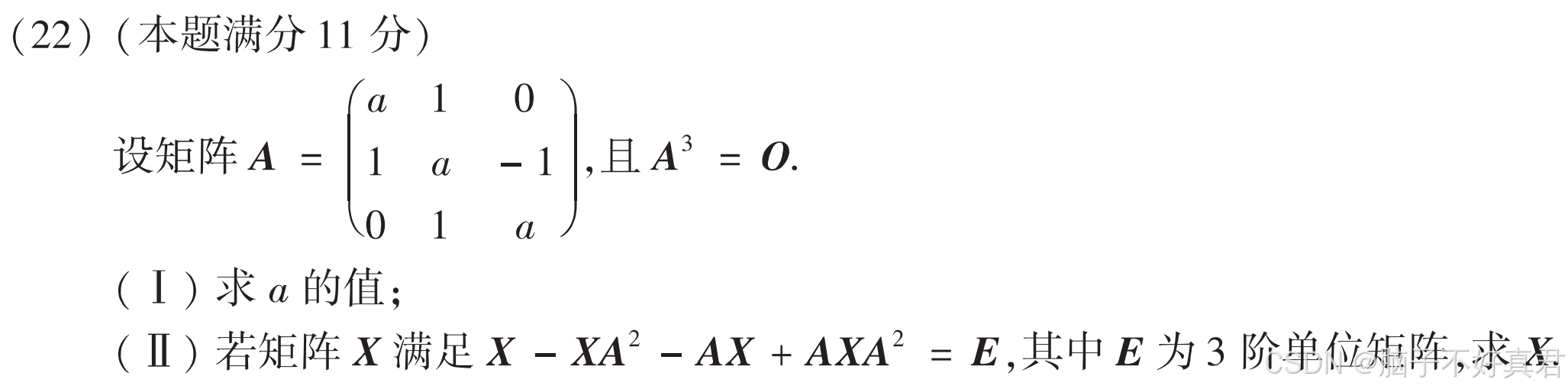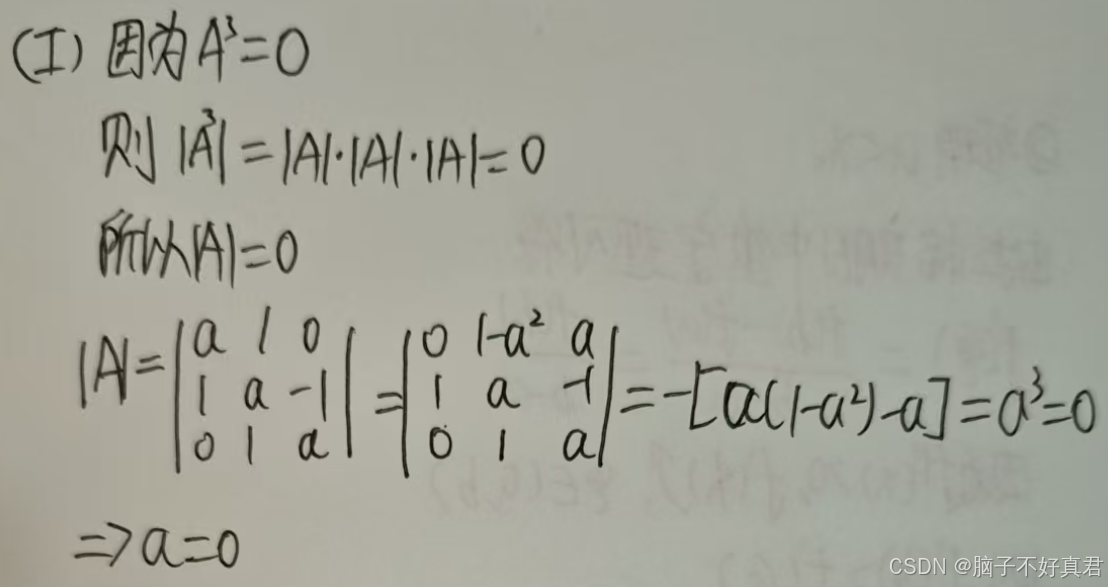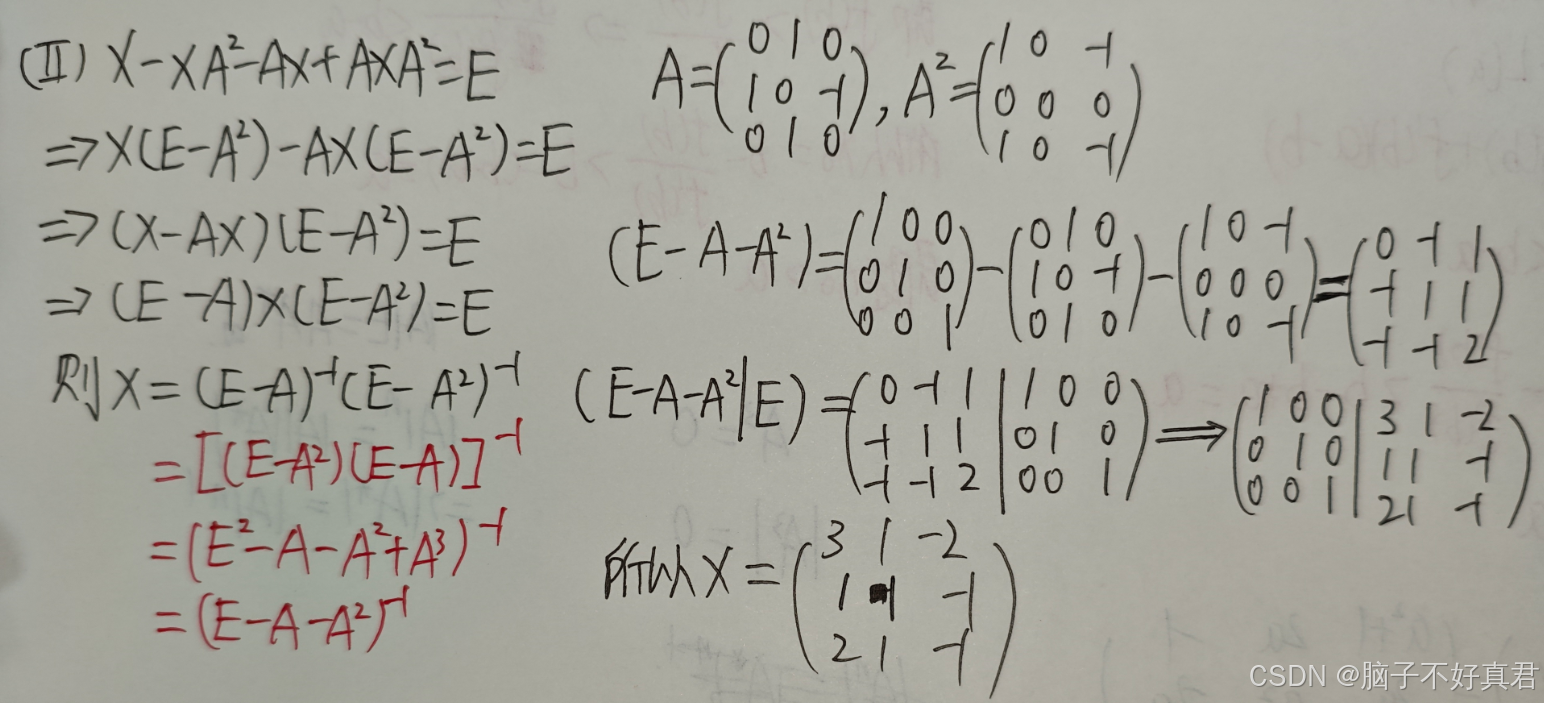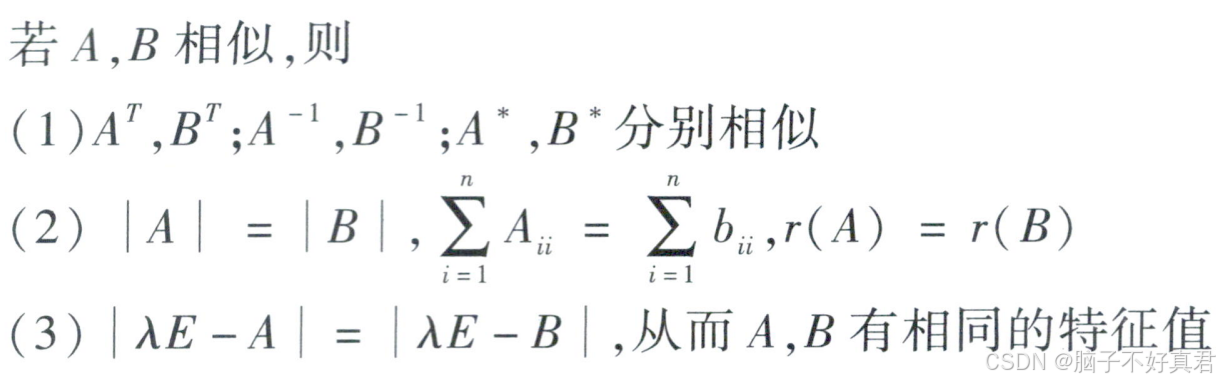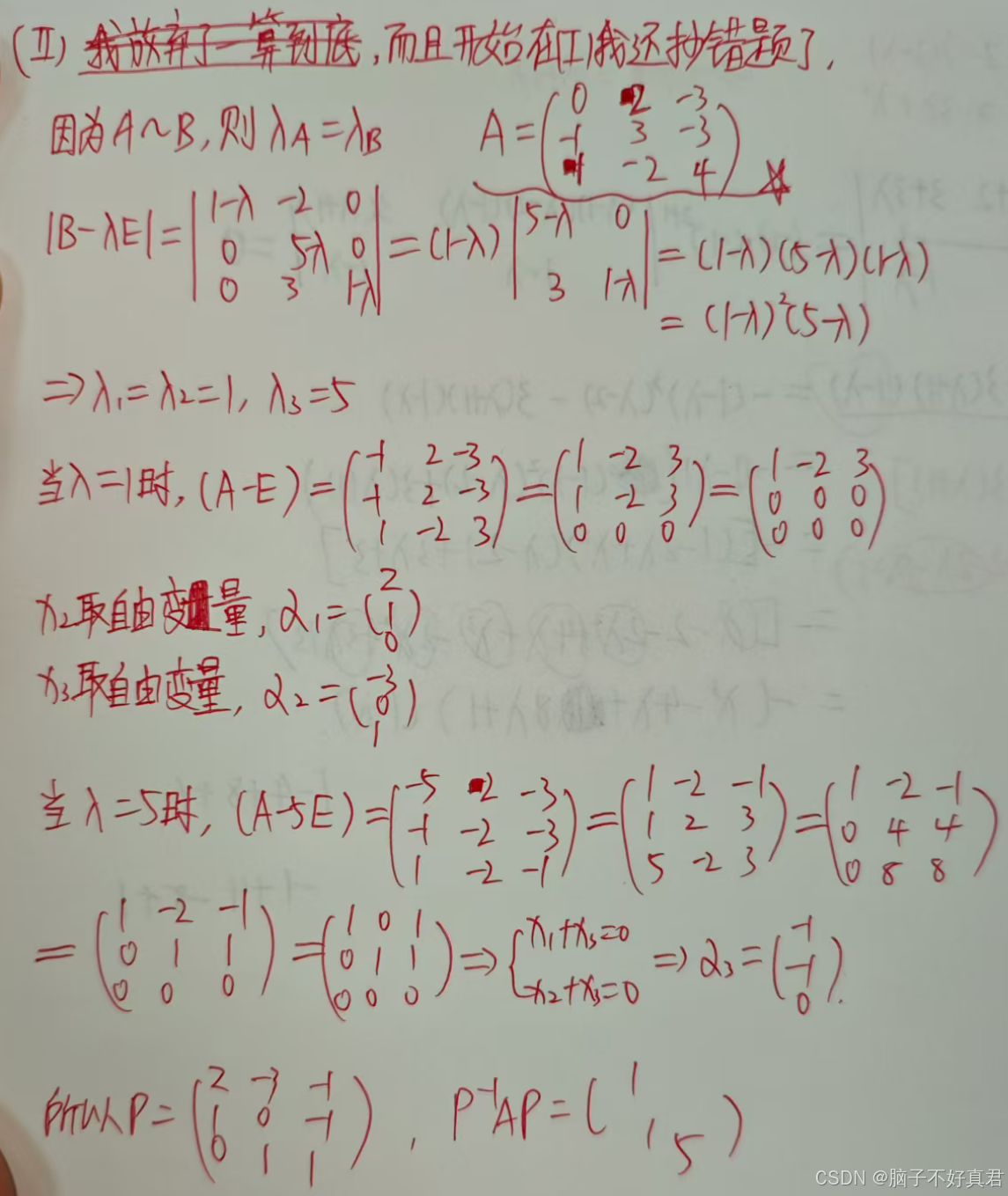2015考研数学(二)真题
一、选择题
(1)
考点:积分区间无穷的反常积分计算、
指数函数增长速率远大于幂函数
(2)
考点:要计算出 用另一个变量极限表示的 f(x) 的表达式,先把 x 看作常数求得 f(x) 表达式
可去间断点的定义
跳跃间断点的定义
无穷间断点的定义
(3)
考点:导函数连续的定义、
导数的定义式、
项的合并
(4)
考点:拐点是使得二阶导不存在的点或等于0的点
(5)
考点:二元函数求一阶偏导、
复习:二元函数求二阶偏导
(6)
考点:二重积分的直角坐标转极坐标、
三个重要关系、
r 由 dxdy 产出
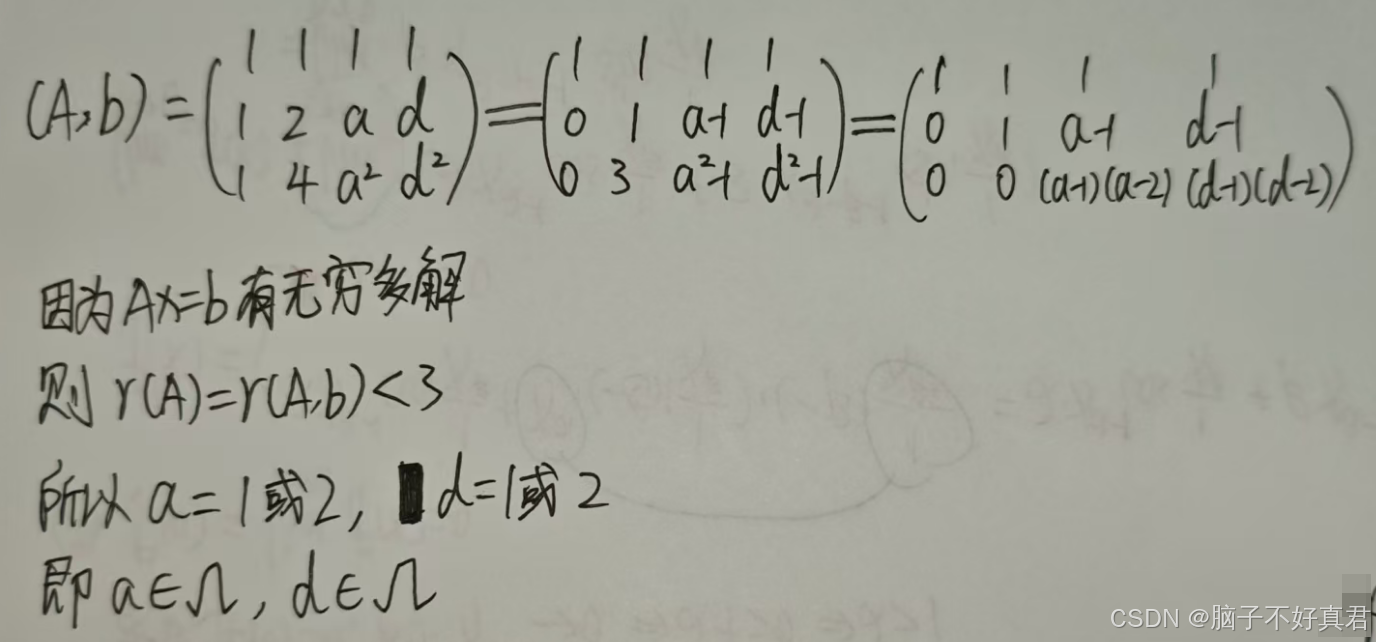
(7)
考点:无穷多解时矩阵与增广矩阵秩的情况
(8)
考点:二次型的标准矩阵定义式、
倍乘初等矩阵、交换初等矩阵、
如果 f 在正交变换 x=py 下的标准形为 某y的平方项式子,那么P^T AP = 这个y的平方项式子的系数对角矩阵P^T AP = 这个y的平方项式子的系数对角矩阵、
在正交变换 x=Py下,将二次型 f=x^T Ax化为标准形,其正交矩阵 P的列向量就是矩阵 A 的(单位正交)特征向量。(P的列向量是A的特征向量、Q的列向量也是A的特征向量)、
Aα= λα
方法一:
二次型的标准矩阵定义式、
倍乘初等矩阵、交换初等矩阵、
如果 f 在正交变换 x=py 下的标准形为 某y的平方项式子,那么P^T AP = 这个y的平方项式子的系数对角矩阵P^T AP = 这个y的平方项式子的系数对角矩阵
方法二:
在正交变换 x=Py下,将二次型 f=x^T Ax化为标准形,其正交矩阵 P的列向量就是矩阵 A 的(单位正交)特征向量。(P的列向量是A的特征向量、Q的列向量也是A的特征向量)、
Aα= λα
二、填空题
(9)
考点:参数方程求二阶导
(10)
考点:莱布尼茨公式
★错过两次了(11)
考点:定积分内不含积分上下限变量,使用提出变量或者换元法解决
★(12)
考点:别总代错将一阶导函数当作原函数
(13)
考点:隐函数求导、全微分公式
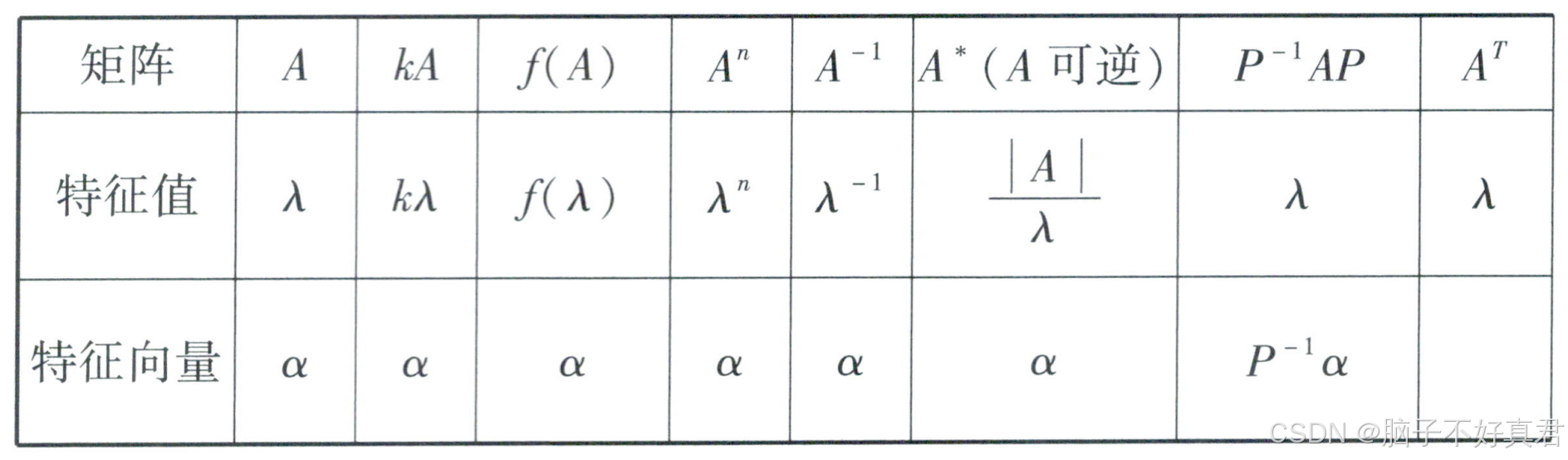
(14)
考点:⬇
三、解答题
(15)
考点:分子要泰勒展开到与分母同次幂、
细心计算!
(16)
考点:圆盘法、
柱壳法、
绕x轴,绕y轴的旋转体体积计算公式
(17)
考点:不定积分还原函数、
二元函数极值求法、
D = AC - B^2
★犯了很多次了,看到二重积分秒想到普通对称性和轮换对称性(若积分区域关于y=x对称)(18)
考点:普通对称性、
三角换元、
犯了很多次了,看到二重积分秒想到普通对称性和轮换对称性(若积分区域关于y=x对称)
(19)
考点:变限积分求导、
技巧、
零点定理、
定积分结果正负取决于积分上下限和被积函数的正负
(20)
考点:微分方程的物理应用、
y 与 x 成正比即 y/x=k, 可写作 y=kx, 所以两个变量成正比即一边乘以比例系数
(21)
考点:画图、
切线方程、
思路(构造不等式)、
凹函数的性质(方法一)、
拉格朗日中值定理(方法二)
方法一:
方法二:
(22)
考点:|AB|=|A||B|(方法一)、
Aα= λα(方法二)、
零矩阵的特征值全为0、
B^-1 A^-1 = (AB)^-1
(Ⅰ)
方法一:
方法二:
(Ⅱ)
★(23)
我抄掉了一堆负号
考点:我抄题都抄错了,很多次、
A~B的结论👇、
P^-1 AP = A的特征值组成的对角矩阵、
一般相似对角化 (P^−1 AP=Λ),特征向量不需要单位化, 正交化、
实对称矩阵的正交相似对角化 (P^T AP=Λ), 特征向量需要单位化, 正交化、
用正交变换化二次型为标准形, 特征向量需要单位化, 正交化(Ⅰ)
(Ⅱ)