【LeetCode每日一题】48. 旋转图像 240. 搜索二维矩阵 II

2025.8.27

48. 旋转图像

题目

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

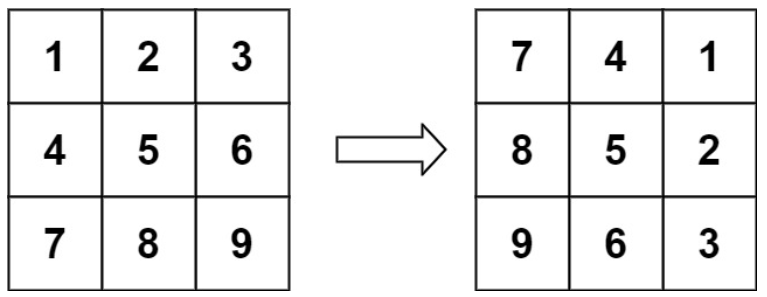
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

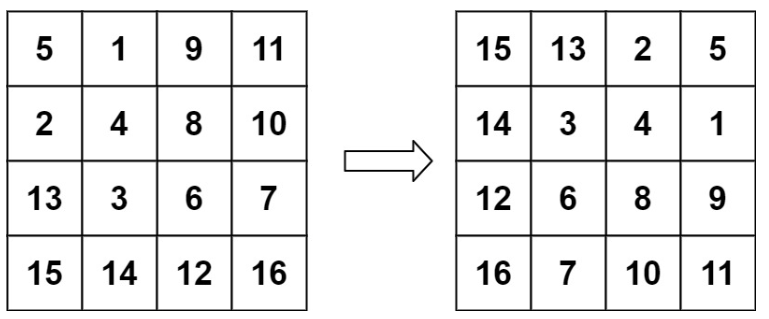
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

总体思路

方法一：

初始化边界：left=0, right=n-1

逐层处理：从外层到内层循环

元素交换：每层中每次同时旋转4个元素

边界收缩：完成一层后边界向内收缩

时间复杂度：O(n²)，需要访问矩阵中的每个元素一次

空间复杂度：O(1)，只使用了常数级别的额外空间

方法二：

采用分步处理的策略，将90度顺时针旋转分解为两个简单的操作：

转置矩阵：沿主对角线翻转（行变列，列变行）

水平翻转：将每一行进行镜像翻转

原始矩阵：    转置后：     水平翻转后：
[1,2,3]      [1,4,7]     [7,4,1]
[4,5,6]  →   [2,5,8]  →  [8,5,2]
[7,8,9]      [3,6,9]     [9,6,3]

时间复杂度：O(n²)

空间复杂度：O(1)

代码

golang

方法一：

func rotate(matrix [][]int) {n := len(matrix)if n == 0 {return}left, right := 0, n-1for left < right {// 遍历当前层的每个元素（除了最后一个，因为会被覆盖）for i := 0; i < right-left; i++ {top, bottom := left, right// 保存左上角的元素topLeft := matrix[top][left+i]// 左下角 → 左上角matrix[top][left+i] = matrix[bottom-i][left]// 右下角 → 左下角matrix[bottom-i][left] = matrix[bottom][right-i]// 右上角 → 右下角matrix[bottom][right-i] = matrix[top+i][right]// 保存的左上角 → 右上角matrix[top+i][right] = topLeft}// 缩小边界，进入内层left++right--}
}

// 纯享！！！
func rotate(matrix [][]int)  {n := len(matrix)if n == 0 {return}left, right := 0, n-1for left < right {for i := 0; i < right-left; i++ {top, bottom := left, righttopleft := matrix[top][left+i]matrix[top][left+i] = matrix[bottom-i][left]matrix[bottom-i][left] = matrix[bottom][right-i]matrix[bottom][right-i] = matrix[top+i][right]matrix[top+i][right] = topleft}left++right--}
}

方法二：

func rotate(matrix [][]int) {n := len(matrix)if n == 0 {return}// 第一步：转置矩阵（沿主对角线翻转）for i := 0; i < n; i++ {// j从i开始，只处理上三角或下三角，避免重复交换for j := i; j < n; j++ {// 交换 matrix[i][j] 和 matrix[j][i]// 这将行变为列，列变为行matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]}}// 第二步：水平翻转每一行（镜像对称）for i := 0; i < n; i++ {// 只需遍历前半部分元素，与对应的后半部分元素交换for j := 0; j < n/2; j++ {// 交换当前行中对称位置的元素// matrix[i][j] 与 matrix[i][n-1-j] 交换matrix[i][j], matrix[i][n-1-j] = matrix[i][n-1-j], matrix[i][j]}}
}

// 纯享！！！
func rotate(matrix [][]int) {n := len(matrix)if n == 0 {return}for i := 0; i < n; i++ { for j := i; j < n; j++ {matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]}}for i := 0; i < n; i++ {for j := 0; j < n/2; j++ {matrix[i][j], matrix[i][n-1-j] = matrix[i][n-1-j], matrix[i][j]}}
}

240. 搜索二维矩阵 II

题目

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例 1：

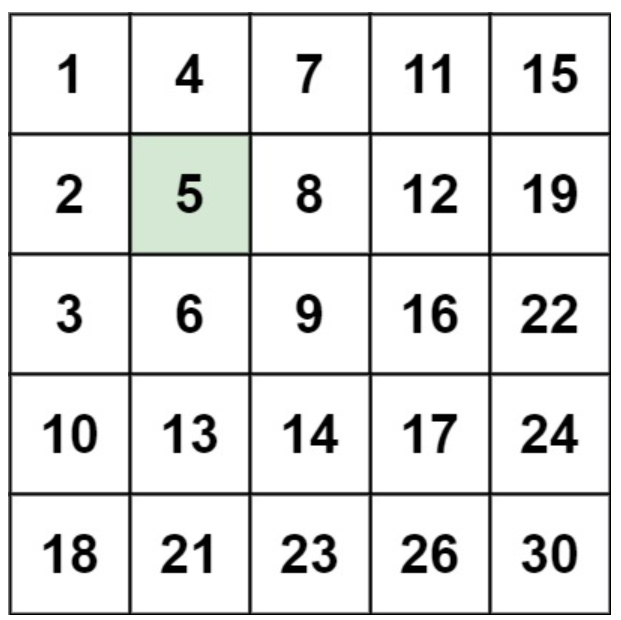
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true
示例 2：

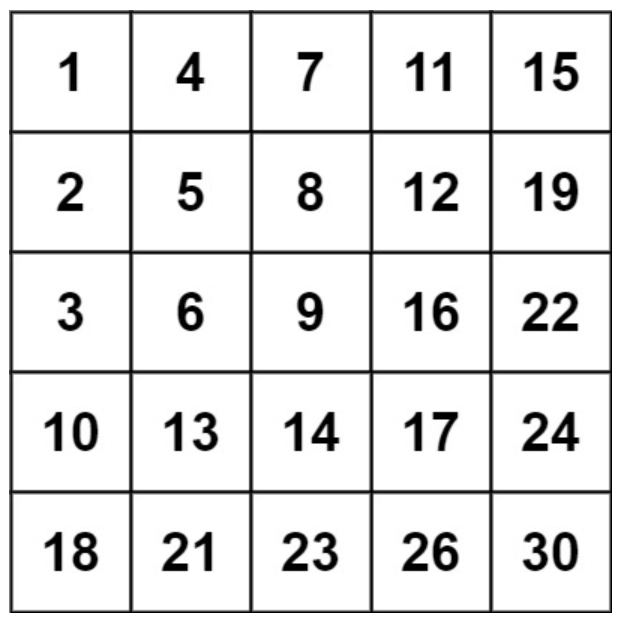
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matrix[i][j] <= 109
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 109

总体思路

这个算法采用右上角起点搜索法：

• 起点选择：从矩阵的右上角开始（第一行最后一列）

• 比较策略：

  • 如果当前值等于目标值，返回 true

  • 如果当前值小于目标值，向下移动（因为这一列下面的值更大）

  • 如果当前值大于目标值，向左移动（因为这一行左边的值更小）

• 终止条件：当行或列超出矩阵边界时停止

时间复杂度：O(m + n)，其中m是行数，n是列数

空间复杂度：O(1)，只使用了常数级别的额外空间

搜索过程示例：

矩阵：
[1,  4,  7,  11, 15]
[2,  5,  8,  12, 19]
[3,  6,  9,  16, 22]
[10, 13, 14, 17, 24]
[18, 21, 23, 26, 30]搜索目标：5步骤：
1. (0,4)=15 > 5 → 左移 → (0,3)
2. (0,3)=11 > 5 → 左移 → (0,2)
3. (0,2)=7 > 5 → 左移 → (0,1)
4. (0,1)=4 < 5 → 下移 → (1,1)
5. (1,1)=5 == 5 → 找到！

代码

golang

func searchMatrix(matrix [][]int, target int) bool {// 防御性编程：处理空矩阵或空行的情况// 如果矩阵为空或第一行为空，直接返回falseif len(matrix) == 0 || len(matrix[0]) == 0 {return false}// 初始化搜索指针// startRow: 当前行索引，从第0行开始// startCol: 当前列索引，从最后一列开始（右上角）startRow := 0startCol := len(matrix[0]) - 1// 搜索循环：确保指针在矩阵有效范围内// startCol >= 0: 列索引不能为负数// startRow < len(matrix): 行索引不能超过矩阵行数for startCol >= 0 && startRow < len(matrix) {// 获取当前指针位置的元素值currentValue := matrix[startRow][startCol]// 找到目标值，直接返回trueif currentValue == target {return true} // 当前值小于目标值，需要找更大的值// 由于矩阵每列从上到下递增，向下移动会找到更大的值else if currentValue < target {startRow++ // 向下移动一行} // 当前值大于目标值，需要找更小的值// 由于矩阵每行从左到右递增，向左移动会找到更小的值else {startCol-- // 向左移动一列}}// 如果循环结束仍未找到目标值，返回falsereturn false
}

// 依旧
func searchMatrix(matrix [][]int, target int) bool {if len(matrix) == 0 || len(matrix[0]) == 0 {return false}row, col := 0, len(matrix[0])-1for row < len(matrix) && col >=0 {if matrix[row][col] == target {return true}else if matrix[row][col] < target {row++}else if matrix[row][col] > target {col--}}return false
}

知识点

这两道都绕，没什么知识点。