矩阵的秩几何含义

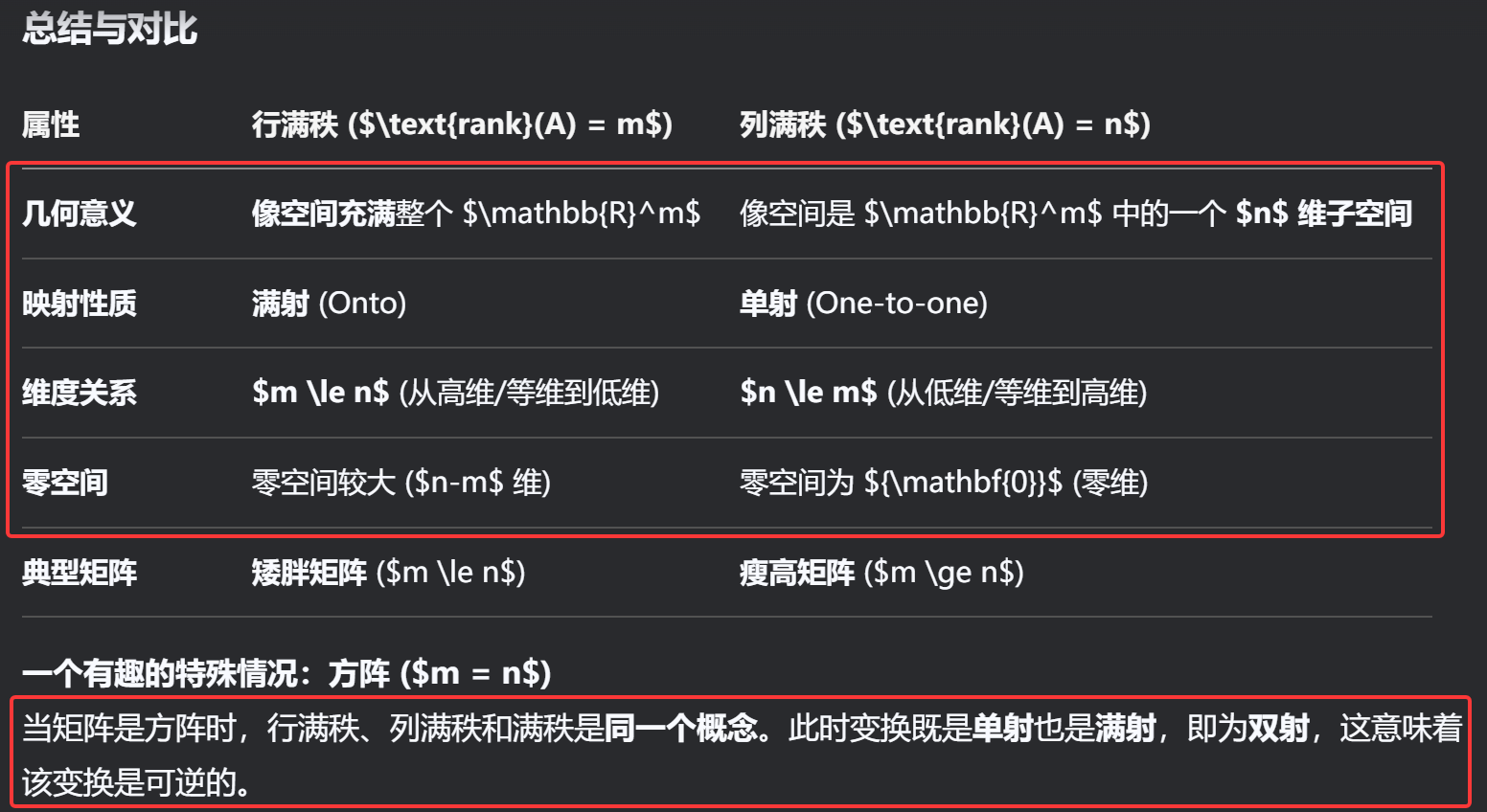
行满秩列满秩的几何意义，秩表示经过矩阵A变换后像空间（列向量）的实际维度。

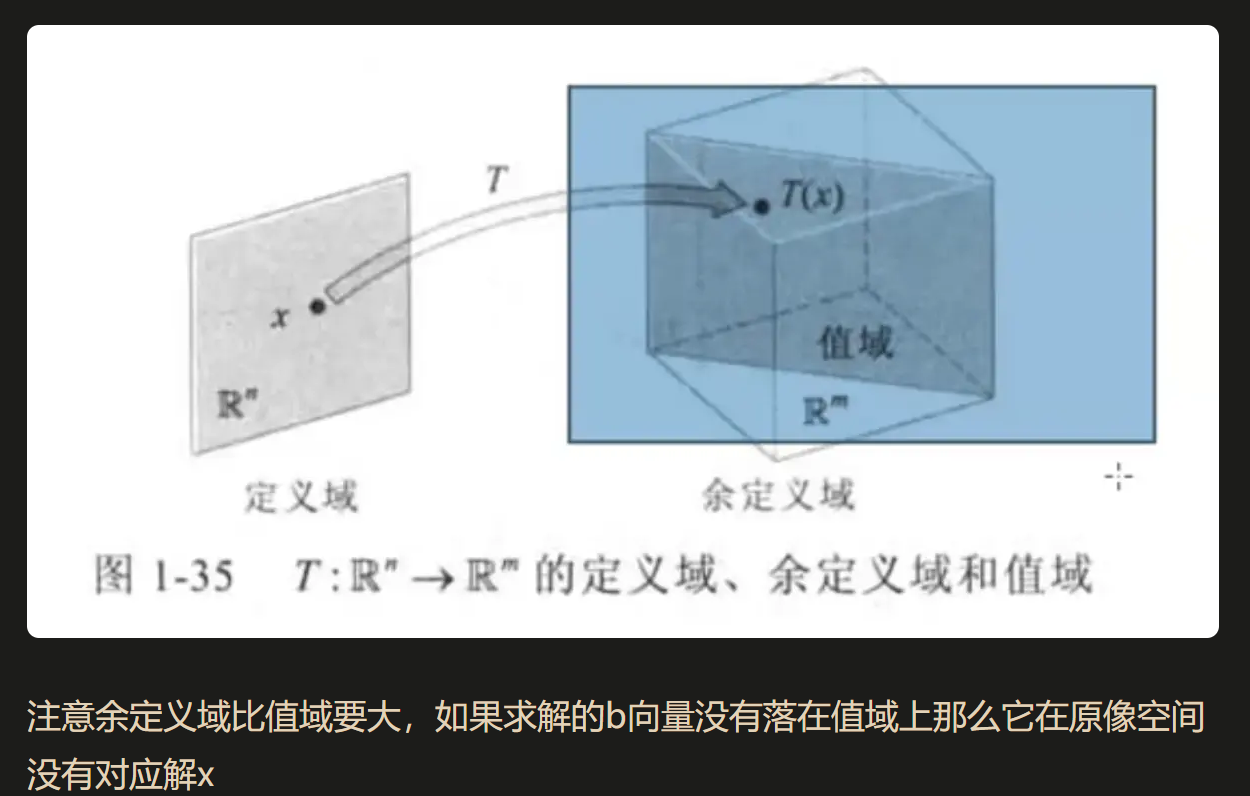
对于一个超定系统A（m>n）,由低维输入向高维空间转换，不发生维度的丢失，即像空间是余定义域（m维空间）的一个n维（原像空间维度）子空间，这种情况下是单射的，即一个输入对应一个唯一输出，它的齐次解空间（又称零空间或核空间）是0维的，即只有0向量一个点

对于一个欠定系统A(m<n)，由高维输入向低维空间转换，变换后原像空间维度就被压缩到m维，即满射，即像空间任意一点都有对应的原像空间的某些（多对一的）输入，因是从高维空间到低维空间的转换，必定存在维度的丢失，故零空间是一个n-m维的空间

对于方阵A（m=n），若A满秩，则它既是单射也是满射即双射（像空间任意一点在原像空间都有唯一输入与之对应）