算法题打卡力扣第209题：长度最小的子数组(mid)

1、题目描述

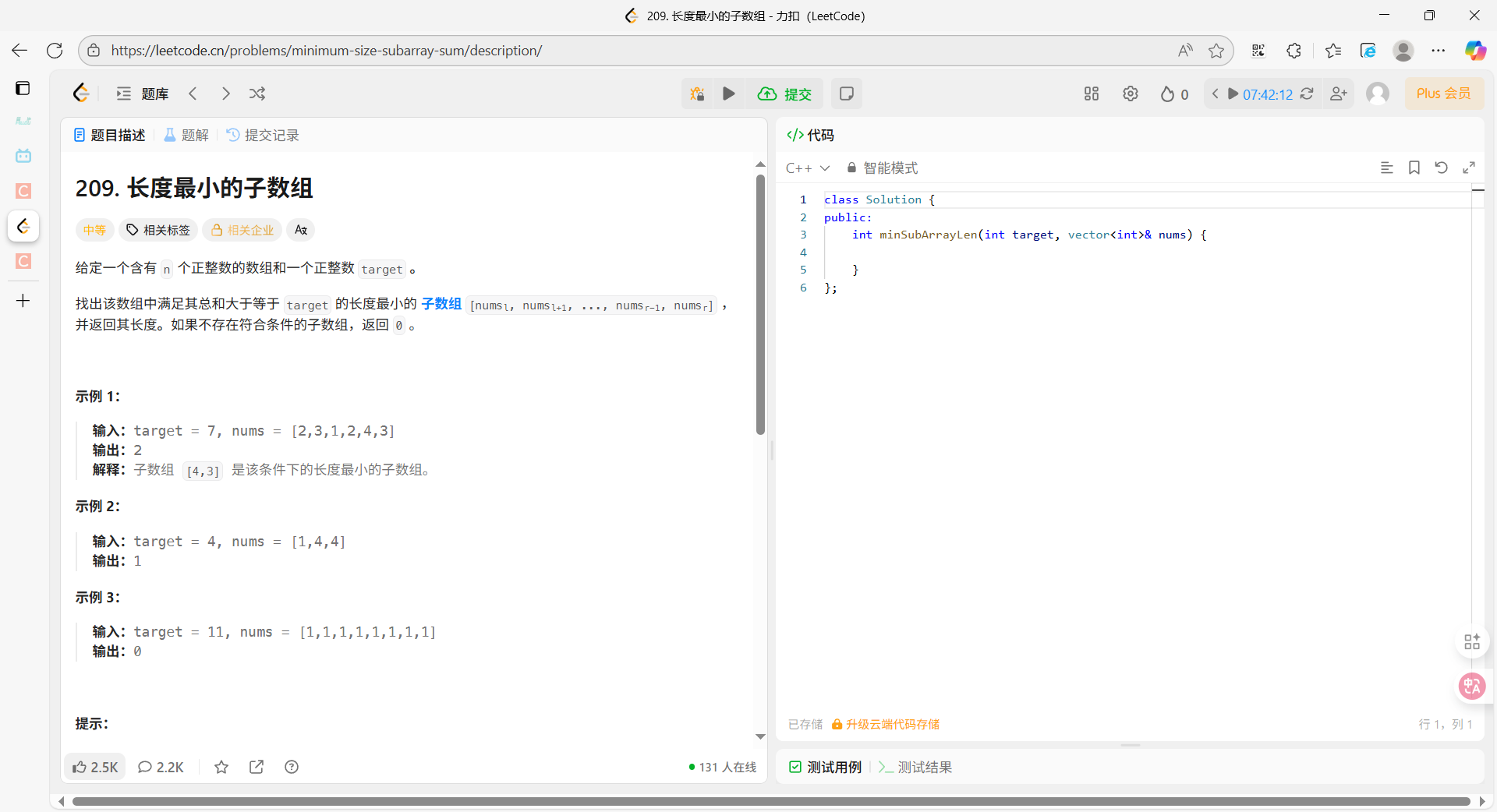
提示：

1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 104

2、解法一：暴力解

思想：
枚举所有数组，计算它们的和，然后找到满足条件的长度最小的那个。
具体步骤：
使用一个外层循环 i 从 0 到 n-1，它代表子数组的起始位置。
在 i 的内部，使用一个内层循环 j 从 i 到 n-1，它代表子数组的结束位置。
对于每一个由 (i, j) 构成的子数组，我们再用一个循环（或在 j 循环中累加）计算从 nums[i] 到 nums[j] 的和 sum。
如果 sum >= target，我们就找到了一个满足条件的子数组。它的长度是 j - i + 1。我们用一个变量 min_len (初始化为无穷大) 来记录和更新遇到的最小长度。
所有循环结束后，如果 min_len 仍然是无穷大，说明没有找到任何满足条件的子数组，返回 0。否则，返回 min_len。

代码

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int n = nums.size();int min_len=0x3f3f3f3f;for(int i=0;i<n;i++){for(int j=i;j<n;j++){int sum=0;for(int k=i;k<=j;k++){sum += nums[k];}if(sum>=target){int len=j-i+1;if(len<min_len){min_len=len;}}}}if(min_len==0x3f3f3f3f){return 0;}else{return min_len;}}
};

执行结果：

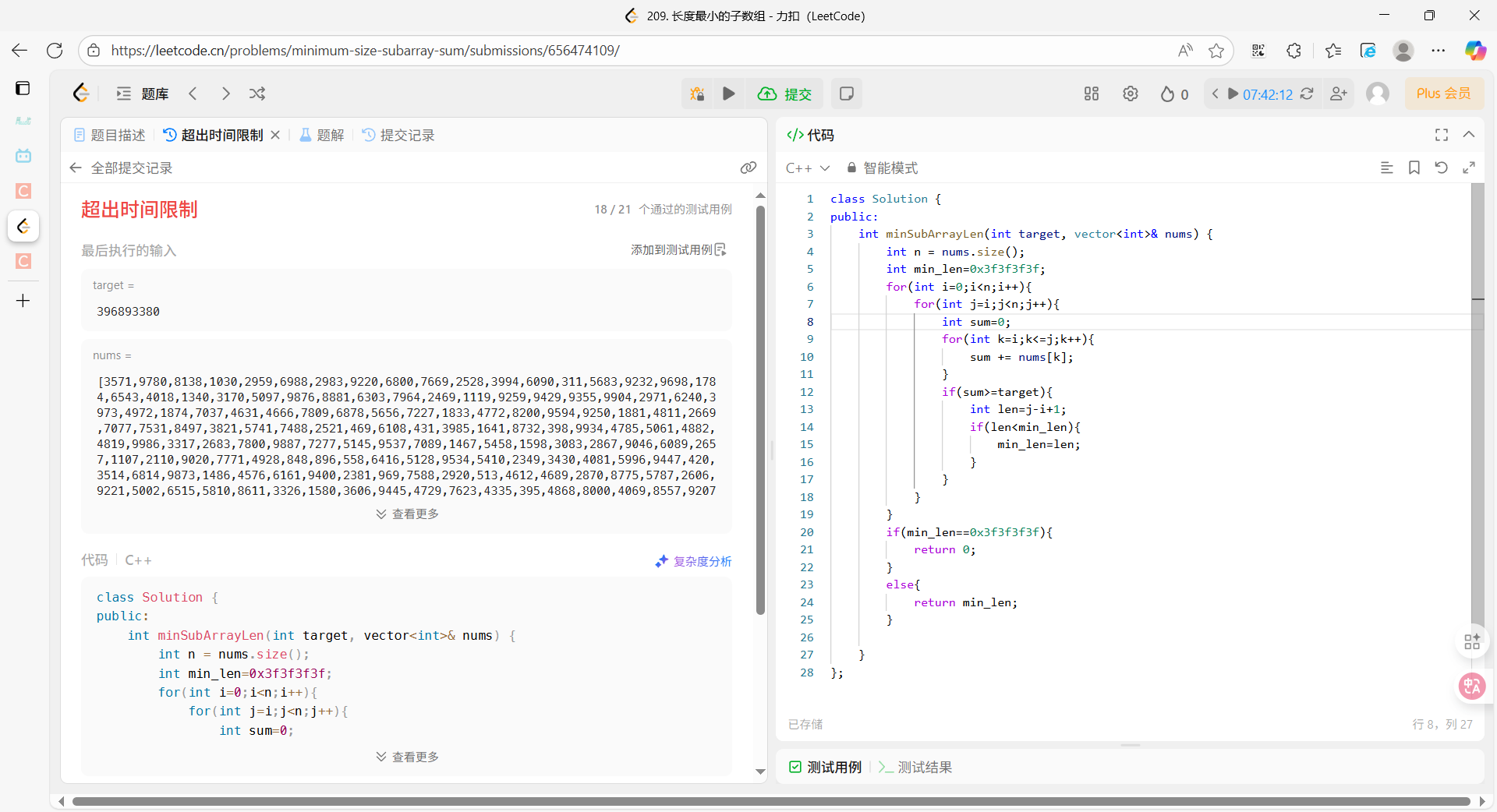
复杂度分析：
时间：O(n^3)
空间：O(1)
优化到时间复杂度为O(n^2),不要每次都用 k 循环重新计算 sum,代码如下：

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int n = nums.size();int min_len=0x3f3f3f3f;for(int i=0;i<n;i++){int sum=0;for(int j=i;j<n;j++){sum += nums[j];if(sum>=target){int len=j-i+1;if(len<min_len){min_len=len;}}}}if(min_len==0x3f3f3f3f){return 0;}else{return min_len;}}
};

依然过不了ε=(´ο｀*)))唉

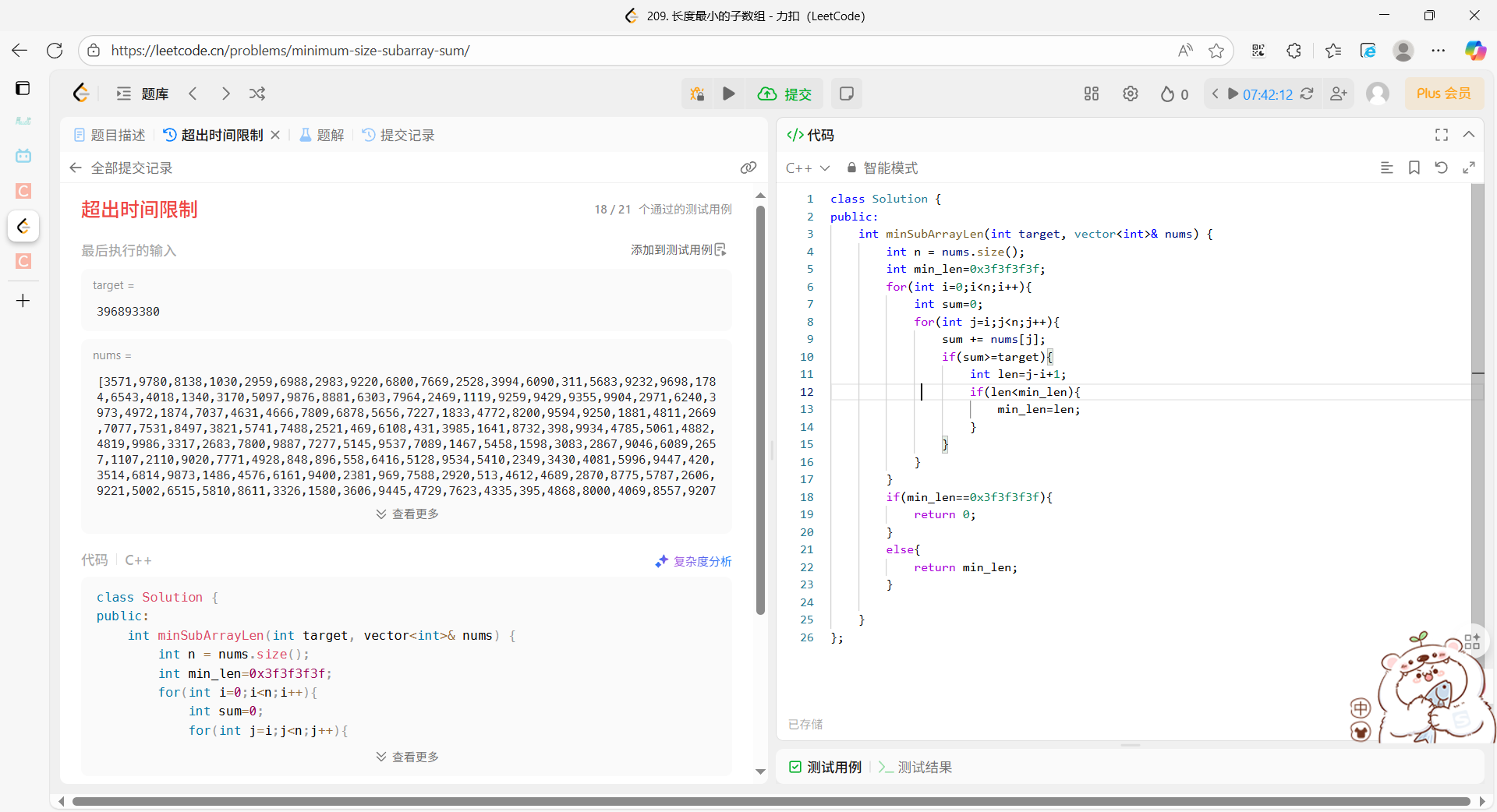
请教g老师

3、解法二：滑动窗口法

g老师：既然暴力解法存在大量重复计算（例如，计算 [i, j] 的和与 [i, j+1] 的和时，[i, j] 部分被重复计算了），我们就需要一种更高效的方法。滑动窗口就是为此而生的。

核心思想：
我们维护一个“窗口”，它代表一个连续的子数组。我们通过移动窗口的左右边界来动态地调整这个子数组，以寻找满足条件的最小长度。
窗口的扩大：不断地将窗口的右边界向右移动，将新的元素包含进窗口，并累加它们的和。
窗口的收缩：一旦窗口内的元素和 sum 大于等于 target，我们就找到了一个可行解。此时，我们会尝试缩小这个窗口，看看能否在仍然满足 sum >= target 的前提下，得到一个更短的长度。我们通过移动窗口的左边界向右来实现收缩。

具体步骤：
初始化两个指针：start = 0 (窗口的左边界) 和 end = 0 (窗口的右边界)。
初始化 current_sum = 0 (当前窗口内元素的和) 和 min_len = infinity (最小长度)。
使用 end 指针作为主循环，从 0 遍历到 n-1。在循环中：
a. 扩大窗口：将 nums[end] 加入到 current_sum 中。 current_sum += nums[end]。
b. 检查并收缩窗口：进入一个 while 循环，条件是 current_sum >= target。
i. 我们找到了一个满足条件的窗口，其长度为 end - start + 1。更新 min_len = min(min_len, end - start + 1)。
ii. 尝试收缩窗口：将窗口最左边的元素 nums[start] 从 current_sum 中减去，current_sum -= nums[start]。
iii. 将左边界 start 向右移动一位，start++。
iv. while 循环会持续进行，直到 current_sum 不再满足 >= target 的条件，说明窗口已经收缩到极限了。
c. end 指针继续向右移动 end++，扩大窗口，寻找下一个可能满足条件的窗口。
主循环结束后，如果 min_len 仍然是无穷大，返回 0，否则返回 min_len。

代码

class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int n = nums.size();if(n==0){return 0;}int min_len = std::numeric_limits<int>::max();int start = 0;long long current_sum = 0;for(int end = 0;end < n;++end){current_sum += nums[end];while(current_sum>=target){min_len = std::min(min_len,end-start+1);current_sum -= nums[start];start++;}}return (min_len == std::numeric_limits<int>::max())?0:min_len;}
};

执行结果：

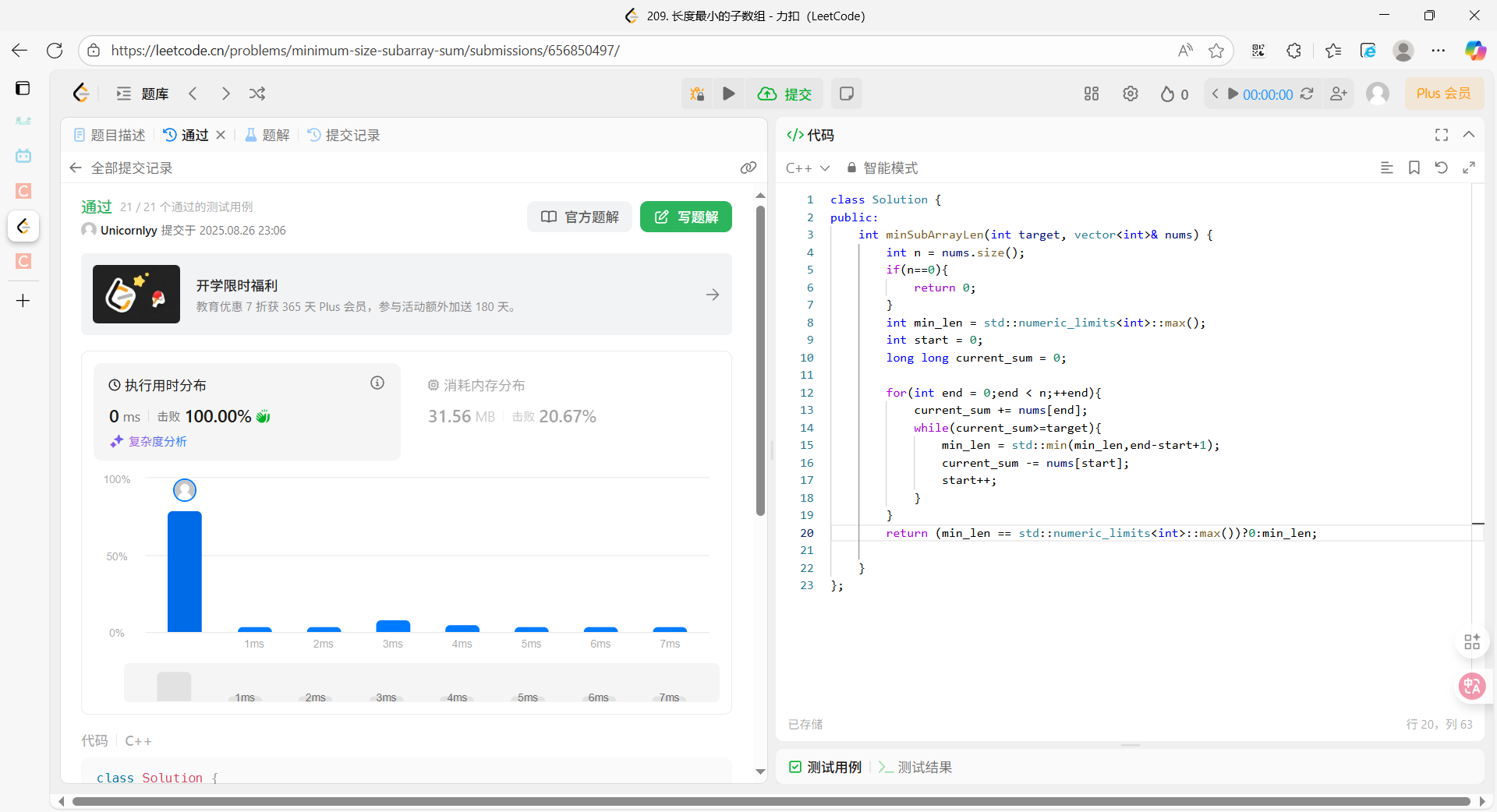
复杂度分析：
时间：O(n)
空间O（1）