【贪心】11 盛最多水的容器（双指针解法）

11 盛最多水的容器（双指针解法）

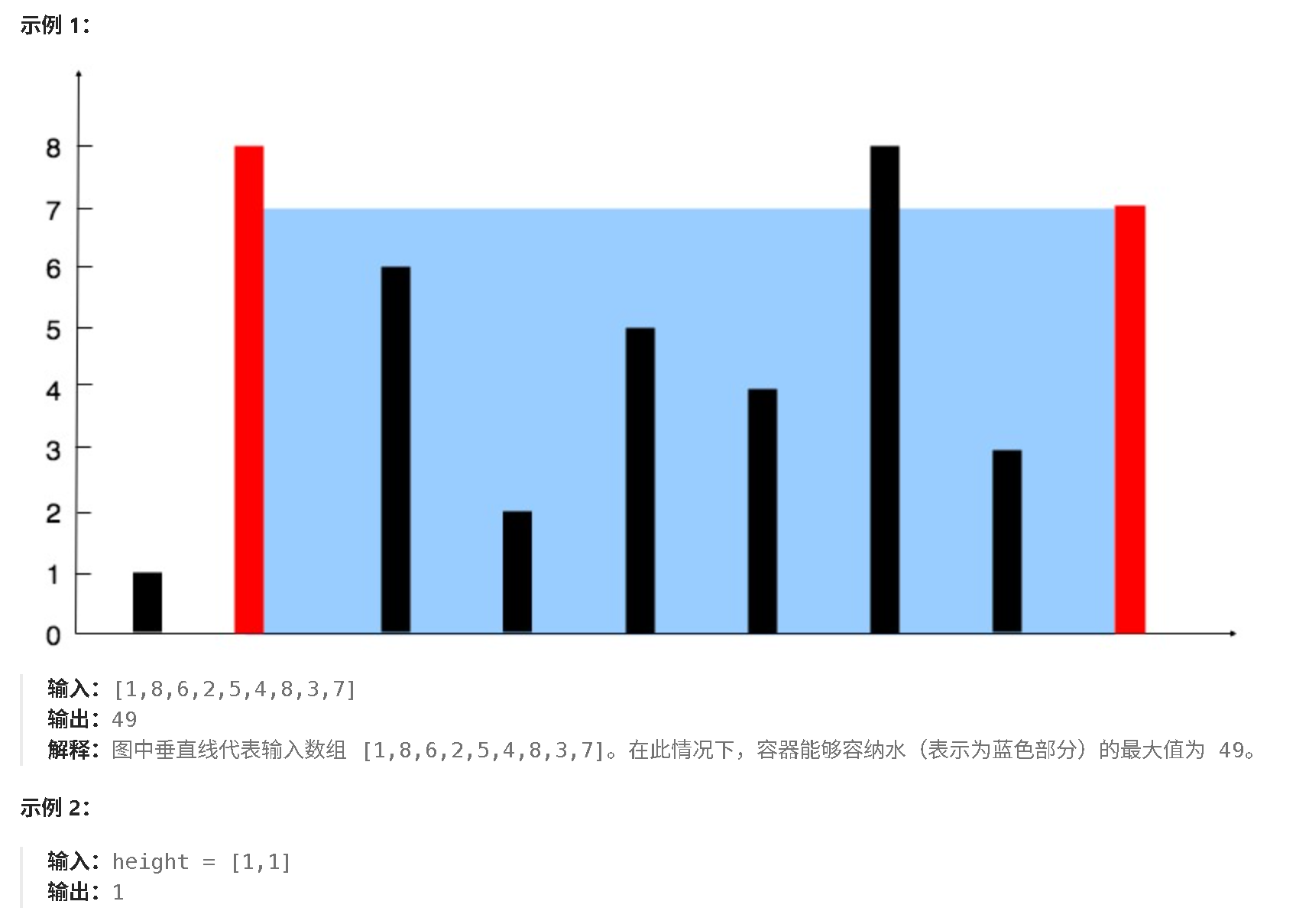
这是一个经典的双指针问题。关键思路是：容器的水量由两个因素决定：

1. 宽度：两条垂线的距离
2. 高度：两条垂线中较短的那条
   

提示：n == height.length
2 <= n <= 105
0 <= height[i] <= 104

解题思路

使用双指针法从两端向中间移动，每次移动高度较小的那个指针：

• 如果移动较高的指针，水位不会上升（受限于较低的那条）
• 如果移动较低的指针，虽然宽度减小，但有可能找到更高的边从而增加水量

def maxArea(height):""":type height: List[int]:rtype: int"""left = 0right = len(height) - 1max_water = 0while left < right:# 计算当前容器的水量h = min(height[left], height[right])w = right - leftmax_water = max(max_water, h * w)# 移动较短的那条线if height[left] < height[right]:left += 1else:right -= 1return max_water

时间复杂度分析

• 时间复杂度：O(n)，其中n是数组长度，只需要遍历一次数组
• 空间复杂度：O(1)，只使用了常数级别的额外空间

这种贪心策略可以保证找到最优解，因为我们总是尝试保留可能产生更大容量的边。

代码

def maxArea(height):""":type height: List[int]:rtype: int"""left = 0right = len(height) - 1max_water = 0while left < right:# 计算当前容器的水量h = min(height[left], height[right])w = right - leftmax_water = max(max_water, h * w)# 移动较短的那条线if height[left] < height[right]:left += 1else:right -= 1return max_water# 给出盛最多水的容器的算法实现，双指针法。添加详细注释
def maxAreaDetailed(height):"""计算盛最多水的容器的最大面积:param height: 列表，表示每个位置的高度:return: 最大面积"""left = 0  # 左指针，初始位置在列表的开头right = len(height) - 1  # 右指针，初始位置在列表的末尾max_water = 0  # 初始化最大面积为0# 当左指针小于右指针时，继续计算面积while left < right:# 计算当前容器的高度和宽度h = min(height[left], height[right])  # 容器的高度由较短的那条线决定w = right - left  # 容器的宽度是左右指针之间的距离max_water = max(max_water, h * w)  # 更新最大面积# 移动较短的那条线，以期望找到更大的面积if height[left] < height[right]:left += 1  # 左指针右移，尝试找到更高的左边界else:right -= 1  # 右指针左移，尝试找到更高的右边界return max_water  # 返回计算得到的最大面积# 给出盛最多水的容器的算法实现，双指针法。添加详细注释，重新实现maxArea方法
class Solution:def maxArea(self, height):"""计算盛最多水的容器的最大面积:param height: 列表，表示每个位置的高度:return: 最大面积"""left = 0  # 左指针，初始位置在列表的开头right = len(height) - 1  # 右指针，初始位置在列表的末尾max_water = 0  # 初始化最大面积为0# 当左指针小于右指针时，继续计算面积while left < right:# 计算当前容器的高度和宽度h = min(height[left], height[right])  # 容器的高度由较短的那条线决定w = right - left  # 容器的宽度是左右指针之间的距离max_water = max(max_water, h * w)  # 更新最大面积# 移动较短的那条线，以期望找到更大的面积if height[left] < height[right]:left += 1  # 左指针右移，尝试找到更高的左边界else:right -= 1  # 右指针左移，尝试找到更高的右边界return max_water  # 返回计算得到的最大面积# 示例用法
heights = [1,8,6,2,5,4,8,3,7]
print("最大面积:", maxAreaDetailed(heights))  # 输出: 最大面积: 49
solution = Solution()
print("最大面积 (类方法):", solution.maxArea(heights))  # 输出: 最大面积 (类方法): 49

two-pointer technique

The two-pointer technique is a common algorithmic approach used to solve problems involving arrays or lists. It involves using two pointers (or indices) that traverse the array from different directions. Here’s how it works in the context of the “Container With Most Water” problem:

Key Idea

The goal is to maximize the area of water that can be contained between two lines. The area is determined by:

• Height: The shorter of the two lines at the current pointers.
• Width: The distance between the two pointers.

Steps

1. Initialize Pointers:

   • Place one pointer (left) at the beginning of the array.
   • Place the other pointer (right) at the end of the array.

2. Calculate Area:

   • Compute the area using the formula: area = min(height[left], height[right]) * (right - left).

3. Update Maximum Area:

   • Keep track of the maximum area encountered so far.

4. Move the Pointer with the Smaller Height:

   • If height[left] < height[right], increment the left pointer to potentially find a taller line.
   • Otherwise, decrement the right pointer to potentially find a taller line.
   • This ensures that the width decreases, but the height might increase, potentially leading to a larger area.

5. Repeat:

   • Continue until the two pointers meet.

Why It Works

The two-pointer technique works because:

• The width decreases as the pointers move inward, so the only way to increase the area is by finding a taller line.
• By always moving the pointer pointing to the shorter line, you maximize the chance of increasing the height.

This approach ensures that all possible pairs of lines are considered efficiently, without needing to check every combination explicitly. The time complexity is O(n).

双指针技术详解

双指针技术是一种常用的数组/链表处理方法，通过两个指针从不同位置或方向遍历数据结构，有效减少时间复杂度。在"盛最多水的容器"问题中：

双指针的工作原理

1. 初始化：左指针在数组开头，右指针在数组末尾

2. 计算面积：面积 = min(height[left], height[right]) × (right - left)

3. 移动策略：

   • 总是移动高度较小的那个指针
   • 因为如果移动较高的指针，新容器的高度仍受限于较低的边，而宽度减小，面积只会更小
   • 移动较低的指针可能找到更高的边，有机会增加面积

4. 终止条件：左右指针相遇时停止

为什么这样工作？

• 随着指针移动，宽度必然减小
• 只有找到更高的边才可能增加面积
• 移动高度较低的指针是唯一可能增加面积的选择

更多双指针算法示例

1. 有序数组的两数之和

def twoSum(numbers, target):left, right = 0, len(numbers) - 1while left < right:current_sum = numbers[left] + numbers[right]if current_sum == target:return [left + 1, right + 1]  # 题目要求索引从1开始elif current_sum < target:left += 1  # 和太小，增加左边的数else:right -= 1  # 和太大，减小右边的数return [-1, -1]  # 没有找到答案

2. 删除有序数组中的重复项

def removeDuplicates(nums):if not nums:return 0slow = 0  # 慢指针指向处理好的数组的最后一个位置for fast in range(1, len(nums)):  # 快指针遍历数组if nums[fast] != nums[slow]:slow += 1nums[slow] = nums[fast]return slow + 1  # 返回新数组的长度

3. 验证回文串

def isPalindrome(s):left, right = 0, len(s) - 1while left < right:# 跳过非字母数字字符while left < right and not s[left].isalnum():left += 1while left < right and not s[right].isalnum():right -= 1# 比较(忽略大小写)if s[left].lower() != s[right].lower():return Falseleft += 1right -= 1return True

4. 三数之和

def threeSum(nums):result = []nums.sort()for i in range(len(nums) - 2):# 跳过重复值if i > 0 and nums[i] == nums[i-1]:continueleft, right = i + 1, len(nums) - 1while left < right:sum = nums[i] + nums[left] + nums[right]if sum < 0:left += 1elif sum > 0:right -= 1else:result.append([nums[i], nums[left], nums[right]])# 跳过重复值while left < right and nums[left] == nums[left+1]:left += 1while left < right and nums[right] == nums[right-1]:right -= 1left += 1right -= 1return result

双指针技术是解决数组相关问题的强大工具，特别适合需要找到特定组合或模式的场景，往往能将暴力解法的O(n²)优化至O(n)。

---

为什么盛最多水的容器使用贪心算法

这个问题适合用贪心算法是因为在每一步决策中，我们都采取了"局部最优"的选择（移动较短的那条线），期望最终达到"全局最优"（最大容积）。

贪心策略分析

1. 决策原则：每次移动高度较短的那条线

   • 如果移动较高的线，新容器的高度仍受限于较短线，而宽度减小，容积必然减小
   • 只有移动较短的线，才有可能找到更高的线，从而增加容积

2. 贪心特性：

   • 局部最优：每次移动决策都基于当前状态做出最优选择
   • 不回溯：一旦做出决策，不会重新考虑之前的选择
   • 最终最优：这种策略能保证找到全局最优解

为什么不需要尝试所有组合？

在朴素解法中，我们需要O(n²)复杂度来检查所有线对。但双指针贪心方法证明：

• 最大面积容器的两条边必定是通过我们的贪心移动策略找到的
• 因为任何被跳过的组合，都无法形成比我们找到的更大的容器

其他双指针问题示例

1. 三数之和（求和为零）

def threeSum(nums):res = []nums.sort()for i in range(len(nums)-2):if i > 0 and nums[i] == nums[i-1]:continueleft, right = i+1, len(nums)-1while left < right:sum_val = nums[i] + nums[left] + nums[right]if sum_val < 0:left += 1elif sum_val > 0:right -= 1else:res.append([nums[i], nums[left], nums[right]])while left < right and nums[left] == nums[left+1]:left += 1while left < right and nums[right] == nums[right-1]:right -= 1left += 1right -= 1return res

2. 合并两个有序数组

def merge(nums1, m, nums2, n):p1 = m - 1  # nums1 有效元素尾指针p2 = n - 1  # nums2 尾指针p = m + n - 1  # 合并结果尾指针while p1 >= 0 and p2 >= 0:if nums1[p1] > nums2[p2]:nums1[p] = nums1[p1]p1 -= 1else:nums1[p] = nums2[p2]p2 -= 1p -= 1# 如果p2还有剩余元素while p2 >= 0:nums1[p] = nums2[p2]p2 -= 1p -= 1

3. 快慢指针：判断链表是否有环

def hasCycle(head):if not head or not head.next:return Falseslow = headfast = head.nextwhile slow != fast:if not fast or not fast.next:return Falseslow = slow.nextfast = fast.next.nextreturn True

4. 滑动窗口：最小覆盖子串

def minWindow(s, t):need = {}for c in t:need[c] = need.get(c, 0) + 1left = 0right = 0valid = 0window = {}min_len = float('inf')start = 0while right < len(s):c = s[right]right += 1if c in need:window[c] = window.get(c, 0) + 1if window[c] == need[c]:valid += 1while valid == len(need):if right - left < min_len:start = leftmin_len = right - leftd = s[left]left += 1if d in need:if window[d] == need[d]:valid -= 1window[d] -= 1return "" if min_len == float('inf') else s[start:start+min_len]

双指针技术是一种既高效又灵活的解题思路，能将许多看似复杂的问题简化为线性时间复杂度的解决方案。