【文献阅读】SparseGPT: Massive Language Models Can be Accurately Pruned in One-Shot
ICML, 2023
摘要
我们首次证明,大规模生成式预训练 Transformer(GPT)系列模型可通过一次性剪枝达到至少 50% 的稀疏度,且无需任何重训练,精度损失极小。这一成果通过一种名为 SparseGPT 的新型剪枝方法实现,该方法专为在大规模 GPT 系列模型上高效且精准地工作而设计。我们可在 4.5 小时内对最大的开源模型 OPT-175B 和 BLOOM-176B 执行 SparseGPT 剪枝,且能在困惑度增加可忽略不计的情况下实现 60% 的非结构化稀疏度:值得注意的是,这些模型中超过 1000 亿个权重在推理时可被忽略。SparseGPT 适用于半结构化(2:4 和 4:8)模式,且与权重量化方法兼容。代码可在以下地址获取:https://github.com/IST-DASLab/sparsegpt1。
1. 引言
来自生成式预训练 Transformer(GPT)家族的大型语言模型(LLMs)在众多任务中展现出卓越性能,但因其庞大的规模和计算成本,部署难度较大。例如,性能顶尖的 GPT-175B 模型拥有 1750 亿个参数,在半精度(FP16)格式下存储总量至少为 320GB(按 1024 的倍数计算),这导致其推理至少需要 5 块配备 80GB 内存的 A100 GPU。因此,通过模型压缩降低这些成本自然引起了广泛关注。迄今为止,几乎所有现有的 GPT 压缩方法都集中在量化上(Dettmers 等人,2022;Yao 等人,2022;Xiao 等人,2022;Frantar 等人,2022a),即降低模型数值表示的精度2。
另一种互补的压缩方法是剪枝,它移除网络元素,从单个权重(非结构化剪枝)到更高粒度的结构,如权重矩阵的行 / 列(结构化剪枝)。剪枝有着悠久的历史(LeCun 等人,1989;Hassibi 等人,1993),并已成功应用于视觉模型和小规模语言模型(Hoefler 等人,2021)。然而,性能最佳的剪枝方法需要对模型进行大量重训练才能恢复精度。反过来,这对于 GPT 规模的模型来说成本极高。虽然存在一些精确的一次性剪枝方法(Hubara 等人,2021a;Frantar 等人,2022b),无需重训练即可压缩模型,但不幸的是,当应用于数十亿参数的模型时,这些方法的成本也变得非常高昂。因此,迄今为止,关于十亿参数级模型的精确剪枝几乎没有相关研究3。
概述
在本文中,我们提出了 SparseGPT,这是第一种能在 100 - 1000 多亿参数规模的模型上高效工作的精确一次性剪枝方法。SparseGPT 通过将剪枝问题转化为一系列超大规模的稀疏回归实例来实现剪枝。然后,它通过一种新的近似稀疏回归求解器来解决这些实例,该求解器效率极高,可在单个 GPU 上在几小时内对最大的开源 GPT 模型(1750 亿参数)执行剪枝。同时,SparseGPT 的精度足够高,剪枝后无需任何微调,精度损失可忽略不计。例如,当在最大的公开可用生成式语言模型(OPT - 175B 和 BLOOM - 176B)上执行时,SparseGPT 可一次性实现 50%-60% 的稀疏度,且无论是通过困惑度还是零样本精度衡量,精度损失都很小4。
我们的实验(图 1 和图 2 展示了部分结果)得出以下结论。首先,如图 1 所示,SparseGPT 可在例如 OPT 家族的 1750 亿参数变体(Zhang 等人,2022)中实现高达 60% 的均匀层稀疏度,且精度损失极小。相比之下,唯一已知的可轻松扩展到该规模的一次性基线方法 —— 幅度剪枝(Hagiwara,1994;Han 等人,2015)仅能在 10% 的稀疏度下保持精度,超过 30% 的稀疏度后精度则完全崩溃。
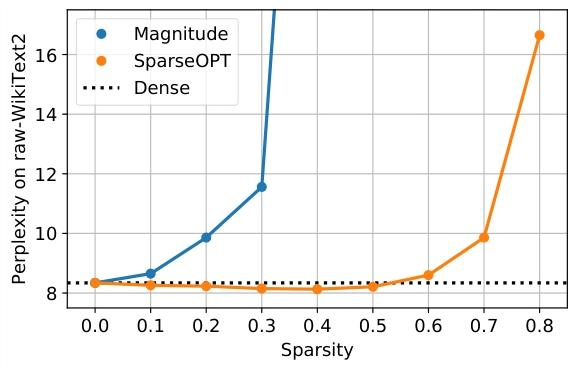
图 1. 在 OPT-175B 上,SparseGPT 与幅度剪枝在不同均匀每层稀疏度下的稀疏度 - 困惑度对比7。
其次,如图 2 所示,SparseGPT 还能在更严格但硬件友好的 2:4 和 4:8 半结构化稀疏模式(Mishra 等人,2021)中精确地施加稀疏度,尽管对于较小的模型,其精度相对于密集基线会有所损失5。
一个关键的积极发现(如图 2 所示)是,更大的模型更容易压缩:在固定的稀疏度下,相对于较小的模型,更大的模型精度下降明显更少。(例如,OPT 和 BLOOM 家族中最大的模型可以被稀疏化到 50%,而困惑度几乎没有增加。)此外,我们的方法允许将稀疏度与权重量化技术相结合(Frantar 等人,2022a):例如,我们可以在 OPT-175B 上实现 50% 的权重稀疏度与 4 位权重量化,且困惑度增加可忽略不计6。
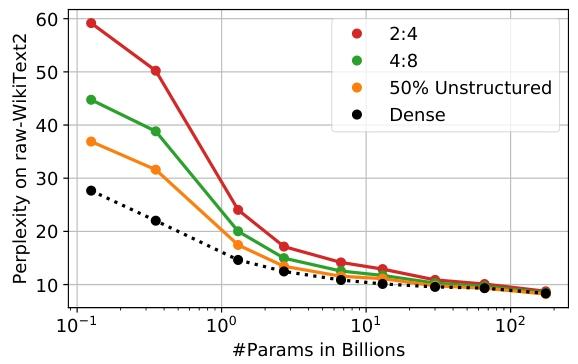
图2. 使用SparseGPT将整个OPT模型家族(1.35亿、3.5亿……660亿、1750亿参数)压缩为不同稀疏模式时的困惑度与模型及稀疏类型关系图。
SparseGPT 的一个显著特性是它完全是局部的,即它仅依赖于旨在保持每层输入 - 输出关系的权重更新,这些更新的计算无需任何全局梯度信息。因此,我们发现能够直接在密集预训练模型的 “邻域” 中识别出此类稀疏模型,其输出与密集模型的输出高度相关,这一点非常值得关注8。
2. 背景
训练后剪枝是一种实际场景,给定一个优化良好的模型 θ以及一些校准数据,我们必须获得 θ的压缩版本(例如,稀疏和 / 或量化版本)。该场景最初在量化领域得到普及(Hubara 等人,2021b;Nagel 等人,2020;Li 等人,2021),最近也成功扩展到剪枝领域(Hubara 等人,2021a;Frantar 等人,2022b;Kwon 等人,2022)9。
逐层剪枝
训练后压缩通常通过将全模型压缩问题分解为逐层子问题来实现,子问题的求解质量通过给定输入 xₗ时,未压缩层(权重为 wₗ)与压缩层的输出之间的ℓ₂误差来衡量。具体而言,对于剪枝,(Hubara 等人,2021a)将该问题表述为:对于每层ℓ,找到具有特定目标密度的稀疏掩码 Mₗ,以及可能更新的权重ŵₗ,使得
\(\widehat{w}_{\ell}\) such that \[argmin_{mask M_{\ell}, \overline{W}_{\ell}}\left\| W_{\ell} X_{\ell}-\left(M_{\ell} \odot \hat{W}_{\ell}\right) X_{\ell}\right\| _{2}^{2} . (1)\]
整体压缩模型随后通过将各个压缩层 “拼接” 在一起获得12。
掩码选择与权重重构
式(1)中逐层剪枝问题的一个关键方面是,掩码 Mₗ和剩余权重Ŵₗ是联合优化的,这使得该问题成为 NP 难问题(Blumensath & Davies,2008)。因此,精确求解较大层的问题是不现实的,导致所有现有方法都采用近似方法13。
一种特别流行的方法是将问题分为掩码选择和权重重构(He 等人,2018;Kwon 等人,2022;Hubara 等人,2021a)。具体而言,这意味着首先根据某种显著性标准(如权重幅度)选择剪枝掩码 M(Zhu & Gupta,2017),然后在保持掩码不变的情况下优化剩余未剪枝的权重。重要的是,一旦掩码固定,式(1)就变成了易于优化的线性平方误差问题14。
现有求解器
早期工作(Kingdon,1997)将迭代线性回归应用于小型网络。最近,AdaPrune 方法(Hubara 等人,2021a)通过基于幅度的权重选择,然后应用 SGD 步骤重构剩余权重,在现代模型上取得了良好的结果。
后续工作表明,通过消除掩码选择和权重重构之间的严格分离,可以进一步提高剪枝精度。迭代 AdaPrune(Frantar & Alistarh,2022)通过逐步剪枝并在中间进行重新优化来执行剪枝,而 OBC(Frantar 等人,2022b)引入了一种贪心求解器,每次移除一个权重,并在每次迭代后通过高效的闭式方程完全重构剩余权重15。
扩展到 1000 多亿参数的难度
现有的训练后技术都是为了精确压缩参数规模达数亿的模型而设计的,计算时间从几分钟到几小时不等。然而,我们的目标是对规模大 1000 倍的模型进行稀疏化16。
即使是针对理想速度 / 精度权衡进行优化的 AdaPrune 方法,稀疏化仅 13 亿参数的模型也需要几个小时(另见第 4 节),按线性扩展计算,稀疏化 1750 亿参数的 Transformer 模型则需要几百小时(几周)。更精确的方法至少比 AdaPrune 昂贵几倍(Frantar & Alistarh,2022),甚至扩展性比线性更差(Frantar 等人,2022b)。
这表明,将现有的精确训练后技术扩展到超大型模型是一项具有挑战性的工作。因此,我们提出了一种新的逐层求解器 SparseGPT,它基于对闭式方程的仔细近似,在运行时间和精度方面都能轻松扩展到巨型模型17。
3. SparseGPT 算法
3.1 快速近似重构
动机
如第 2 节所述,对于固定的剪枝掩码 M,掩码中所有权重的最优值可以通过求解每个矩阵行 wⁱ对应的稀疏重构问题精确计算:
wMii=(XMiXMi⊤)−1XMi(wMiXMi)⊤(2),
其中 X_{Mᵢ} 仅表示其对应权重在第 i 行中未被剪枝的输入特征子集,w_{Mᵢ} 表示它们各自的权重。然而,这需要对第 i 行的剪枝掩码 Mᵢ所保留的值对应的 Hessian 矩阵 H_{Mᵢ}=X_{Mᵢ} X_{Mᵢ}^⊤求逆,即计算 (H_{Mᵢ})⁻¹,分别对所有行 1≤i≤dᵣₒᵥ进行。
一次这样的求逆需要 O (dₒₗ³) 时间,因此在 dᵣₒᵥ行上的总计算复杂度为 O (dᵣₒᵥ・dₒₗ³)。对于 Transformer 模型,这意味着整体运行时间与隐藏维度 dₕᵢddₑₙ的 4 次方成正比;我们需要至少将速度提高 dₕᵢddₑₙ倍才能得到实用的算法18 19 20 21。
不同的行 - Hessian 挑战
根据式(2)优化重构未剪枝权重的高计算复杂度主要源于以下事实:求解每行需要单独对一个 O (dₒₗ×dₒₗ) 矩阵求逆。这是因为行掩码 Mᵢ通常不同,且 (H_{Mᵢ})⁻¹≠(H⁻¹) Mᵢ,即掩码 Hessian 的逆不等于完整逆的掩码版本。图 3 也对此进行了说明。如果所有行掩码都相同,那么我们只需要计算一个共享的逆,因为 H=XX⊤仅取决于所有行相同的层输入。
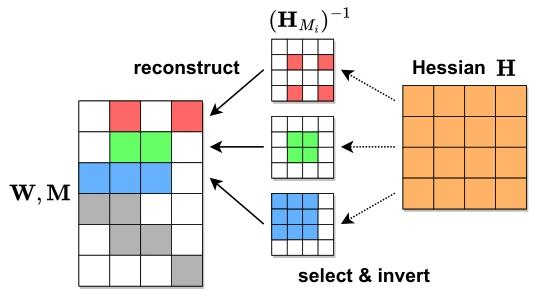
图 3. 行 - Hessian 挑战说明:行被独立稀疏化,剪枝的权重为白色23。
可以在掩码选择中强制执行这样的约束,但这会对最终模型精度产生重大影响,因为对大型结构(如整列)的权重进行稀疏化比单独剪枝它们要困难得多 ²。设计既精确又高效的近似算法的关键在于能够在具有不同剪枝掩码的行之间重用 Hessian 矩阵。我们现在提出一种有原则的方法来实现这一点24。
等效迭代视角
为了激发我们的算法,我们首先必须从不同的迭代角度看待逐行权重重构,使用经典的 OBS 更新(Hassibi 等人,1993;Singh & Alistarh,2020;Frantar 等人,2021)。假设损失函数的二次近似,其中当前权重 w 是最优的,OBS 更新 δₘ提供了剩余权重的最优调整,以补偿索引 m 处权重的移除,并产生误差 εₘ:
δm=−[H−1]mmwm⋅H:,m−1,εm=[H−1]mmwm2(3)。
由于对应于 W 的一行的逐层剪枝的损失函数是二次的,因此在这种情况下 OBS 公式是精确的。因此,w + δₘ是对应于掩码 {m} 的最优权重重构。此外,给定对应于掩码 M 的最优稀疏重构 w⁽ᴹ⁾,我们可以再次应用 OBS 来找到对应于掩码 M'=M - {m} 的最优重构。因此,这意味着不必直接求解完整掩码 M={m₁,…,mₚ}^C,我们可以通过迭代应用 OBS 来依次单独剪枝权重 m₁到 mₚ,将初始完整掩码缩减到 M,并最终得到与直接应用完整 M 的闭式回归重构相同的最优解26。
最优部分更新
应用 OBS 更新 δₘ可能会调整当前掩码 M 中所有可用参数的值,以补偿 wₘ的移除。然而,如果我们只更新剩余未剪枝权重中的子集 U⊆M,会怎样呢?因此,我们仍然可以利用误差补偿,仅使用 U 中的权重,同时降低应用 OBS 的成本27。
这种部分更新确实可以通过简单地使用对应于 U 的 Hessian 矩阵 Hᵤ而不是 Hₘ计算 OBS 更新,并仅更新 wᵤ来实现。重要的是,对于 U,我们特定的逐层问题的损失仍然是二次的,并且 OBS 更新仍然是最优的:
对 U 的限制本身不会带来任何额外的近似误差,只是误差补偿可能不够有效,因为可用于调整的权重更少。同时,如果 | U| < |M|,那么对 Hᵤ求逆将比对 Hₘ求逆快得多。我们现在将利用这种机制来实现我们跨 W 的所有行同步掩码 Hessian 矩阵的目标28。
Hessian 同步
在下面的内容中,假设输入特征 j=1,…,dₒₗ的顺序是固定的。由于这些特征通常是随机排列的,为简单起见,我们将保留给定的顺序,但原则上可以选择任何排列。接下来,我们递归地定义 dₒₗ个索引子集 Uⱼ:
Uj+1=Uj−{j}withU1={1,...,dcol}(4)。
也就是说,从 U₁是所有索引的集合开始,每个子集 Uⱼ₊₁通过从前一个子集 Uⱼ中移除最小的索引来创建。这些子集还对应一系列逆 Hessian 矩阵 (H_{Uⱼ})⁻¹=((XX⊤){Uⱼ})⁻¹,我们将在 W 的所有行之间共享这些矩阵。重要的是,根据(Frantar 等人,2022b),更新后的逆矩阵 (H{Uⱼ₊₁})⁻¹ 可以通过高斯消元的一步,从 B=(H_{Uⱼ})⁻¹ 中移除对应于原始 H 中的 j 的第一行和第一列,以 O (dₒₗ²) 时间高效计算:
(HUj+1)−1=(B−[B]111⋅B:,1B1,:)2:,2:(5),
其中 (H_{U₁})⁻¹=H⁻¹。因此,整个 dₒₗ个逆 Hessian 矩阵序列可以通过递归计算,时间复杂度为 O (dₒₗ³),即与在初始 H⁻¹ 求逆的基础上再进行一次额外的矩阵求逆的成本相似。
一旦某个权重 wₖ被剪枝,它就不应再被更新。此外,当我们剪枝 wₖ时,我们希望更新尽可能多的未剪枝权重,以实现最大程度的误差补偿。这导致了以下策略:依次迭代 Uⱼ及其对应的逆 Hessian 矩阵 (H_{Uⱼ})⁻¹,并对所有行 i,如果 j∉Mᵢ,则剪枝
wⱼ。重要的是,每个逆 Hessian 矩阵 (H_{Uⱼ})⁻¹ 仅计算一次,并在所有行中用于移除属于剪枝掩码的权重 j。算法的可视化如图 4 所示。
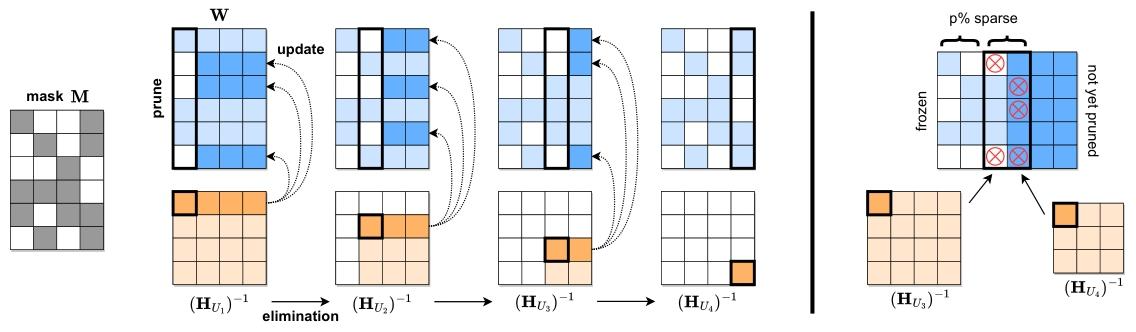
图 4. [左] SparseGPT 重构算法的可视化。给定固定的剪枝掩码 M,我们使用一系列 Hessian 逆矩阵 (H_{Uⱼ})⁻¹ 逐步剪枝权重矩阵 W 的每一列,并更新这些行中位于被处理列 “右侧” 的其余权重。具体而言,被剪枝权重(深蓝色)“右侧” 的权重将被更新以补偿剪枝误差,而非剪枝权重不会产生更新(浅蓝色)。[右] 通过迭代分块进行自适应掩码选择的说明。
这张图展示了 SparseGPT 算法 中关键的 逐层剪枝与权重更新流程,结合 “行 - Hessian 挑战” 和 “自适应掩码选择” 逻辑,拆解核心步骤:
左侧:非结构化剪枝流程(逐列迭代)
-
掩码与矩阵初始化
-
左起第一列是剪枝掩码
M(灰色表示保留权重,白色表示剪枝),右侧是待剪枝的权重矩阵W(蓝色)和对应的 Hessian 逆矩阵(橙色方块标记当前处理列)。
-
-
逐列剪枝 + 部分更新
-
每一轮选一列(黑色框标记)执行剪枝:
-
先 “剪枝(prune)” 该列中需置零的权重(白色方格),再用当前列对应的 Hessian 逆矩阵(如 \((\mathbf{H}_{U_1})^{-1}\))计算 误差补偿,更新未剪枝的权重(蓝色方格的箭头表示更新流向)。
-
剪枝后,Hessian 逆矩阵通过 “消元(elimination)” 更新(如 \((\mathbf{H}_{U_1})^{-1} \to (\mathbf{H}_{U_2})^{-1}\)),为下一列剪枝做准备。
-
-
核心逻辑:用共享的 Hessian 逆矩阵序列,逐列剪枝并更新剩余权重,平衡精度与计算成本。
-
右侧:自适应掩码选择(分块剪枝)
-
展示 “分块(block)” 剪枝逻辑:将权重矩阵按列分块(黑色框),每块内选
p%权重剪枝(红色叉号)。 -
已剪枝的列(
frozen)用固定的 Hessian 逆矩阵(如 \((\mathbf{H}_{U_3})^{-1}\))补偿误差;未剪枝的列(not yet pruned)后续处理,体现 “自适应选择剪枝掩码” 的灵活策略。
总结:SparseGPT 的核心创新:通过 “逐列迭代 + 共享 Hessian 逆矩阵 + 分块自适应掩码”,在不重训练的前提下,高效压缩大模型(如 175B 参数):
-
用数学近似降低计算复杂度(从 \(O(d_{\text{hidden}}^4)\) 到 \(O(d_{\text{hidden}}^3)\) ),让超大规模模型剪枝可行;
-
支持非结构化(左侧)和半结构化(如 n:m 模式,右侧分块逻辑可扩展)稀疏,适配不同硬件加速需求。
简单说,这张图可视化了 “如何用低成本数学近似,给千亿参数模型‘瘦身’” 的核心流程 。
计算复杂度
总体成本包括三个部分:(a) 初始 Hessian 矩阵的计算,其时间复杂度为 Θ(n・dₒₗ²),其中 n 是所用输入样本的数量 —— 我们发现,即使在非常大的模型上,将样本数量 n 取为 dₒₗ的小倍数也足以获得良好且稳定的结果(见附录 A);(b) 迭代逆 Hessian 序列的时间复杂度为 O (dₒₗ³);以及 (c) 重构 / 剪枝本身。后者的成本上限可以是依次对 W 的所有 dᵣₒᵥ行和所有 dₒₗ列应用式 (3) 所需的时间,即 O (dₒₗ・dᵣₒᵥ・dₒₗ)。总体而言,总时间复杂度为 O (dₒₗ³ + dᵣₒᵥ・dₒₗ²)。对于 Transformer 模型,这简单来说就是 O (dₕᵢddₑₙ³),因此比精确重构效率高出 dₕᵢddₑₙ倍。这意味着我们已经实现了最初的目标,因为这种复杂度足以使我们的方案实用,即使对于超大型模型也是如此。
权重冻结解释
虽然我们将 SparseGPT 算法描述为使用最优部分更新对精确重构的近似,但对该方案还有另一种有趣的理解。具体而言,考虑一种精确的贪心框架,该框架逐列压缩权重矩阵,在每一步中总是最优地更新所有尚未压缩的权重(Frantar 等人,2022b;a)。乍一看,SparseGPT 似乎不符合这一框架,因为我们仅压缩每列中的部分权重,并且也只更新部分未压缩的权重。然而,从机制上讲,“压缩” 权重最终意味着将其固定为某个特定值,并确保它不会通过未来的更新被 “解压缩”,即它被冻结了。因此,通过将逐列压缩定义为: \(compress\left(w^{j}\right)_{i}=0 if j \notin M_{i} and w_{i}^{j} otherwise \quad(6)\), 即对不在掩码中的权重置零,并将其余权重固定为其当前值,我们的算法可以被解释为一种精确的逐列贪心方案。这种观点将使我们能够干净地将稀疏化和量化合并到单个压缩过程中。
3.2 自适应掩码选择
到目前为止,我们仅关注了权重重构,即假设剪枝掩码 M 是固定的。按照 AdaPrune(Hubara 等人,2021a)的思路,决定掩码的一种简单方法是通过幅度剪枝(Zhu & Gupta,2017)。然而,最近的工作(Frantar 等人,2022b)表明,剪枝过程中的更新会由于相关性而显著改变权重,并且在掩码选择中考虑这一点会产生更好的结果。这一见解可以通过在运行重构时自适应地选择掩码来整合到 SparseGPT 中。
实现这一点的一种明显方法是在压缩每列 i 时选择最容易剪枝的 p% 权重,从而实现 p% 的整体稀疏度。这种方法的主要缺点是稀疏度不能在列之间非均匀分布,从而施加了不必要的额外结构。这对于大型语言模型来说尤其成问题,因为它们存在少量高度敏感的异常特征(Dettmers 等人,2022;Xiao 等人,2022)。
我们通过迭代分块消除了这一缺点。更准确地说,我们总是一次为 Bₛ=128 列选择剪枝掩码(见附录 A),基于式 (3) 中的 OBS 重构误差 ε,使用我们 Hessian 序列中的对角线值。然后,我们执行接下来的 Bₛ次权重更新,之后再为下一个块选择掩码,依此类推。这个过程允许每列进行非均匀选择,特别是还可以使用相应的 Hessian 信息,同时也考虑先前的权重更新来进行选择。(对于单个列 j,选择标准变为幅度,因为 [H⁻¹]ⱼⱼ在所有行中都是恒定的。)
3.3 对半结构化稀疏度的扩展
SparseGPT 也很容易适应半结构化模式,例如流行的 n:m 稀疏格式(Zhou 等人,2021;Hubara 等人,2021a),该格式在 Ampere NVIDIA GPU 上的 2:4 实现中提供了加速。具体而言,每连续 m 个权重应恰好包含 n 个零。因此,我们可以简单地选择块大小 Bₛ=m,然后通过根据式 (3) 选择产生最低误差的 n 个权重,在每行的掩码选择中强制执行零约束。类似的策略也可应用于其他半结构化剪枝模式。最后,我们注意到在这种半结构化场景中,更大的 B 不会有用,因为零不能在不同的大小为 m 的列集之间非均匀分布。
3.4 完整算法伪代码
算法 1 SparseGPT 算法。给定逆 Hessian 矩阵 H⁻¹=(XX⊤+λI)⁻¹、惰性批更新块大小 B 和自适应掩码选择块大小 Bₛ,我们将层矩阵 W 剪枝到 p% 的非结构化稀疏度;每 Bₛ个连续列将有 p% 的稀疏度。 M ← 1_{dᵣₒᵥ×dₒₗ} // 二进制剪枝掩码 E ← 0_{dᵣₒᵥ×B} // 块量化误差 H⁻¹ ← Cholesky (H⁻¹)⊤ // Hessian 逆信息 for i = 0, B, 2B, ... do for j = i, ..., i + B − 1 do if j mod Bₛ = 0 then M:,j:(j+Bₛ) ← (1−p)% 权重 wₙ∈W:,j:(j+Bₛ) 中具有最大 w²ₙ/[H⁻¹]²ₙₙ的掩码 end if E:,j−i ← W:,j / [H⁻¹]ⱼⱼ // 剪枝误差 E:,j−i ← (1−M:,j)・E:,j−i // 冻结权重 W:,j:(i+B) ← W:,j:(i+B)−E:,j−i・H⁻¹ⱼ,j:(i+B) // 更新 end for W:,(i+B): ← W:,(i+B): − E・H⁻¹ᵢ:(i+B),(i+B): // 更新 end for W ← W・M // 将剪枝权重设为 0
通过第 3.1 节末尾讨论的权重冻结解释,SparseGPT 重构可以纳入最近量化算法 GPTQ(Frantar 等人,2022a)的逐列贪心框架中。这意味着我们还可以从 GPTQ 继承一些算法增强,具体来说:通过 Cholesky 分解预计算所有相关的逆 Hessian 序列信息以实现数值稳健性,以及应用惰性批处理权重矩阵更新以提高算法的计算内存比。我们的自适应掩码选择及其对半结构化剪枝的扩展也与所有这些额外技术兼容。
算法 1 以完全开发的形式呈现了 SparseGPT 算法的非结构化稀疏度版本,整合了来自 GPTQ 的所有相关技术。
3.5 联合稀疏化与量化
算法 1 在 GPTQ 的逐列贪心框架中运行,因此共享计算 H⁻¹ 的 Cholesky 分解和持续更新 W 的计算密集型步骤。这使得将两种算法合并为单个联合过程成为可能。具体而言,SparseGPT 冻结的所有权重都会被额外量化,从而在后续更新步骤中需要补偿以下广义误差: \(E_{:, j-i} \leftarrow\left(W_{:, j}-M_{:, j} \cdot quant\left(W_{:, j}\right)\right) /\left[H^{-1}\right]_{j j} \quad(7)\), 其中 quant (w) 将 w 中的每个权重四舍五入到量化网格上的最近值。至关重要的是,在这种方案中,稀疏化和剪枝在单个过程中联合执行,其成本基本上不超过 SparseGPT。此外,联合执行量化和剪枝意味着后续的剪枝决策会受到早期量化舍入的影响,反之亦然。这与先前的联合技术(Frantar 等人,2022b)形成对比,后者首先对层进行稀疏化,然后简单地对剩余权重进行量化。
4. 实验
设置
我们在 PyTorch(Paszke 等人,2019)中实现 SparseGPT,并使用 HuggingFace Transformers 库(Wolf 等人,2019)处理模型和数据集。所有剪枝实验都在单个配备 80GB 内存的 NVIDIA A100 GPU 上进行。在这种设置下,SparseGPT 可以在大约 4 小时内完全稀疏化 1750 亿参数的模型。与 Yao 等人(2022);Frantar 等人(2022a)类似,我们按顺序稀疏化 Transformer 层,这显著降低了内存需求。我们所有的实验都是一次性进行的,没有微调,与最近关于 GPT 规模模型训练后量化的工作设置相似(Frantar 等人,2022a;Yao 等人,2022;Dettmers 等人,2022)。此外,在附录 E 中,我们研究了使用现有工具对我们的稀疏模型进行实际加速的效果。
对于校准数据,我们遵循 Frantar 等人(2022a)的做法,使用从 C4 数据集(Raffel 等人,2020)的第一个分片随机选择的 128 个 2048 token 片段。这代表了从互联网爬取的通用文本数据,并确保我们的实验实际上保持零样本,因为剪枝过程中没有看到任何特定任务的数据。
模型、数据集和评估
我们主要使用 OPT 模型家族(Zhang 等人,2022)来研究缩放行为,但也考虑了 1760 亿参数版本的 BLOOM(Scao 等人,2022)。虽然我们的重点是最大的变体,但我们也展示了一些较小模型的结果,以提供更全面的情况。
在指标方面,我们主要关注困惑度,已知这是一种具有挑战性且稳定的指标,非常适合评估压缩方法的准确性(Yao 等人,2022;Frantar 等人,2022b;Dettmers & Zettlemoyer,2022)。我们考虑 raw-WikiText2(Merity 等人,2016)和 PTB(Marcus 等人,1994)的测试集以及 C4 验证数据的一个子集,这些都是 LLM 压缩文献中流行的基准(Yao 等人,2022;Park 等人,2022a;Frantar 等人,2022a;Xiao 等人,2022)。为了提高可解释性,我们还提供了 Lambada(Paperno 等人,2016)、ARC(Easy 和 Challenge)(Boratko 等人,2018)、PIQA(Tata & Patel,2003)和 StoryCloze(Mostafazadeh 等人,2017)的零样本精度结果
我们注意到,我们评估的主要重点是稀疏模型相对于密集基线的准确性,而不是绝对数值。不同的预处理可能会影响绝对准确性,但对我们的相对结论影响很小。困惑度的计算严格遵循 HuggingFace(HuggingFace,2022)描述的程序,使用全步长。我们的零样本评估是通过 GPTQ(Frantar 等人,2022a)的实现进行的,而 GPTQ 的实现又基于流行的 EleutherAI-evalharness(EleutherAI,2022)。更多评估细节可在附录 B 中找到。所有密集和稀疏结果都是使用完全相同的代码计算的,代码作为补充材料提供,以确保公平比较。
基线
我们与标准的幅度剪枝基线(Zhu & Gupta,2017)进行比较,该基线按层应用,可扩展到最大的模型。在高达 10 亿参数的模型上,我们还与 AdaPrune(Hubara 等人,2021a)进行比较,这是现有精确训练后剪枝方法中效率最高的。为此,我们使用 Frantar & Alistarh(2022)的内存优化重新实现,并进一步调整了 AdaPrune 作者提供的超参数。因此,对于我们感兴趣的模型,我们实现了约 3 倍的加速,且不影响解决方案质量。
4.1 结果
剪枝与模型大小的关系
我们首先研究剪枝 LLM 的难度如何随其大小变化。我们考虑整个 OPT 模型家族,并按标准做法(Sanh 等人,2020;Kurtic 等人,2022)均匀剪枝所有线性层(不包括嵌入层和头部)至 50% 的非结构化稀疏度、完整的 4:8 或完整的 2:4 半结构化稀疏度(2:4 模式最严格)。raw-WikiText2 的性能数据如表 1 所示,并在图 2 中可视化。PTB 和 C4 的相应结果可在附录 C 中找到,总体趋势非常相似。
一个直接的发现是,幅度剪枝模型的准确性在所有规模上都崩溃了,更大的变体通常下降得更快。这与较小的视觉模型形成鲜明对比,视觉模型通常可以通过简单的幅度选择剪枝到 50% 或更高的稀疏度,且精度损失很小(Singh & Alistarh,2020;Frantar 等人,2022b)。这凸显了精确剪枝器对于大规模生成式语言模型的重要性,同时也表明困惑度是一个非常敏感的指标。
对于 SparseGPT,趋势则大不相同:在 27 亿参数时,困惑度损失约为 1 点;在 660 亿参数时,基本上没有损失;而在最大规模时,相对于密集基线甚至有轻微的准确性提升,不过这似乎是数据集特定的(另见附录 C)。不出所料,AdaPrune 相对于幅度剪枝也有很大改进,但精度明显低于 SparseGPT。尽管 AdaPrune 效率很高,但在 35 亿参数模型上运行它大约需要 1.3 小时,在 13 亿参数模型上需要约 4.3 小时,而 SparseGPT 在同一 A100 GPU 上可以在大致相同的时间内完全稀疏化 660 亿和 1750 亿参数的模型。
总的来说,存在一个明显的趋势:更大的模型更容易被稀疏化,我们推测这是由于过参数化。对这一现象的详细研究将是未来工作的一个好方向。对于 4:8 和 2:4 稀疏度,行为类似,但由于稀疏模式更受约束(Hubara 等人,2021a),精度下降通常更大。尽管如此,在最大规模下,4:8 和 2:4 稀疏度的困惑度增加分别仅为 0.11 和 0.39。
1000 多亿参数模型的稀疏度缩放
接下来,我们仔细研究最大的公开可用密集模型 OPT-175B 和 BLOOM-176B,并研究它们的性能如何随 SparseGPT 或幅度剪枝引起的稀疏度程度而变化。结果在图 1 和图 5 中可视化。
对于 OPT-175B 模型(图 1),幅度剪枝在显著精度损失发生前最多只能达到 10% 的稀疏度;同时,SparseGPT 能够在困惑度增加相当的情况下实现高达 60% 的稀疏度。BLOOM-176B(图 5)似乎更适合幅度剪枝,最多可在无重大损失的情况下达到 30% 的稀疏度;
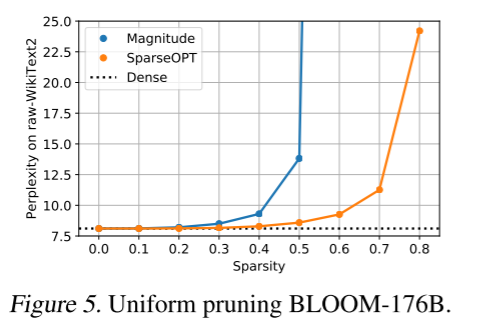
尽管如此,SparseGPT 仍能在类似的困惑度下降水平下实现 50% 的稀疏度,提升了 1.66 倍。即使在 80% 的稀疏度下,经 SparseGPT 压缩的模型仍然获得合理的困惑度,而幅度剪枝在 OPT 和 BLOOM 分别达到 40% 和 60% 的稀疏度时就导致完全崩溃(困惑度 > 100)。值得注意的是,SparseGPT 从这些模型中移除了约 1000 亿个权重,对精度的影响很小。
零样本实验
为了补充困惑度评估,我们提供了几个零样本任务的结果。已知这些评估相对嘈杂(Dettmers 等人,2022),但更具可解释性。请参见表 2。
总体而言,类似的趋势仍然存在,幅度剪枝模型的性能下降到接近随机水平,而 SparseGPT 模型保持接近原始精度。然而,正如预期的那样,这些数值更嘈杂:尽管 2:4 剪枝是约束最严格的稀疏模式,但在 Lambada 上的精度明显高于密集模型。当考虑许多不同任务时,这些影响最终会平均化,这与文献一致(Yao 等人,2022;Dettmers 等人,2022;Dettmers & Zettlemoyer,2022)。
联合稀疏化与量化
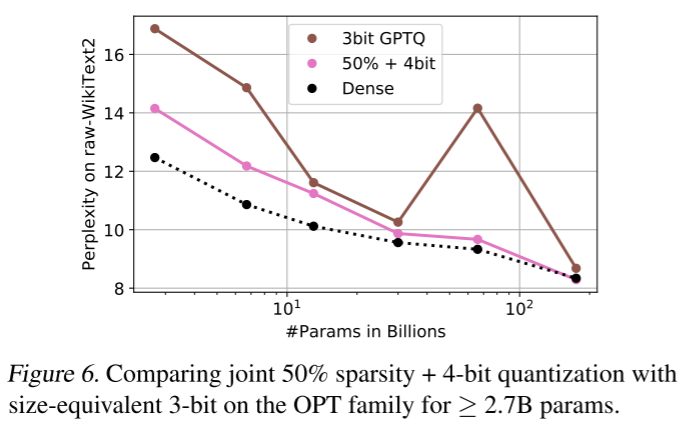
另一个有趣的研究方向是稀疏度和量化的结合,这将允许结合稀疏度带来的计算加速(Kurtz 等人,2020;Elsen 等人,2020)和量化带来的内存节省(Frantar 等人,2022a;Dettmers 等人,2022;Dettmers & Zettlemoyer,2022)。具体而言,如果我们将模型压缩至 50% 稀疏度 + 4 位权重,仅存储非零权重并使用位掩码指示其位置,那么其总体内存消耗与 3 位量化相同。
因此,在图 6(右)中,我们将 SparseGPT 50%+4 位与最先进的 GPTQ(Frantar 等人,2022a)3 位结果进行了比较。可以看出,对于 27 亿参数以上的模型(包括 1750 亿参数模型,其困惑度为 8.29,而 3 位量化为 8.68),50%+4 位模型比相应的 3 位模型更准确。我们还在 OPT-175B 上测试了 2:4 和 4:8 与 4 位量化的组合,得到的困惑度分别为 8.55 和 8.85,这表明 4 位权重量化仅在半结构化稀疏度基础上带来约 0.1 的困惑度增加。
敏感性与部分 N:M 稀疏度
关于 n:m 剪枝的一个重要实际问题是,当完全稀疏化的模型精度不够时该怎么办?整体稀疏度水平不能简单地均匀降低,而是必须选择一部分层进行完全的 n:m 稀疏化。我们现在研究在超大型语言模型的背景下,什么是好的选择:我们假设 OPT-175B/BLOOM-176B 的 2/3 层应剪枝到 2:4 稀疏度,并考虑跳过某一类型的所有层(注意力层、全连接 1 层、全连接 2 层)或跳过连续层的 1/3(前部、中部、后部)。结果如图 7 所示。
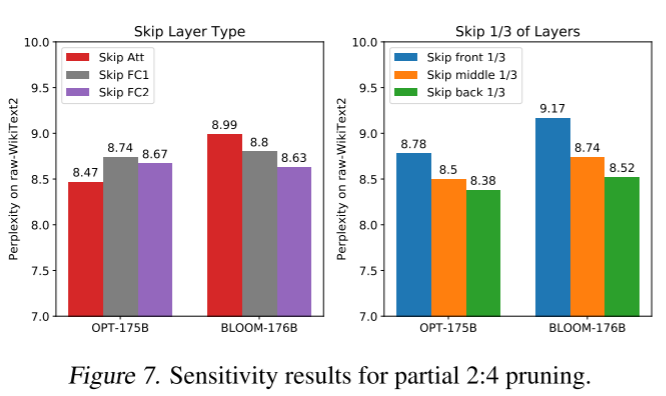
虽然不同模型对层类型的敏感性明显不同,但在模型部分方面似乎存在明显趋势:后面的层比前面的层更敏感;跳过模型的最后 1/3 层可获得最佳精度。这具有非常实际的意义,由于 SparseGPT 的顺序特性,我们可以通过将 SparseGPT 运行的前 x 层与原始模型的后 nₗₐᵧₑᵣₛ-x 层相结合,在单次剪枝过程中生成一系列 2:4 稀疏度逐渐增加的模型(例如 1/2、2/3、3/4 等)。此类模型序列的精度如附录 D 所示。
5. 相关工作
剪枝方法
据我们所知,我们是第一个研究大规模 GPT 规模模型(例如超过 100 亿参数)剪枝的团队。这一惊人差距的一个理由是,大多数现有剪枝方法(例如 Han 等人,2016;Gale 等人,2019;Kurtic & Alistarh,2022)需要在剪枝步骤后进行大量重训练才能恢复精度,而 GPT 规模模型通常需要大量计算和参数调整来进行训练或微调(Zhang 等人,2022)。
SparseGPT 是一种针对 GPT 规模模型的训练后方法,因为它不执行任何微调。到目前为止,训练后剪枝方法仅在经典 CNN 或 BERT 类型模型(Hubara 等人,2021a;Frantar 等人,2022b;Kwon 等人,2022)的规模上进行了研究,这些模型的权重比我们感兴趣的模型少 100-1000 倍。我们在第 2 节中讨论了扩展这些方法的挑战及其与 SparseGPT 的关系。
训练后量化
相比之下,关于开源 GPT 规模模型的训练后量化方法已有大量研究(Zhang 等人,2022;Scao 等人,2022)。具体而言,ZeroQuant(Yao 等人,2022)、LLM.int8 ()(Dettmers 等人,2022)和 nuQmm(Park 等人,2022a)方法研究了舍入到最近值量化用于十亿参数模型的可行性,表明通过这种方法对权重进行 8 位量化是可行的,但由于异常特征的存在,激活量化可能很困难。
Frantar 等人(2022a)利用近似二阶信息对最大模型的权重进行精确量化至 2-4 位,并表明当与高效 GPU 内核结合使用时,生成式批大小为 1 的推理速度可提高 2-5 倍。后续工作(Xiao 等人,2022)研究了激活和权重的联合 8 位量化,提出了一种基于平滑的方案,该方案降低了激活量化的难度,并辅以高效的 GPU 内核。
Park 等人(2022b)通过 quadapters 解决了量化激活异常值的困难,quadapters 是可学习的参数,其目标是按通道缩放激活,同时保持其他模型参数不变。Dettmers & Zettlemoyer(2022)研究了模型大小、量化位数和大规模 LLM 的不同精度概念之间的缩放关系,观察到困惑度分数与跨任务的聚合零样本精度之间存在高度相关性。
正如我们在第 3.5 节中所示,SparseGPT 算法可以与当前最先进的权重量化算法 GPTQ 结合应用,并且应该与激活量化方法兼容(Xiao 等人,2022;Park 等人,2022b)。
6. 讨论
我们提供了一种名为 SparseGPT 的新型训练后剪枝方法,专门为 GPT 家族的大规模语言模型量身定制。我们的结果首次表明,大规模生成式预训练 Transformer 家族模型可以通过权重剪枝一次性压缩至高度稀疏,无需任何重训练,且在困惑度和零样本性能方面的精度损失都很低。具体而言,我们已经表明,最大的开源 GPT 家族模型(例如 OPT-175B 和 BLOOM-176B)可以达到 50-60% 的稀疏度,移除超过 1000 亿个权重,且精度波动很小。
在局限性方面,我们主要关注均匀的每层稀疏度,但非均匀分布是未来工作的一个有前景的课题。此外,SparseGPT 目前在中小型变体上的精度不如在最大型变体上的精度。我们认为这可以通过仔细的部分或完全微调来解决,这在高达数十亿参数的模型规模上开始变得可行。最后,虽然我们在这项工作中研究了预训练基础模型的稀疏化,但我们认为研究额外的训练后技术(如指令微调或基于人类反馈的强化学习)如何与可压缩性相互作用也将是未来重要的研究领域。
总体而言,我们的工作表明,大规模 GPT 模型的高度参数化允许剪枝直接在密集模型的 “近邻” 中识别出稀疏的精确模型,而无需梯度信息。值得注意的是,此类稀疏模型的输出与密集模型的输出高度相关。我们还表明,更大的模型更容易被稀疏化:在固定的稀疏度水平下,随着模型大小的增加,更大的稀疏模型的相对精度下降会缩小,以至于在最大的模型上实现 50% 的稀疏度实际上不会导致精度下降,这对于未来压缩此类大规模模型的工作来说是非常令人鼓舞的。
附录 A 消融研究
在本节中,我们针对 SparseGPT 的几个主要参数进行消融研究。为了快速迭代并能够探索更多计算和内存密集型设置,我们在此重点关注 OPT-2.7B 模型。除非另有说明,我们始终将其均匀剪枝至默认的 50% 稀疏度。为简洁起见,我们仅在此显示 raw-WikiText2 的结果,但需要注意的是,在其他数据集上的行为非常相似。
校准数据量
首先,我们研究 SparseGPT 的精度如何随校准数据样本数量变化,我们以 2 的幂次变化样本数量。结果如图 8 所示。奇怪的是,即使仅使用几个 2048 token 片段,SparseGPT 已经能够取得不错的结果;然而,使用更多样本会带来显著的进一步改进,但仅在一定程度上,因为曲线很快就趋于平缓。因此,由于使用更多样本也会增加计算和内存成本,我们在所有实验中坚持使用 128 个样本。
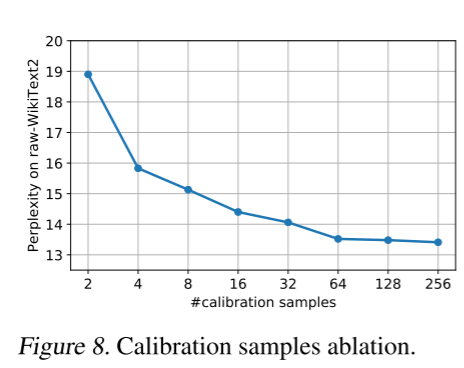
图 8. 校准样本消融实验。
Hessian 阻尼
接下来,我们通过测试以 10 的幂次变化的值(见图 9)来研究 Hessian 阻尼的影响,这些值按照(Frantar 等人,2022a)的方法乘以平均对角线值。总体而言,该参数似乎不太敏感,0.001 到 0.1 的表现相当相似;只有当阻尼非常高时,解决方案质量才会显著下降。我们选择 1%(即 0.01)的阻尼,以确保即使对于最大的模型,逆计算也是安全的。
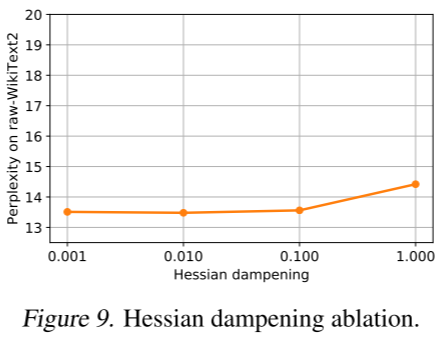
图 9. Hessian 阻尼消融实验。
掩码选择块大小
我们方法的另一个重要组成部分是自适应掩码选择,如图 10 所示,其中我们以 2 的幂次变化相应的块大小参数。列级(块大小 1)和接近完整块大小(4096 和 8192)的表现都明显差于合理的分块。有趣的是,广泛的块大小范围似乎都能很好地工作,几百左右的块大小精度略高。因此,我们选择 128 的块大小,它位于该范围内,同时由于与默认的惰性权重更新批大小匹配,稍微简化了算法实现。
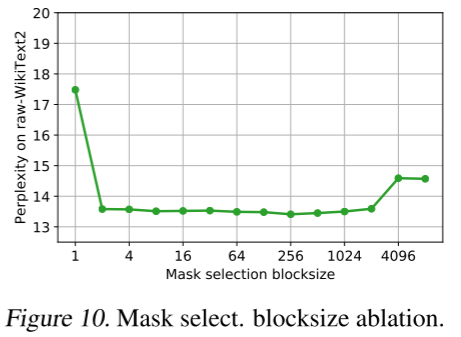
图 10. 掩码选择块大小消融实验。
对随机种子的敏感性
最后,我们确定我们算法的结果对随机性的敏感程度;具体而言,相对于校准数据的随机采样。我们使用不同的数据采样随机种子重复标准的 50% 剪枝运行 5 次,得到 13.52±0.075(均值 / 标准差),这表明 SparseGPT 对所使用的确切校准数据相当稳健,这与其他训练后工作中的观察结果一致(Nagel 等人,2020;Hubara 等人,2021b;Frantar 等人,2022b)。
A.1 近似质量
在本节中,我们研究 SparseGPT 采用的部分更新近似相对于(昂贵得多的)精确重构的损失有多大。我们再次考虑 50% 稀疏度下的 OPT-2.7B 模型,并在图 11 中绘制模型前半部分 SparseGPT 的逐层平方误差相对于精确重构误差(使用相同的掩码和 Hessian)的比例。除了早期注意力输出投影层中的一些异常值外,SparseGPT 的最终重构误差平均仅比精确重构差约 20%;在后面的全连接 2 层上,近似误差甚至接近仅 10%,可能是因为这些层的总输入数量非常多,因此考虑子集内相关性的损失比在较小的层上更轻微。总体而言,这些结果表明,尽管 SparseGPT 的速度显著提升,但仍保持了相当高的精度。
附录 B 评估细节
困惑度
如正文中所述,我们的困惑度计算以标准方式进行,严格遵循(HuggingFace,2022)的描述。具体而言,这意味着我们将测试 / 验证数据集中的所有样本连接起来,
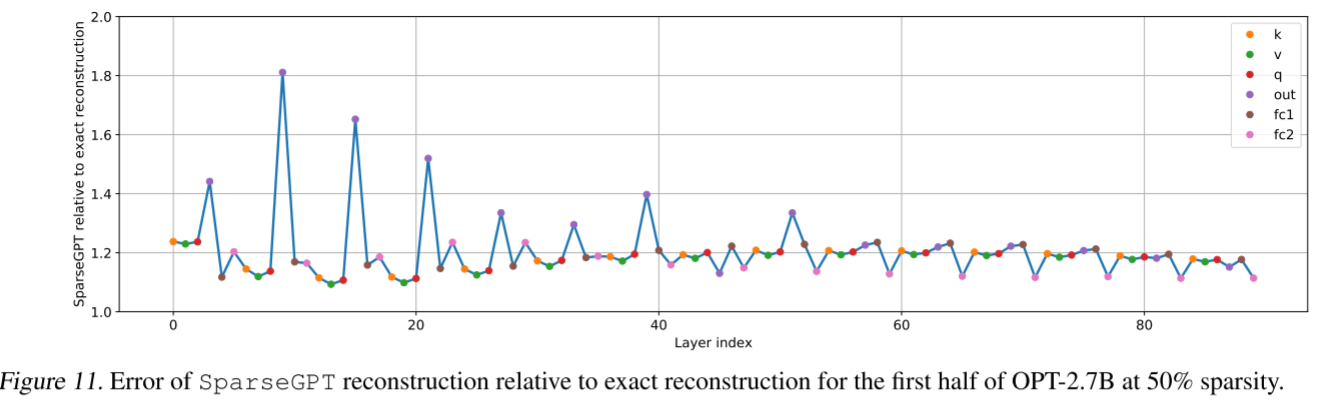
图 11. 在 50% 稀疏度下,OPT-2.7B 前半部分的 SparseGPT 重构误差相对于精确重构误差的比例。
用模型匹配的分词器对结果进行编码,然后将其分割为 2048 token 的非重叠片段(我们研究的模型的最大历史长度)。将这些片段输入模型以计算相应的平均语言建模损失。我们报告的困惑度是该数值的指数。
数据集
在数据集方面,我们使用 WikiText2 测试集的原始版本,并按照上述 HuggingFace 描述的建议,用 “\n\n” 连接样本,以生成格式正确的 markdown。对于 PTB,我们使用 HuggingFace 的 “ptb text only” 版本的测试集,并直接连接样本,不使用分隔符,因为 PTB 不应该包含任何标点符号。我们的 C4 子集由直接连接的验证集第一个分片的前 256 个 2048 编码 token 组成;做出这一选择是为了控制评估成本。
附录 C 额外结果
PTB 和 C4 上的剪枝难度缩放
表 3 和表 4 呈现了与正文中表 1 等效的结果,但分别基于 PTB 和我们的 C4 子集。总体而言,它们遵循与第 4.1 节中讨论的非常相似的趋势。主要值得注意的差异是,在最大模型上,50% 稀疏度下没有观察到相对于密集基线的轻微困惑度下降,因此我们将其标记为数据集特定现象。
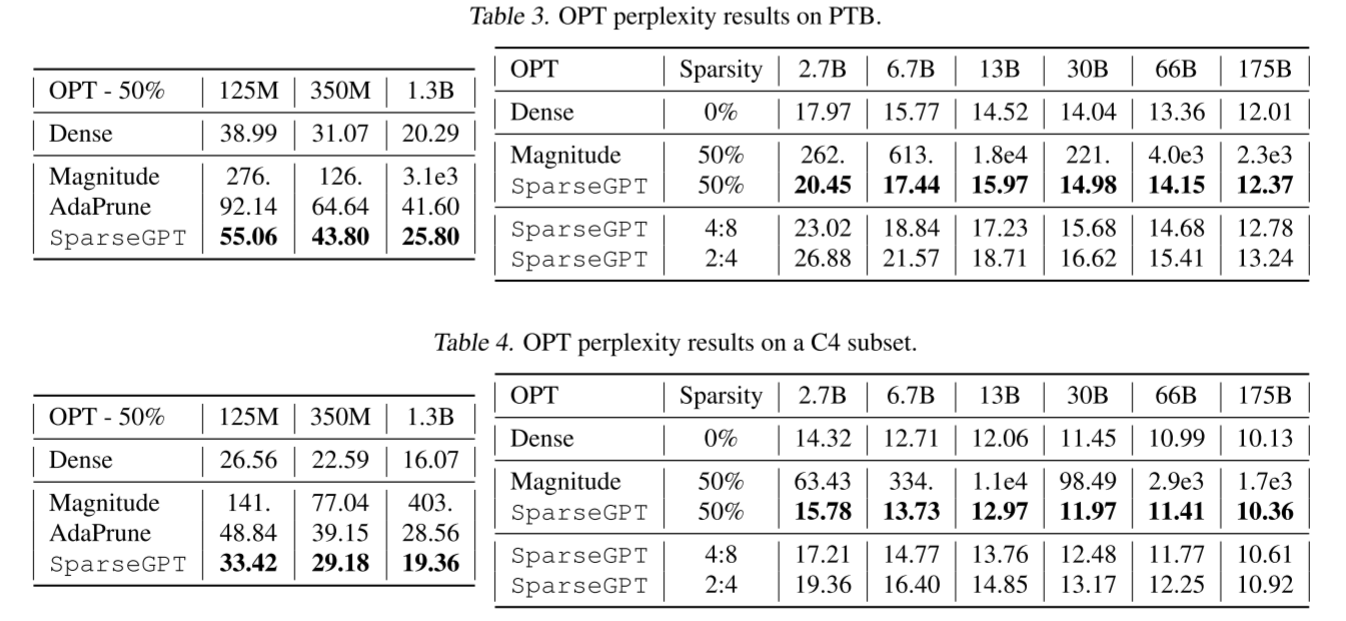
表 3. OPT 在 PTB 上的困惑度结果。
表 4. OPT 在 C4 子集上的困惑度结果。
50% 稀疏 + 3 位量化
正文中仅展示了 50%+4 位联合稀疏化和量化的近乎无损结果,其存储量相当于 3 位量化。对于 50%+3 位(相当于 2.5 位),OPT-175B 在 raw-WikiText2 上实现了 8.60 的 PPL,这也比 GPTQ(Frantar 等人,2022a)的最先进 2.5 位结果 8.94 更准确。SparseGPT 在 4:8+3 位上的得分相同,为 8.93。基于这些初步研究,我们认为结合稀疏度 + 量化是朝着更大规模语言模型更极端压缩方向发展的一个有前景的方向。
附录 D 部分 2:4 结果
表 5 和表 6 显示了一系列部分 2:4 稀疏模型在三个不同语言建模数据集上的性能。前一部分层被完全稀疏化,而其余层保持密集。通过这种方式,也可以通过二进制压缩选择(如 n:m 剪枝)来权衡加速和精度。
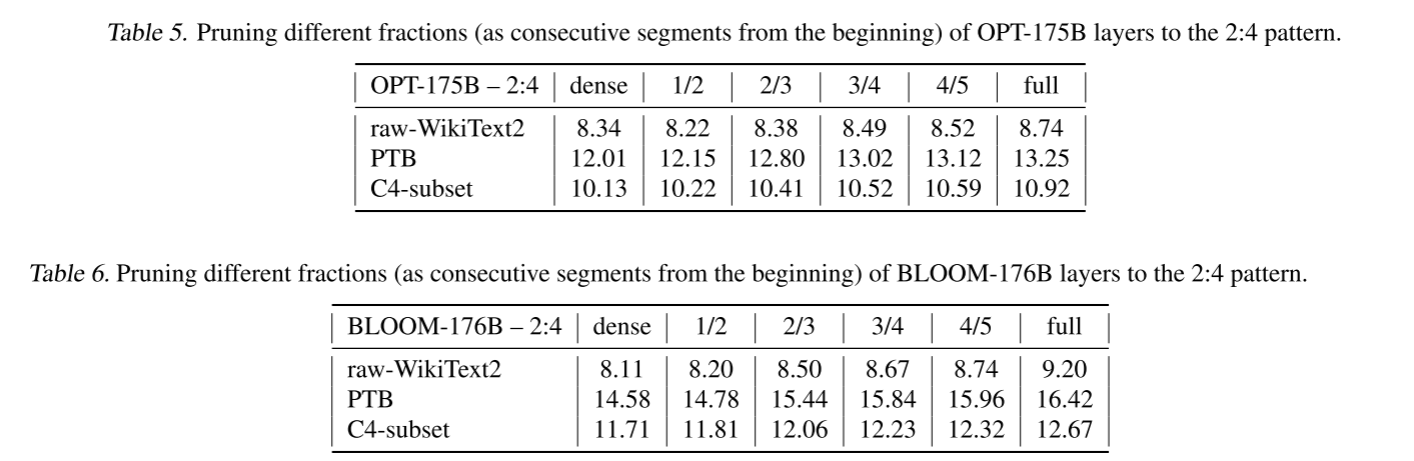
表 5. 将 OPT-175B 的不同比例(从开始的连续片段)层剪枝到 2:4 模式的结果。
表 6. 将 BLOOM-176B 的不同比例(从开始的连续片段)层剪枝到 2:4 模式的结果。
附录 E 稀疏度加速
最后,我们对现有的现成工具在实践中对稀疏语言模型的加速效果进行了初步研究,包括 CPU 和 GPU 推理。我们认为,通过更多的模型特定优化,这些结果可能会显著改善,这是未来工作的一个重要课题。
CPU 加速
首先,我们研究非结构化稀疏度对 CPU 推理的加速效果。为此,我们利用最先进的 DeepSparse 引擎(NeuralMagic,2022),在 Intel (R) Core (TM) i9-7980XE CPU @ 2.60GHz(使用 18 核)上对 OPT-2.7B(更大变体的支持似乎仍在开发中)进行端到端推理,批大小为 400 token。表 7 显示了运行稀疏模型相对于在相同引擎 / 环境中运行的密集模型的端到端加速比。(作为参考,密集 DeepSparse 比标准 ONNXRuntime 快 1.5 倍。)所实现的加速比接近理论最优,这表明用于 LLM 推理的 CPU 非结构化稀疏度加速已经相当实用。

表 7. 在 DeepSparse 中运行稀疏化的 OPT-2.7 模型相对于密集版本的加速比。
GPU 加速
NVIDIA Ampere 及更新代 GPU 支持的 2:4 稀疏度理论上可提供 2 倍的矩阵乘法加速。我们现在评估对于我们感兴趣的特定模型中出现的矩阵乘法问题规模,实际加速比有多大。我们使用 NVIDIA 的官方 CUTLASS 库(选择相应 profiler 返回的最优内核配置),并与高度优化的密集 cuBLAS 数值(PyTorch 也使用)进行比较。我们假设批大小为 2048 token,并基准测试 OPT-175B 中出现的三种矩阵形状;结果如表 8 所示。我们通过 2:4 稀疏度测量到各个层的加速比非常可观,在 54-79% 之间(端到端加速比可能会略低,因为存在一些额外开销,例如注意力计算)。
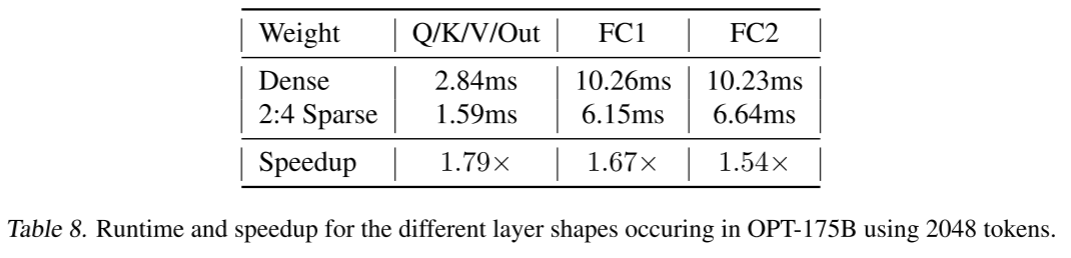
表 8. 使用 2048 token 时,OPT-175B 中不同层形状的运行时间和加速比。
附录 F 列稀疏度
在 3.1 节中,我们在行 - Hessian 挑战的背景下讨论了剪枝整列比剪枝单个权重明显更具挑战性,我们现在通过简要的消融研究来证明这一点。
具体而言,我们剪枝所有线性层中的整列(FC1 除外,因为在 FC2 中删除一列会自动删除 FC1 中的一行)。对于列掩码选择,我们使用 SparseGPT 的修改版本,该版本跨行求和(也受益于中间更新),然后使用所有剩余列进行完整重构,这在这种结构化设置中是可行的。表 9 总结了我们在几个 OPT 模型上的 raw-WikiText2 结果。
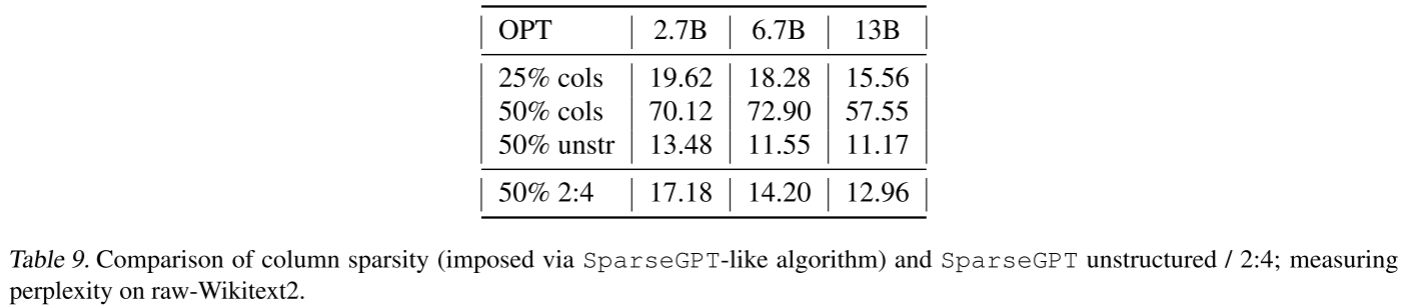
表 9. 列稀疏度(通过类 SparseGPT 算法实现)与 SparseGPT 非结构化 / 2:4 稀疏度的比较;在 raw-Wikitext2 上测量困惑度。
可以看出,50%(列)模型远非可用,即使仅 25% 的列剪枝仍然明显不如完整的 2:4 剪枝。尽管如此,我们认为对此类模型的一次性结构化剪枝值得进一步研究,例如,少量结合非结构化 / 半结构化稀疏度。
