埃氏筛|树dfs|差分计数
lc525
把数组里的0换成-1,求子数组和为零的最长长度
用哈希表记录前缀和首次出现的位置
通过找相同前缀和的位置差
得出最长的0和1数量相等的子数组长度。
class Solution {
public:
int findMaxLength(vector<int>& nums) {
unordered_map<int,int>hashtable;
int sum=0,ans=0;
hashtable[0]=-1;
for(int i=0; i<nums.size(); i++){
if(nums[i]==0)
nums[i]=-1;
sum+=nums[i];
if(hashtable.find(sum)!=hashtable.end())
ans=max(ans,i-hashtable[sum]);
else
hashtable[sum]=i;
}
return ans;
}
};
lc2779
差分计数
class Solution {
public:
int maximumBeauty(vector<int>& nums, int k) {
int minVal = *min_element(nums.begin(), nums.end());
int maxVal = *max_element(nums.begin(), nums.end());
int offset = minVal - k;
int len = (maxVal + k)+ 2;
vector<int> diff(len, 0);
for (int n : nums) {
int l = max(0, n - k);
int r = n + k + 1; // +1是差分数组的区间结束处理
diff[l]++;
diff[r]--;
}
int ret = 0, cnt = 0;
for (int d : diff) {
cnt += d;
ret = max(ret, cnt);
}
return ret;
}
};
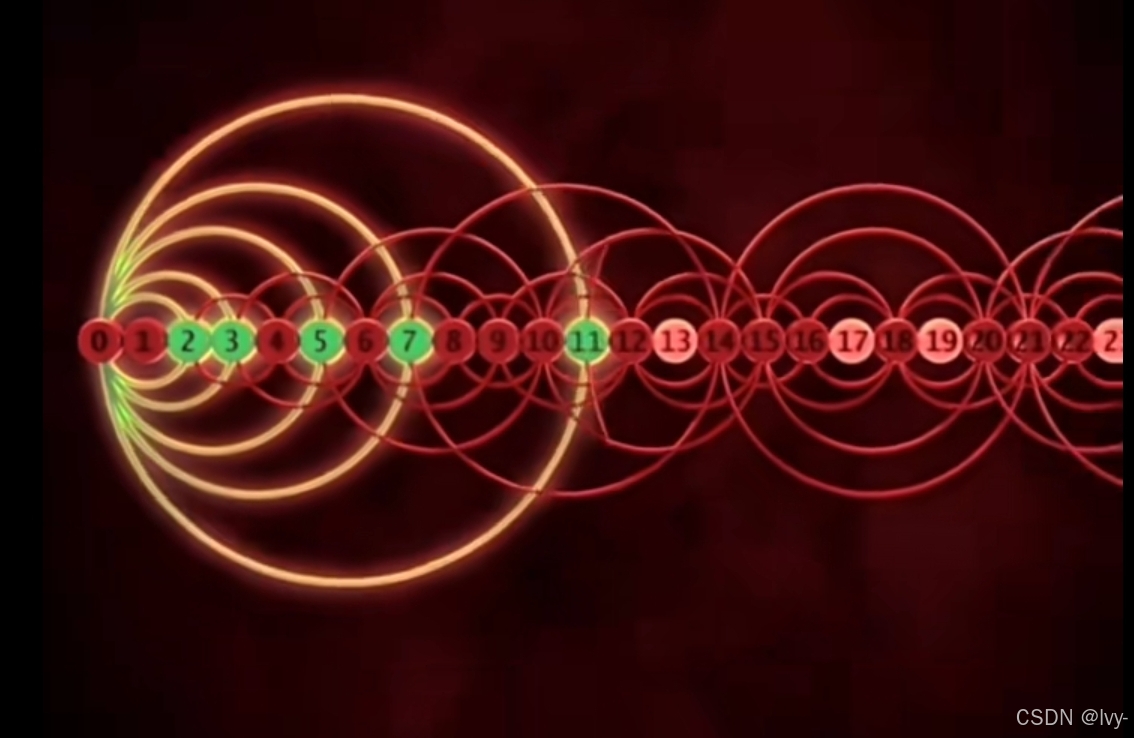
埃氏筛
探索宇宙universe
void init = []() {
np[1] = true;
for (int i = 2; i * i <= MX; i++) {
if (!np[i]) {
for (int j = i * i; j <= MX; j += i) {
np[j] = true;
}
}
}();
lc2867
埃氏筛 + 图的遍历
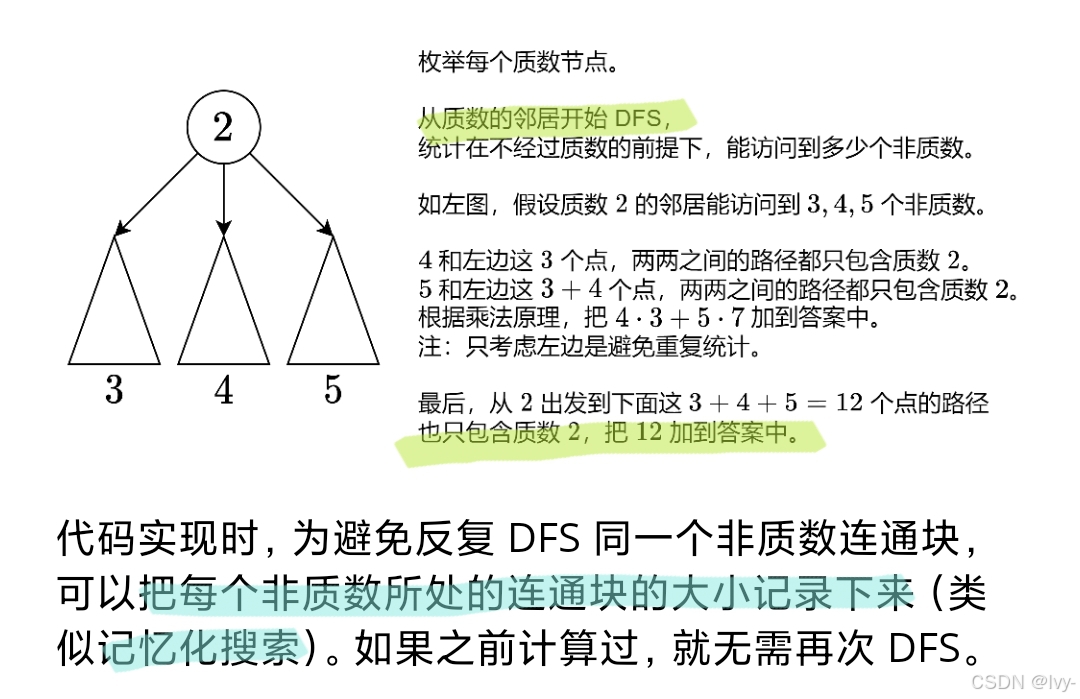
实现统计满足特定条件(路径关联质数节点)的路径数量:
1. 埃氏筛初始化:用匿名函数(C++ lambda 结合立即调用 init ),标记 1~1e5 内非质数,为后续判断节点是否为质数做准备。
2. 图处理逻辑:构建图结构,通过 dfs 遍历图,统计以质数节点为“枢纽”的连通块信息(非质数节点数量),结合数学计算,统计满足路径要求(路径关键节点为质数)的总路径数
const int MX = 1e5;
bool np[MX + 1]; // 质数=false 非质数=true
int init = []() {
np[1] = true;
for (int i = 2; i * i <= MX; i++) {
if (!np[i]) {
for (int j = i * i; j <= MX; j += i) {
np[j] = true;
}
}
}
return 0;
}();
class Solution {
public:
long long countPaths(int n, vector<vector<int>> &edges) {
vector<vector<int>> g(n + 1);
for (auto &e: edges) {
int x = e[0], y = e[1];
g[x].push_back(y);
g[y].push_back(x);
}
vector<int> size(n + 1);
vector<int> nodes;
function<void(int, int)> dfs = [&](int x, int fa) {
nodes.push_back(x);
for (int y: g[x]) {
if (y != fa && np[y]) {
dfs(y, x);
}
}
};
long long ans = 0;
for (int x = 1; x <= n; x++)
{
if (np[x]) continue; // 跳过非质数
int sum = 0;
for (int y: g[x]) { // 质数 x 把这棵树分成了若干个连通块
if (!np[y]) continue;
if (size[y] == 0) { // 尚未计算过
nodes.clear();
dfs(y, -1); // 遍历 y 所在连通块,在不经过质数的前提下,统计有多少个非质数
for (int z: nodes) {
size[z] = nodes.size();
}
}
// 这 size[y] 个非质数与之前遍历到的 sum 个非质数,两两之间的路径只包含质数 x
ans += (long long) size[y] * sum;
sum += size[y];
}
ans += sum; // 从 x 出发的路径
}
return ans;
}
};
lambda函数调用
埃氏筛部分 函数的调用方式
C++ lambda 函数, () 是立即调用语法,属于匿名函数的即时执行场景
