NFC 电路理论计算
本节主要介绍NFC设计中功率的最大传输理论,以及器件选型计算依据
最大功率传输
1.源/发生器的功率匹配条件让我们对于我们将要叙述的主题给出一个简要的叙述。
当我们想使由正弦波发生器产生的内部阻抗Z。与负载Z匹配时,需要满足一些特定的条件。记住这
个,利用发生器的戴维南等效电路,我们计算得到能够将最大有效功率传入负载所需的插入负载的值。消耗在负载上的平均功率:
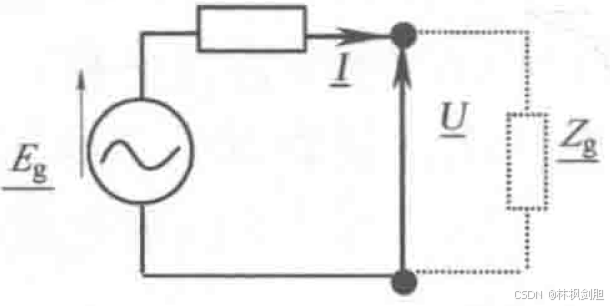
消耗在负载上的平均功率:![]()
通过设置Z=R+jX和Zg=Rg+jXg.:
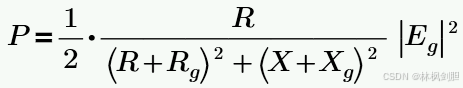
导数在R=R,时,值为0,这意味着发生器的内阻抗为Z,,电动势的均方误差为E,在负载阻抗与内部阻抗的复共轭相等时,例如Z=Z,负载将会得到最大的功率。最大功率为![]()
当内部阻抗与负载均为纯电阻时,计算接收端的功率效率可推导为:
![]()
在功率匹配的情况下,能量效率为50%。能量源提供了所有的能量,一半的能量被负载消耗了;剩下的一半由于焦耳效应消耗在发生器的内部电阻上。
例如,假如源的集成电路R_ic_out=R_gene=xΩ,负载必须达到xohm才能达到最好的匹配。
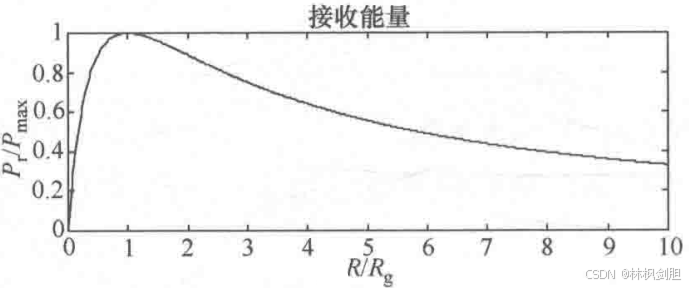
因此,知晓集成电路的R_ic_out是非常重要的,这样才能从本质上知晓有多少能量被传输到了负载上。例如,NXP给出的集成电路NFCPN532的操作说明书中呈现了了在不同的发生器模式下的曲线P=f(R)(如图所示)。这个曲线是对称的,指出了两件结论:
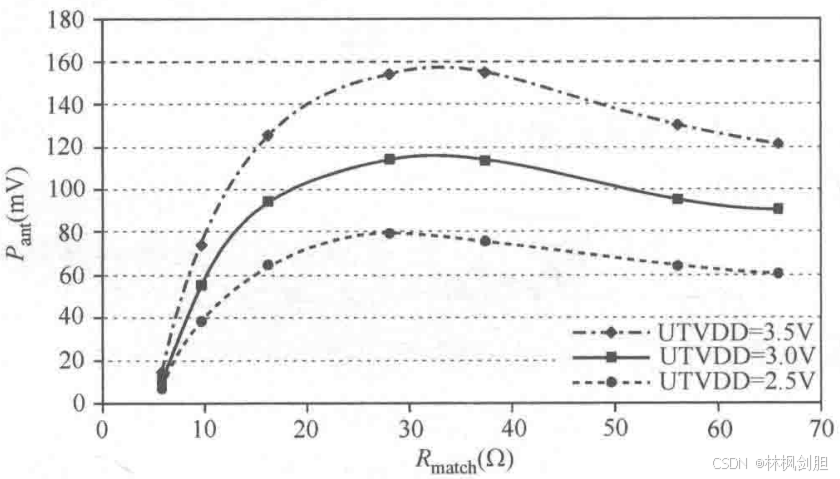
1) 在产生最大磁场强度H_max时,最优的R_match_differential 数值为35~40Ω;
2) 如同我们从曲线中看出来的,最大功率区域是相当扁平的的,当我们接近"匹配"阻抗时我们并没有损失太多的能量。因此,当使用相同功率的供给电压时,内部阻抗R_ic_out与负载阻抗越匹配,电流越小,需要从给端得到的能量越小。因此,假如我们想要最优化集成电路从直流电源获得能量,获得需要的H_max值时,R_match_differential应该接近60~70Ω。因此,当制造商不能够知道终端用户到底是什么样的需求,他们一般要求匹配电阻R_match_differential≈50Ω。
集成电路的配置
一般使用差分模式进行驱动,这里只介绍差分模式;
"差分模式"的输出在对称输出的初始设置中(不同的模式,如图所示,也就是Antl和Ant2之间),两个内部的输出Ant2按照所谓的"H桥"进行操作。
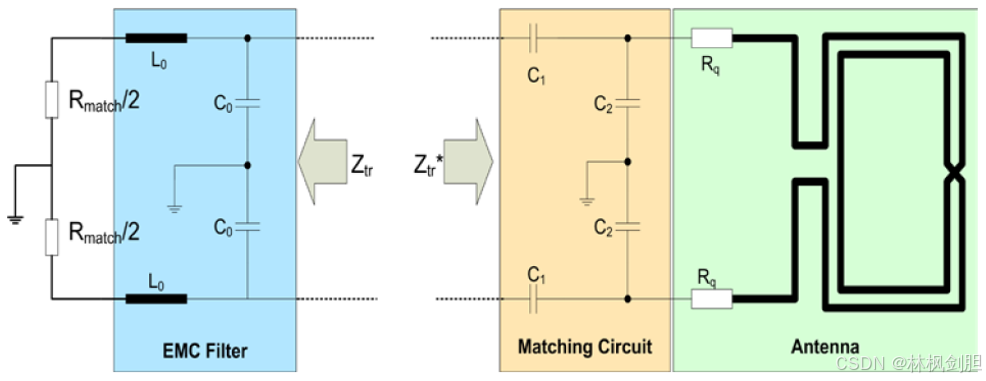
这让我们对于初始设置中的峰-峰值电压加倍(例如获得等于电路供电电压的两倍的应用于整个网络的电压V_out_pp),内部阻抗为两倍于差分模式下的阻抗2R_int_single-ended,而不是单端口模式下的R_int_single-eended匹配负载等于2R_int_single-ended时在差分模式下的可用功率的均方误差,因此:P_differential是P_single-ended上的两倍。
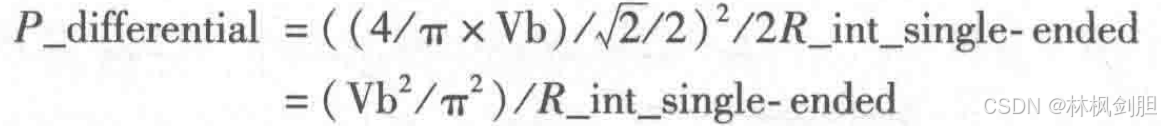
自然,发生器上也消耗了相同的能量。
提示:除非滤波器(和匹配部分)的费用加倍,初始设置体现见了两个优点。
1)可用功率加倍,如上所述,因此对于工作距离提供了增加的空间;
2)将集合当做一个参考的潜力,初始设置呈现了在天线线圈末端的电场E的对称辐射模式,没有改变由线圈产生的,应用又需求的磁场强度H,又避免了EMC干扰的直接影响,如图所示。
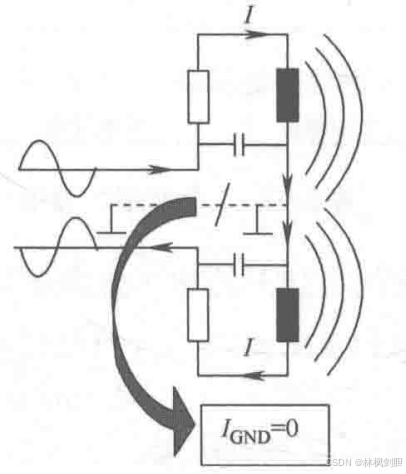
总结:差动初始设置
差动震荡器的内部阻抗:
