94. 城市间货物运输 I, Bellman_ford 算法
94. 城市间货物运输 I
Bellman_ford 算法
Bellman_ford 算法 与 dijkstra算法 相比通用性更强。
dijkstra算法解决不了负权边的问题,因为Dijkstra基于贪心策略,一旦一个节点被从队列中取出(标记为已解决),它就假定已经找到了到达该节点的最短路径。如果存在负权边,可能会有一条通过负权边的路径去到达该节点,这个负权边可以让一个已经被标记为已解决的节点的距离变得更小,但算法不会再回头去检查它,从而导致错误的结果。
Bellman_ford 算法的核心思想是 对所有边进行松弛n-1次操作(n为节点数量),从而求得目标最短路。
什么是松弛?
松弛是Bellman_ford 算法的实现基础。
松弛就是一个“检查并更新”的过程:检查是否存在一条通过某个中间节点的更短路径,如果存在,就更新当前的最短路径估计。其实就是更新min_List数组,来判断从起点出发到达下一个点是否有更短的路径。
代码实现:
# 对边 (u, v) 进行松弛操作
if dist[u] + weight(u, v) < dist[v]:dist[v] = dist[u] + weight(u, v)prev[v] = u # 可选:记录v是从u来的为什么是n-1次?
因为任何不包含负权环的最短路径最多包含 n-1 条边。n-1 次松弛足以保证找到所有可能的最短路径。 即n个点的话,从起点出发到终点的最短路径只需要经过n-1条边。
Bellman_ford 算法为什么能解决负权边的问题?
为什么dijkstra算法不能解决负权边的问题,关键是visited数组的设置导致了即使有负权边通向某个结节点,但由于visited中该节点之前被访问过了,因此无法更新。
Bellman-Ford 算法不依靠visited数组,其实现就是从每个点出发去松弛n-1次,来得到从起点出发经过该节点到达下一个节点时的最短路径。如下
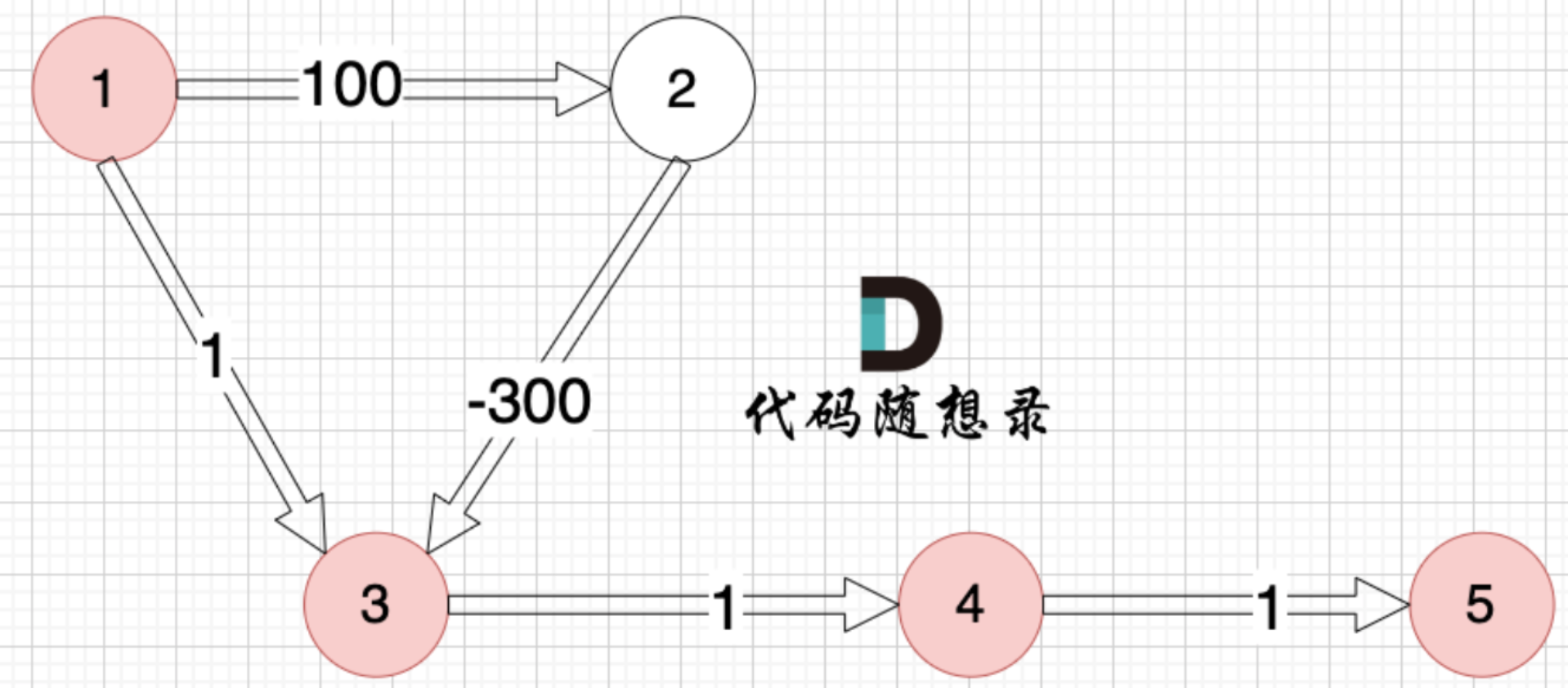
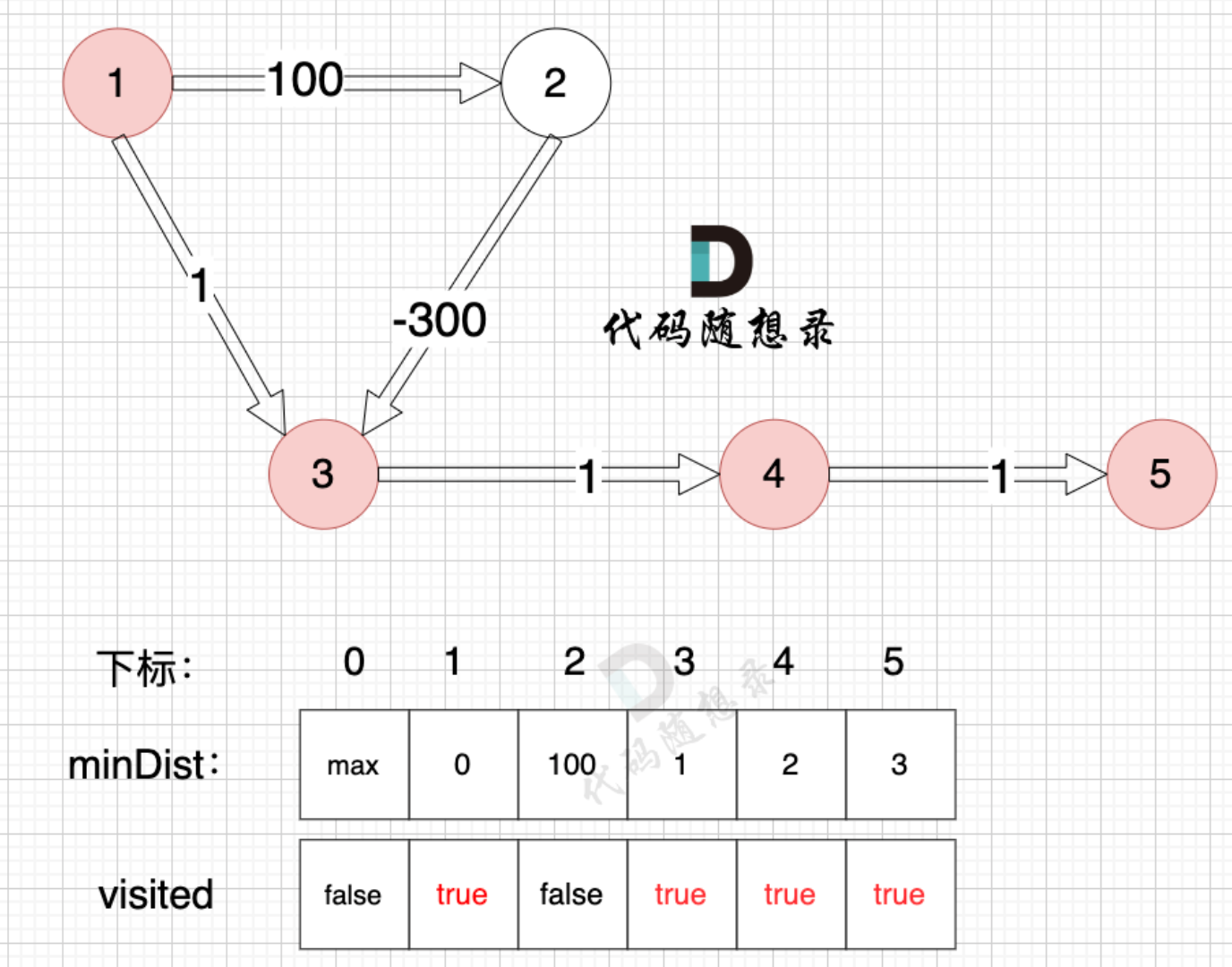
dist 初始化为 [ ∞, 0, ∞, ∞, ∞, ∞ ],n=5,因此需要松弛4次。
第一次松弛:
- 边
1→2(100): dist[1] + 100 = 0 + 100 = 100 < ∞ → 更新 dist[2] = 100 - 边
1→3(1): dist[1] + 1 = 0 + 1 = 1 < ∞ → 更新 dist[3] = 1 - 边
2→3(-300): dist[2] + (-300) = 100 - 300 = -200 < 1 → 更新 dist[3] = -200 - 边
3→4(1): dist[3] + 1 = -200 + 1 = -199 < ∞ → 更新 dist[4] = -199 - 边
4→5(1): dist[4] + 1 = -199 + 1 = -198 < ∞ → 更新 dist[5] = -198
第二次松弛
- 边
1→2(100): 0 + 100 = 100 = 100 → 无变化 - 边
1→3(1): 0 + 1 = 1 > -200 → 无变化 - 边
2→3(-300): 100 - 300 = -200 = -200 → 无变化 - 边
3→4(1): -200 + 1 = -199 = -199 → 无变化 - 边
4→5(1): -199 + 1 = -198 = -198 → 无变化
......
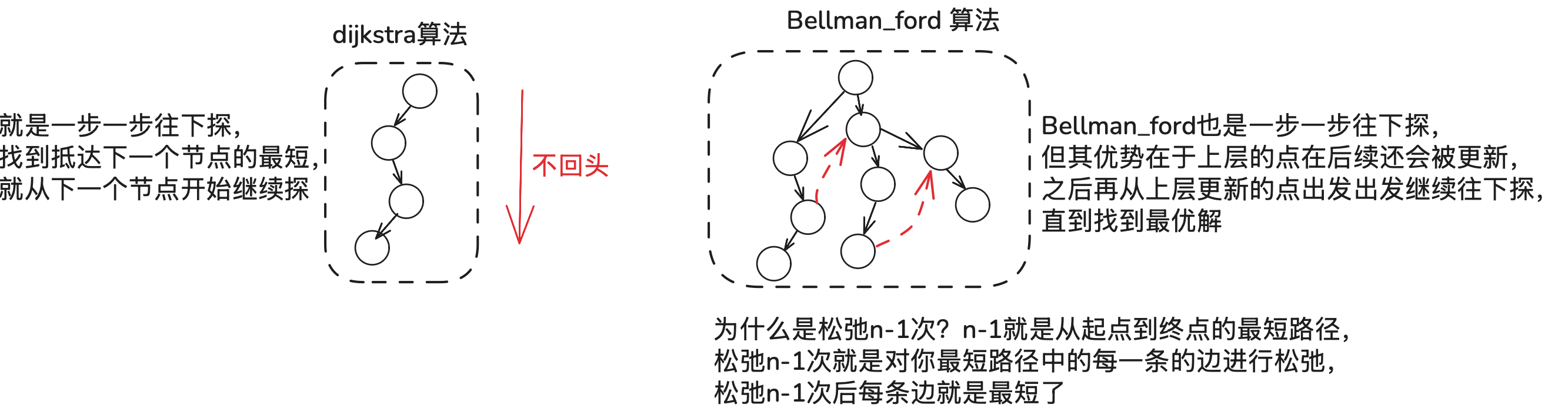
经过4次松弛后就得到了更新后的min_List数组。从树的生成角度来理解这两个算法,如下:
Code
if __name__ == "__main__":city_size, road_size = map(int, input().split())length = city_size + 1graph = [[] for _ in range(length)] ##graph 存储了length个空数组min_List = [float('inf')] * lengthmin_List [1] = 0for _ in range(road_size):s, t, v = map(int, input().split())graph[s].append([t,v])for _ in range(city_size): ## 松弛n-1次updated = False ## 不一定要松弛完n-1次,如果发现不再更新了,那就可以退出了for i in range(1, length): ## 遍历每个点cur_node = i if len(graph[i]) == 0: ## 没有下一个节点 continuefor j in range(len(graph[i])): ## 每个节点进行了n-1次循环。即n-1次松弛next_node = graph[i][j][0]value = graph[i][j][1]dis = min_List[cur_node] + value # 从起点出发经历当前节点到下一个节点if min_List[cur_node] != float('inf') and dis < min_List[next_node]:min_List[next_node] = disupdated = Trueif updated == False: # 在一次松弛过程中,遍历完所有节点后发现min_List没有更新break if min_List[-1] == float('inf'):print("unconnected")else:print(min_List[-1])注意:非常重要的点:
- 松弛是外循环,遍历节点在内循环。
- 一次松弛是对每个节点之间的边关系进行松弛,而不是一次松弛对当前节点下的所有边关系进行松弛,要搞清楚这二者的区别。
前者才是在找最优解,后者问题很大,看似像dijkstra算法,dijkstra算法是每次选择当前距离最小的未访问节点去进行遍历,后者现在的问题是最短路径一定要是按编号顺序走去得到吗?如下图:
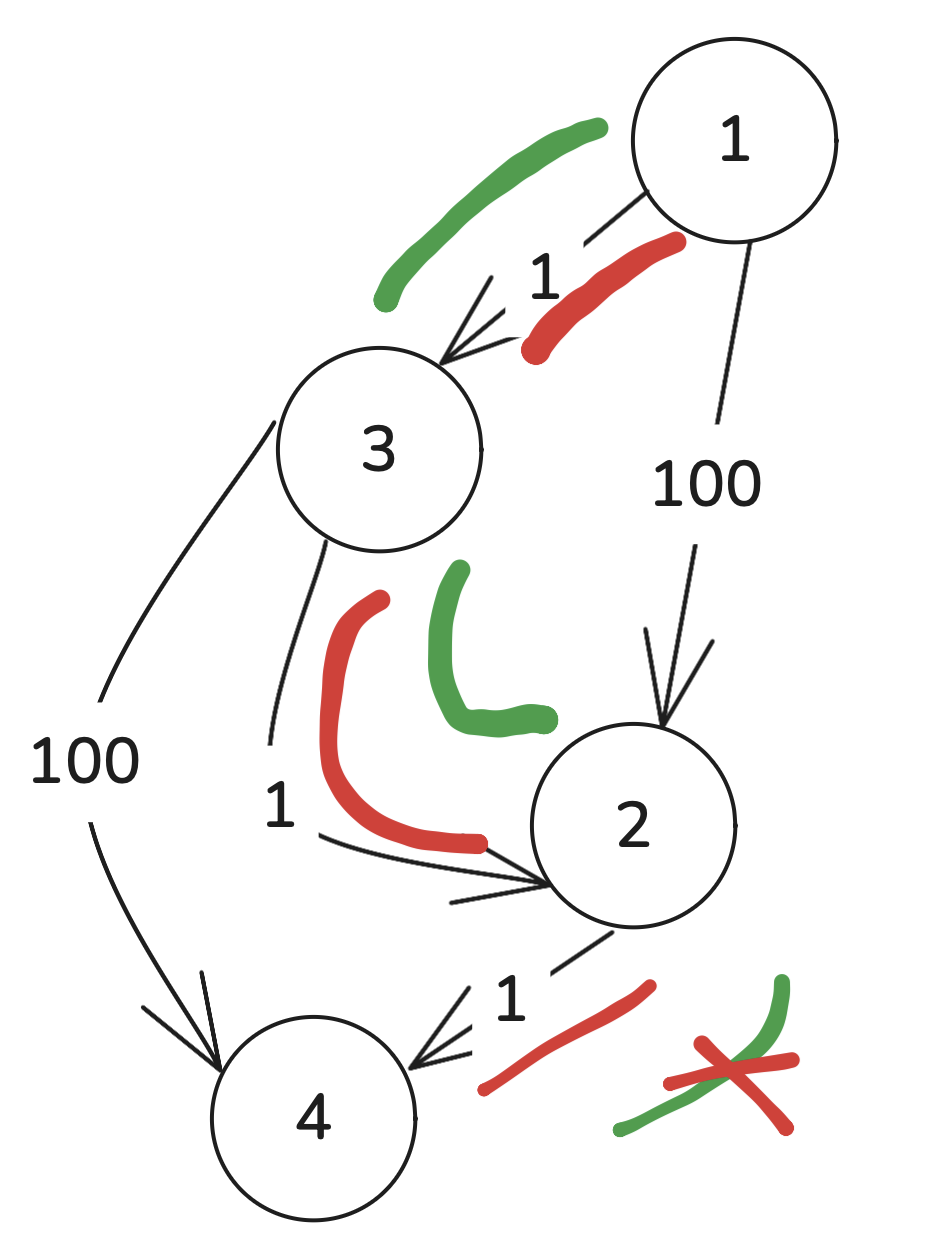
正确路径应该是1-3-2,后者是顺序遍历节点,当遍历到3时,此时虽然能更新节点2的min_List值,但由于后续你不会再去遍历节点2了,因此找不到最优解。
