当前位置：首页 > news >正文

【LeetCode热题100道笔记+动画】最大子数组和

news 2025/8/24 8:53:27

题目描述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

示例 1：
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：
输入：nums = [1]
输出：1

示例 3：
输入：nums = [5,4,-1,7,8]
输出：23

提示：
1 <= nums.length <= 105
-104 <= nums[i] <= 104

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

思考一（动态规划）

以每个元素为结尾的最大子数组和，可通过两种选择确定：要么将当前元素加入前一个子数组（即 dp[i-1] + nums[i]），要么以当前元素为起点重新构建子数组（即 nums[i]），取两者较大值作为 dp[i]。遍历数组时同步更新全局最大值，最终即为结果。

代码

/*** @param {number[]} nums* @return {number}*/
var maxSubArray = function(nums) {let dp = Array(nums.length).fill(0); // dp[i] 表示第个数结尾子数组的最大子数组和dp[0] = nums[0];let ans = nums[0];for (let i = 1; i < nums.length; i++) {dp[i] = Math.max(dp[i-1] + nums[i], nums[i]);ans = Math.max(ans, dp[i]);}return ans;
};

优化

动态规划中无需存储所有位置的子数组和，只需保留上一个位置结尾的最大子数组和（maxVal），即可递推当前位置的结果。通过这种滚动更新的方式，空间复杂度可从 $O (n)$ 优化至 $O (1)$ 。

代码（动态规划优化）

/*** @param {number[]} nums* @return {number}*/
var maxSubArray = function(nums) {let ans = nums[0], maxVal = nums[0]; // ans记录全局最大和，maxVal记录上一位置结尾的最大和for (let i = 1; i < nums.length; i++) {maxVal = Math.max(maxVal + nums[i], nums[i]); // 递推当前位置的最大和ans = Math.max(ans, maxVal); // 更新全局最大值}return ans;
};

思考二（分治法）

分治法求解最大子数组和的核心思路是：将原数组递归分解为更小的子数组，分别求解每个子数组的最大和，再通过合并子问题的解得到原问题的答案。

具体来说，数组的最大子数组只有三种可能：要么完全在左半部分，要么完全在右半部分，要么横跨左右两部分（包含中间元素）。因此，递归过程中只需计算这三种情况的最大值，即可得到当前数组的最大子数组和。该方法的难点在于准确计算“横跨左右的最大子数组和”，以及处理递归的边界条件。

算法过程

分解：
将当前数组区间 [left, right] 以枢轴 pivot（中间位置）分为左子数组 [left, pivot-1] 和右子数组 [pivot+1, right]，递归求解左右子数组的最大子数组和（分别记为 leftMax 和 rightMax）。
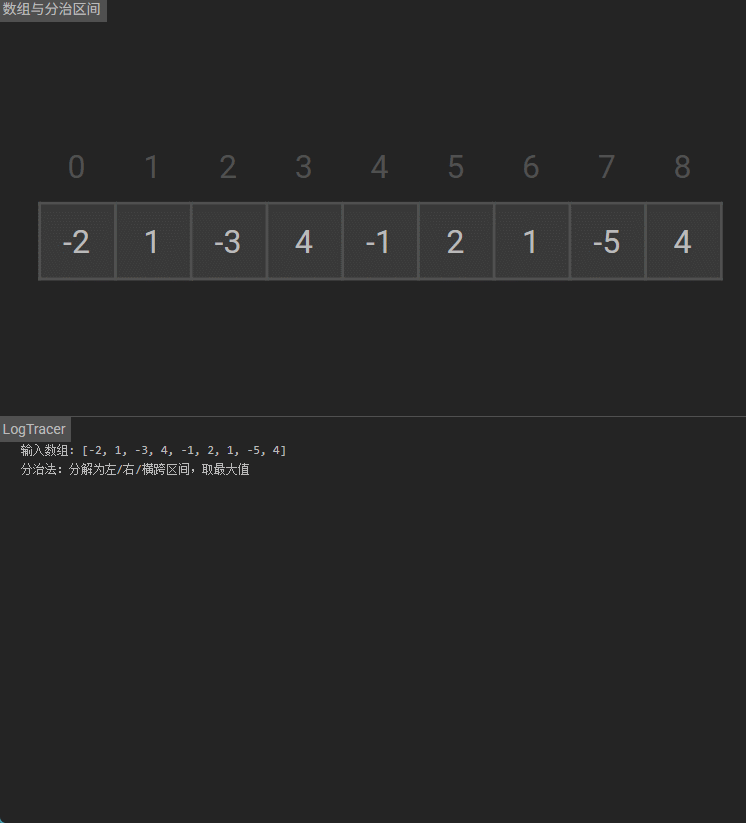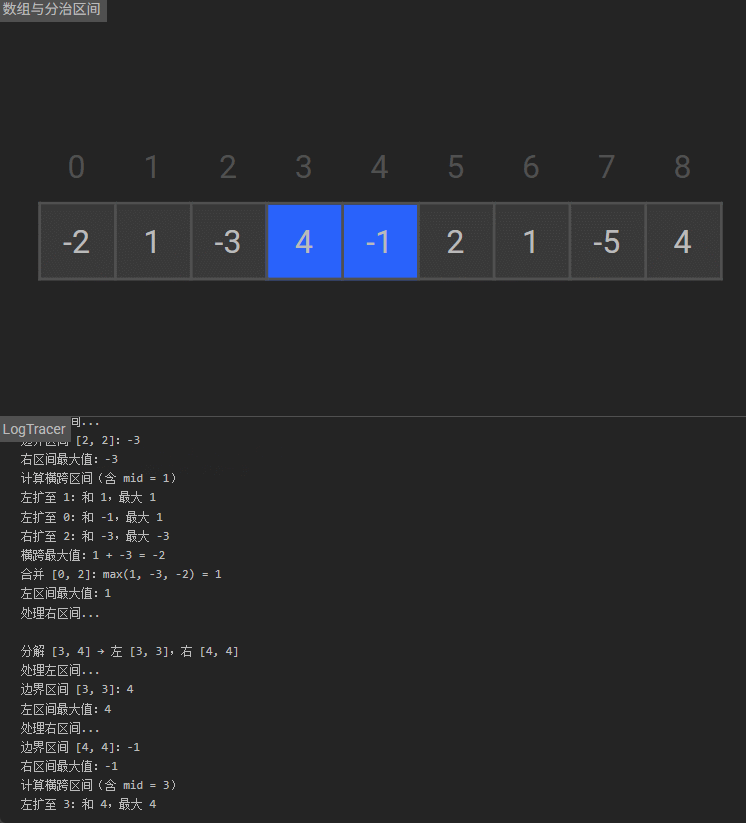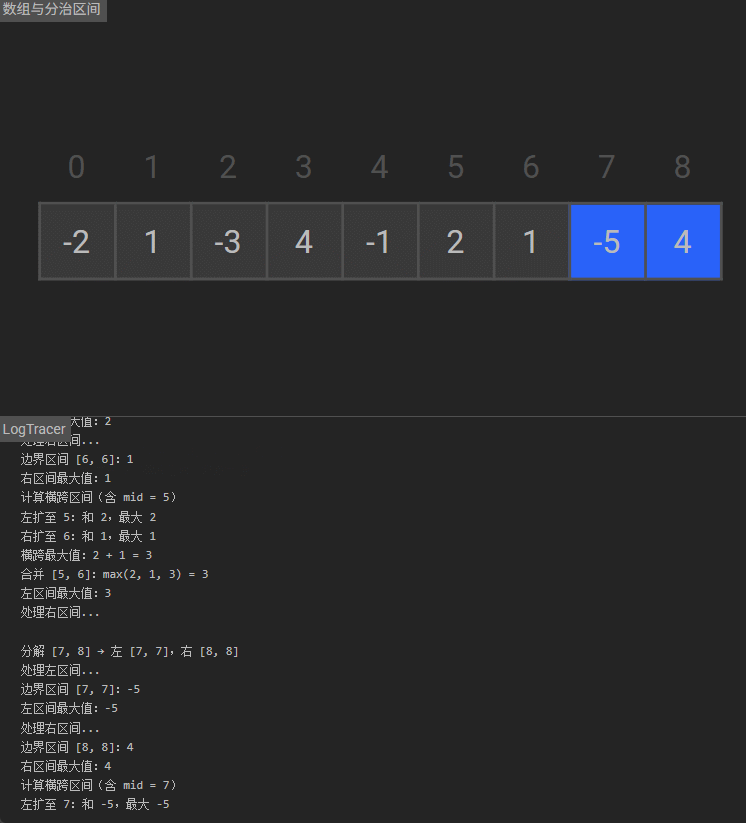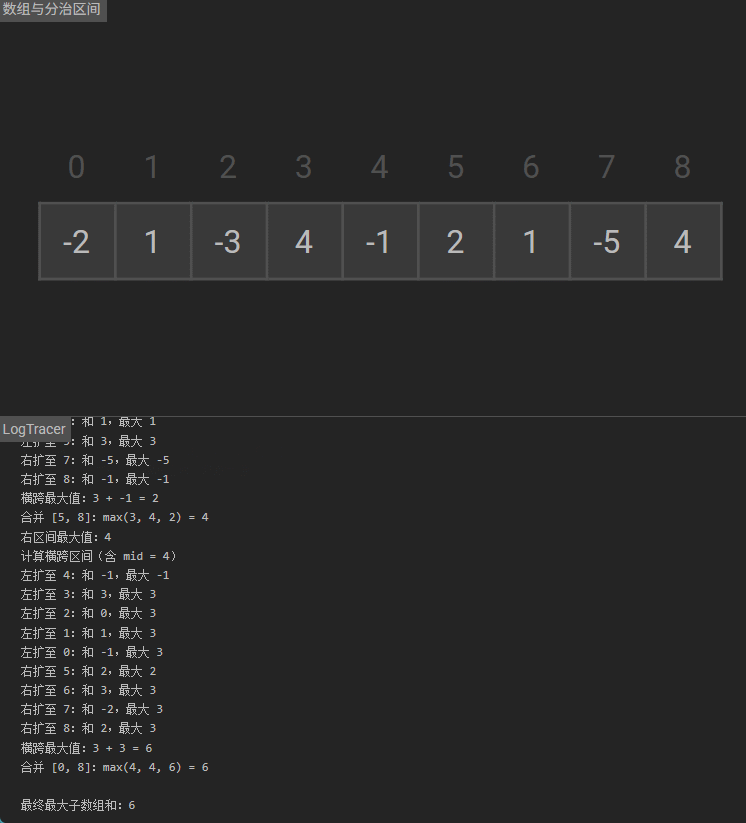
求解横跨左右的最大子数组和：
从枢轴 pivot 向左侧扩展，计算包含枢轴的左半部分最大和（即从枢轴向左累加，取过程中的最大值）；
从枢轴 pivot 向右侧扩展，计算包含枢轴的右半部分最大和；
两者相加（若右半部分最大和为正，否则只取左半部分），得到横跨左右的最大和 middleMax。
合并：
当前数组的最大子数组和为 leftMax、rightMax、middleMax 中的最大值，作为递归返回结果。
边界条件：
当子数组长度为1时（left == right），最大和即为该元素本身。

代码

/*** @param {number[]} nums* @return {number}*/
var maxSubArray = function(nums) {const len = nums.length;if (len === 1) {return nums[0];}const divideAndConquer = function(left, pivot, right) {// 处理枢轴左边子数组let leftMax = -Infinity;if (pivot - left <= 1) { // 左边数组就包含一个元素leftMax = nums[left];} else {leftMax = divideAndConquer(left, left + Math.floor((pivot-left)/2), pivot);}// 处理枢轴右边子数组let rightMax = -Infinity;if (right -pivot <= 1) {// 右边数组就包含一个元素rightMax = nums[right];} else {rightMax = divideAndConquer(pivot, pivot + Math.floor((right - pivot)/2), right);}// 处理中间跨左右子数组的部分（包含pivot）let middleMax = nums[pivot];let maxVal = nums[pivot];for (let i = pivot-1; i >= left; i--) {maxVal += nums[i];middleMax = Math.max(middleMax, maxVal);}maxVal = 0;let sumRight = 0;for (let i = pivot+1; i <= right; i++) {maxVal += nums[i];sumRight = Math.max(sumRight, maxVal);}if (sumRight > 0) {middleMax += sumRight;}return Math.max(leftMax, middleMax, rightMax);};return divideAndConquer(0, Math.floor(len/2), len-1);    
};