代码随想录Day59:图论(最短路算法dijkstra堆优化版精讲、Bellman_ford 算法精讲)
一、实战
dijkstra堆优化版精讲
47. 参加科学大会(第六期模拟笔试)
dijkstra基础版见文章https://blog.csdn.net/m0_73724472/article/details/150577059?spm=1001.2014.3001.5502![]() https://blog.csdn.net/m0_73724472/article/details/150577059?spm=1001.2014.3001.5502
https://blog.csdn.net/m0_73724472/article/details/150577059?spm=1001.2014.3001.5502
朴素版的dijkstra时间复杂度为 O(n^2),只和 n (节点数量)有关系。如果n的数量进一步上升,可以换一个角度来优先性能。
在最小生成树章节涉及两个算法,prim算法(从点的角度来求最小生成树)、Kruskal算法(从边的角度来求最小生成树)。朴素dijkstra当时是从点出发,也就是类似prim算法,那我们也可以想到如果点多边少(这里的多少都是相对而言),是不是可以从边的角度进行优化。
图的存储:主流两种方式邻接矩阵和邻接表
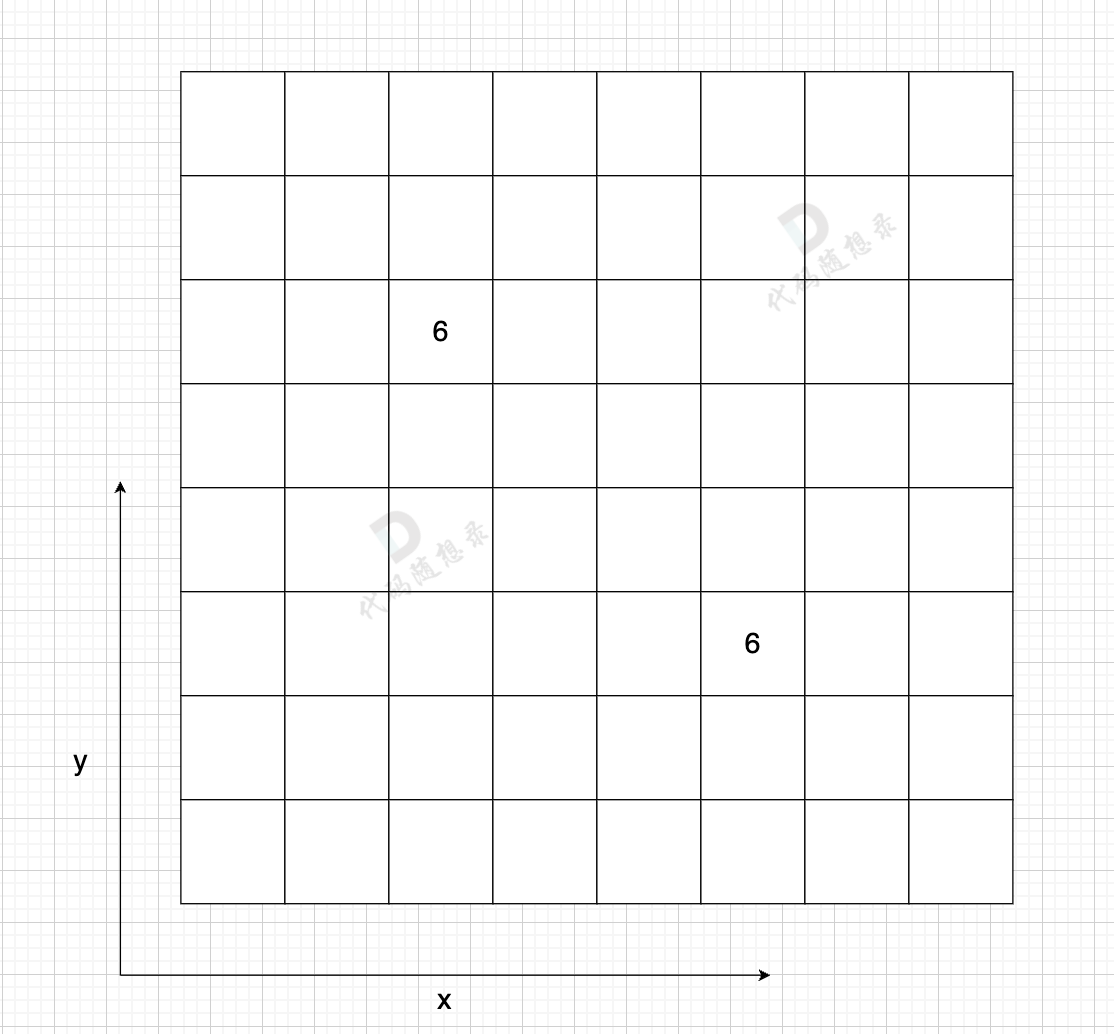
- 表达方式简单,易于理解
- 检查任意两个顶点间是否存在边的操作非常快
- 适合稠密图,在边数接近顶点数平方的图中,邻接矩阵是一种空间效率较高的表示方法。
缺点:
- 遇到稀疏图(点多边少),会导致申请过大的二维数组造成空间浪费 且遍历 边 的时候需要遍历整个n * n矩阵,造成时间浪费
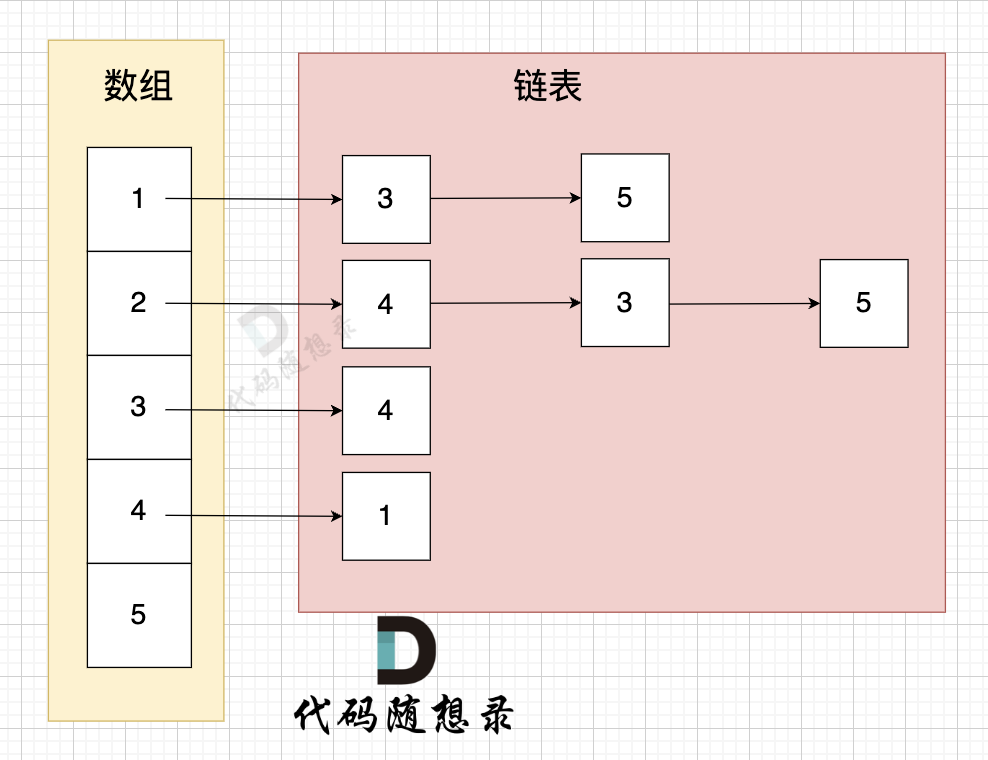
这里表达的图是:
- 节点1 指向 节点3 和 节点5
- 节点2 指向 节点4、节点3、节点5
- 节点3 指向 节点4,节点4指向节点1。
邻接表的优点:
- 对于稀疏图的存储,只需要存储边,空间利用率高
- 遍历节点链接情况相对容易
缺点:
- 检查任意两个节点间是否存在边,效率相对低,需要 O(V)时间,V表示某节点链接其他节点的数量。
- 实现相对复杂,不易理解
本题既然打算从边的方向进行突破,那这里的情况就更接近于稀疏图,因此我们选择邻接表的存储方式,具体如下。
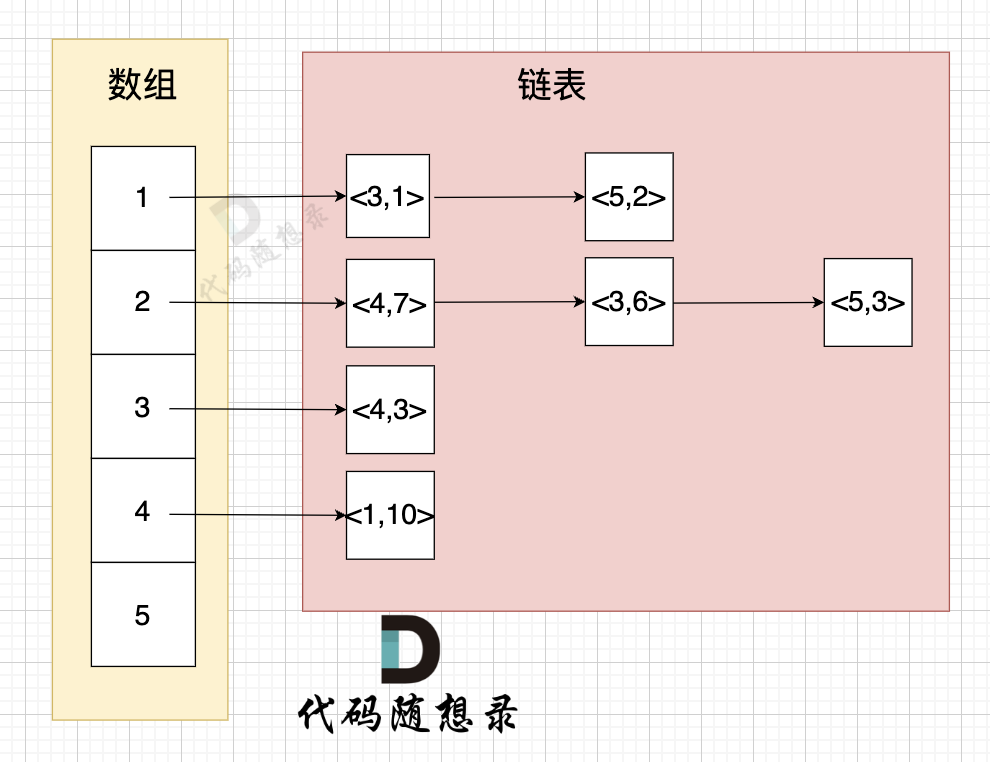
- 节点1 指向 节点3 权值为 1
- 节点1 指向 节点5 权值为 2
- 节点2 指向 节点4 权值为 7
- 节点2 指向 节点3 权值为 6
- 节点2 指向 节点5 权值为 3
- 节点3 指向 节点4 权值为 3
- 节点5 指向 节点1 权值为 10
堆优化细节:
思路依然是 dijkstra 三部曲:
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组)、
之前是 通过遍历节点来遍历边,通过两层for循环来寻找距离源点最近节点。 这次我们直接遍历边,且通过堆来对边进行排序,达到直接选择距离源点最近节点。
第一步中,要选择距离源点近的节点(即:该边的权值最小),所以 我们需要一个 小顶堆 来帮我们对边的权值排序,每次从小顶堆堆顶 取边就是权值最小的边。
第二步、第三步同上,没有变化。
时间复杂度的优化:
- 时间复杂度:O(ElogE) E 为边的数量
- 空间复杂度:O(N + E) N 为节点的数量
堆优化的时间复杂度 只和边的数量有关 和节点数无关,在 优先级队列中 放的也是边。空间复杂度,邻接表是 数组 + 链表 数组的空间 是 N ,有E条边 就申请对应多少个链表节点,所以是 复杂度是 N + E
堆优化dijkstra 中 为什么一定要用邻接表呢,用邻接矩阵 行不行 ?
可以但是没必要。因为稀疏图,所以使用堆优化的思路, 如果还用 邻接矩阵 去表达这个图的话,就是 一个高效的算法 使用了低效的数据结构,那么 整体算法效率 依然是低的。
package org.example;import java.util.*;class Edge {int to; // 邻接顶点int val; // 边的权重Edge(int to, int val) {this.to = to;this.val = val;}
}//比较两个 (城市, 距离),按距离从小到大排
// 比如(城市2, 距离5) 比 (城市3, 距离10) 更近,所以优先处理更近的城市
class MyComparison implements Comparator<Pair<Integer, Integer>> {@Overridepublic int compare(Pair<Integer, Integer> lhs, Pair<Integer, Integer> rhs) {return Integer.compare(lhs.second, rhs.second);}
}class Pair<U, V> {public final U first;public final V second;public Pair(U first, V second) {this.first = first;this.second = second;}
}public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(); // 城市数量int m = scanner.nextInt(); // 路的数量List<List<Edge>> grid = new ArrayList<>(n + 1);for (int i = 0; i <= n; i++) {grid.add(new ArrayList<>());}for (int i = 0; i < m; i++) {int p1 = scanner.nextInt(); // 起点城市int p2 = scanner.nextInt(); // 终点城市int val = scanner.nextInt(); // 路的长度grid.get(p1).add(new Edge(p2, val));}int start = 1; // 起点int end = n; // 终点// 存储从源点到每个节点的最短距离int[] minDist = new int[n + 1];Arrays.fill(minDist, Integer.MAX_VALUE);// 记录顶点是否被访问过boolean[] visited = new boolean[n + 1];// 优先队列中存放 Pair<节点,源点到该节点的权值>PriorityQueue<Pair<Integer, Integer>> pq = new PriorityQueue<>(new MyComparison());// 初始化队列,源点到源点的距离为0,所以初始为0pq.add(new Pair<>(start, 0));minDist[start] = 0; // 起始点到自身的距离为0while (!pq.isEmpty()) {// 第一步,选源点到哪个节点近且该节点未被访问过(通过优先级队列来实现)// <节点, 源点到该节点的距离>Pair<Integer, Integer> cur = pq.poll();if (visited[cur.first]) continue;// 第二步,该最近节点被标记访问过visited[cur.first] = true;// 第三步,更新非访问节点到源点的距离(即更新minDist数组)for (Edge edge : grid.get(cur.first)) { // 遍历 cur指向的节点,cur指向的节点为 edge// cur指向的节点edge.to,这条边的权值为 edge.valif (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDistminDist[edge.to] = minDist[cur.first] + edge.val;pq.add(new Pair<>(edge.to, minDist[edge.to]));}}}if (minDist[end] == Integer.MAX_VALUE) {System.out.println(-1); // 不能到达终点} else {System.out.println(minDist[end]); // 到达终点最短路径}}
}
Bellman_ford 算法精讲
94. 城市间货物运输 I
之前有提到dijkstra的限制——在有边为负数的情况下无法使用
Bellman_ford 算法就是为了解决经典的带负权值的单源最短路问题
该算法是由 R.Bellman 和L.Ford 在20世纪50年代末期发明的算法,故称为Bellman_ford算法
核心思想:对所有边进行松弛n-1次操作(n为节点数量),从而求得目标最短路。
什么是松弛?(Bellman_ford算法的核心操作)
举个例子,每条边有起点、终点和边的权值。例如一条边,节点A 到 节点B 权值为value,如图:
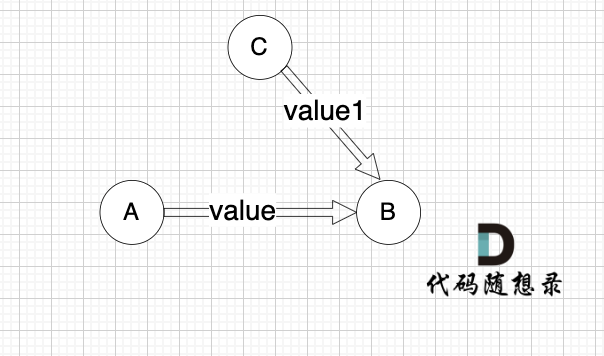
minDist[B] 表示 到达B节点 最小权值,minDist[B] 有哪些状态可以推出来?
状态一: minDist[A] + value 可以推出 minDist[B]
状态二: minDist[B]本身就有权值 (可能是其他边链接的节点B 例如节点C,以至于 minDist[B]记录了其他边到minDist[B]的权值)
minDist[B] 应如何取舍?本题要求最小权值,那么 这两个状态我们就取最小的
if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value也就是说,如果 通过 A 到 B 这条边可以获得更短的到达B节点的路径,即如果 minDist[B] > minDist[A] + value,那么我们就更新 minDist[B] = minDist[A] + value ,这个过程就叫做 “松弛” 。
为什么是 n - 1次 松弛呢?
模拟一遍过程,使用minDist数组来表达 起点到各个节点的最短距离,例如minDist[3] = 5 表示起点到达节点3 的最小距离为5。
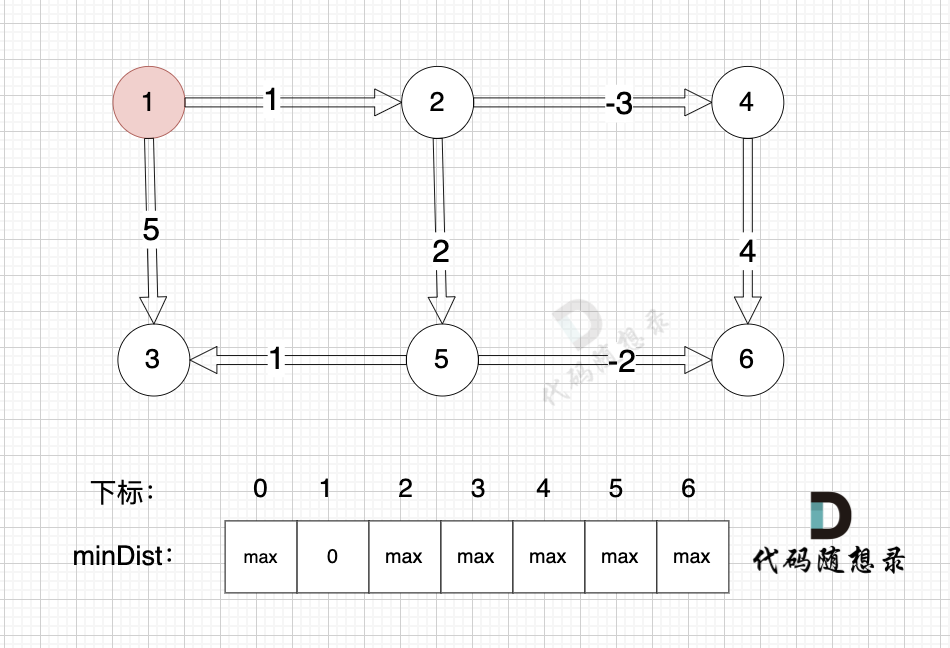
示例给出的所有边为例:
5 6 -2
1 2 1
5 3 1
2 5 2
2 4 -3
4 6 4
1 3 5
接下来松弛一遍所有的边。
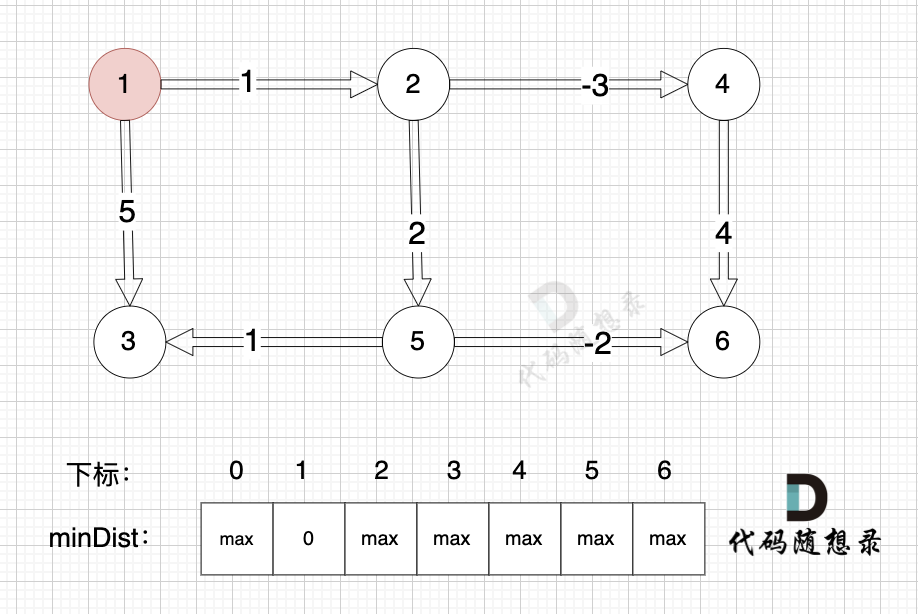
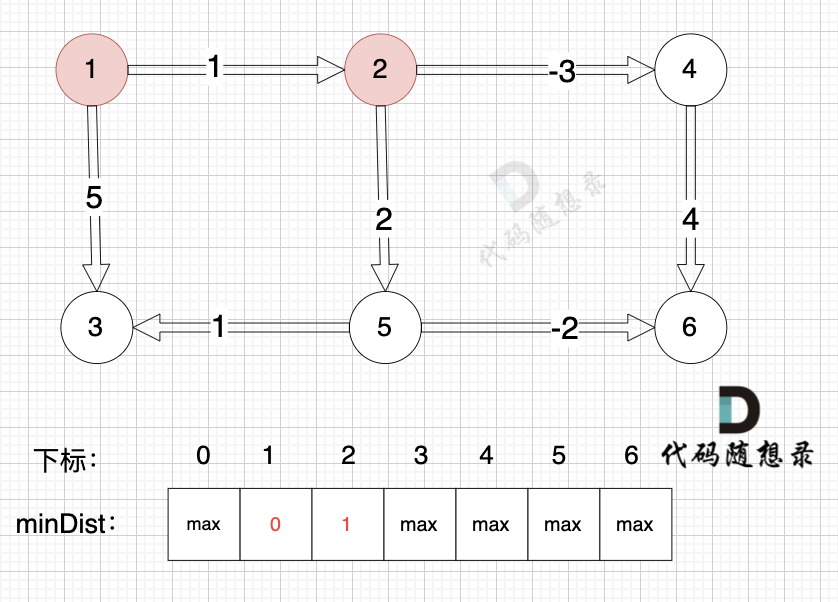
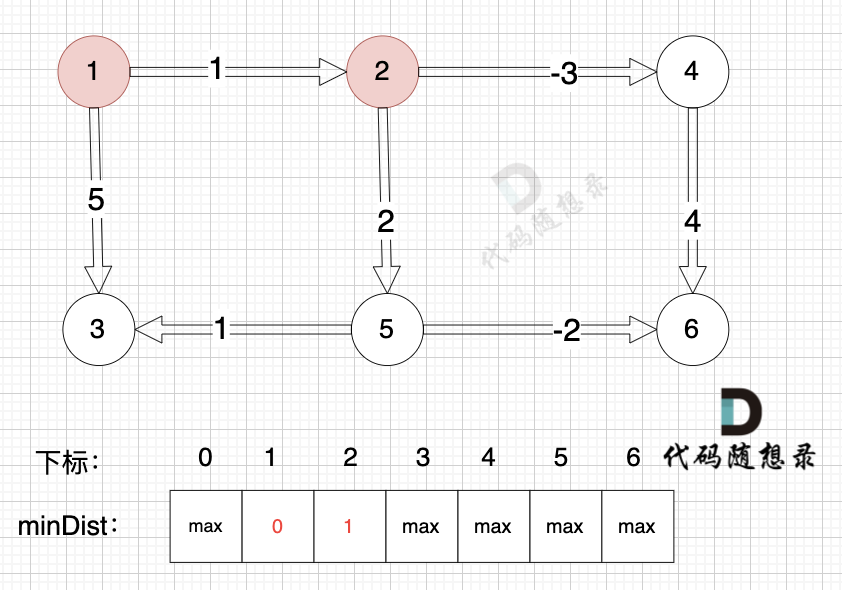
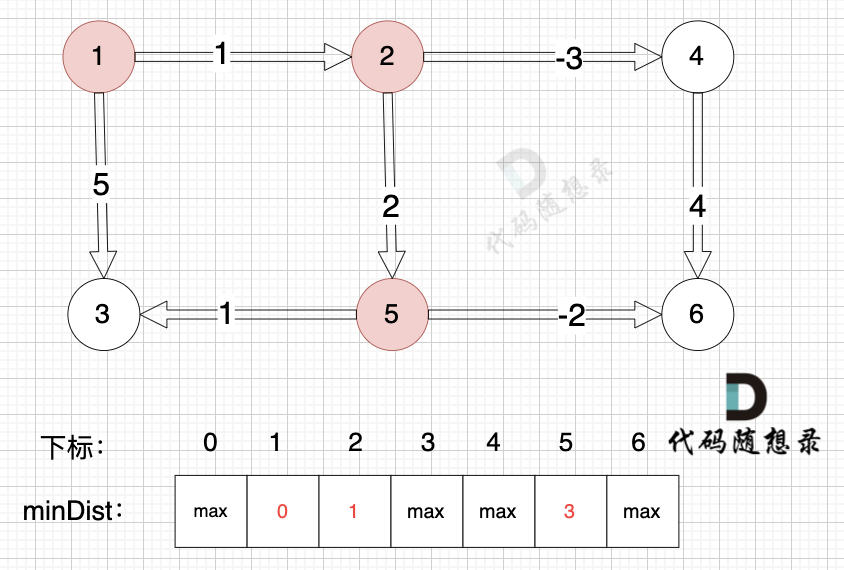
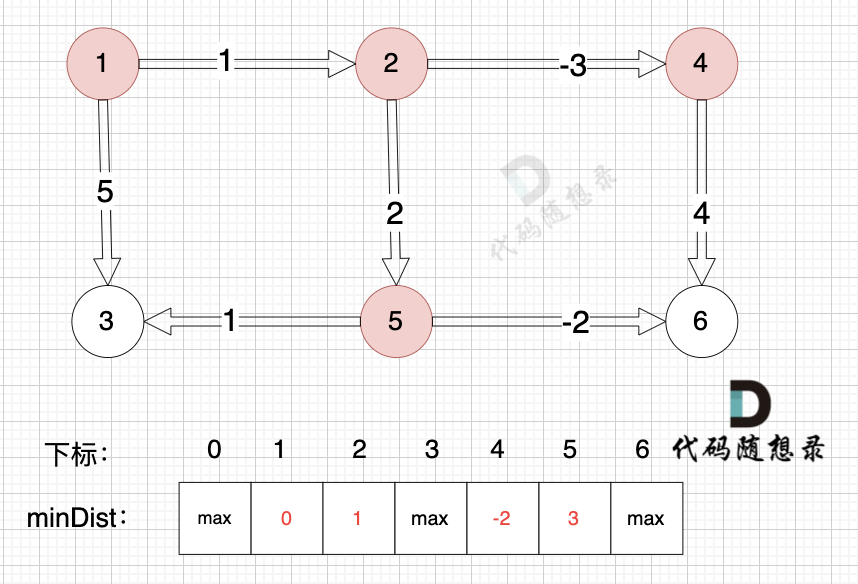
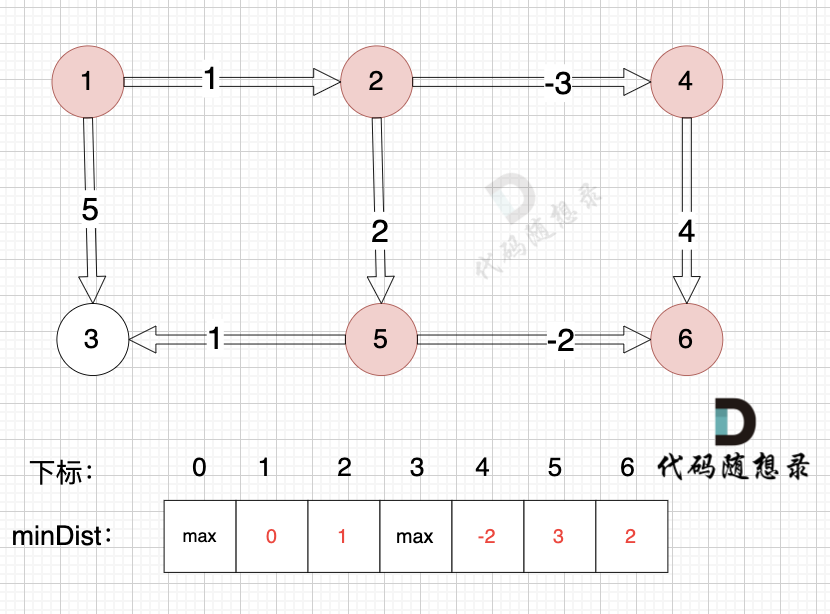
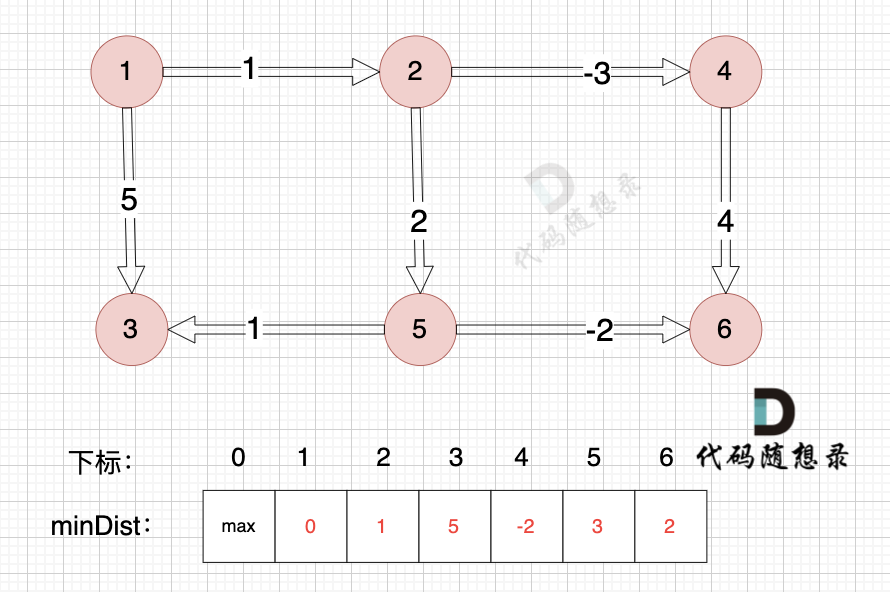
以上是对所有边进行一次松弛之后的结果。那么需要对所有边松弛几次才能得到 起点(节点1) 到终点(节点6)的最短距离呢?对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离。上面的距离中,我们得到里 起点达到 与起点一条边相邻的节点2 和 节点3 的最短距离,分别是 minDist[2] 和 minDist[3]。这里有疑惑,minDist[3] = 5,分明不是 起点到达 节点3 的最短距离,节点1 -> 节点2 -> 节点5 -> 节点3 这条路线 距离才是4。
注意上面讲的是 对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离,这里 说的是 一条边相连的节点。
与起点(节点1)一条边相邻的节点,到达节点2 最短距离是 1,到达节点3 最短距离是5。而 节点1 -> 节点2 -> 节点5 -> 节点3 这条路线 是 与起点 三条边相连的路线了。所以对所有边松弛一次 能得到 与起点 一条边相连的节点最短距离。那对所有边松弛两次 可以得到与起点 两条边相连的节点的最短距离。那对所有边松弛三次 可以得到与起点 三条边相连的节点的最短距离,这个时候,我们就能得到到达节点3真正的最短距离,也就是 节点1 -> 节点2 -> 节点5 -> 节点3 这条路线。
那么再回归刚刚的问题,需要对所有边松弛几次才能得到 起点(节点1) 到终点(节点6)的最短距离呢?节点数量为n,那么起点到终点,最多是 n-1 条边相连。那么无论图是什么样的,边是什么样的顺序,我们对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。
Bellman_ford 的核心算法思路共有以上两个关键点。
- “松弛”究竟是个啥?
- 为什么要对所有边松弛 n - 1 次 (n为节点个数) ?
package org.example;import java.util.*;public class Main {// 定义一个内部类 Edge,用于表示边的信息:起点、终点和权重static class Edge {int from; // 边的起点int to; // 边的终点int val; // 边的权重(距离)public Edge(int from, int to, int val) {this.from = from;this.to = to;this.val = val;}}public static void main(String[] args) {// 输入处理Scanner sc = new Scanner(System.in);int n = sc.nextInt(); // 城市数量(节点数)int m = sc.nextInt(); // 道路数量(边数)List<Edge> edges = new ArrayList<>(); // 存储所有的边// 读取所有边的信息for (int i = 0; i < m; i++) {int from = sc.nextInt(); // 起点城市int to = sc.nextInt(); // 终点城市int val = sc.nextInt(); // 边的权重(距离)edges.add(new Edge(from, to, val)); // 将边加入列表}// minDist[i] 表示从起点到城市 i 的最短距离int[] minDist = new int[n + 1];// 初始化 minDist 数组,所有城市的初始距离设为无穷大Arrays.fill(minDist, Integer.MAX_VALUE);minDist[1] = 0; // 起点到自身的距离为 0// 开始松弛操作,更新最短路径for (int i = 1; i < n; i++) { // 进行 n-1 次松弛操作for (Edge edge : edges) { // 遍历所有边// 如果当前边的起点的距离不是无穷大,并且通过该边可以找到更短的路径if (minDist[edge.from] != Integer.MAX_VALUE && (minDist[edge.from] + edge.val) < minDist[edge.to]) {// 更新目标城市的最短距离minDist[edge.to] = minDist[edge.from] + edge.val;}}}// 输出结果if (minDist[n] == Integer.MAX_VALUE) {System.out.println("unconnected"); // 如果终点不可达,输出 "unconnected"} else {System.out.println(minDist[n]); // 输出从起点到终点的最短距离}}
}