数据结构之排序大全(2)
选择排序
直接选择排序
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
直接选择排序的思路很简单:
我们先从数组中找到最小的元素,它应该放在数组中的第一个位置,然后再从剩下的元素中找到最小的元素,把它放到第二个位置,以此类推,最后整个数组就是从小到大进行排列的了。
那我们就来写一下代码:
//直接选择排序
void SelectSort(int* arr, int n)
{for (int i = 0; i < n; i++){//假设数组中最小的元素就是mini指向的元素int mini = i;for (int j = i + 1; j < n; j++){if (arr[mini] > arr[j]){//找到待排序列中最小的元素mini = j;}}swap(&arr[i], &arr[mini]);}
}
我们可以很快的得出直接选择排序的时间复杂度是O(N^2)。
我们上面是每次找到最小值并将它往前面放,那有没有什么方法对这个代码进行优化呢?
是有的。前面是找待排数据中的最小值往前放,那我们是不是也能与此同时找到待排数据的最大值往后放呢,这样的话,算法所耗费的时间肯定比之前要少,那我们就来写一下代码吧:
void SelectSort1(int* arr, int n)
{int begin = 0;int end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin; i <= end; i++){if (arr[i] < arr[mini]){mini = i;}if (arr[i] > arr[maxi]){maxi = i;}}//交换mini与begin指向的值、maxi与end指向的值swap(&arr[mini], &arr[begin]);swap(&arr[maxi], &arr[end]);begin++;end--;}
}那我们现在来测试一下吧,假设我们要测试的序列为{9 8 7 6 5 4 3 2 1 0},结果会变成升序的吗?
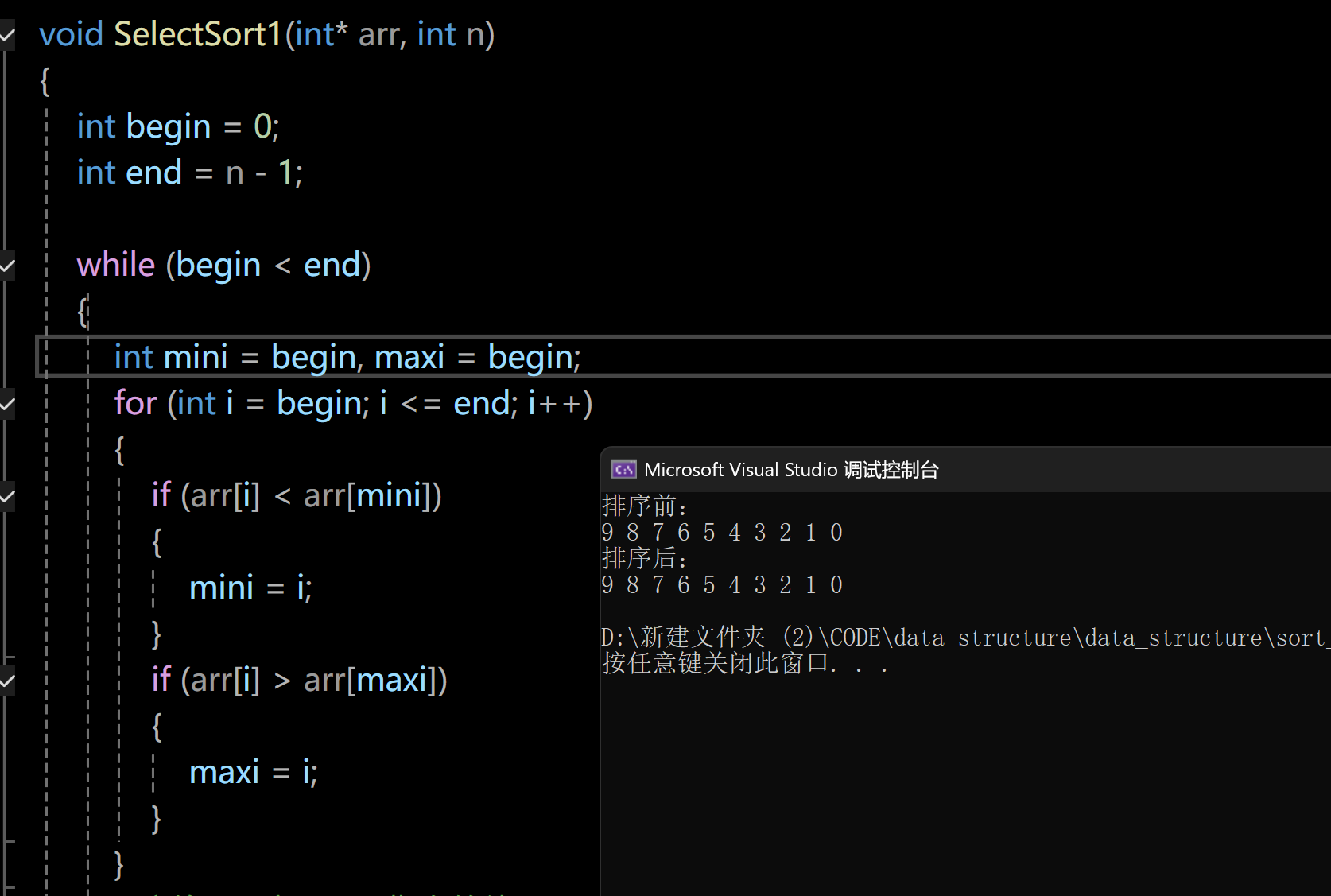
我们可以看到,排序前后数组根本就没有位置上的变化,这是怎么回事呢?我们一起来分析一下:
我们知道,初始时begin,maxi,mini指向的元素是9,end指向的元素是0,经过第一轮找数组中的最大元素和最小元素之后,maxi仍会指向元素9,与begin指向相同,mini则会指向0,与end指向相同。跳出循环后,就需要交换mini与begin位置的值,那么数组中第一个元素就变成了0,最后一个元素就变成了9,但是,现在maxi仍然指向数组的第一个位置且maxi指向的元素变成了0,end仍然指向数组中的最后一个位置,且最后一个位置的元素变成了9,现在还需要发生maxi指向位置的值与end指向位置的值的交换,那么9又回到第一个位置,0又回到最后一个位置,相当于没交换。对于其他的元素,也是这样的情况。
所以,上面的问题就出在当begin和maxi指向相同的位置的时候,mini要先跟begin交换,交换后begin指向的就是最小值,连带着maxi指向的也是最小值,而交换后mini的位置就是最大值,而此时如果再直接交换maxi与end位置的值,就会发生错误,拿着有什么解决方法嘛
既然当begin和maxi指向相同的位置的时候,mini要先跟begin交换,最大值就到了mini的位置,那我们为啥不先让maxi直接走到mini的位置,这样的话,maxi指向的位置存放的值不就还是最大值了嘛,然后再直接交换maxi和end位置的值就好了呀。
那我们就再修改一下代码:
void SelectSort1(int* arr, int n)
{int begin = 0;int end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin; i <= end; i++){if (arr[i] < arr[mini]){mini = i;}if (arr[i] > arr[maxi]){maxi = i;}}//交换mini与begin指向的值、maxi与end指向的值swap(&arr[mini], &arr[begin]);if (maxi == begin)//如果命中if条件,此时mini指向的位置存放的才是最大值{maxi = mini;}swap(&arr[maxi], &arr[end]);begin++;end--;}
}我们再来测试一下代码看是否能够正确完成任务:
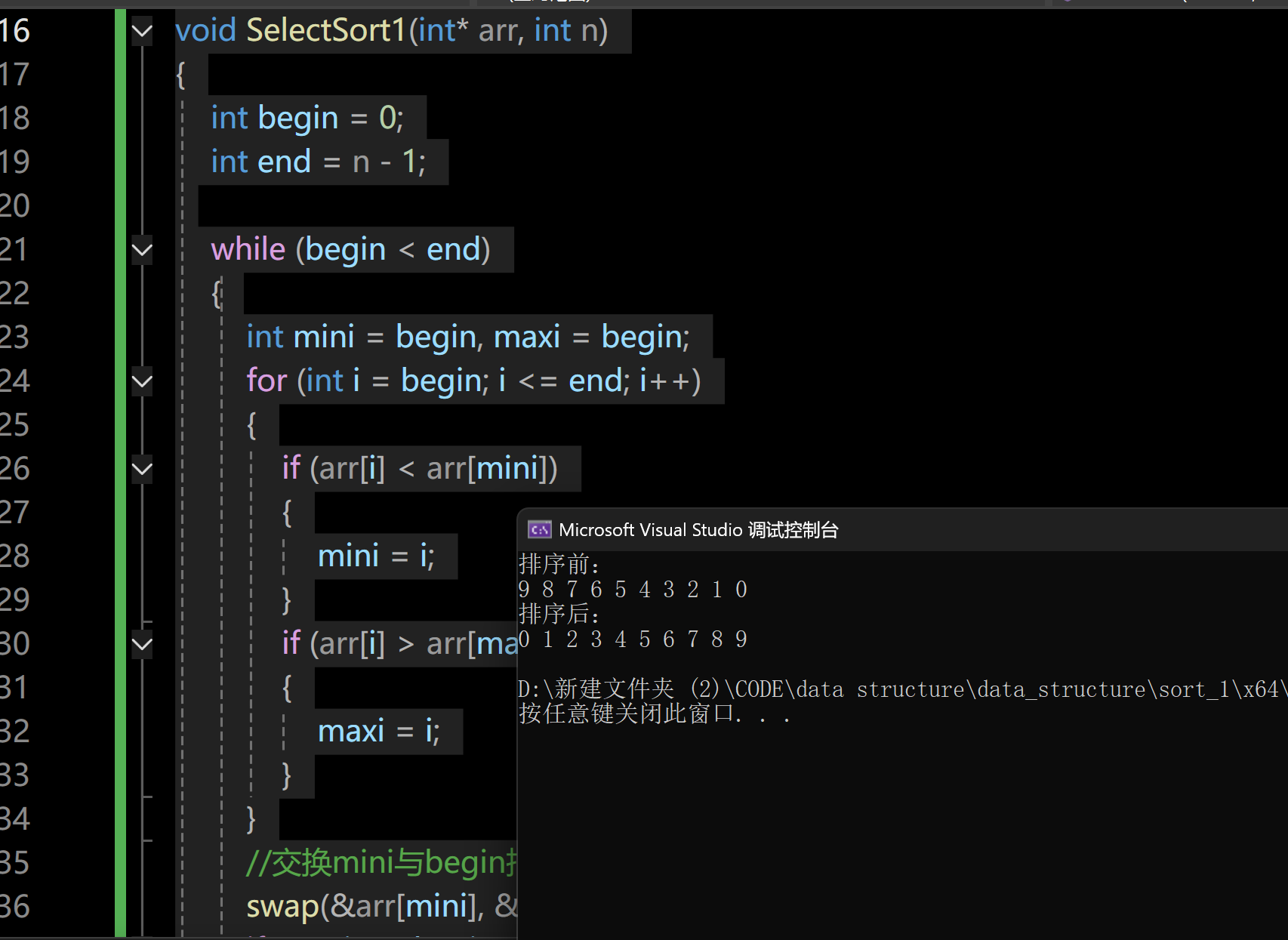
看来修改后代码确实能正确实现任务了。
直接选择排序不管是最坏情况(数组完全倒序)还是最好情况(数组本就有序)都会对整个数组进行遍历去找最大值和最小值,所以时间复杂度都是O(N^2)。
堆排序
对于堆排序,我们有专门一个小节已经讲过了,如果又忘记的小伙伴可以查阅者一篇博客哦:数据结构之堆:完全二叉树的 “优先级管家”,从原理到应用-CSDN博客
我们现在还是再来写一下它的代码:
//堆排序
//交换函数
void swap(int* pa, int* pb)
{int tmp = *pa;*pa = *pb;*pb = tmp;
}
//向下调整算法
void AdjustDown(int* arr, int n, int parent)
{int child = 2 * parent + 1;while (child < n){if (child + 1 < n && arr[child] < arr[child + 1])//此时默认是建立大堆{child++;}if (arr[parent] < arr[child]){swap(&arr[parent], &arr[child]);parent = child;child = 2 * parent + 1;}else{break;}}
}
void HeapSort(int* arr, int n)
{//先将元素建堆——利用向下调整算法//升序建大堆,降序建小堆//这里我们就选择排升序for (int parent = (n - 1 - 1) / 2; parent >= 0; parent--){AdjustDown(arr, n, parent);}//建完堆以后,利用堆结构进行排序for (int size = n - 1; size > 0; size--){swap(&arr[0], &arr[size]);//对剩下的size个元素进行向下调整AdjustDown(arr, size, 0);}
}
堆排序的效率还是比较高的,他的时间复杂度是O(N*logN).
我们也可以通过代码来测试一下这两种算法的时间性能,以下是测试函数:
// 测试排序的性能对⽐
void TestOP()
{//生成随机数,将随机数存入数组srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}//int begin1 = clock();//InsertSort(a1, N);//int end1 = clock();//int begin2 = clock();//ShellSort(a2, N);//int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();//int begin5 = clock();////QuickSort(a5, 0, N - 1);//int end5 = clock();//int begin6 = clock();////MergeSort(a6, N);//int end6 = clock();//int begin7 = clock();//BubbleSort(a7, N);//int end7 = clock();//printf("InsertSort:%d\n", end1 - begin1);//printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);//printf("QuickSort:%d\n", end5 - begin5);//printf("MergeSort:%d\n", end6 - begin6);//printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}看一下运行结果:
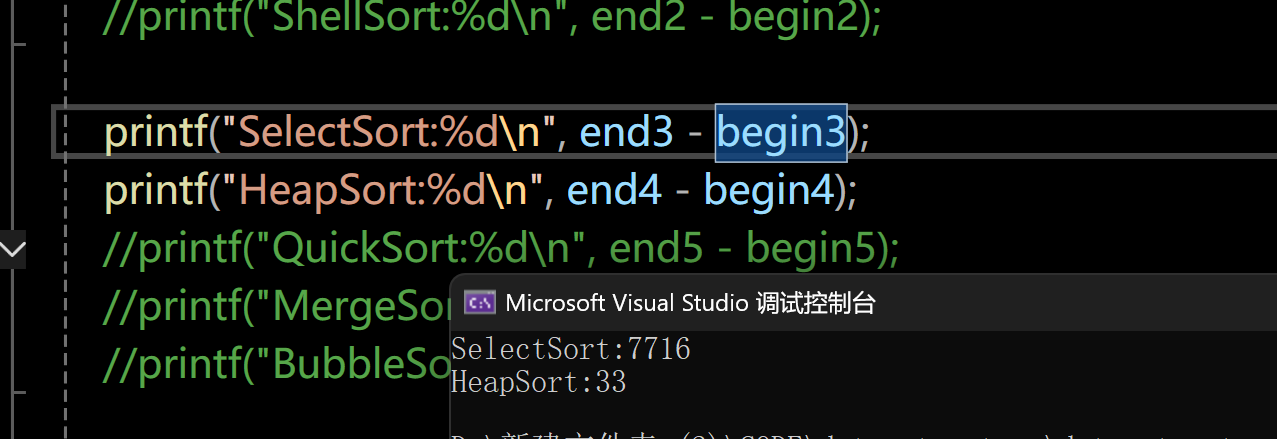
打印出来的结果的单位是毫秒,可以看到,堆排序的时间性能远高于直接选择排序。
总结:这一小节我们主要讲解了选择排序的相关内容,这一小节的内容还是比较简单的,小伙伴们要多加练习。喜欢博主的兄弟们欢迎三连哦,博主会及时更新更多有用的内容的!!
