AVL左旋右旋 学习小得

AVL作为成为二叉搜索树，其本质也是一个二叉平衡树。

作为二叉搜索树，里面的数据是有序的，理想状态下作为成为完美二叉树的时候，按照层序排例是可以拍成顺序的。

二叉平衡树有一个特点，就是左节点的高度和右节点的高度差不能>1。否则这个二叉树就不能成为平衡二叉树。

但是总会有二叉树失衡的时候，这个时候就需要左旋右旋来将二叉树变为平衡二叉树。

而AVL的旋转，就是在不影响其中序遍历（左父右的遍历）的情况下，把失衡的二叉树变为平衡二叉树的过程。

左旋：

使用在右节点高度（最远的子节点，也就是叶节点到根节点的边数）➖左节点的高度>1时

比如：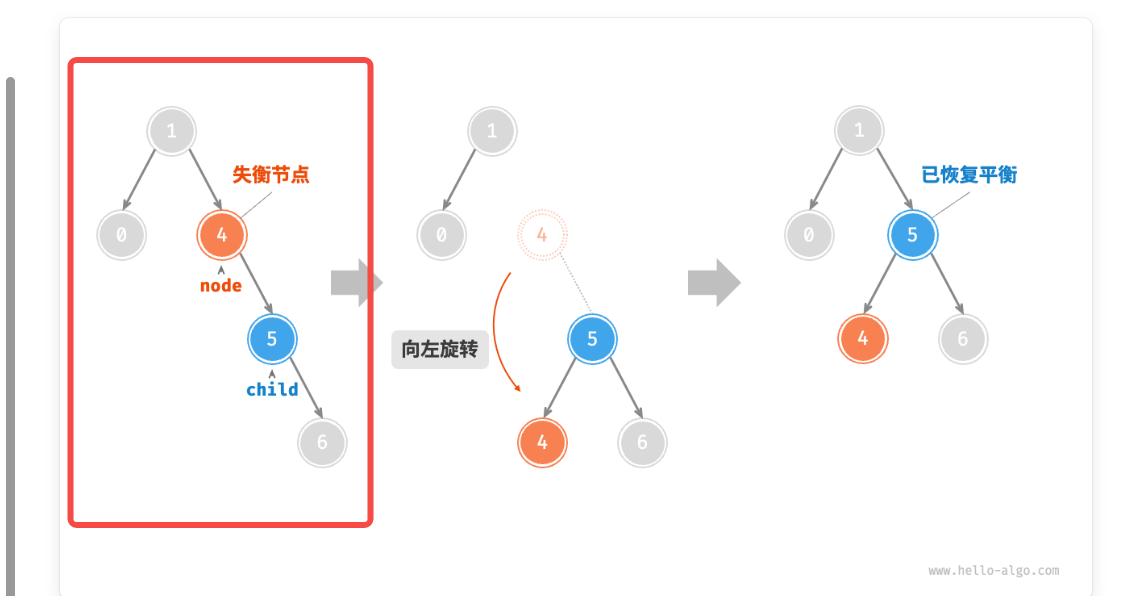

可以看到，1作为根节点时，左节点高度为1，右节点高度为3，3-1>1，所以要左旋。

有个记忆小tips，左旋按照节点中较大的那个为“支点”来进行旋转，这里就是把4以5为支点左旋。

如果4节点有个左节点：

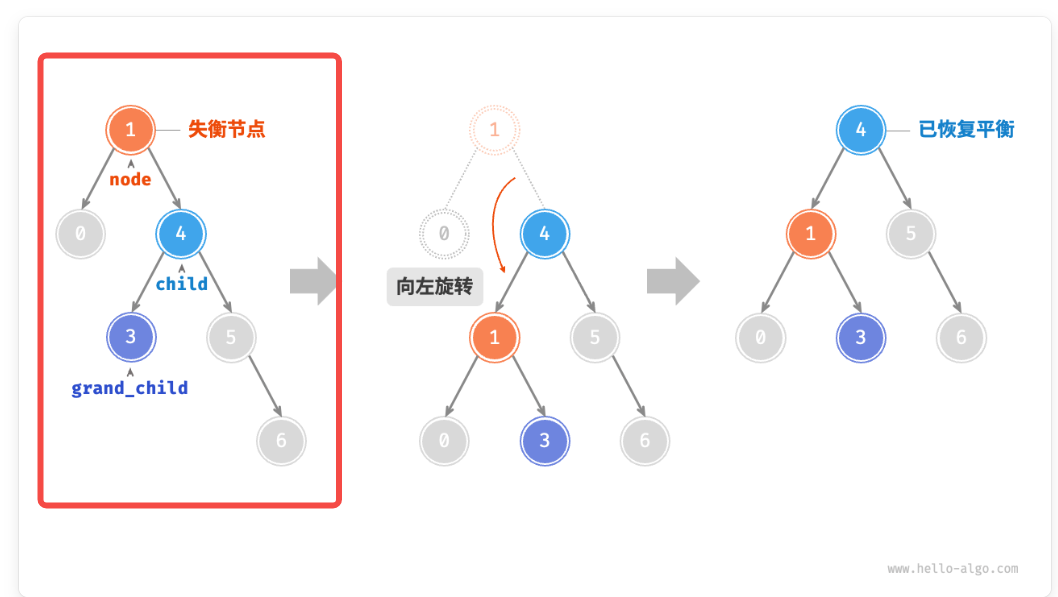
那么4节点的平衡因子就为1，不需要旋转，向上找>1的节点进行旋转。

1节点进行左旋，同时把4节点的左子节点给1节点作为右节点。

右旋

左节点的高度-右节点的高度>1，则该节点需要右旋。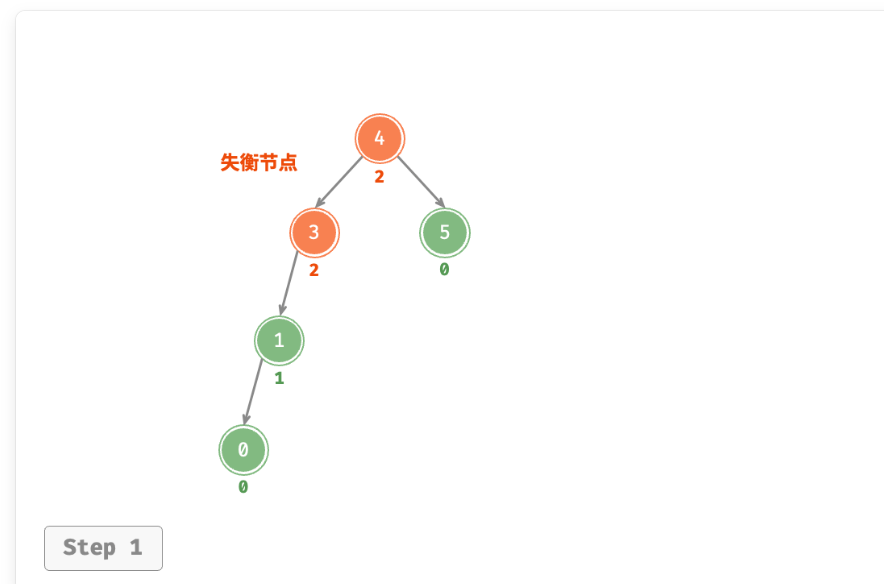

右旋和左旋镜像着来的，右旋时按照小的进行旋转，这里的节点为3，找和他最小的1进行旋转。

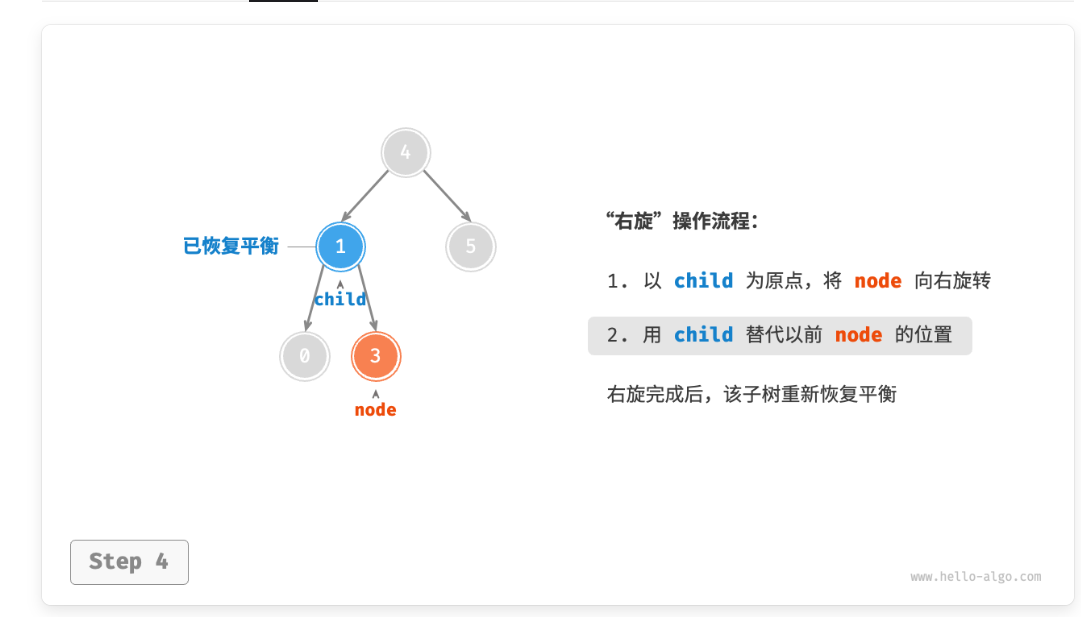
如果原本的3节点有右子节点怎么办？

那么和左旋一样，这里的3的平衡因子就为1，不用旋转，继续向上找，

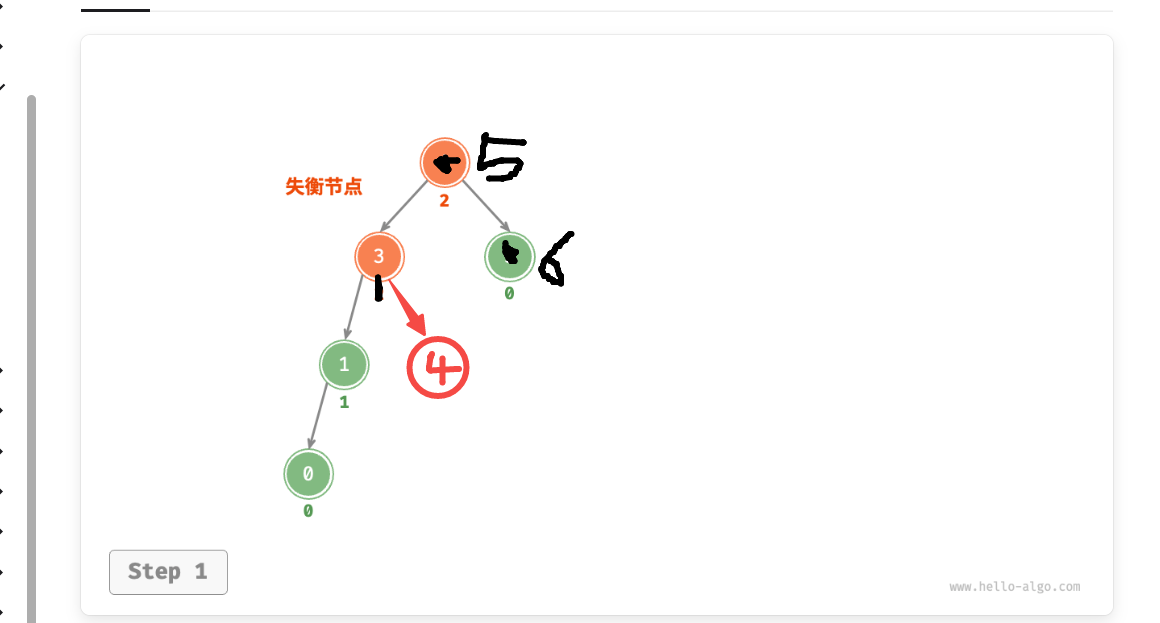
这里要旋转的节点就变为了5，5按照3进行旋转，同时3的右节点给5当左节点

就变为了

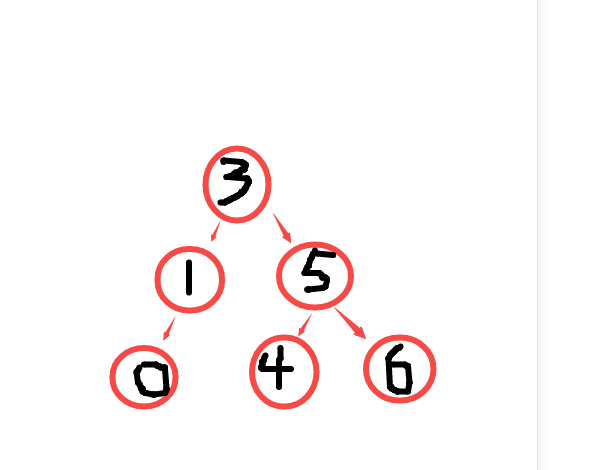
有的需要左旋再右旋，而有的需要右旋再左旋。

比如下图：

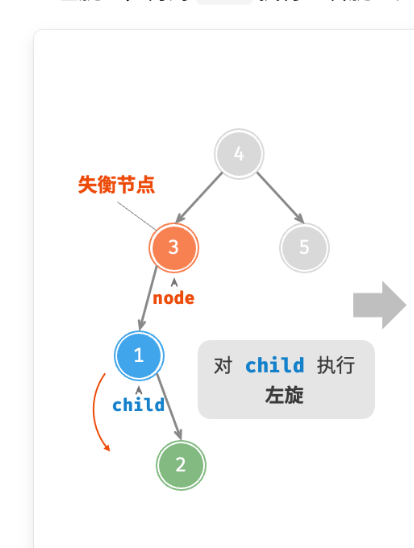
可以看到失衡节点为3，那么此时3的左节点-右节点>1，因此3节点需要右旋，但是1只有右节点（同理，左旋的时候如果右子节点只有左节点也是无法正常旋转的），因此无法对其右旋，这时需要对3节点的左节点进行左旋，将右节点空出来，然后再去进行右旋。

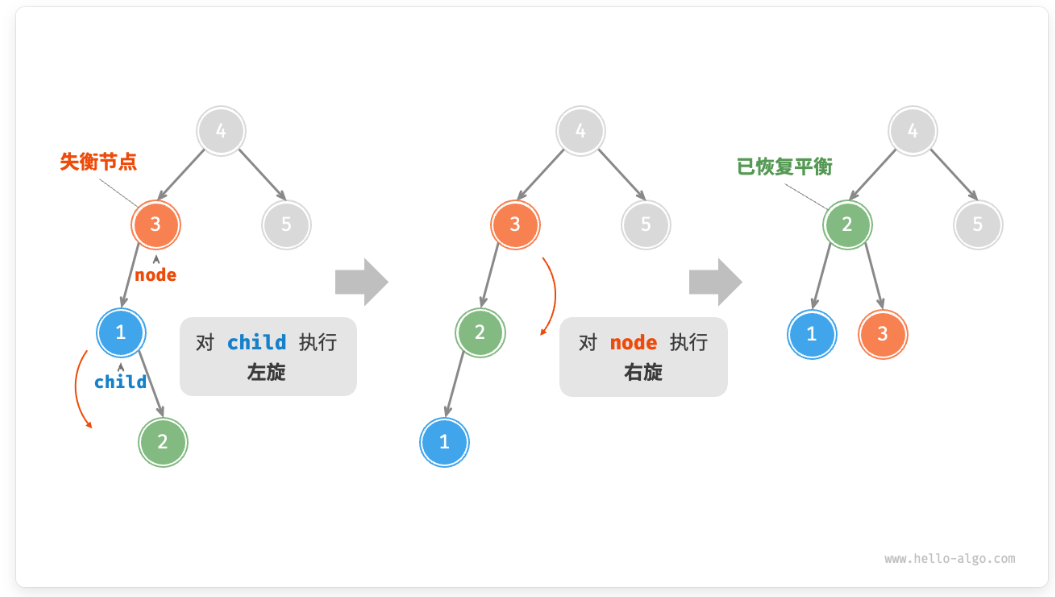
而这时，如果1节点是左右节点双全的（同理，如果左旋的右子节点是左右子节点双全），那么就正常右旋，将1的右节点给3节点当左节点。