当前位置：首页 > news >正文

《算法导论》第 33 章 - 计算几何学

news 2025/8/21 12:16:32

大家好！今天我们来深入讲解《算法导论》第 33 章 ——计算几何学。计算几何学是计算机科学的重要分支，核心是用算法解决几何问题，广泛应用于图形学、机器人导航、GIS（地理信息系统）、自动驾驶等领域。本章将从基础的线段性质入手，逐步讲解线段相交检测、凸包寻找、最近点对查找等经典问题，每个知识点都配套完整可编译的 C++ 代码、清晰的流程图和类图，方便大家动手实践。

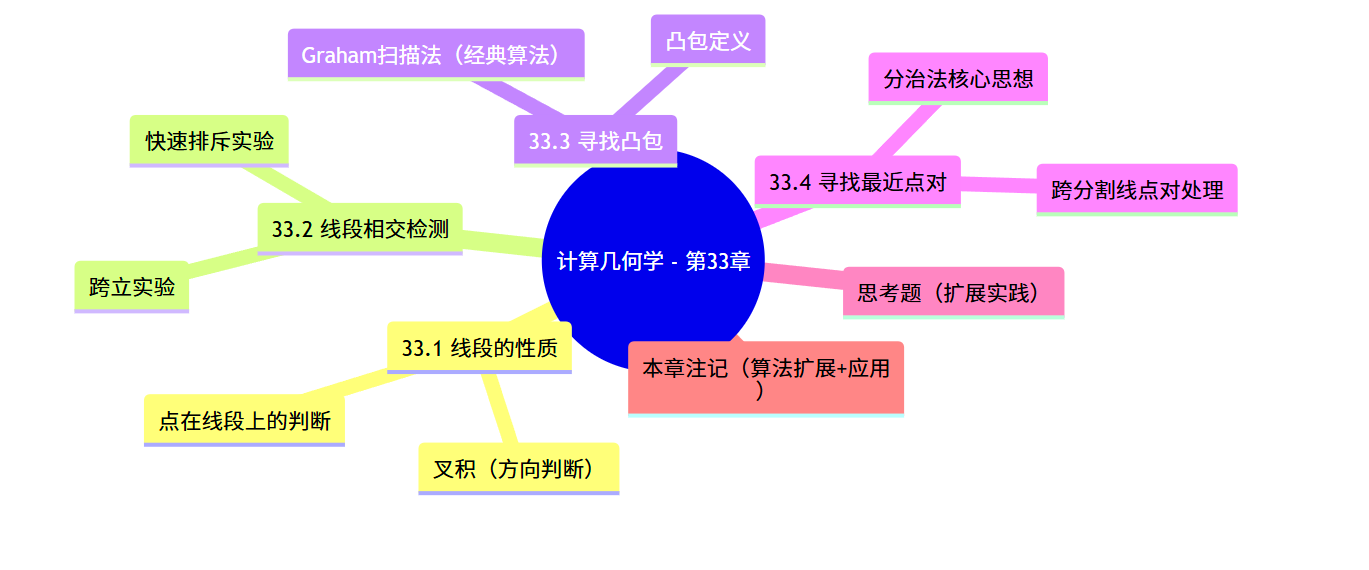
本章内容思维导图

33.1 线段的性质

线段是计算几何学的基础元素，本节重点讲解叉积（判断向量方向）和点在线段上的判断两个核心问题。

1.1 核心概念

（1）叉积：向量方向的 “指南针”

（2）点在线段上的判断

1.2 关键函数实现

首先定义全局精度常量（处理浮点数误差），再实现叉积和点在线段判断函数：

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <stack>
#include <utility>
using namespace std;// 浮点数精度控制（避免直接比较 == 导致的误差）
const double EPS = 1e-8;// 点类：存储x、y坐标，提供基础操作
class Point {
private:double x, y;
public:// 构造函数Point() : x(0.0), y(0.0) {}Point(double x_, double y_) : x(x_), y(y_) {}// 访问器double getX() const { return x; }double getY() const { return y; }// 修改器void setX(double x_) { x = x_; }void setY(double y_) { y = y_; }// 重载 < 运算符（用于按x排序，x相同按y排序）bool operator<(const Point& p) const {if (fabs(x - p.x) > EPS) {return x < p.x;} else {return y < p.y;}}
};// 1. 计算叉积 cross(p0p1, p0p2)
double cross(const Point& p0, const Point& p1, const Point& p2) {return (p1.getX() - p0.getX()) * (p2.getY() - p0.getY()) - (p1.getY() - p0.getY()) * (p2.getX() - p0.getX());
}// 2. 判断点p是否在线段s上（s由a和b组成）
bool onSegment(const Point& p, const Point& a, const Point& b) {// 条件1：p、a、b共线（叉积接近0）if (fabs(cross(a, b, p)) > EPS) {return false;}// 条件2：p的x和y在a、b的范围内（取min和max避免线段方向影响）bool xInRange = (p.getX() >= min(a.getX(), b.getX()) - EPS) && (p.getX() <= max(a.getX(), b.getX()) + EPS);bool yInRange = (p.getY() >= min(a.getY(), b.getY()) - EPS) && (p.getY() <= max(a.getY(), b.getY()) + EPS);return xInRange && yInRange;
}

1.3 综合案例：点在线段判断

需求：输入一个线段（两个端点）和一个点，判断该点是否在线段上。

// 测试点在线段上的功能
void testOnSegment() {cout << "=== 测试点在线段判断 ===" << endl;double x1, y1, x2, y2, px, py;cout << "请输入线段的两个端点（x1 y1 x2 y2）：";cin >> x1 >> y1 >> x2 >> y2;cout << "请输入待判断的点（x y）：";cin >> px >> py;Point a(x1, y1), b(x2, y2), p(px, py);if (onSegment(p, a, b)) {cout << "点(" << px << "," << py << ")在线段上！" << endl;} else {cout << "点(" << px << "," << py << ")不在线段上！" << endl;}
}

33.2 确定任意一对线段是否相交

判断两条线段是否相交是碰撞检测、图形裁剪的核心问题，需通过快速排斥实验和跨立实验两步验证。

2.1 核心原理

（1）快速排斥实验（初步筛选）

两条线段 (s1(p1,p2)) 和 (s2(p3,p4)) 的包围盒（轴对齐的最小矩形）若不重叠，则线段一定不相交。包围盒重叠的条件：

s1 的 x 范围与 s2 的 x 范围重叠；
s1 的 y 范围与 s2 的 y 范围重叠。

（2）跨立实验（精确判断）

若两条线段相交，则每条线段的两个端点必须 “跨立” 在另一条线段的两侧（或共线且在线段上）。用叉积判断跨立：

只有快速排斥实验通过 + 跨立实验通过，两条线段才相交。

2.2 数据结构：线段类

首先定义线段类（依赖 Point 类），并用 PlantUML 展示类结构：

@startuml
class Point {- double x- double y+ Point()+ Point(double x, double y)+ double getX() const+ double getY() const+ void setX(double x)+ void setY(double y)+ bool operator<(const Point& p) const
}class Segment {- Point a  // 线段起点- Point b  // 线段终点+ Segment()+ Segment(Point a, Point b)+ Point getA() const+ Point getB() const+ void setA(Point a)+ void setB(Point b)
}@enduml

线段类的 C++ 实现：

// 线段类：由两个点组成
class Segment {
private:Point a, b;
public:// 构造函数Segment() : a(Point()), b(Point()) {}Segment(const Point& a_, const Point& b_) : a(a_), b(b_) {}// 访问器Point getA() const { return a; }Point getB() const { return b; }// 修改器void setA(const Point& a_) { a = a_; }void setB(const Point& b_) { b = b_; }
};

2.3 关键函数实现：线段相交判断

// 判断两条线段s1和s2是否相交
bool segIntersect(const Segment& s1, const Segment& s2) {Point p1 = s1.getA(), p2 = s1.getB();Point p3 = s2.getA(), p4 = s2.getB();// 步骤1：快速排斥实验double x1_min = min(p1.getX(), p2.getX()), x1_max = max(p1.getX(), p2.getX());double x2_min = min(p3.getX(), p4.getX()), x2_max = max(p3.getX(), p4.getX());double y1_min = min(p1.getY(), p2.getY()), y1_max = max(p1.getY(), p2.getY());double y2_min = min(p3.getY(), p4.getY()), y2_max = max(p3.getY(), p4.getY());// 若包围盒不重叠，直接返回falseif (x1_max < x2_min - EPS || x2_max < x1_min - EPS ||y1_max < y2_min - EPS || y2_max < y1_min - EPS) {return false;}// 步骤2：跨立实验double c1 = cross(p1, p2, p3);  // p3相对于s1的转向double c2 = cross(p1, p2, p4);  // p4相对于s1的转向double c3 = cross(p3, p4, p1);  // p1相对于s2的转向double c4 = cross(p3, p4, p2);  // p2相对于s2的转向// 情况1：严格跨立（叉积符号相反）if ((c1 * c2 < -EPS) && (c3 * c4 < -EPS)) {return true;}// 情况2：其中一个点在线段上（共线且在范围内）if (fabs(c1) < EPS && onSegment(p3, p1, p2)) return true;if (fabs(c2) < EPS && onSegment(p4, p1, p2)) return true;if (fabs(c3) < EPS && onSegment(p1, p3, p4)) return true;if (fabs(c4) < EPS && onSegment(p2, p3, p4)) return true;// 其他情况：不相交return false;
}

2.4 综合案例：多线段相交检测

需求：输入多条线段，判断每一对线段是否相交，并输出结果。

// 测试多线段相交检测
void testSegIntersect() {cout << "=== 测试多线段相交检测 ===" << endl;int n;cout << "请输入线段的数量：";cin >> n;vector<Segment> segments(n);// 输入每条线段的两个端点for (int i = 0; i < n; i++) {double x1, y1, x2, y2;cout << "请输入第" << i+1 << "条线段的端点（x1 y1 x2 y2）：";cin >> x1 >> y1 >> x2 >> y2;segments[i] = Segment(Point(x1, y1), Point(x2, y2));}// 检查所有线段对（i < j，避免重复）cout << "\n相交的线段对：" << endl;bool hasIntersect = false;for (int i = 0; i < n; i++) {for (int j = i+1; j < n; j++) {if (segIntersect(segments[i], segments[j])) {cout << "第" << i+1 << "条线段与第" << j+1 << "条线段相交" << endl;hasIntersect = true;}}}if (!hasIntersect) {cout << "没有相交的线段对" << endl;}
}

33.3 寻找凸包

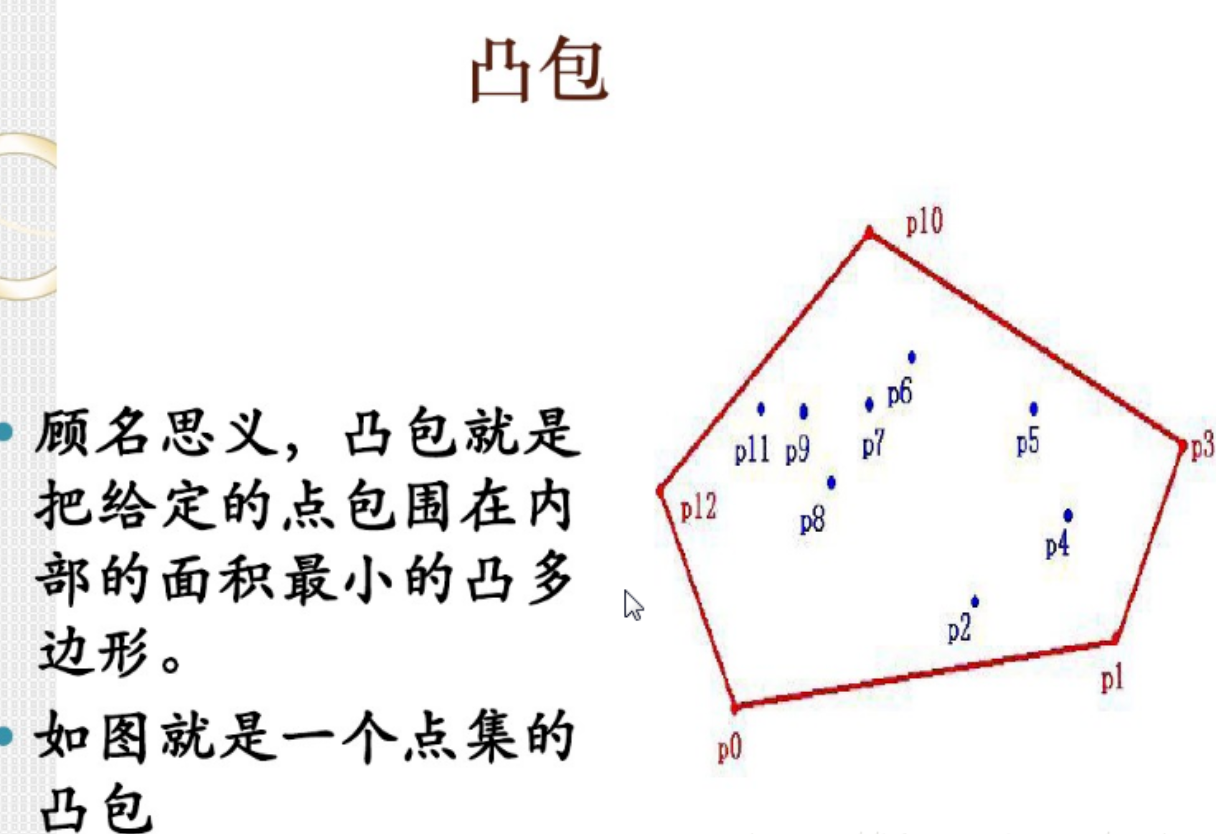
凸包是点集的 “最小凸多边形外壳”，包含点集中所有点，且多边形内任意两点的连线都在多边形内。本节讲解经典的Graham 扫描法。

3.1 核心概念

凸包顶点：凸包多边形的顶点（点集中 “最外围” 的点）；
极角：以某个基准点（如 y 最小的点）为原点，点与原点连线与 x 轴正方向的夹角（用于排序点）。

3.2 Graham 扫描法步骤

Graham 扫描法通过 “排序 + 栈维护” 寻找凸包，步骤如下：

找基准点：选择 y 坐标最小的点 (p_0)（y 相同选 x 最小的），确保它是凸包的一个顶点；
按极角排序：将其他点按与 (p_0) 的极角从小到大排序（极角相同则按距离 (p_0) 由近到远排序）；
栈维护凸包：
- 初始化栈，压入 (p_0, p_1, p_2)；
- 遍历剩余点 (p_i)，每次判断栈顶两个点与 (p_i) 的转向：
  - 若为非左转（叉积 ≤ 0），弹出栈顶点（该点不在凸包上）；
  - 若为左转，将 (p_i) 压入栈；
栈结果：最终栈中的点即为凸包顶点（按逆时针顺序排列）。

3.3 关键函数实现：Graham 扫描法

// 计算两点间的距离（平方，避免开方开销，比较时可用）
double distSq(const Point& a, const Point& b) {double dx = a.getX() - b.getX();double dy = a.getY() - b.getY();return dx*dx + dy*dy;
}// 计算两点间的实际距离
double dist(const Point& a, const Point& b) {return sqrt(distSq(a, b));
}// 极角排序的比较函数（以p0为基准）
bool comparePolar(const Point& p0, const Point& p1, const Point& p2) {double c = cross(p0, p1, p2);if (fabs(c) > EPS) {return c > 0;  // 左转：p1在p2前面（极角小）} else {// 共线：距离p0近的在前面（避免冗余点）return distSq(p0, p1) < distSq(p0, p2);}
}// Graham扫描法寻找凸包，返回凸包顶点（逆时针顺序）
vector<Point> grahamScan(vector<Point> points) {int n = points.size();if (n <= 1) return points;  // 点数≤1，凸包就是自身// 步骤1：找基准点p0（y最小，y相同x最小）int minIdx = 0;for (int i = 1; i < n; i++) {if (points[i].getY() < points[minIdx].getY() - EPS ||(fabs(points[i].getY() - points[minIdx].getY()) < EPS && points[i].getX() < points[minIdx].getX() - EPS)) {minIdx = i;}}swap(points[0], points[minIdx]);  // p0移到第一个位置Point p0 = points[0];// 步骤2：按极角排序（排除p0）sort(points.begin() + 1, points.end(), [&](const Point& p1, const Point& p2) {return comparePolar(p0, p1, p2);});// 步骤3：栈维护凸包stack<Point> st;st.push(points[0]);st.push(points[1]);for (int i = 2; i < n; i++) {// 弹出非左转的点（栈至少有2个点才判断）while (st.size() >= 2) {Point pTop1 = st.top(); st.pop();Point pTop2 = st.top();// 计算pTop2 -> pTop1 -> points[i]的转向if (cross(pTop2, pTop1, points[i]) <= EPS) {// 非左转，pTop1不在凸包上，继续弹出continue;} else {// 左转，将pTop1放回栈，退出循环st.push(pTop1);break;}}st.push(points[i]);}// 步骤4：将栈转为向量（凸包顶点）vector<Point> convexHull;while (!st.empty()) {convexHull.push_back(st.top());st.pop();}// 栈是逆序的，反转后得到逆时针顺序reverse(convexHull.begin(), convexHull.end());return convexHull;
}

3.4 综合案例：生成点集的凸包

需求：输入一组点，输出凸包的顶点（按逆时针顺序）和凸包的周长。

// 计算凸包的周长
double convexHullPerimeter(const vector<Point>& convexHull) {int m = convexHull.size();if (m <= 1) return 0.0;double perimeter = 0.0;for (int i = 0; i < m; i++) {int j = (i + 1) % m;  // 最后一个点连回第一个点perimeter += dist(convexHull[i], convexHull[j]);}return perimeter;
}// 测试Graham扫描法寻找凸包
void testGrahamScan() {cout << "=== 测试Graham扫描法寻找凸包 ===" << endl;int n;cout << "请输入点的数量：";cin >> n;vector<Point> points(n);// 输入每个点的坐标for (int i = 0; i < n; i++) {double x, y;cout << "请输入第" << i+1 << "个点的坐标（x y）：";cin >> x >> y;points[i] = Point(x, y);}// 计算凸包vector<Point> convexHull = grahamScan(points);int m = convexHull.size();// 输出结果cout << "\n凸包顶点（逆时针顺序）：" << endl;for (int i = 0; i < m; i++) {cout << "(" << convexHull[i].getX() << "," << convexHull[i].getY() << ") ";}cout << "\n凸包周长：" << convexHullPerimeter(convexHull) << endl;
}

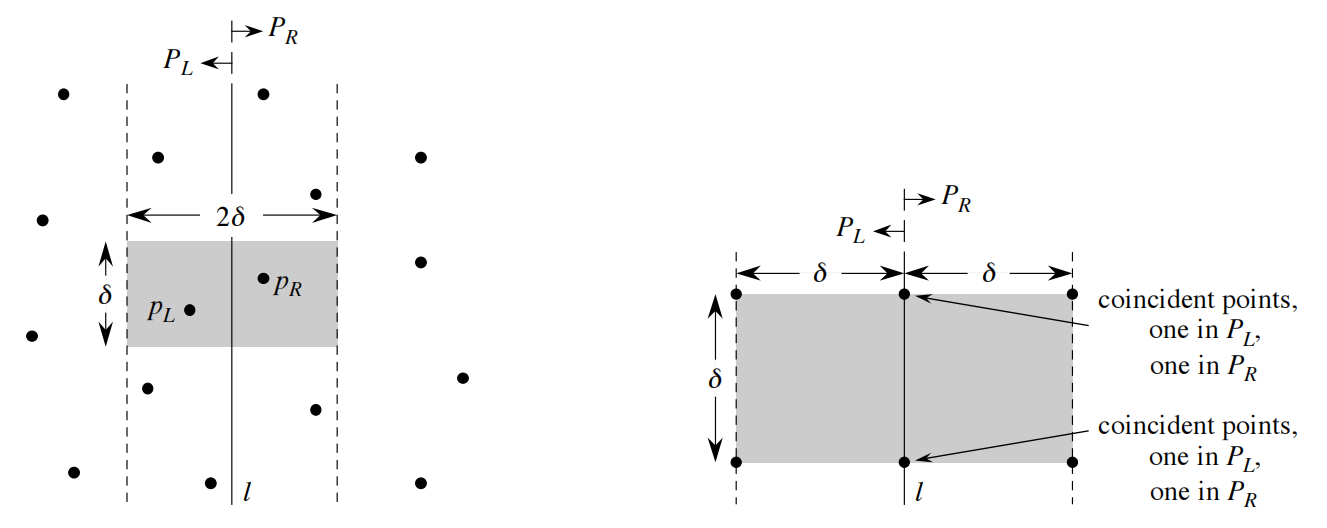
33.4 寻找最近点对

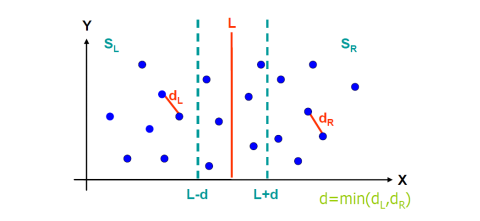
最近点对问题是：在平面点集中找到距离最小的一对点。本节用分治法解决，时间复杂度为 (O(n \log n))。

4.1 分治法核心思想

分治法的核心是 “分而治之”，将问题拆分为子问题，解决子问题后合并结果：

分割：将点集按 x 坐标排序后，分成左半部分 L 和右半部分 R（各含 (n/2) 个点）；
求解子问题：递归寻找 L 的最近点对（距离 d1）和 R 的最近点对（距离 d2），取 (d = min(d1, d2))；
合并：处理跨分割线的点对（即一个点在 L、一个点在 R）：
- 收集距离分割线（L 的最右点 x 坐标）≤ d 的点，组成集合 S；
- 将 S 按 y 坐标排序，对每个点 p，只需与后面6 个点比较（数学证明：(d×2d) 的矩形内最多有 6 个距离≥d 的点）；
- 找到 S 中的最小距离 d3，最终最近距离为 (min(d, d3))。

4.2 关键函数实现：分治法寻找最近点对

// 暴力法寻找最近点对（用于n ≤ 3的情况）
pair<Point, Point> bruteForce(const vector<Point>& points) {int n = points.size();pair<Point, Point> closestPair = {points[0], points[1]};double minDist = distSq(points[0], points[1]);// 遍历所有点对for (int i = 0; i < n; i++) {for (int j = i+1; j < n; j++) {double dSq = distSq(points[i], points[j]);if (dSq < minDist - EPS) {minDist = dSq;closestPair = {points[i], points[j]};}}}return closestPair;
}// 处理跨分割线的点集strip，寻找距离小于d的最近点对
pair<Point, Point> findClosestInStrip(vector<Point>& strip, double d) {int m = strip.size();pair<Point, Point> closestPair = {strip[0], strip[1]};double minDist = distSq(strip[0], strip[1]);// 按y坐标排序stripsort(strip.begin(), strip.end(), [](const Point& a, const Point& b) {if (fabs(a.getY() - b.getY()) > EPS) {return a.getY() < b.getY();} else {return a.getX() < b.getX();}});// 每个点只需与后面6个点比较for (int i = 0; i < m; i++) {for (int j = i+1; j < m && (strip[j].getY() - strip[i].getY()) < d + EPS; j++) {double dSq = distSq(strip[i], strip[j]);if (dSq < minDist - EPS) {minDist = dSq;closestPair = {strip[i], strip[j]};}}}return closestPair;
}// 分治法寻找最近点对（递归函数，输入按x排序的点集）
pair<Point, Point> closestPairRecursive(vector<Point>& pointsX) {int n = pointsX.size();//  base case：n ≤ 3，暴力求解if (n <= 3) {return bruteForce(pointsX);}// 步骤1：分割点集为左半L和右半Rint mid = n / 2;Point midPoint = pointsX[mid];vector<Point> Lx(pointsX.begin(), pointsX.begin() + mid);vector<Point> Rx(pointsX.begin() + mid, pointsX.end());// 步骤2：递归求解子问题pair<Point, Point> leftPair = closestPairRecursive(Lx);pair<Point, Point> rightPair = closestPairRecursive(Rx);// 步骤3：计算子问题的最小距离ddouble d1 = distSq(leftPair.first, leftPair.second);double d2 = distSq(rightPair.first, rightPair.second);double d = min(d1, d2);pair<Point, Point> closest = (d1 < d2) ? leftPair : rightPair;// 步骤4：收集跨分割线的点集strip（距离midPoint.x ≤ d）vector<Point> strip;for (const Point& p : pointsX) {if (fabs(p.getX() - midPoint.getX()) < d + EPS) {strip.push_back(p);}}// 步骤5：处理strip中的点对，更新最近点对if (strip.size() >= 2) {pair<Point, Point> stripPair = findClosestInStrip(strip, sqrt(d));double d3 = distSq(stripPair.first, stripPair.second);if (d3 < d - EPS) {closest = stripPair;}}return closest;
}// 寻找最近点对的入口函数（先按x排序点集）
pair<Point, Point> findClosestPair(vector<Point> points) {int n = points.size();if (n < 2) {throw invalid_argument("点集数量必须≥2！");}// 按x坐标排序（分治法的前提）sort(points.begin(), points.end());return closestPairRecursive(points);
}

4.3 综合案例：寻找点集中的最近点对

需求：输入一组点，输出最近点对的坐标和它们的距离。

// 测试寻找最近点对
void testClosestPair() {cout << "=== 测试寻找最近点对 ===" << endl;int n;cout << "请输入点的数量（≥2）：";cin >> n;vector<Point> points(n);// 输入每个点的坐标for (int i = 0; i < n; i++) {double x, y;cout << "请输入第" << i+1 << "个点的坐标（x y）：";cin >> x >> y;points[i] = Point(x, y);}// 寻找最近点对try {pair<Point, Point> closest = findClosestPair(points);Point p1 = closest.first;Point p2 = closest.second;double minDist = dist(p1, p2);// 输出结果cout << "\n最近点对：" << endl;cout << "点1：(" << p1.getX() << "," << p1.getY() << ")" << endl;cout << "点2：(" << p2.getX() << "," << p2.getY() << ")" << endl;cout << "最小距离：" << minDist << endl;} catch (const invalid_argument& e) {cout << "错误：" << e.what() << endl;}
}

思考题

本节提供 2 道扩展思考题，帮助大家深化对本章算法的理解：

思考题 1：处理凸包中的共线点

问题：Graham 扫描法默认保留共线的点，如何修改算法，使凸包只保留共线线段的端点（去除中间冗余点）？

思路：在极角排序时，对共线点只保留距离基准点 p0 最远的点（近点会被远点 “覆盖”，不在凸包上）。

代码片段（修改极角排序比较函数）：

bool comparePolarOptimized(const Point& p0, const Point& p1, const Point& p2) {double c = cross(p0, p1, p2);if (fabs(c) > EPS) {return c > 0;  // 左转优先} else {// 共线：距离远的在后面（排序后保留最后一个，即最远点）return distSq(p0, p1) > distSq(p0, p2);}
}// 排序后去重共线点
vector<Point> optimizeCollinearPoints(const vector<Point>& sortedPoints, const Point& p0) {vector<Point> optimized;optimized.push_back(p0);for (int i = 1; i < sortedPoints.size(); i++) {// 若当前点与前一个点不共线，加入优化后的集合if (fabs(cross(p0, optimized.back(), sortedPoints[i])) > EPS) {optimized.push_back(sortedPoints[i]);}}return optimized;
}

思考题 2：优化最近点对的排序开销

问题：分治法中每次递归都对 strip 集按 y 排序，如何优化以减少排序开销？

思路：提前对整个点集按 y 排序，递归时将 y 排序的子集传递给子问题，合并时直接从 y 排序集中筛选 strip 点（无需重新排序）。

代码片段（优化后的递归函数）：

pair<Point, Point> closestPairOptimized(vector<Point> pointsX, vector<Point> pointsY) {int n = pointsX.size();if (n <= 3) return bruteForce(pointsX);// 分割int mid = n / 2;Point midPoint = pointsX[mid];vector<Point> Lx(pointsX.begin(), pointsX.begin() + mid);vector<Point> Rx(pointsX.begin() + mid, pointsX.end());// 分割pointsY为Ly和Ry（按midPoint的x）vector<Point> Ly, Ry;for (const Point& p : pointsY) {if (p.getX() < midPoint.getX() + EPS) {Ly.push_back(p);} else {Ry.push_back(p);}}// 递归auto leftPair = closestPairOptimized(Lx, Ly);auto rightPair = closestPairOptimized(Rx, Ry);double d1 = distSq(leftPair.first, leftPair.second);double d2 = distSq(rightPair.first, rightPair.second);double d = min(d1, d2);auto closest = (d1 < d2) ? leftPair : rightPair;// 筛选strip集（从pointsY中直接取，已按y排序）vector<Point> strip;for (const Point& p : pointsY) {if (fabs(p.getX() - midPoint.getX()) < d + EPS) {strip.push_back(p);}}// 后续逻辑不变...return closest;
}

本章注记

1. 算法扩展

凸包算法：除了 Graham 扫描法，还有 Jarvis 步进法（礼物包装法，适合凸包顶点少的场景）、QuickHull 算法（平均效率高，类似快速排序）；
最近点对算法：随机化算法（通过随机打乱点集降低最坏情况概率）、线性时间算法（在特定条件下，如点集按 x/y 排序）。

2. 精度注意事项

计算几何学大量使用浮点数，必须注意精度误差：

避免直接用 == 比较浮点数，改用 fabs(a - b) < EPS 判断 “近似相等”；
EPS 的取值需根据场景调整（如毫米级精度用 1e-3，微米级用 1e-6）。

3. 实际应用场景

图形学：碰撞检测（线段相交）、纹理映射（凸包简化模型）；
机器人导航：路径规划（凸包简化障碍物）、避障（最近点对判断距离）；
GIS：区域最小包围矩形（基于凸包）、地图匹配（最近点对）；
自动驾驶：激光雷达点云处理（凸包提取障碍物轮廓）。

完整代码入口

将所有功能整合到主函数，通过菜单选择测试：

int main() {int choice;do {cout << "\n===== 《算法导论》第33章-计算几何学 =====" << endl;cout << "1. 测试点在线段判断" << endl;cout << "2. 测试多线段相交检测" << endl;cout << "3. 测试Graham扫描法寻找凸包" << endl;cout << "4. 测试寻找最近点对" << endl;cout << "0. 退出" << endl;cout << "请选择功能（0-4）：";cin >> choice;switch (choice) {case 1: testOnSegment(); break;case 2: testSegIntersect(); break;case 3: testGrahamScan(); break;case 4: testClosestPair(); break;case 0: cout << "退出程序！" << endl; break;default: cout << "无效选择，请重新输入！" << endl;}} while (choice != 0);return 0;
}