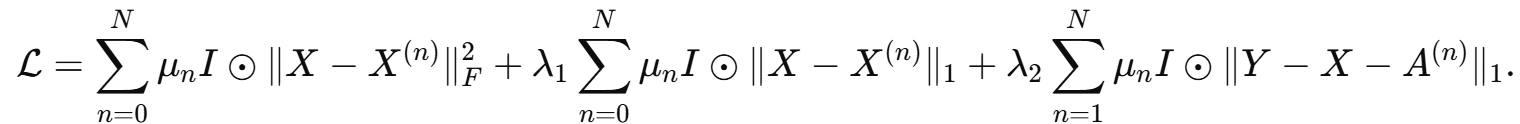当前位置：首页 > news >正文

【MAR】OSCNet+学习笔记

news 2025/8/21 10:22:27

1.基础知识理论

（1）CT成像系统

CT（计算机断层扫描）机器扫描得到的最初数据是投影数据（Projection Data）（也叫 弦图 / sinogram，其实就是X射线从不同角度穿过病人后测到的衰减值集合）。

1）投影数据产生过程

X射线发射：CT扫描过程中，X射线管发射一束X射线，这束X射线穿过人体的特定部位。
X射线衰减：当X射线穿过人体时，会与人体组织相互作用，导致X射线强度的衰减。不同密度和成分的组织（如骨骼、肌肉、脂肪等）对X射线的衰减程度不同。
探测器测量：穿过人体后的X射线被探测器接收，探测器测量到的是X射线的强度。这个强度反映了X射线在穿过人体过程中的衰减情况。

2）投影数据的形式

投影数据：探测器测量到的X射线强度数据被称为投影数据。这些数据是沿着X射线束的方向记录的，反映了X射线在穿过人体时的衰减情况。
投影角度：CT扫描过程中，X射线管和探测器会围绕人体旋转，通常旋转360度。在每个旋转角度上，探测器都会记录一组投影数据。这些投影数据从不同角度描述了人体内部结构的X射线衰减情况。

3)投影数据的数学表示

数学公式:

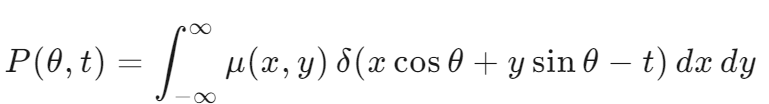
其中：

$P(\theta ,t)$ 是在角度 θ 和位置 t 处的投影数据。
$\mu (x,y)$ 是人体内部组织的线性衰减系数，表示X射线在位置 (x,y) 处的衰减程度。
$\delta$ 是狄拉克δ函数，用于表示X射线在特定路径上的衰减积分。

4)投影数据的处理

图像重建：投影数据是CT图像重建的原始数据。通过复杂的数学算法（如滤波反投影法、迭代重建法等），这些投影数据被转换成人体内部的二维或三维图像。
校正和预处理：在图像重建之前，投影数据通常需要进行一系列的校正和预处理操作，如暗场校正、增益校正、散射校正等，以提高图像质量和减少伪影。

（2）FBP（Filtered Back-Projection，滤波反投影法）

FBP算法主要分为两个步骤：滤波和反投影。

1）滤波（Filtering）
①目的：滤波的目的是补偿投影数据中的低频成分，增强高频成分，以减少图像中的模糊和伪影。
②过程：

傅里叶变换：将每个投影数据（sinogram的每一行）从空间域转换到频域。
应用滤波器：在频域中应用一个高通滤波器。常用的滤波器包括拉普拉斯滤波器、汉宁窗滤波器、汉明窗滤波器等。这些滤波器的作用是增强高频成分，减少低频成分。
逆傅里叶变换：将滤波后的频域数据逆变换回空间域，得到滤波后的投影数据。

③公式

对于每个投影角度 $\theta$ ，投影数据 $P(\theta ,t)$ 经过滤波后的数据 $P_{f}\left ( \theta ,t \right )$ 可以表示为：

其中：

$F$ 表示傅里叶变换。
$F^{-1}$ 表示逆傅里叶变换。
$\left | u \right |$ 是滤波器函数，通常是一个高通滤波器。

2）反投影（Back-Projection）
①目的：反投影的目的是将滤波后的投影数据投影回图像平面，重建出断层图像。
②过程：

逐像素累加：对于图像平面上的每个像素，根据每个投影方向上的滤波后投影数据，将相应的投影值累加到该像素上。具体来说，对于每个投影角度 θ 和每个探测器通道 t，将滤波后的投影值 P(θ,t) 投影到图像平面上，累加到对应的像素位置。
重建图像：通过上述累加过程，最终得到的图像就是重建后的断层图像。

③公式

重建后的图像 $f(x,y)$ 可以表示为：

其中：

$P_{f}\left ( \theta ,t \right )$ 是滤波后的投影数据。
$x\cos \theta +y\sin \theta$ 是投影数据在图像平面上的坐标。

（3）MAR传统方法

如果有金属，X射线几乎被完全吸收，导致对应位置的 投影数据缺失或失真。当这些不完整的投影数据被“反投影”成图像时，就会产生伪影。所以，传统方法的核心思路是：
👉 在图像重建之前，先把弦图中受金属影响的区域修复或替代。

① 线性插值（LI）

在投影域（sinogram）把金属对应的被污染 / 缺失的投影段“挖掉”，用邻近未被污染的数据做线性插值（沿探测器通道方向），然后用插值后的 sinogram 做常规重建（如 FBP）。

具体步骤

初步重建（可选）：对原始 sinogram 做一次快速重建（FBP），目的是得到一个能区分金属与软组织的图像（尽管伪影很多，但金属亮斑通常能被检测到）。
金属分割（图像域）：对重建图像做阈值分割得到金属二值掩码（例如 HU > 某个阈值）。常见阈值范围：2000–3000HU（与扫描器、重建窗口有关，需调参）。
前投影（forward project）：把图像域的金属掩码投影到投影域，得到 sinogram_mask(θ,s)（True/1 表示该 (角度θ, 探测器通道 s) 被金属影响）。可对掩码做膨胀（dilation）若干像素以覆盖金属边缘及周围散射效应。
按角度做插值：对每个投影角 θ，找到被 mask 覆盖的连续段，在探测器维度上用前后可用点做线性插值（也可以尝试二次 / 三次插值或样条）。
重建：用插值后的 sinogram 做 FBP（或其它反投影）得到最终图像。

为什么会有问题（LI 的缺陷）

插值值只从邻近通道借信息，不遵守 CT 的几何一致性（角度之间、不同探测器之间的全局关系），因此反投影后往往产生 二次伪影（新的条纹/模糊）。
对大尺寸金属或金属密集区域，周围未被污染的“可靠”数据太少，插值不稳定。

实现要点 / 调参建议

掩码膨胀：通常膨胀 2–10 像素（取决于 detector sampling）可减少边界效应。
端点处理：若掩码靠近探测器边缘，可能缺少两端端点，选择“最近值扩展”（nearest）或用外推。
插值方法：线性足够快；若 mask 小块且数据平滑可尝试 cubic/spline，但风险是过拟合振铃。
插值后平滑：对插值区做小尺度低通（gaussian）平滑，避免突然的投影不连续。

②归一化金属伪影还原（NMAR）

先构造一个**“先验”**（没有金属或金属被替换的参考图像），由此得到 先验的 sinogram，用先验对原始投影做归一化（把金属影响“标准化”成更易插值的形式），在归一化空间做插值，再把结果“去归一化”回真实投影域，从而减少插值带来的结构偏差。

为什么有用（直观）

直接在原始被污染投影上插值会被金属周围的高对比度“带偏”。用先验 sinogram 去除（或弱化）这种影响后，插值结果更“中性”、更接近真实组织投影，去归一化后更符合几何一致性。

详细流程

①初始 LI 修复
目的：通过快速插值方法对原始sinogram进行初步修复，得到一个初步的图像 $f_{LI}$ 。
步骤：

线性插值（LI）：在原始sinogram中，找到被金属污染或缺失的投影段，用邻近未被污染的数据进行线性插值。这种方法简单快速，但可能无法完全消除金属伪影。
重建初步图像：用插值后的sinogram进行常规重建（如FBP），得到初步图像 $f_{LI}$ .

②生成先验图像
目的：生成一个无金属或“金属被替换”的先验图像 $f_{prior}$ 。
步骤：

组织分割：对初步图像 $f_{LI}$ 进行组织分割，将图像中的组织分为不同的类别（如空气、软组织、骨骼等）。

金属区域替换：在初步图像中找到金属区域，并用周围软组织或骨组织的平均值替换金属区域。这样得到的图像 $f_{prior}$ 就是一个无金属或“金属被替换”的先验图像。

③前投影先验
目的：将先验图像 $f_{prior}$ 前投影，得到先验投影数据 $p_{prior}$ 或 $I_{prior}$ 。
步骤：

前投影：使用与CT扫描相同的几何参数，将先验图像 $f_{prior}$ 前投影，得到先验投影数据 $p_{prior}$ 或 $I_{prior}$ 。前投影过程是重建过程的逆过程，它将图像数据转换为投影数据。

④ 归一化
目的：对原始投影数据进行归一化处理，以减少金属伪影的影响。
步骤：
选择归一化方法：根据数据类型，选择合适的归一化方法。常见的归一化方法包括除法归一化和减法归一化。

先验与归一化的两种数学形式取决于你的 sinogram 存储的是哪种量：

情形 A：sinogram 存的是探测器原始强度/透射计数 $I(\theta ,s)$ （常见于原始数据）,归一化使用除法
情形 B：sinogram 存的line integrals $p(\theta ,s)$ （即通常的 sinogram）,归一化使用减法（因为 line integrals 可视为对数域.

务必确认你的 sinogram 是原始强度还是已经做了 -ln 变换（很多公开数据集直接提供的是 line integral）

除法归一化：将原始投影数据 $p$ 除以先验投影数据 $p_{prior}$ 。

减法归一化：将原始投影数据 $p$ 减去先验投影数据 $p_{prior}$ 。

⑤插值修复归一化后的投影
目的：对归一化后的投影数据进行插值修复，以进一步减少金属伪影的影响。
步骤：

插值方法：在归一化后的投影数据 $p_{norm}$ 中，找到被金属污染或缺失的投影段，用邻近未被污染的数据进行插值。常用的插值方法包括线性插值、样条插值等。

稳定性：在归一化域中进行插值通常比在原始域中进行插值更稳定，因为归一化后的数据更容易处理。

⑥ 去归一化
目的：将插值修复后的归一化投影数据恢复到原始数据的量纲。
步骤：
选择去归一化方法：根据归一化方法，选择相应的去归一化方法。

除法归一化的去归一化：将插值修复后的归一化投影数据 $p_{norm}$ 乘以先验投影数据 $p_{prior}$ 。

减法归一化的去归一化：将插值修复后的归一化投影数据 $p_{norm}$ 加上先验投影数据 $p_{prior}$ .

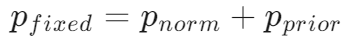
⑦重建
目的：用修复后的投影数据 $p_{fixed}$ 进行图像重建，得到最终的断层图像。
步骤：选择重建算法：可以选择常规的FBP算法或迭代重建算法。

FBP重建：使用FBP算法对修复后的投影数据 $p_{fixed}$ 进行重建，得到最终的断层图像。
迭代重建：使用迭代重建算法对修复后的投影数据 $p_{fixed}$ 进行重建，得到最终的断层图像。迭代重建算法通常可以提供更好的图像质量和更低的伪影水平，但计算复杂度较高。

总结

NMAR算法通过以下步骤减少CT图像中的金属伪影：

①初始LI修复：用线性插值对原始sinogram进行初步修复，得到初步图像 $f_{LI}$

②生成先验图像：对 $f_{LI}$ 进行组织分割，替换金属区域，得到先验图像 $f_{prior}$ 。

③前投影先验：将 $f_{prior}$ 前投影，得到先验投影数据 $p_{prior}$ 。

④归一化：对原始投影数据进行归一化处理。

⑤插值修复归一化后的投影：在归一化域中对投影数据进行插值修复。

⑥去归一化：将修复后的归一化投影数据恢复到原始数据的量纲。

⑦重建：用修复后的投影数据进行图像重建，得到最终的断层图像。

NMAR 的优点与局限

优点：比 LI 更能保留结构一致性，降低二次伪影。
局限：非常依赖 先验图像的质量（分割/金属替换不准确会把错误固定进去）。对于大面积数据丢失或金属数量很多的情况仍然不足。

实战细节与调参

先验图像生成：用 LI 重建后进行分割（阈值或基于形态学的连通性），再把金属像素替换为局部邻域（或整幅图）软组织/骨值的中值/均值。替换后可做小范围高斯平滑以避免锐边。
避免除零/低值：做除法时对 $p_{prior}$ 或 $I_{prior}$ 加上小常数 $\varepsilon$ （如 1e−61e-61e−6 或更大，取决单位）。
重复迭代：可以把 NMAR 做一次后再重复一次（用新重建生成更好先验）通常会进一步改善。
插值方法 & 平滑：同 LI。插值后做片段边界平滑，避免突然不连续。
评价：用 RMSE/SSIM 与 ground-truth（若有）比较；还要人工查看金属边缘处是否出现“假组织”边界。

2.摘要

问题背景：

CT（X光断层扫描）在临床上很常用。
但如果病人身体里有金属（比如牙科填充物、假体、钢钉等），就会在CT图像上出现伪影 —— 一些不真实的条纹或阴影，会干扰医生诊断。

现有方法的局限：

现在很多人用深度学习来去伪影，但这些方法通常只学到了“图像差异”，并没有充分利用伪影的物理特征。

他们的创新：

发现伪影的特点：金属伪影往往呈现出旋转对称的条纹（streaking patterns）。
设计了一个叫 OSCNet 的网络：
- 利用“方向共享卷积 (orientation-shared convolution)”来适应这些旋转对称的模式。
- 用傅里叶级数展开来建模伪影，帮助把伪影和真实组织分离。
- 采用“深度展开 (deep unfolding)”的思想：把一个优化算法（proximal gradient）转换成网络结构。
为了适应不同大小、不同类型金属造成的不同伪影，他们又在 OSCNet 里加了一个动态卷积子网络，形成 OSCNet+，提升了泛化能力。

结果：

他们在合成数据和临床数据上做了大量实验，证明 OSCNet/OSCNet+ 的效果优于现有方法。

3.用于编码金属伪影的方向共享卷积模型

（1）分解模型定义：

$I\bigodot X$ ：在非金属区域要恢复的“干净”CT 图像
$I\bigodot A$ ：在非金属区域的伪影
用逐点乘 ⊙ 和金属掩膜 I（I(i,j)=0 表示金属像素，=1 表示非金属像素）

只在非金属区域做恢复，金属区域本身不重建。

（2）先验观察：旋转对称条状（RSS, rotationally symmetrical streaking）

作者指出，金属伪影 A 在不同旋转角度上都呈现相似的条状结构。

⇒ 如果能用“同一组局部条状模式，在不同方向上旋转”来刻画 A，就能

显式地嵌入物理先验
显著减少可学习参数量（一组滤波器即可覆盖所有角度）

所以，提出用一组旋转共享的卷积滤波器来表示伪影 A，模型如下：

$L$ ：离散旋转角度的数量， $\theta _{l}=\frac{2\pi \left ( l-1 \right )}{L}$
每个方向上有 K 个“原子”/滤波器；。
$C_{k}\left ( \theta _{l} \right )\in \mathbb{R}^{p\times p}$ ：把同一个基础滤波器在角度 $\theta _{l}$ 上旋转之后的核（编码“条纹形态”）；
$M_{l,k}\in \mathbb{R}^{H\times W}$ :特征图，表示伪影在空间中的位置和强度。

解释

每个角度 $\theta _{l}$ 下，用 K 个滤波器 $C_{k}\left ( \theta _{l} \right )$ 来表示伪影的局部模式。
所有角度共享同一组“母滤波器” $C_{k}$ ，通过旋转矩阵 $T_{\theta _{l}}$ 生成不同角度的滤波器。
这种设计显著减少了需要学习的参数量，从 L×K 减少到 K。

这就显式地把“不同方向共享同一套模式”写进了模型：同一组基础滤波器在各个角度复用，只是位置系数不同。与普通“每个核只用于一个方向”的做法相比，它更贴合旋转对称条纹先验，且需要学习的核更少（参数更省、泛化更好）。

传统方法 = 每个方向学一套核；
OSCNet = 学一套基础核，通过旋转生成各方向的核，再配合不同的系数图表示伪影。

(3)傅里叶级数参数化——离散卷积核如何“可旋转”？

离散卷积核直接旋转会产生锯齿/走样。作者为此不直接学核的每个像素，而是先定义一个连续滤波器函数 $\varphi_k(\mathbf{x})$ ，用二维傅里叶级数基去表示，再通过坐标旋转来“旋转滤波器”。具体地，每个旋转后的核元素由

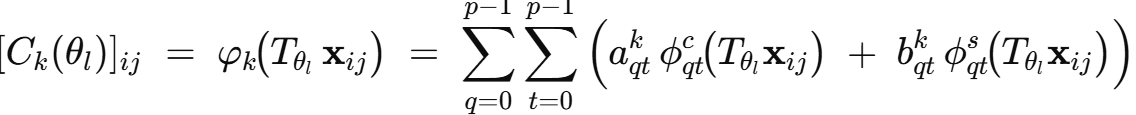
$\phi _{q,t}^{c}$ 与 $\phi _{q,t}^{s}$ ：带径向窗 $\Omega(\cdot)$ 的余弦/正弦基，作者把常规基频做了折返索引 $I_p(\cdot)$ 的修正，缓解旋转时的走样；
$T_{\theta _{l}}$ ：旋转矩阵，将坐标 $x_{ij}$ 旋转 $\theta _{l}$ ， $x_{ij}$ 是以核中心为原点的连续坐标；
可学习参数只有系数 $a_{q,t}^{(k)}$ , $b_{q,t}^{(k)}$ ：傅里叶系数，与角度无关，是全局可学习参数。并且在所有方向上共享（这就把“旋转对称”固化为“参数共享”）。训练时网络学的是这些系数；在任意角度 $\theta _{l}$ ，只需旋转坐标再取样即可生成 $C_{k}\left ( \theta _{l} \right )$ 。

与其“先学一堆离散核，再想办法旋转它们”，不如“先学一个可被旋转的连续滤波器（用傅里叶系数描述），需要哪个角度就把坐标旋转过去再采样”。这样旋转是“天然”的，同一套系数就能生成任意角度的核。

解释

通过傅里叶级数参数化，每个滤波器 $C_{k}\left ( \theta _{l} \right )$ 可以用一组傅里叶系数 $a_{q,t}^{(k)}$ 和 $b_{q,t}^{(k)}$ 表示。
旋转操作通过旋转矩阵 $T_{\theta _{l}}$ 实现，而傅里叶系数在所有角度下共享，从而实现“方向共享”。

（4）张量化紧凑表示

为了进一步简化模型，作者将上述模型写成张量形式：

$\Phi W$ ：用傅里叶基 $\Phi$ 和参数 $W$ 描述一个“连续可旋转的基础滤波器”；
$R\left ( \Phi W \right )$ ：对这个基础滤波器做旋转（可生成不同角度的版本）；
与 $M$ 卷积：把旋转后的核“铺在”图像不同位置上（系数图决定在哪里、强度多少）。

一个基础核（由 W 控制形状），旋转到不同角度后，再结合位置系数 M，就能生成整个伪影层 A。

4.OSCNet

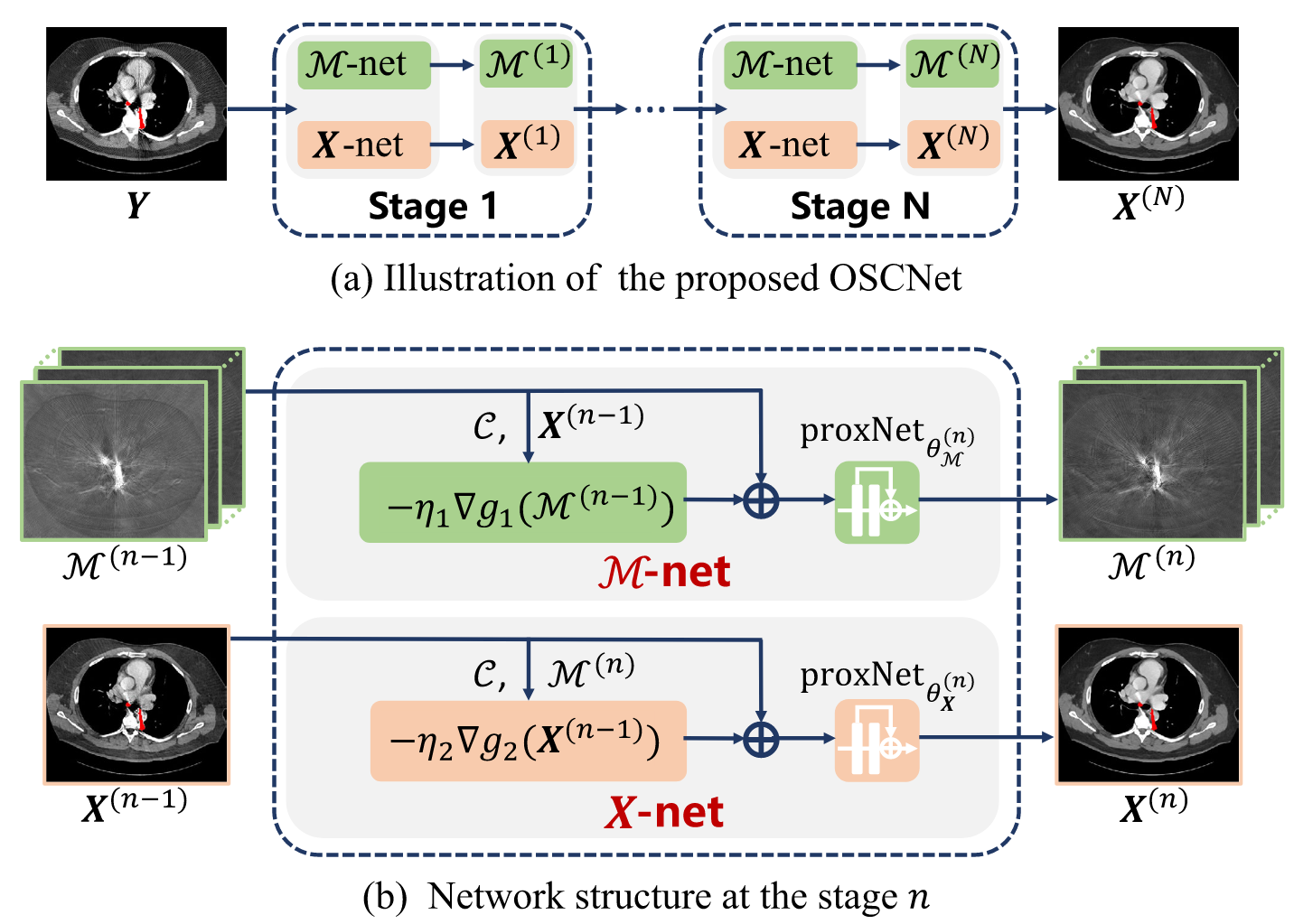
(1)核心目标

基于方向共享卷积模型，构建一个优化启发式的深度网络（OSCNet），用于 CT 图像的金属伪影去除。这个网络不仅显式地嵌入了金属伪影的旋转对称条状先验，还通过优化算法展开成网络结构，具有很强的可解释性和泛化能力。

(2)优化算法

在这一部分，作者首先提出了一个带正则化的优化问题，用于估计伪影层 A、特征图 M 和干净图像 X。优化问题如下：

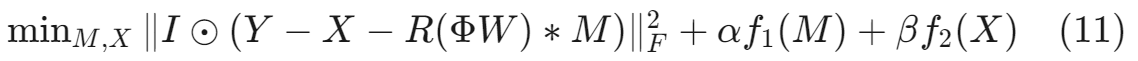
$\left \| \cdot \right \|_{F}$ ：Frobenius 范数，用于衡量重建误差。
$f_{1}\left ( M \right )$ 和 $f_{2}\left ( X \right )$ ：正则化项，分别对特征图 M 和干净图像 X 施加先验约束。
α 和 β：平衡参数，用于调整正则化项的权重。

为了求解这个优化问题，作者采用近端梯度算法，交替更新 M 和 X：

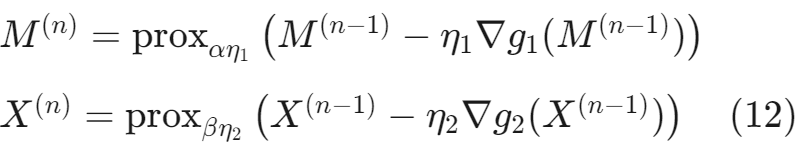
$\eta _{1}$ 和 $\eta _{2}$ ：步长参数。
$prox_{\alpha \eta _{1}}$ 和 $prox_{\beta \eta _{2}}$ ：近端算子，用于实现正则化项的约束。
$\triangledown g_{1}$ 和 $\triangledown g_{2}$ ：梯度计算。

(3)网络设计

基于上述优化算法，作者将每个迭代步骤展开成网络模块，构建了 OSCNet。具体网络结构如下：

①网络结构

M-net：用于更新特征图 M。
X-net：用于更新干净图像 X。
W-net：用于更新全局傅里叶系数 W（这部分在后续的 OSCNet+ 中进一步扩展）。

②网络模块

M-net 和 X-net：基于 ResNet 构建，每个模块包含多个残差块（ResBlock），每个残差块包含：

两个卷积层（Conv+BN+ReLU）。
一个跳跃连接（Skip Connection）。

W-net：用于动态更新傅里叶系数 W，包含多个卷积层、全局平均池化层、线性层和 ReLU 层。

③迭代过程

每个迭代阶段 n 包含 M-net 和 X-net 的更新。具体步骤如下：

1）计算梯度

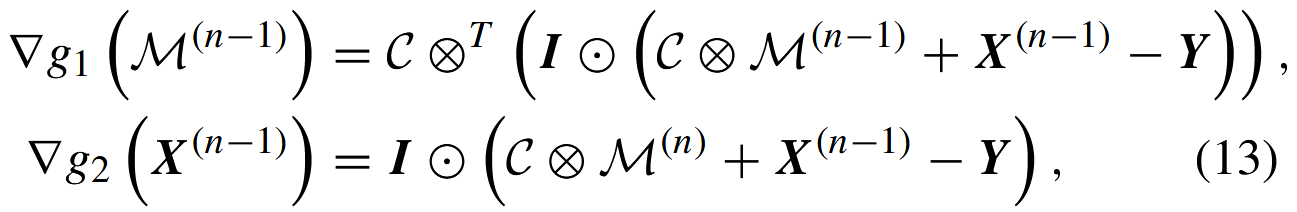
2）梯度下降

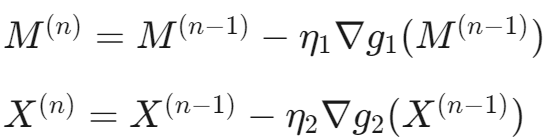
3）近端操作

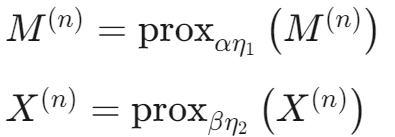
4）网络输出

经过 N 个迭代阶段后，网络输出最终的干净图像 X (N)。

5.动态 OSCNet

核心目标：提高 OSCNet 在处理不同大小和类型的金属伪影时的灵活性和泛化能力。通过动态调整卷积表示，使网络能够自适应地学习不同输入图像的伪影特征。

(1)优化算法

Dynamic OSCNet 的优化算法基于对原始优化问题的扩展，引入了动态调整的傅里叶系数矩阵 W。优化问题如下：

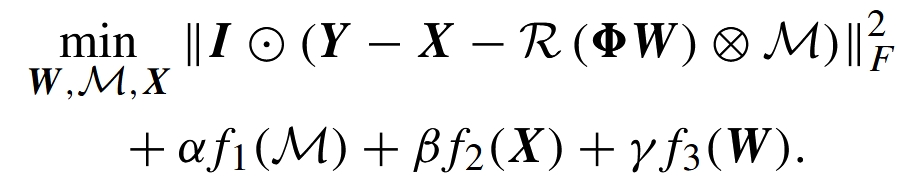
要点：与 OSCNet（W为全数据共享的可训练参数）不同，这里把 W 作为样本/阶段依赖的变量来处理 —— 于是需要一种方式在推理时根据输入动态生成 W。

用近端梯度思想对上个公式做迭代更新，作者推导得到在第 n 个阶段（迭代）下的更新式（核心三步）：

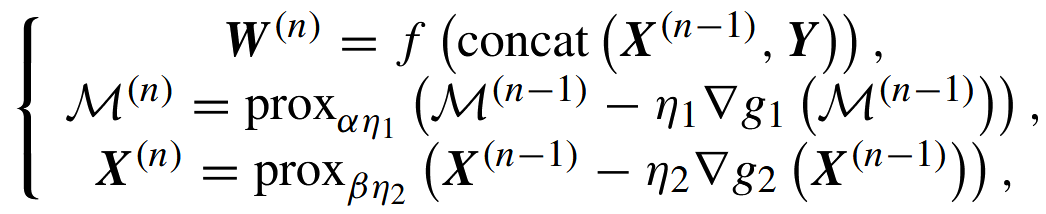
其中：

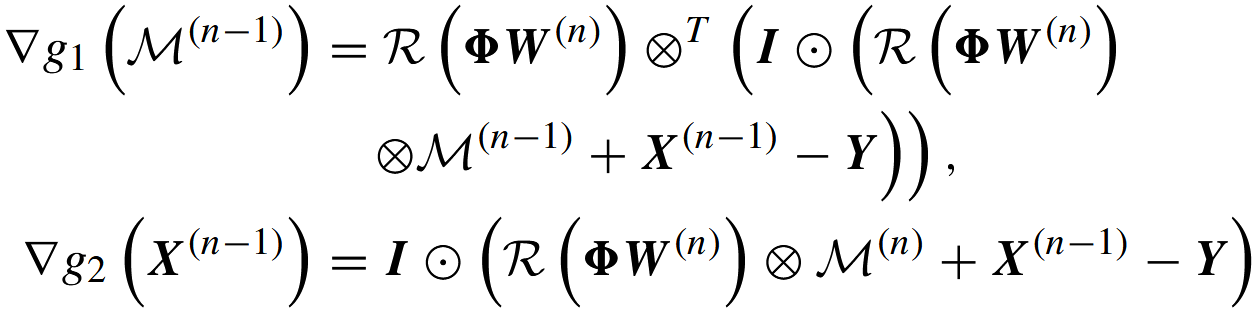
解释：

第一步 $W^{(n)}=f(\cdot)$ ：不再直接用梯度求解 W，而是用一个小的映射网络 f（后文叫做 W-net 或 WNet）把上一阶段重建 $X^{(n-1)}$ 和原始 Y 拼接作为输入，直接预测本阶段的 Fourier-扩展系数矩阵 $W^{(n)}$ 。这样 W 成为样本/阶段依赖的（动态）参数。
第二、三步：对 $\mathcal{M}$ 与 X做带近端项的梯度更新（proximal gradient），prox 操作通过网络模块实现（后文称 proxNet），以增加表达能力并引入非线性/先验。

直接把 W 交给一个小网络来输出，能把复杂的非线性依赖（伪影受金属大小、位置、组织差异影响）建模进去；而 M与 X 的更新仍保留“可解释”的优化式形式（proximal），便于将物理先验和网络表示结合。

(2)网络设计

作者把上面的迭代规则直接映射为可训练的网络模块（端到端学习所有参数）：在迭代阶段n， OSCNet+包括以下计算步骤：

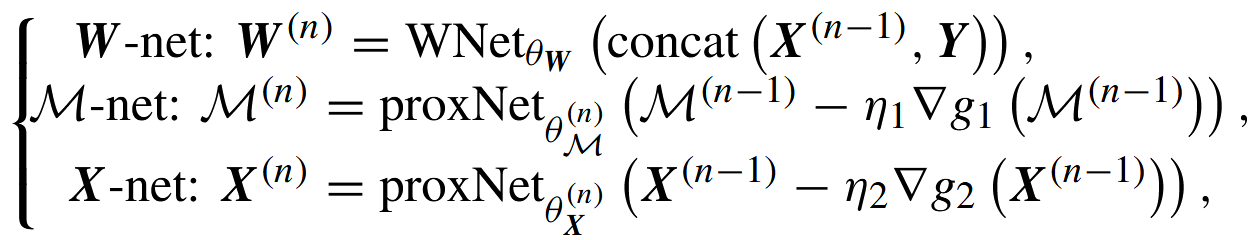
W-net（即映射 $f(\cdot)$ ）：

作者用 GAP + 全局信息 是关键：伪影“强弱”通常是全图级别（比如金属大则伪影强），全局统计信息能帮助 WNet 估计滤波器系数的能量分布；同时用少量卷积层保持轻量不会显著增加计算负担。WNet 实质上是个小巧的条件自适应生成器（类似 hyper-network）。

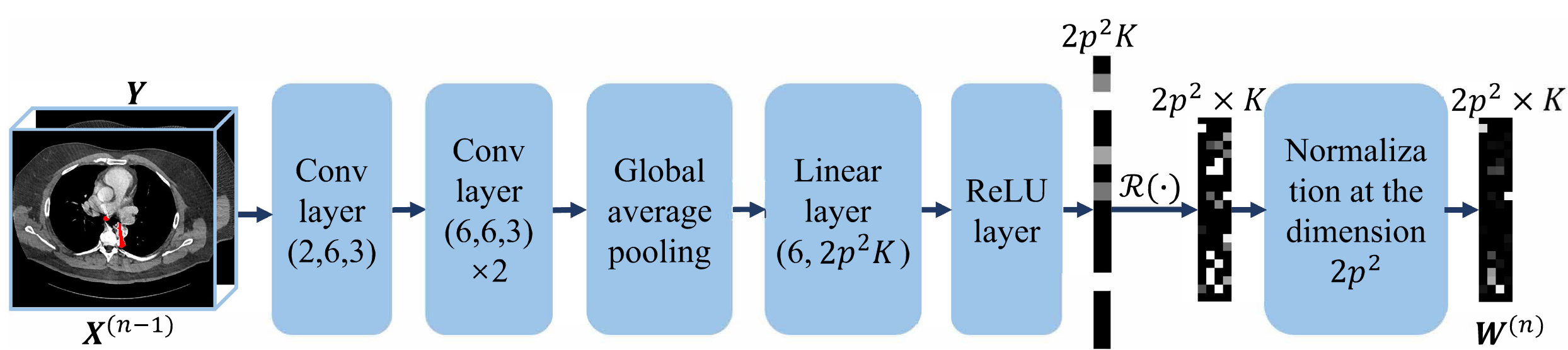
结构（论文/代码说明）：三层卷积用于提取局部特征 → 全局平均池化（GAP）获得全局强度信息 → ReLU（强制非负）→ reshape（把得到的向量映射为 Fourier-系数矩阵的形状）→ 归一化步骤（控制傅里叶展开系数能量，避免“放大”滤波器能量干扰提取）。
功能：把拼接的 $[X^{(n-1)},Y]$ 映射为这一阶段的展开系数 $W^{(n)}$ 。作者把 WNet 称作像“超网络（hyper-net）”—— 它根据每个样本和阶段输出不同的 W，从而实现动态滤波器生成。

M-net 与 X-net（proxNet）：

prox 操作由小的 ResNet 实现（每阶段不同参数）：每个 ResNet 由 T个残差块组成；每个残差块为 [Conv → BN → ReLU → Conv → BN + skip]。
这两个 proxNet 分别实现 p $\operatorname{prox}_{\alpha\eta_1}(\cdot)$ 和 $\operatorname{prox}_{\beta\eta_2}(\cdot)$ ，即学习型近端算子，负责把梯度步后的中间量投影/细化为更合理的 $M^{(n)}$ 与 $X^{(n)}$ 。在最末阶段作者还额外加了一个 ResNet 做最终细化。

R(ΦW) 的实现：

W 是傅里叶级数的展开系数，通过 $\Phi$ 与 $\mathcal{R}(\cdot)$ 得到空域滤波器（这一步是 OSC 的滤波器参数化细节——把 Fourier-系数映射回 p×p 空域卷积核）。作者使用这一参数化使滤波器易于旋转并共享方向先验（方向共享机制在 III 节有详细推导）。

训练目标（分阶段 supervision）：

作者对每个阶段的输出 $X^{(n)}$ 和伪影层 $A^{(n)}$ 采用逐阶段损失，整体 loss 的一个常见写法（论文给出）是 L2 + L1 混合、并对不同阶段加权：
所有网络参数（WNet 权重、各阶段 proxNet 的权值、步长参数 $\eta_1,\eta_2$ 、以及可能的正则参数）都是端到端训练的。