当前位置：首页 > news >正文

算法第五十二天：图论part03（第十一章）

news 2025/8/21 8:32:45

一.孤岛的总面积

101. 孤岛的总面积

🔹 核心思路

方向定义：
dir = [[0, 1], [1, 0], [-1, 0], [0, -1]]

表示上下左右四个方向，用于 DFS 遍历岛屿相邻的陆地。

DFS 函数：
def dfs(grid, x, y): global count grid[x][y] = 0 # 标记已经访问过，避免重复计数 count += 1 # 当前岛屿面积加 1 for i, j in dir: nextx = x + i nexty = y + j if nextx < 0 or nextx >= len(grid) or nexty < 0 or nexty >= len(grid[0]): continue if grid[nextx][nexty] == 1: dfs(grid, nextx, nexty)

功能：递归遍历当前岛屿的所有陆地单元格，并累计面积。

技巧：把访问过的陆地标记为 0，防止重复计算。

消除边界岛屿：
for i in range(n): if grid[i][0] == 1: dfs(grid, i, 0) if grid[i][m-1] ==1: dfs(grid, i, m-1) for j in range(m): if grid[0][j] == 1: dfs(grid, 0, j) if grid[n-1][j] == 1: dfs(grid, n-1, j)

目的：消除所有和边界相连的岛屿，因为它们不算作孤岛。

统计内部孤岛：
count = 0 # 重置计数器 for i in range(n): for j in range(m): if grid[i][j] == 1: dfs(grid, i, j) print(count)

遍历剩下的矩阵，如果遇到陆地 1，说明是孤岛的一部分，调用 DFS 并累计面积。

最终 count 就是所有孤岛的总面积。

🔹 总结流程

遍历矩阵的边界，将能连到边界的陆地消除。

遍历剩下的矩阵，对每块孤岛进行 DFS，累计面积。

输出

所有孤岛的总面积。

dir = [[0, 1], [1, 0], [-1, 0], [0, -1]]
count = 0def dfs(grid, x, y):global countgrid[x][y] = 0 # 标记已经访问过，避免重复计数count += 1for i, j in dir:nextx = x + inexty = y + jif nextx < 0 or nextx >= len(grid) or nexty < 0 or nexty >= len(grid[0]):continueif grid[nextx][nexty] == 1:dfs(grid, nextx, nexty)n, m = map(int, input().split())
grid = []
for i in range(n):grid.append(list(map(int, input().split())))
res = 0
#消除边界岛屿
for i in range(n):if grid[i][0] == 1:dfs(grid, i, 0)if grid[i][m-1] ==1:dfs(grid, i, m-1)
for j in range(m):if grid[0][j] == 1:dfs(grid, 0, j)if grid[n-1][j] == 1:dfs(grid, n-1, j)count = 0 #重新将count 置为0
for i in range(n):for j in range(m):if grid[i][j] == 1:dfs(grid, i, j)
print(count)

二.沉没孤岛

102. 沉没孤岛

💡 思路总结（沉没孤岛）

遍历边界 → DFS 标记
从矩阵的四条边出发，把所有与边界相连的陆地 1 用 DFS 改为 2，避免它们被误判为孤岛。

沉没孤岛
此时矩阵内部的 1 就是孤岛。遍历矩阵，把所有剩余的 1 直接改为 0，表示孤岛被沉没。

恢复边界岛屿
将之前标记过的 2 重新变回 1，表示边界岛屿仍然存在。

🔑 代码要点
dfs() 用于把边界连通的 1 标记为 2。

三轮遍历：

第一轮：边界 DFS 标记为 2。

第二轮：消灭孤岛（把 1 变 0）。

第三轮：把 2 恢复为 1。
输出时必须用
print(' '.join(map(str, row)))

否则会把 list 直接打印出来。


#思路：深搜或广搜把周边的1变成2 // 再利用dfs把孤岛变为0 // 然后再把2变为1
dir = [[0, 1], [1, 0], [-1, 0], [0, -1]]def dfs(grid, x, y):grid[x][y] = 2 # 标记已经访问过，避免重复计数for i, j in dir:nextx = x + inexty = y + jif nextx < 0 or nextx >= len(grid) or nexty < 0 or nexty >= len(grid[0]):continueif grid[nextx][nexty] == 1:dfs(grid, nextx, nexty)n, m = map(int, input().split())
grid = []
for i in range(n):grid.append(list(map(int, input().split())))#消除边界岛屿
for i in range(n):if grid[i][0] == 1:dfs(grid, i, 0)if grid[i][m-1] ==1:dfs(grid, i, m-1)
for j in range(m):if grid[0][j] == 1:dfs(grid, 0, j)if grid[n-1][j] == 1:dfs(grid, n-1, j)for i in range(n):for j in range(m):if grid[i][j] == 1:grid[i][j] = 0for i in range(n):for j in range(m):if grid[i][j] == 2:grid[i][j] = 1for row in grid:print(' '.join(map(str, row)))   #必须这么写 否则会把 list 直接打印出来

三.水流问题

103. 水流问题

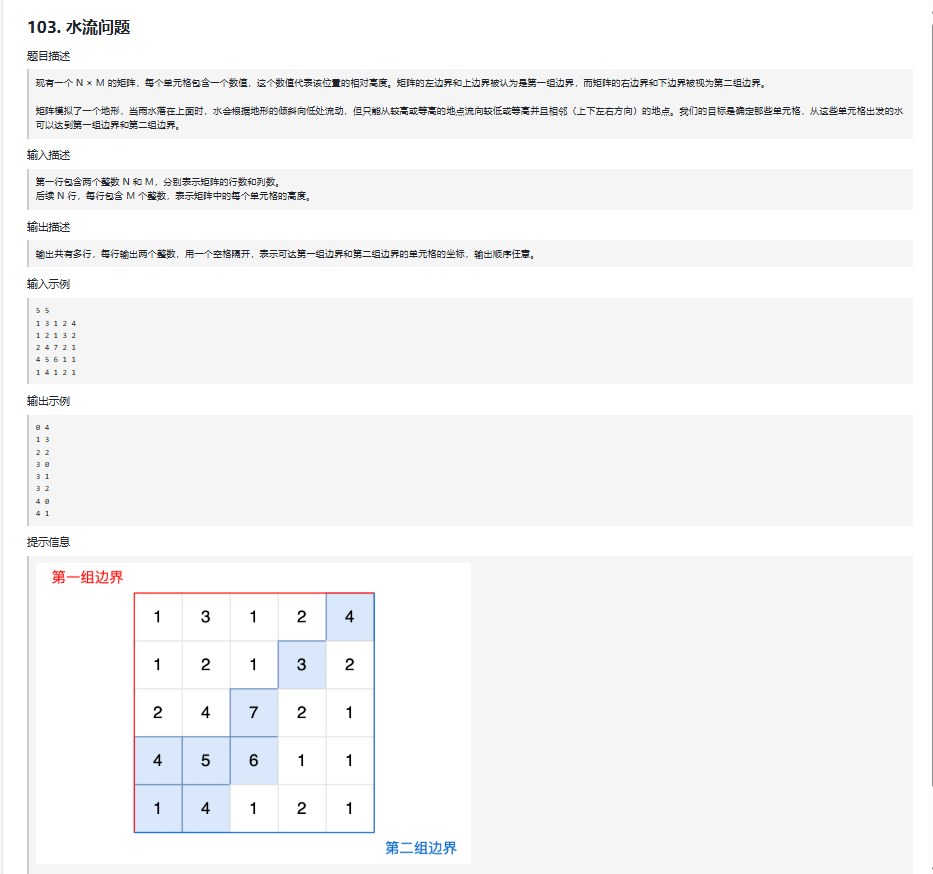
正确思路总结
边界 DFS 逆向思路

题目要求高往低流的点，同时能到两组边界。

解决方案是 从边界出发，逆向 DFS（从低到高）标记能到达边界的点。

分别对第一边界和第二边界做 DFS，记录可达点集合。
记录集合
用 set 记录可达边界的点坐标：
first = set() # 可到达第一边界 second = set() # 可到达第二边界
DFS 遇到新点就加入集合。
求交集
同时能到两组边界的点，就是两个集合的交集：
result = first & second
输出
按行列顺序排序输出，保证与题目期望一致：
for x, y in sorted(result): print(f"{x} {y}")
✅ 总结公式化思路：

从第一边界 DFS → 标记所有可到达第一边界的点 → first

从第二边界 DFS → 标记所有可到达第二边界的点 → second

交集 first & second → 输出

注意：

DFS 比较条件是“低往高”，模拟逆流。

visited 在一轮边界 DFS 中公用。

输出时要排序，避免集合无序造成顺序不同。

#条件：高往低流， 坐标需要满足可达第一组边界和第二组边界
direction = [[0, 1], [1, 0], [-1, 0], [0, -1]]
first = set()
second = set()def dfs(grid, visited, x, y, side):if visited[x][y]:returnvisited[x][y] = Trueside.add((x, y))for i, j in direction:nextx = x + inexty = y + j#从边界点反向流if 0 <= nextx < len(grid) and 0 <= nexty < len(grid[0]) and int(grid[x][y]) <= int(grid[nextx][nexty]):dfs(grid, visited, nextx, nexty, side)def main():global firstglobal second#输入n, m = map(int, input().strip().split())grid = []for i in range(n):row = input().strip().split()grid.append(row)#从第一边界开始visited = [[False] * m for _ in range(n)]for i in range(n):dfs(grid, visited, i, 0, first)for j in range(m):dfs(grid, visited, 0, j, first)#从第二边界开始visited = [[False] * m for _ in range(n)]for i in range(n):dfs(grid, visited, i, m-1, second)for j in range(m):dfs(grid, visited, n-1, j, second)result = first & secondfor x, y in sorted(result):print(f"{x} {y}")if __name__ == "__main__":main()

四.建造最大岛屿

104. 建造最大岛屿

解题思路

标记岛屿

遍历矩阵每个格子。

对每个陆地格子执行 DFS，将连通的岛屿标记为唯一的 mark。

DFS 返回岛屿的面积，记录在字典 rec[mark] 中。

翻水尝试

遍历每个水格子：

查看其上下左右相邻的岛屿有哪些（用集合避免重复）。

翻水后的岛屿面积 = 1 + 相邻岛屿面积和。

记录所有水格翻水后的最大面积。

返回结果

如果全是陆地，直接返回最大岛屿面积。

否则返回翻水后的最大岛屿面积。

算法关键点
DFS 返回值累加：
area = 1 for dx, dy in dir: nx, ny = x + dx, y + dy if 0 <= nx < n and 0 <= ny < m: area += dfs(grid, nx, ny, mark) return area

每个 DFS 返回子岛屿面积，递归累加。

不依赖外部变量或全局 count。
标记岛屿：

每个岛屿用唯一 mark 标记，避免重复计数。

翻水连接岛屿：

使用集合记录相邻岛屿，避免重复加面积。

边界处理：

DFS 中检查 (0 <= nx < n and 0 <= ny < m)。

翻水时同样检查边界。
时间复杂度分析

#最多可以将矩阵中的一格水变为一块陆地， 求矩阵中最大的岛屿面积是多少import collections
dir = [[0, 1], [1, 0], [-1, 0], [0, -1]]
def dfs(grid, x, y, mark):if grid[x][y] != 1:return 0#标记grid[x][y] = markarea = 1for i, j in dir:nextx = x + inexty = y + jif 0 <= nextx < len(grid) and 0 <= nexty < len(grid[0]):area += dfs(grid, nextx, nexty, mark)return areadef main():n, m = map(int, input().split())grid = []for i in range(n):row = list(map(int, input().strip().split()))grid.append(row)mark = 2rec = collections.defaultdict(int)#标记岛屿for i in range(n):for j in range(m):if grid[i][j] == 1:area = dfs(grid, i, j, mark)rec[mark] = area #记录岛屿的面积mark += 1#把水边为陆地result = max(rec.values(), default=0)  # 全是水的情况for i in range(n):for j in range(m):if grid[i][j] == 0:scount = 1v = set()for x, y in dir:newx = i + xnewy = j + yif 0 <= newx < len(grid) and 0 <= newy < len(grid[0]) and grid[newx][newy] != 0 and grid[newx][newy] not in v:scount += rec[grid[newx][newy]]v.add(grid[newx][newy])result = max(result, scount)print(result)if __name__ == "__main__":main()

今天的真的好难，最后一道题给我恶心到了！再见！加油

查看全文

http://www.dtcms.com/a/340846.html