曲面的交线的切向量计算及其在坐标平面投影的几何分析
在微分几何中,研究两个曲面相交形成的空间曲线性质具有重要理论和应用价值。本文将深入探讨两曲面 $ F_1(x,y,z) = 0 $ 与 $ F_5(x,y,z) = 0 $ 相交曲线的切向量计算及其在坐标平面投影的几何分析,并提供完整的 Python 实现。
数学原理
两曲面交线的切向量方向由曲面法向量的叉积给出:
T=∇F1×∇F5=∣ijk∂F1∂x∂F1∂y∂F1∂z∂F5∂x∂F5∂y∂F5∂z∣ \mathbf{T} = \nabla F_1 \times \nabla F_5 = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial F_1}{\partial x} & \frac{\partial F_1}{\partial y} & \frac{\partial F_1}{\partial z} \\ \frac{\partial F_5}{\partial x} & \frac{\partial F_5}{\partial y} & \frac{\partial F_5}{\partial z} \end{vmatrix} T=∇F1×∇F5= i∂x∂F1∂x∂F5j∂y∂F1∂y∂F5k∂z∂F1∂z∂F5
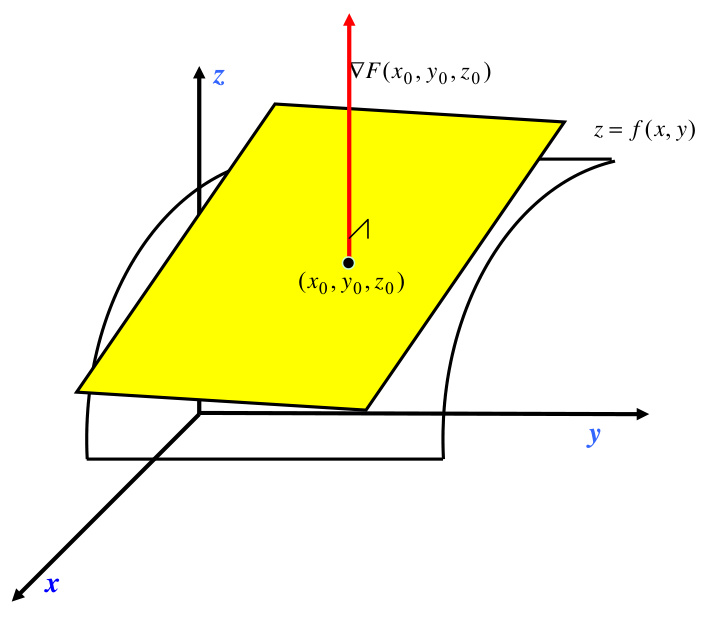
其中梯度 ∇F=(∂F∂x,∂F∂y,∂F∂z)\nabla F = \left( \frac{\partial F}{\partial x}, \frac{\partial F}{\partial y}, \frac{\partial F}{\partial z} \right)∇F=(∂x∂F,∂y∂F,∂z∂F) 表示曲面的法向量场。
该切向量 T=(Tx,Ty,Tz)\mathbf{T} = (T_x, T_y, T_z)T=(Tx,Ty,Tz) 的分量为:
{ Tx=∂F1∂y∂F5∂z−∂F1∂z∂F5∂yTy=∂F1∂z∂F5∂x−∂F1∂x∂F5∂zTz=∂F1∂x∂F5∂y−∂F1∂y∂F5∂x \begin{cases} T_x = \frac{\partial F_1}{\partial y} \frac{\partial F_5}{\partial z} - \frac{\partial F_1}{\partial z} \frac{\partial F_5}{\partial y} \\ T_y = \frac{\partial F_1}{\partial z} \frac{\partial F_5}{\partial x} -
