代码随想录刷题Day37

完全二叉树的节点个数

这道题如果使用层序遍历的方法，也是可以求出节点数目的，但是那样就没有用上完全二叉树的性质，这个性质会有所浪费。那该如何应用上呢？我自己尝试思考，还是没能想出来，最后还是看了代码随想录的解题思路。

完全二叉树看成是由满二叉树组成的（如下1树可以由2满二叉树 + 6满二叉树 +14满二叉树作为递归终点），这样做，可以节省一些，像层序遍历那样，挨个节点数的过程。因为满二叉树的节点数目可以直接根据层高来确定（如下2满二叉树，3层，节点数为2^3-1 = 7），而是否是满二叉树可以通过找最左节点和最右节点是否在同一层来判断：

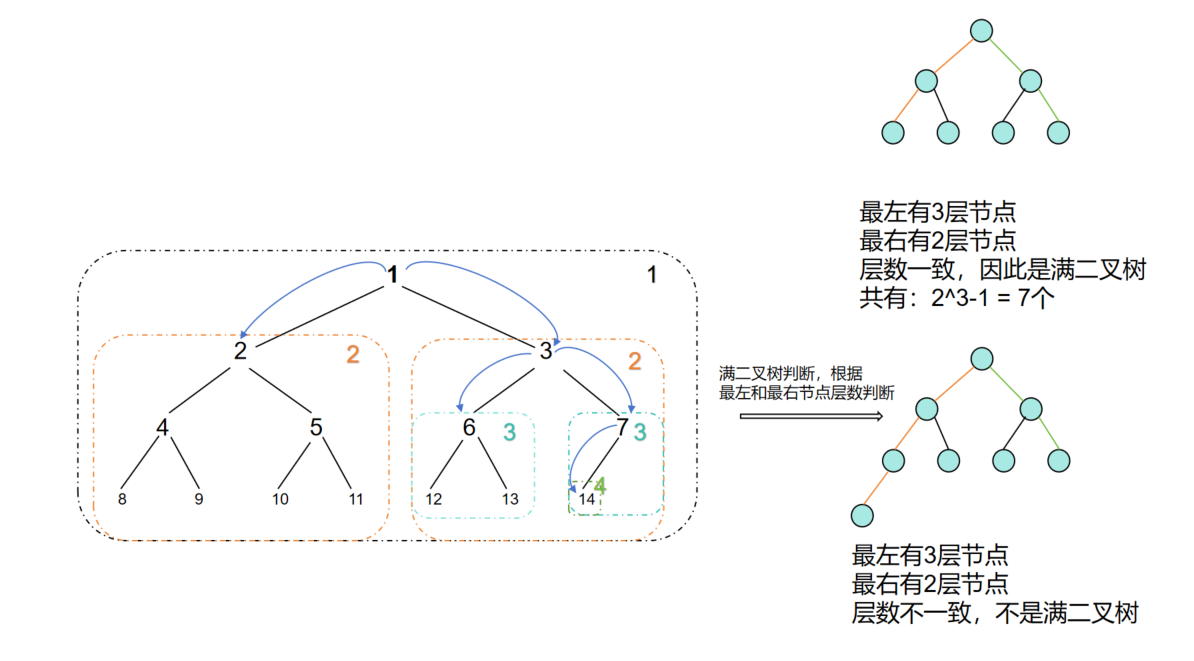
代码如下：

class Solution {
public:int countNodes(TreeNode* root) {//使用递归的方法计算完全二叉树的节点数目,也就是根据层高来计算节点数目//返回的值是满二叉树情况下的值if(root ==nullptr) return 0;int left_height = 0;int right_height = 0;int right_num = 0;TreeNode* left_left = root;TreeNode* right_right = root;//最左指针，和最右指针是否在同一层，是，则是满二叉树while(left_left){left_height ++;left_left = left_left ->left;}while(right_right){right_height++;right_num = right_num *2 +1;right_right = right_right->right;}if(left_height == right_height){//满二叉树，直接返回结果return right_num;}else{//否则就对左孩子和右孩子递归调用，加上根节点的数目return countNodes(root->left)+countNodes(root->right)+1;}}
};

平衡二叉树

这道题，根据平衡二叉树的定义展开代码的撰写：左右子树的深度不超过2，所以需要一个求树的深度的函数，而平衡二叉树的判断函数里，先判断当前节点是否满足左右子树地深度差距不超过2，如果满足，再递归检查左右子树是否满足，如果不满足则返回false：

class Solution {
public:int getHeight(TreeNode* root){//求树的深度if(root ==nullptr) return 0;else return max(getHeight(root->left),getHeight(root->right))+1;}bool isBalanced(TreeNode* root) {//左右子树的深度相差不超过2if(root==nullptr) return true;int left_height = getHeight(root->left);int right_height = getHeight(root->right);if(abs(left_height -right_height)<2){//需要递归地检查孩子节点是否也是平衡return isBalanced(root->left) && isBalanced(root->right);}else return false;}
};