C++的二叉搜索树(二叉排序树)

二叉搜索树

二叉搜索树的概念

二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值

若它的右子树不为空，则右子树上所有节点的值都大于根节点的值

它的左右子树也分别为二叉搜索树

eg.

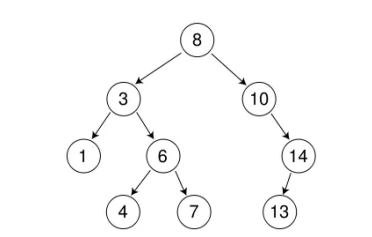
搜索二叉树的中序遍历是有序的

二叉搜索树可以用来进行查找,排序,去重

由于二叉搜索树本身节点的性质,默认情况下的二叉搜索树不允许进行节点的值的修改

二叉搜索树的插入

二叉搜索树由于本身的性质,可以用于排序或搜索

当二叉搜索树进行搜索时,可以不再进行暴力搜索,而是根据节点大小进行搜索,最多进行树的高度次即可成功搜索

由于二叉搜索树本身未必是完全二叉树,可能存在极端情况,因此他的增删查改的时间复杂度最坏情况为O(N)

但是,由于其本身的性质,一般的二叉搜索树是不允许节点冗余的,即不允许同一棵树存在相同大小的节点

	bool Insert(const K& key) // 插入节点{if (_root == nullptr) // 处理空树{_root = new Node(key);return true;}Node* parent = nullptr; // 父亲节点,用于存储当前节点的父节点Node* cur = _root;while (cur) // 寻找适合的位置{if (cur->_key < key){parent = cur; // 每次当前节点向下走时,存储当前节点为父节点cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else // 如果存在相同大小的节点就返回false,插入失败{return false;}}//通过与父节点比较大小,将节点插入适当位置cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}

 二叉搜索树的删除

二叉搜索树的删除分为多种情况

1.没有子节点的节点

直接删除该节点,并修改父节点的对应指针

2.只有一个子节点的节点

删除该节点后让其子节点代替该节点的位置

前两种情况可以总结为一种代码

eg:一个没有子节点的节点的左子树一定为空,若让他指向右子树,右子树也为空,则效果和直接指向空一致,而第二种情况,则可以直接根据此逻辑进行编写

如果当前需要删除的节点左为空,则令该节点的父节点指向该节点的右节点

				if (cur->_left == nullptr){if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}delete cur;return true;}else if (cur->_right == nullptr){if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}delete cur;return true;}

3.有两个子节点的节点                                                                                        

若要删除拥有两个子节点的节点

需要找到一个节点,该节点要求满足比原节点的左子树大,比原节点的右子树小

可以选择的节点是  左子树的最大节点 或  右子树的最小节点

左子树的最大节点一定 大于等于 原节点的左子节点(左节点的最右节点)

又一定比当前节点的右子节点小(大的节点都在右子树)

右子树的最小节点同理

// 删除多个子节点的节点
else
{// 可以找右子树的最小节点或左子树的最大节点(右子树最左侧的节点或左子树最右的节点)Node* rightMinP = cur; // 右子树最小节点的父节点Node* rightMin = cur->_right;while (rightMin->_left){rightMinP = rightMin;rightMin = rightMin->_left;}// 用最左节点给该节点赋值cur->_key = rightMin->_key;// 随后删除最左节点(相当于两个节点进行了交换)// 判断需要被删除的节点是P的左节点还是右节点(由于左可能为空,所以最左节点未必是左节点)if (rightMinP->_left == rightMin){rightMinP->_left = rightMin->_right;}else{rightMinP->_right = rightMin->_right;}
}

源代码

#pragma once
#include <iostream>
using namespace std;template<class K>
struct BSTNode // 二叉树节点
{K _key;BSTNode<K>* _left;BSTNode<K>* _right;BSTNode (const K& key) // 构造函数:_key(key),_left(nullptr),_right(nullptr){ }
};template<class K>
class BSTree 
{typedef BSTNode<K> Node;
public:bool Insert(const K& key) // 插入节点{if (_root == nullptr) // 处理空树{_root = new Node(key);return true;}Node* parent = nullptr; // 父亲节点,用于存储当前节点的父节点Node* cur = _root;while (cur) // 寻找适合的位置{if (cur->_key < key){parent = cur; // 每次当前节点向下走时,存储当前节点为父节点cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else // 如果存在相同大小的节点就返回false,插入失败{return false;}}//通过与父节点比较大小,将节点插入适当位置cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}bool Search(const K& key) // 搜索节点{Node* cur = _root;while (cur) // 当节点没有走完{if (cur->_key < key) // key比当前节点大,则向右走找更大的节点{cur = cur->_right;}else if (cur->_key > key) // 后续同理{cur = cur->_left;}else // 直到找到为止{return true;}}return false; // 找不到就返回false}void InOrder() // 遍历子函数{_InOrder(_root);}bool Erase(const K& key) // 删除节点{Node* parent = nullptr;// 先找到需要删除的节点Node* cur = _root;while (cur) // 当节点没有走完{if (cur->_key < key) // key比当前节点大,则向右走找更大的节点{parent = cur;cur = cur->_right;}else if (cur->_key > key) // 后续同理{parent = cur;cur = cur->_left;}else // 直到找到为止,进行删除{// 进行删除// 删除0-1个子节点的节点if (cur->_left == nullptr){// 当删除根节点时需要特殊处理if (parent == nullptr){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;return true;}else if (cur->_right == nullptr){if (parent == nullptr){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;return true;}// 删除多个子节点的节点else{// 可以找右子树的最小节点或左子树的最大节点(右子树最左侧的节点或左子树最右的节点)Node* rightMinP = cur; // 右子树最小节点的父节点Node* rightMin = cur->_right;while (rightMin->_left){rightMinP = rightMin;rightMin = rightMin->_left;}// 用最左节点给该节点赋值cur->_key = rightMin->_key;// 随后删除最左节点(相当于两个节点进行了交换)// 判断需要被删除的节点是P的左节点还是右节点(由于左可能为空,所以最左节点未必是左节点)if (rightMinP->_left == rightMin){rightMinP->_left = rightMin->_right;}else{rightMinP->_right = rightMin->_right;}}}}// 没找到return false;}private:Node* _root = nullptr;void _InOrder(Node* root) // 遍历{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}
};