监督分类——最小距离分类、最大似然分类、支持向量机

本文将详细介绍三种常见的监督分类方法：最小距离分类器、最大似然分类器和支持向量机（SVM）。每种方法都会包括原理、数学公式、具体例子和Python代码（含原图及分类结果可视化）。

---

1. 最小距离分类器（Minimum Distance Classifier）

原理

最小距离分类器是一种基于距离度量的简单分类方法。它将每个样本与各类别的均值（中心）计算欧氏距离，样本分配给距离最近的类别。适用于各类别内部方差相等且协方差为零的情况。

数学公式

对于样本 ( x ) 和第 ( i ) 类均值：
$$d_i(x)=\sqrt{(x-{\mu }_i{)}^T(x-{\mu }_i)}$$
样本 ( x ) 属于距离最近的类别 i，即：
$$i^{\ast }=\arg \underset{i}{\min }{d}_i(x)$$

Python代码示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.decomposition import PCA# 加载数据，用的是乳腺癌数据集
data = load_breast_cancer()
X = data.data
y = data.target# 用PCA降维到二维，便于可视化
pca = PCA(n_components=2)
X2 = pca.fit_transform(X)# 计算每一类的均值
mu0 = X2[y == 0].mean(axis=0)
mu1 = X2[y == 1].mean(axis=0)def min_distance_classifier(X, mus):dists = np.array([np.linalg.norm(X - mu, axis=1) for mu in mus])return np.argmin(dists, axis=0)pred = min_distance_classifier(X2, [mu0, mu1])# 可视化
fig, axes = plt.subplots(1, 2, figsize=(11, 4))
axes[0].scatter(X2[:, 0], X2[:, 1], c=y, cmap='bwr', label='True')
axes[0].set_title('Original')
axes[0].set_xlabel('PC1')
axes[0].set_ylabel('PC2')axes[1].scatter(X2[:, 0], X2[:, 1], c=pred, cmap='bwr')
# axes[1].scatter([mu0[0], mu1[0]], [mu0[1], mu1[1]], c=['red', 'blue'], marker='*', s=200, label='Mean')
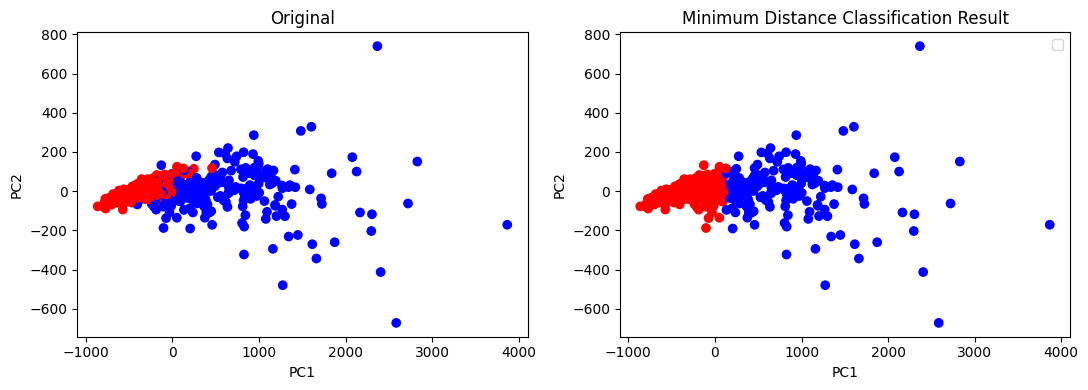
axes[1].set_title('Minimum Distance Classification Result')
axes[1].set_xlabel('PC1')
axes[1].set_ylabel('PC2')
axes[1].legend()
plt.tight_layout()
plt.show()

结果：

---

2. 最大似然分类器（Maximum Likelihood Classifier）

原理

最大似然分类器基于贝叶斯判别原理。对于每个样本，计算其属于各类别的概率密度（通常假设高斯分布），并结合先验概率，选取后验概率最大的类别。

数学公式

后验概率：
$$p({\omega }_i|x)\propto p(x|{\omega }_i)P({\omega }_i)$$
如果各类别先验相同，则只需比较似然项 ( p(x|\omega_i) )。常见情况下，假设各类别为高斯分布：
$$p(x|{\omega }_i)=\frac{1}{(2\pi {)}^{d/2}|{\Sigma }_i{|}^{1/2}}\exp \left(-\frac{1}{2}(x-{\mu }_i{)}^T{\Sigma }_i^{-1}(x-{\mu }_i)\right)$$

Python代码示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.decomposition import PCA
from scipy.stats import multivariate_normaldata = load_breast_cancer()
X = data.data
y = data.target# PCA降到二维
pca = PCA(n_components=2)
X2 = pca.fit_transform(X)# 估计高斯分布参数
mu0, cov0 = X2[y == 0].mean(axis=0), np.cov(X2[y == 0], rowvar=False)
mu1, cov1 = X2[y == 1].mean(axis=0), np.cov(X2[y == 1], rowvar=False)def ml_classifier(X, params):probs = [multivariate_normal(mean=mu, cov=cov).pdf(X) for mu, cov in params]return np.argmax(np.stack(probs, axis=1), axis=1)pred = ml_classifier(X2, [(mu0, cov0), (mu1, cov1)])fig, axes = plt.subplots(1, 2, figsize=(11, 4))
axes[0].scatter(X2[:, 0], X2[:, 1], c=y, cmap='bwr')
axes[0].set_title('Original Data (PCA Projection)')
axes[0].set_xlabel('PC1')
axes[0].set_ylabel('PC2')axes[1].scatter(X2[:, 0], X2[:, 1], c=pred, cmap='bwr')
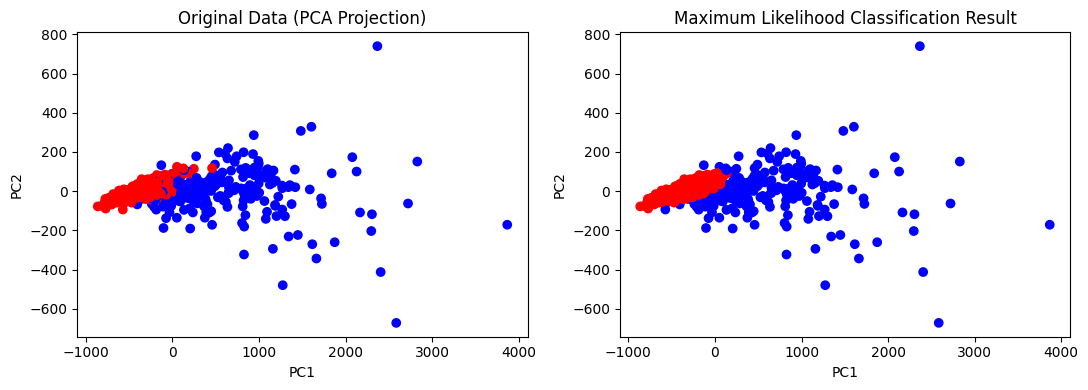
axes[1].set_title('Maximum Likelihood Classification Result')
axes[1].set_xlabel('PC1')
axes[1].set_ylabel('PC2')
plt.tight_layout()
plt.show()

结果：

---

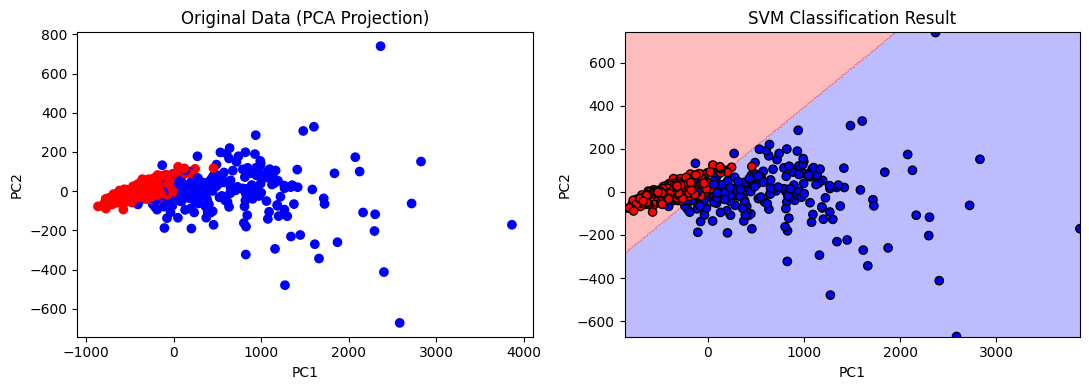
3. 支持向量机（SVM）

原理

SVM是一种判别式模型，通过寻找一个最优超平面，将不同类别样本分开，并最大化两类之间的间隔。对于线性可分情况，目标是：
$$\underset{w,b}{\min }\frac{1}{2}\Vert w{\Vert }^2$$
约束条件：
$$y_i(w^T{x}_i+b)\ge 1$$
对于非线性情况，可通过核函数映射到高维空间。

Python代码示例

用scikit-learn的SVM对两类数据进行分类并可视化决策边界。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.decomposition import PCA
from sklearn.svm import SVCdata = load_breast_cancer()
X = data.data
y = data.target# PCA降维
pca = PCA(n_components=2)
X2 = pca.fit_transform(X)clf = SVC(kernel='linear')
clf.fit(X2, y)
pred = clf.predict(X2)def plot_decision_boundary(clf, X, y, ax):x_min, x_max = X[:, 0].min()-1, X[:, 0].max()+1y_min, y_max = X[:, 1].min()-1, X[:, 1].max()+1xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300), np.linspace(y_min, y_max, 300))Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)ax.contourf(xx, yy, Z, alpha=0.3, cmap='bwr')ax.scatter(X[:, 0], X[:, 1], c=y, cmap='bwr', edgecolors='k')ax.set_title('SVM Classification Result')ax.set_xlabel('PC1')ax.set_ylabel('PC2')fig, axes = plt.subplots(1, 2, figsize=(11, 4))
axes[0].scatter(X2[:, 0], X2[:, 1], c=y, cmap='bwr')
axes[0].set_title('Original Data (PCA Projection)')
axes[0].set_xlabel('PC1')
axes[0].set_ylabel('PC2')plot_decision_boundary(clf, X2, y, axes[1])
plt.tight_layout()
plt.show()

结果：

---