【论文阅读】-《HopSkipJumpAttack: A Query-Efficient Decision-Based Attack》

HopSkipJumpAttack：一种查询高效的基于决策的攻击

Jianbo Chen∗ Michael I. Jordan∗ Martin J. Wainwright∗,†
University of California, Berkeley∗ Voleon Group†
{jianbochen@, jordan@cs., wainwrig@}berkeley.edu
原文链接:https://arxiv.org/pdf/1904.02144

摘要

对训练模型进行基于决策的对抗攻击的目标是，仅通过观察目标模型返回的输出标签来生成对抗样本。我们开发了 HopSkipJumpAttack，这是一族基于一种新颖的、利用决策边界二元信息估计梯度方向的算法。所提出的算法族包括分别针对 ${\ell }_2$ 和 ${\ell }_{\infty }$ 相似性度量优化的非目标攻击和目标攻击。为所提出的算法和梯度方向估计提供了理论分析。实验表明，HopSkipJumpAttack 所需的模型查询次数显著少于几种最先进的基于决策的对抗攻击。它在攻击几种广泛使用的防御机制时也取得了具有竞争力的性能。

I 引言

尽管深度神经网络在各种任务上取得了最先进的性能，但已被证明易受对抗样本的攻击——即恶意扰动的样本，在人类感知上几乎与原始样本相同，但会导致模型做出错误决策 [1]。神经网络对对抗样本的脆弱性暗示着在自动驾驶汽车、机器人技术、金融服务和刑事司法等具有现实世界后果的应用中存在安全风险；此外，它也突显了人类学习与现有基于机器的系统之间的根本差异。因此，研究对抗样本对于识别当前机器学习算法的局限性、提供鲁棒性度量、调查潜在风险以及提出提高模型鲁棒性的方法都是必要的。

近年来，关于设计生成对抗样本的新算法的研究层出不穷 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]。对抗样本可以根据至少三个不同的标准进行分类：相似性度量、攻击目标和威胁模型。常用的相似性度量是 ${\ell }_p$-距离（p∈{0,2,∞}p\in\{0,2,\infty\}p∈{0,2,∞}），表示对抗样本与原始样本之间的距离。攻击目标可以是非目标攻击或目标攻击。非目标攻击的目标是扰动输入以引起任何类型的错误分类，而目标攻击的目标是将模型的决策更改为预定的目标类别。改变损失函数可以在两种类型的攻击之间切换 [3, 5, 6]。

实践中最重要的标准可能是威胁模型，主要有两种类型：白盒攻击和黑盒攻击。在白盒设置下，攻击者拥有对模型的完全访问权限，包括其结构和权重。在此设置下，生成对抗样本通常被表述为一个优化问题，可以通过将错误分类损失视为正则化项 [1, 6] 或通过将其对偶作为约束优化问题来解决 [2, 3, 7]。在黑盒设置下，攻击者只能访问目标模型的输出。根据是否可以访问给定输入的完整概率或仅标签，黑盒攻击进一步分为基于分数的攻击和基于决策的攻击。图 1 展示了三种威胁模型中每种模型可访问目标模型组件的示意图。Chen 等人 [8] 和 Ilyas 等人 [9, 10] 引入了使用零阶梯度估计来制作对抗样本的基于分数的方法。

最实用的威胁模型是攻击者仅能访问决策的情况。广泛研究的一种基于决策的攻击是基于迁移的攻击。Liu 等人 [11] 表明，在白盒攻击中，在深度神经网络集成上生成的对抗样本可以迁移到一个未见过的神经网络。Papernot 等人 [12, 13] 提出通过查询目标模型来训练一个替代模型。然而，基于迁移的攻击通常需要精心设计的替代模型，甚至需要访问部分训练数据。此外，它们可以通过在由来自多个静态预训练模型的对抗样本增强的数据集上进行训练来防御 [17]。在

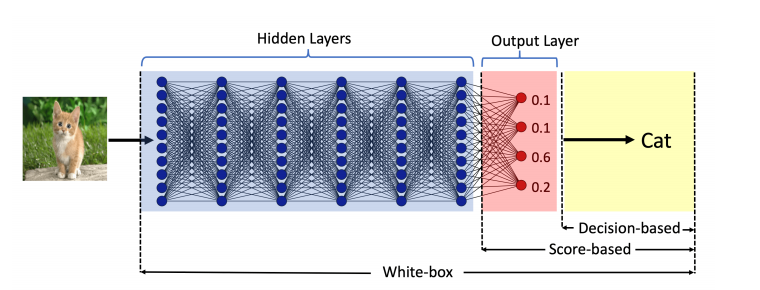
图 1：三种威胁模型中每种模型可访问目标模型组件的示意图。白盒威胁模型假设可以访问整个模型；基于分数的威胁模型假设可以访问输出层；基于决策的威胁模型假设仅能访问预测的标签。

最近的工作中，Brendel 等人 [14] 提出了边界攻击 (Boundary Attack)，该方法通过拒绝采样生成对抗样本。该方法既不依赖于训练数据，也不依赖于可迁移性假设，却实现了与最先进的白盒攻击（如 C&W 攻击 [6]）相当的性能。然而，边界攻击的一个局限性是它仅针对 ${\ell }_2$-距离制定。此外，它需要相对大量的模型查询，这使其在实际应用中不切实际。

在模型查询预算有限的情况下，评估机器学习系统在基于决策的攻击下的脆弱性更为现实。在线图像分类平台通常会在特定时间段内设置允许的查询次数上限。例如，Google 的云视觉 API 目前每分钟允许 1,800 次请求。因此，查询效率低下会导致时钟时间效率低下，并阻止攻击者发起大规模攻击。系统也可能被设置为将短时间内输入大量相似查询的行为识别为欺诈，这将自动过滤掉查询效率低下的基于决策的攻击。最后但同样重要的是，较小的查询预算直接意味着评估和研究的成本更低。查询高效的算法有助于节省评估公共平台鲁棒性的成本，因为攻击者进行的每次查询都会产生成本。它也有助于促进对抗脆弱性的研究，因为这种不需要访问模型细节的基于决策的攻击，可以作为评估新防御机制的一个简单高效的第一步，正如我们将在第 V-B 节和附录 C 中看到的那样。

在本文中，我们在优化框架下研究基于决策的攻击，并提出了一种新颖的算法族，用于生成针对 ${\ell }_2$ 距离或${\ell }_{\infty }$ 距离进行最小距离优化的目标和非目标对抗样本。该算法族本质上是迭代的，每次迭代涉及三个步骤：梯度方向估计、通过几何级数进行的步长搜索以及通过二分搜索进行的边界搜索。对优化框架和梯度方向估计进行了理论分析，这不仅为选择超参数提供了见解，而且为所提出算法中的关键步骤提供了动机。我们将该算法称为 HopSkipJumpAttack¹。总之，我们的贡献如下：

• 我们提出了一种新颖的、仅基于访问模型决策的决策边界梯度方向的无偏估计方法，并提出了控制因偏离边界而产生的误差的方法。
• 我们基于所提出的估计和我们的分析，设计了一个算法族 HopSkipJumpAttack，它是无超参数的、查询高效的，并且配备了收敛性分析。
• 我们通过大量实验证明了我们的算法在效率上优于几种最先进的基于决策的攻击。
• 通过评估防御性蒸馏、基于区域的分类、对抗训练和输入二值化等几种防御机制，我们建议我们的攻击可以作为研究人员评估新防御机制的简单高效的第一步。

路线图。 在第 II 节中，我们描述了先前关于基于决策的对抗攻击的工作及其与我们算法的关系。我们还讨论了我们的算法与零阶优化的联系。在第 III 节中，我们提出并分析了一种需要访问梯度信息的新颖迭代算法。每一步都从边界执行梯度更新，然后再次投影回边界。在第 IV 节中，我们引入了一种新颖的、在边界处渐近无偏的梯度方向估计，以及一种逼近边界的二分搜索过程。我们还讨论了如何控制偏离边界带来的误差。该分析启发了一种基于决策的算法，HopSkipJumpAttack（算法 2）。实验结果在第 V 节提供。我们在第 VI 节结束，讨论未来的工作。

II 相关工作

基于决策的攻击

与我们的工作最相关的是 Brendel 等人 [14] 提出的边界攻击 (Boundary Attack) 方法。边界攻击是一种基于拒绝采样的迭代算法，初始化为一个位于目标类中的图像。在每一步中，从提议分布中采样一个扰动，该扰动减少了扰动图像到原始输入的距离。如果扰动后的图像仍处于目标类中，则保留该扰动；否则，丢弃该扰动。边界攻击在深度神经网络的图像分类上取得了与最先进的白盒攻击相当的性能。然而，其实际应用的关键障碍是需要大量的模型查询。在实践中，制作一个对抗样本所需的模型查询次数直接决定了基于决策的攻击所构成威胁的级别。边界攻击效率低下的一个来源是拒绝偏离目标类的扰动。在我们的算法中，这些扰动被用于梯度方向的估计。

已经提出了几种其他的基于决策的攻击来提高效率。Brunner 等人 [15] 引入了有偏边界攻击 (Biased Boundary Attack)，该方法通过将低频随机噪声与替代模型的梯度相结合来偏置采样过程。
有偏边界攻击能够显著减少模型查询次数。然而，与其他基于迁移的攻击一样，它依赖于替代模型和目标模型之间的可迁移性。我们的算法不依赖于额外的可迁移性假设。相反，它通过将丢弃的信息利用到梯度方向估计中，实现了对边界攻击的显著改进。Ilyas 等人 [9] 在仅标签设置下提出了 有限攻击 (Limited attack)，该方法通过基于新颖代理分数估计梯度来直接执行投影梯度下降。Cheng 等人 [16] 引入了 Opt 攻击 (Opt attack)，该方法将原始问题转换为连续版本，并通过随机零阶梯度更新来解决新问题。我们的算法通过一种新颖的梯度方向估计直接处理原始问题，从而在查询效率上优于有限攻击和 Opt 攻击。HopSkipJumpAttack 中的大多数模型查询是以小批量进行的，这也导致其时钟时间效率优于边界攻击。

零阶优化

零阶优化 (Zeroth-order optimization) 指的是仅基于访问函数值 $f(x)$（而不是梯度值 $\nabla f(x)$）来优化函数 $f$ 的问题。此类问题在凸优化和 Bandit（赌博机）文献中已被广泛研究。Flaxman 等人 [18] 研究了 Bandit 凸优化中梯度的一点随机估计。Agarwal 等人 [19] 以及 Nesterov 和 Spokoiny [20] 证明了通过使用两个函数评估来估计梯度可以实现更快的收敛。Duchi 等人 [21] 通过使用两点梯度估计的镜像下降法，建立了凸零阶优化的最优速率。零阶算法已被应用于基于分数的威胁模型下生成对抗样本 [8, 9, 10]。后续工作 [22] 提出并分析了一种基于方差缩减随机梯度估计的算法。

我们将基于决策的攻击表述为一个优化问题。我们提出的算法的核心组成部分是梯度方向估计，其设计灵感来自零阶优化。然而，基于决策的攻击问题比零阶优化更具挑战性，本质上是因为我们只能从目标模型的输出标签中获得二元信息，而不是函数值。

III 优化框架

在本节中，我们描述一个用于为以下类型的 $m$ 元分类模型寻找对抗实例的优化框架。第一个组件是一个判别函数 $F:{\mathbb{R}}^d\to {\mathbb{R}}^m$，它接受输入 $x\in [0,1{]}^d$ 并产生输出 y∈Δm:={y∈[0,1]m∣∑c=1myc=1}y\in\Delta_{m}:=\{y\in[0,1]^{m} \mid \sum_{c=1}^{m}y_{c}=1\}y∈Δm​:={y∈[0,1]m∣∑c=1m​yc​=1}。输出向量 $y=(F_1(x),\dots ,F_m(x))$ 可以看作是标签集 [m]={1,…,m}[m]=\{1,\ldots,m\}[m]={1,…,m} 上的概率分布。基于函数 $F$，分类器 $C:{\mathbb{R}}^d\to [m]$ 将输入 $x$分配给概率最大的类别——即，

$$C(x):=\arg \underset{c\in [m]}{\max }{F}_c(x).$$

我们研究非目标和目标两种类型的对抗攻击。给定某个输入 $x^{\ast }$，非目标攻击的目标是将原始分类器决策 $c^{\ast }:=C(x^{\ast })$ 更改为任何 c∈[m]\{c∗}c\in[m]\backslash\{c^{*}\}c∈[m]\{c∗}，而目标攻击的目标是将决策更改为某个预先指定的 c†∈[m]\{c∗}c^{\dagger}\in[m]\backslash\{c^{*}\}c†∈[m]\{c∗}。形式上，如果我们通过以下方式定义函数 $S_{x^{\ast }}:{\mathbb{R}}^d\to \mathbb{R}$：

$$S_{x^{\ast }}(x^{\prime }):=\{\begin{array}{ll}{\max }_{c\ne c^{\ast }}{F}_c(x^{\prime })-F_{c^{\ast }}(x^{\prime })& \text{(非目标)}\\ F_{c^{†}}(x^{\prime })-{\max }_{c\ne c^{†}}{F}_c(x^{\prime })& \text{(目标)}\end{array}$$ (1)

那么扰动的图像 $x^{\prime }$ 是成功的攻击当且仅当 $S_{x^{\ast }}(x^{\prime })>0$。成功和不成功的扰动图像之间的边界是

$$\mathrm{bd}(S_{x^{\ast }}):=\left\{z\in [0,1{]}^d\mid S_{x^{\ast }}(z)=0\right\}.$$

作为成功扰动的指示器，我们引入布尔值函数 ϕx∗:[0,1]d→{−1,1}\phi_{x^{*}}:[0,1]^{d}\rightarrow\{-1,1\}ϕx∗​:[0,1]d→{−1,1}：

$${\varphi }_{x^{\ast }}(x^{\prime }):=\mathrm{sign}\left(S_{x^{\ast }}(x^{\prime })\right)=\{\begin{array}{ll}1& \text{如果 Sx∗(x′)>0},\\ -1& \text{否则}.\end{array}$$

在基于决策的设置中可以访问此函数，因为它可以通过仅查询分类器 $C$来计算。对抗攻击的目标是生成一个扰动的样本 $x^{\prime }$，使得 ${\varphi }_{x^{\ast }}(x^{\prime })=1$，同时保持 $x^{\prime }$ 接近原始样本 $x^{\ast }$。这可以表述为优化问题

$$\underset{x^{\prime }}{\min }d(x^{\prime },x^{\ast })\text{满足约束}{\varphi }_{x^{\ast }}(x^{\prime })=1,$$ (2)

其中 $d$ 是量化相似性的距离函数。过去工作中研究的 $d$ 的标准选择包括通常的 ${\ell }_p$-范数，其中 p∈{0,2,∞}p\in\{0,2,\infty\}p∈{0,2,∞}。

针对 ${\ell }_2$ 距离的迭代算法

考虑优化问题 (2) 使用 ${\ell }_2$-范数 $d(x,x^{\ast })=\Vert x-x^{\ast }{\Vert }_2$ 的情况。我们首先指定一个可以访问梯度 $\nabla S_{x^{\ast }}$ 的迭代算法。给定一个初始向量 $x_0$ 使得 $S_{x^{\ast }}(x_0)>0$ 和一个步长序列 {ξt}t≥0\{\xi_{t}\}_{t\geq 0}{ξt​}t≥0​，它执行更新

$$x_{t+1}={\alpha }_t{x}^{\ast }+(1-{\alpha }_t)\left\{x_t+{\xi }_t\frac{\nabla S_{x^{\ast }}(x_t)}{\Vert \nabla S_{x^{\ast }}(x_t){\Vert }_2}\right\},$$ (3)

其中${\xi }_t$ 是正步长。这里的线搜索参数 ${\alpha }_t\in [0,1]$ 被选择使得 $S_{x^{\ast }}(x_{t+1})=0$——也就是说，使得下一个迭代点 $x_{t+1}$ 位于边界上。选择此操作的动机是我们在第 IV 节中的梯度方向估计仅在边界附近有效。
我们现在在二分类设置下，假设可以访问 $S_{x^{\ast }}$ 的梯度，分析该算法。假设函数$S_{x^{\ast }}$ 是二次可微的，且梯度局部 Lipschitz 连续，这意味着存在 $L>0$ 使得对于所有 x,y∈{z:∥z−x∗∥2≤∥x0−x∗∥2}x,y\in\{z:\|z-x^{*}\|_{2}\leq\|x_{0}-x^{*}\|_{2}\}x,y∈{z:∥z−x∗∥2​≤∥x0​−x∗∥2​}，我们有

$$\Vert \nabla S_{x^{\ast }}(x)-\nabla S_{x^{\ast }}(y){\Vert }_2\le L\Vert x-y{\Vert }_2,$$ (4)

此外，我们假设梯度在边界上远离零：存在一个正的 $\tilde{C}>0$ 使得对于任何 $z\in \mathrm{bd}(S_{x^{\ast }})$，有 $\Vert \nabla S_{x^{\ast }}(z)\Vert >\tilde{C}$。

我们根据角度度量分析更新 (3) 的行为：

$$r(x_t,x^{\ast }):=\cos \angle \left(x_t-x^{\ast },\nabla S_{x^{\ast }}(x_t)\right)$$
$$=\frac{⟨x_t-x^{\ast },\nabla S_{x^{\ast }}(x_t)⟩}{\Vert x_t-x^{\ast }{\Vert }_2\Vert \nabla S_{x^{\ast }}(x_t){\Vert }_2},$$

对应于 $x_t-x^{\ast }$ 和梯度 $\nabla S_{x^{\ast }}(x_t)$ 之间角度的余弦值。注意，条件 $r(x,x^{\ast })=1$ 成立当且仅当 $x$ 是优化问题 (2) 的一个驻点。以下定理保证，在合适的步长下，更新收敛到这样的驻点：

定理 1.: 在先前所述的 $S_{x^{\ast }}$ 条件下，假设我们使用步长 ${\xi }_t=\Vert x_t-x^{\ast }{\Vert }_2{t}^{-q}$（其中 $q\in \left(\frac{1}{2},1\right)$）计算更新 (3)。那么存在一个通用常数 $c$，使得

$$0\le 1-r(x_t,x^{\ast })\le c{t}^{q-1}\text{对于 t=1,2,…}$$ (5)

特别地，该算法收敛到问题 (2) 的一个驻点。

定理 1 为我们在下一节提出的算法中选择步长提供了一个方案。附录 B 中对所提出的方案进行了实验评估。该定理的证明通过建立目标值 $d(x_t,x^{\ast })$ 和 $r(x_t,x^{\ast })$ 之间的关系，并结合边界处的二阶泰勒近似来构建。详见附录 A-A。

扩展到${\ell }_{\infty }$-距离

我们现在描述如何扩展这些更新以最小化 ${\ell }_{\infty }$-距离。考虑点 $x$ 到以 $x^{\ast }$ 为中心、半径为${\alpha }_t$ 的球面的 ${\ell }_2$-投影：

$${\Pi }_{x^{\ast },{\alpha }_t}^2(x):=\underset{\Vert y-x^{\ast }{\Vert }_2\le {\alpha }_t}{\mathrm{argmin}}\Vert y-x{\Vert }_2={\alpha }_t{x}^{\ast }+(1-{\alpha }_t)x.$$ (6)

根据这个算子，我们基于 ${\ell }_2$ 的更新 (3) 可以等价地改写为

$$x_{t+1}={\Pi }_{x^{\ast },{\alpha }_t}^2\left(x_t+{\xi }_t\frac{\nabla S_{x^{\ast }}(x_t)}{\Vert \nabla S_{x^{\ast }}(x_t){\Vert }_2}\right).$$ (7)

这个视角允许我们将算法扩展到其他 ${\ell }_p$-范数（$p\ne 2$）。例如，在 $p=\infty$ 的情况下，我们可以定义 ${\ell }_{\infty }$-投影算子 ${\Pi }_{x^{\ast },\alpha }^{\infty }$。它在 $x^{\ast }$ 的邻域内执行逐像素裁剪，使得 ${\Pi }_{x^{\ast },\alpha }^{\infty }(x)$ 的第 $i$ 个元素是

Πx∗,α∞(x)i:=max⁡{min⁡{xi∗,xi∗+c},xi−c},\Pi^{\infty}_{x^{*},\alpha}(x)_{i}:=\max\left\{\min\{x_{i}^{*},x_{i}^{*}+c\}\, ,x_{i}-c\right\},Πx∗,α∞​(x)i​:=max{min{xi∗​,xi∗​+c},xi​−c},

其中 $c:=\alpha \Vert x-x^{\ast }{\Vert }_{\infty }$。我们通过迭代执行以下更新来提出我们算法的 ${\ell }_{\infty }$ 版本：

$$x_{t+1}={\Pi }_{x^{\ast },{\alpha }_t}^2(x_t+{\xi }_t\nabla S_{x^{\ast }}(x_t))$$

其中 ${\alpha }_t$被选择使得 $S_{x^{\ast }}(x_{t+1})=0$，并且 “sign” 返回向量的逐元素符号。在实践中，为了更快的收敛，我们使用梯度的符号，类似于之前的工作 [2, 3, 7]。

IV 基于新颖梯度估计的基于决策算法

我们现在将我们的过程扩展到基于决策的设置中，在这个设置中我们只能访问布尔值函数 ${\varphi }_{x^{\ast }}(x)=\text{sign}(S_{x^{\ast }}(x))$——也就是说，该方法无法观察到底层的判别函数 $F$ 或其梯度。在本节中，当 $x_t\in \mathrm{bd}(S_{x^{\ast }})$（因此根据定义 $S_{x^{\ast }}(x_t)=0$）时，我们引入一种基于 ${\varphi }_{x^{\ast }}$ 的梯度方向估计。我们接着讨论如何逼近边界。然后我们讨论如何控制我们的估计因偏离边界而产生的误差。我们将用一个基于决策的算法来总结分析。

在边界上

给定一个迭代点 $x_t\in \mathrm{bd}(S_{x^{\ast }})$，我们建议通过蒙特卡洛估计来近似梯度 $\nabla S_{x^{\ast }}(x_t)$ 的方向：

$$\widetilde{\nabla S}(x_t,\delta ):=\frac{1}{B}\sum _{b=1}^B{\varphi }_{x^{\ast }}(x_t+\delta u_b)u_b,$$ (9)

其中 {ub}b=1B\{u_{b}\}_{b=1}^{B}{ub​}b=1B​ 是从 $d$ 维球面上的均匀分布中独立同分布地抽取的，$\delta$ 是一个小的正参数。（为简化符号，省略了此估计器对固定中心点 $x^{\ast }$ 的依赖。）

扰动参数 $\delta$ 是必要的，但会在估计中引入一种形式的偏差。我们的第一个结果控制这种偏差，并表明当 $\delta \to 0^{+}$ 时，$\widetilde{\nabla S}(x_t,\delta )$ 是渐近无偏的。

定理 2.: 对于一个边界点 $x_t$，假设 $S_{x^{\ast }}$ 在 $x_t$ 的邻域内具有 $L$-Lipschitz 梯度。那么 $\widetilde{\nabla S}(x_t,\delta )$ 和 $\nabla S_{x^{\ast }}(x_t)$ 之间角度的余弦值被以下不等式界定：

$$\cos \angle \left(\mathbb{E}[\widetilde{\nabla S}(x_t,\delta )],\nabla S_{x^{\ast }}(x_t)\right)\ge 1-\frac{9L^2{\delta }^2{d}^2}{8\Vert \nabla S(x_t){\Vert }_2^2}.$$ (10)
$$\underset{\delta \to 0}{\lim }\cos \angle \left(\mathbb{E}[\widetilde{\nabla S}(x_t,\delta )],\nabla S_{x^{\ast }}(x_t)\right)=1,$$ (11)

这表明该估计作为方向估计是渐近无偏的。

我们注意到定理 2 仅确立了所提出估计在边界处的渐近行为。这也启发了我们将在第 IV-B 节讨论的算法中的边界搜索步骤。定理 2 的证明从将单位球面划分为三个部分开始：沿梯度方向的上帽区、与梯度方向相反的下帽区以及两者之间的环带区。当 $\delta$ 很小时，来自环带区的误差可以被界定。有关此定理的证明，请参见附录 A-B。正如后续将看到的，扰动大小 $\delta$ 应选择与 $d^{-1}$ 成正比；详见第 IV-C 节。

逼近边界

所提出的估计 (9) 仅在边界处有效。我们现在描述如何通过二分搜索逼近边界。令 ${\tilde{x}}_t$ 表示应用投影算子 ${\Pi }_{x,{\alpha }_t}^p$ 之前的更新样本：

$${\tilde{x}}_t:=x_t+{\xi }_t{v}_t(x_t,{\delta }_t),\text{其中}$$ (12)
$$v_t(x_t,{\delta }_t)=\{\begin{array}{ll}\widetilde{\nabla S}(x_t,{\delta }_t)/\Vert \widetilde{\nabla S}(x_t,{\delta }_t){\Vert }_2,& \text{如果}p=2,\\ \text{sign}(\widetilde{\nabla S}(x_t,{\delta }_t)),& \text{如果}p=\infty ,\end{array}$$

其中 $\widetilde{\nabla S}$ 将在后面的方程 (16) 中引入，作为$\widetilde{\nabla S}$ 的方差缩减版本，而${\delta }_t$ 是第 $t$ 步的扰动大小。

我们希望 ${\tilde{x}}_t$ 位于与$x$ 相对的边界另一侧，以便可以进行二分搜索。因此，我们初始化 ${\tilde{x}}_0$ 在目标一侧 (${\varphi }_{x^{\ast }}({\tilde{x}}_0)=1$)，并设置$x_0:={\Pi }_{x,{\alpha }_0}^p({\tilde{x}}_0)$，其中${\alpha }_0$ 通过在 0 和 1 之间进行二分搜索来选择，以逼近边界，在 $x_0$ 位于目标一侧 (${\varphi }_{x^{\ast }}(x_0)=1$) 时停止。在第 $t$ 次迭代时，我们从位于目标一侧 (${\varphi }_{x^{\ast }}(x_t)=1$) 的 $x_t$ 开始。步长初始化为

$${\xi }_t:=\Vert x_t-x^{\ast }{\Vert }_p/\sqrt{t},$$ (13)

如定理 1 在 ${\ell }_2$ 情况下的建议，然后将其减半直到 ${\varphi }_{x^{\ast }}({\tilde{x}}_t)=1$，我们称之为 ${\xi }_t$ 的几何级数递减。找到合适的 ${\tilde{x}}_t$ 后，我们通过在 0 和 1 之间进行二分搜索来选择投影半径 ${\alpha }_t$ 以逼近边界，该搜索在满足 ${\varphi }_{x^{\ast }}(x_{t+1})=1$ 的 $x_{t+1}$ 处停止。完整的二分搜索见算法 1，其中二分搜索阈值 $\theta$ 设置为某个小的常数。

在这里插入图片描述

控制偏离边界的误差

二分搜索永远不会将 $x_{t+1}$ 精确放置在边界上。我们分析梯度方向估计的误差，并提出了两种减少误差的方法。

V-Ca 随机扰动大小的适当选择

首先，用于估计梯度方向的随机扰动大小 ${\delta }_t$ 被选择为图像尺寸 $d$ 和二分搜索阈值 $\theta$ 的函数。这与数值微分不同，在数值微分中 ${\delta }_t$ 的最优选择在舍入误差的量级上（例如，[23]）。下面我们将大 ${\delta }_t$ 引起的误差表征为 ${\tilde{x}}_t$ 到边界距离的函数，并推导出 ${\xi }_t$ 和 ${\delta }_t$ 的适当选择。实际上，利用 $S_{x^{\ast }}$ 在 $x_t$ 处的泰勒近似，我们有

$$S_{x^{\ast }}(x_t+{\delta }_{t}u)=S_{x^{\ast }}(x_t)+{\delta }_t⟨\nabla S_{x^{\ast }}(x_t),u⟩+\mathcal{O}({\delta }_t^2).$$

在边界 $S_{x^{\ast }}(x_t)=0$ 处，梯度近似的误差在 $\mathcal{O}({\delta }_t^2)$ 量级，通过将 ${\delta }_t$ 减小到平方根舍入误差的量级可以最小化此误差。然而，有限步二分搜索的结果 $x_t$接近边界，但并非精确地位于边界上。

当 ${\delta }_t$ 足够小以至于可以忽略二阶项时，一阶泰勒近似意味着

${\varphi }_{x^{\ast }}(x_t+{\delta }_{t}u)=-1$ 当且仅当 $x_t+{\delta }_{t}u$ 位于球冠$\mathcal{C}$ 上，其中

$$\mathcal{C}:=\left\{u\mid ⟨\frac{\nabla S_{x^{\ast }}(x_t)}{\Vert \nabla S_{x^{\ast }}(x_t){\Vert }_2},u⟩<-{\delta }_t^{-1}\frac{S_{x^{\ast }}(x_t)}{\Vert \nabla S_{x^{\ast }}(x_t){\Vert }_2}\right\}.$$

另一方面，在高维球面上，$u$ 的概率质量集中在赤道附近，这由以下不等式表征 [24]：

P(u∈C)≤2cexp⁡{−c22},其中 c=d−2Sx∗(xt)δt∥∇Sx∗(xt)∥2.\mathbb{P}(u\in\mathcal{C})\leq\frac{2}{c}\exp\{-\frac{c^{2}}{2}\},\text{其中 }c= \frac{\sqrt{d-2}S_{x^{*}}(x_{t})}{\delta_{t}\|\nabla S_{x^{*}}(x_{t})\|_{2}}.P(u∈C)≤c2​exp{−2c2​},其中 c=δt​∥∇Sx∗​(xt​)∥2​d−2​Sx∗​(xt​)​. (14)

将 $x_t$ 在 $x_t^{\prime }:={\Pi }_{\partial }^2(x_t)$（边界上的投影点）处进行泰勒展开得到

$$S_{x^{\ast }}(x_t)=\nabla S_{x^{\ast }}(x_t^{\prime }{)}^T(x_t-x_t^{\prime })+\mathcal{O}(\Vert x_t-x_t^{\prime }{\Vert }_2^2)$$
$$=\nabla S_{x^{\ast }}(x_t{)}^T(x_t-x_t^{\prime })+\mathcal{O}(\Vert x_t-x_t^{\prime }{\Vert }_2^2).$$

根据 Cauchy-Schwarz 不等式和 ${\ell }_2$-投影的定义，我们有

$$\begin{array}{rl}& |\nabla S_{x^{\ast }}(x_t{)}^T(x_t-x_t^{\prime })|\\ & \le \Vert \nabla S_{x^{\ast }}(x_t){\Vert }_2\Vert x_t-{\Pi }_{\partial }^2(x_t){\Vert }_2\\ & \le \{\begin{array}{ll}\Vert \nabla S_{x^{\ast }}(x_t){\Vert }_2\theta \Vert {\tilde{x}}_{t-1}-x^{\ast }{\Vert }_p,& \text{如果}p=2,\\ \Vert \nabla S_{x^{\ast }}(x_t){\Vert }_2\theta \Vert {\tilde{x}}_{t-1}-x^{\ast }{\Vert }_p\sqrt{d},& \text{如果}p=\infty .\end{array}\end{array}$$

这得到

$$c=\mathcal{O}(\frac{d^q\theta \Vert {\tilde{x}}_{t-1}-x^{\ast }{\Vert }_p}{{\delta }_t}),$$

其中$q=1-(1/p)$ 是对偶指数。为了避免测度集中导致的精度损失，我们令 ${\delta }_t=d^q\theta \Vert {\tilde{x}}_{t-1}-x^{\ast }{\Vert }_2$。为了使近似误差独立于维度 $d$，我们将$\theta$ 设置为 $d^{-q-1}$ 的量级，这样 ${\delta }_t$ 与$d^{-1}$ 成正比，正如定理 2 所建议的。这导致模型查询次数具有对数级的维度依赖性。在实践中，我们设置

$$\theta =d^{-q-1},{\delta }_t=d^{-1}\Vert {\tilde{x}}_{t-1}-x^{\ast }{\Vert }_p.$$ (15)

IV-Bb 梯度方向估计中方差缩减的基线

另一个误差来源是估计的方差，我们通过其协方差算子的迹来表征随机向量 $v\in {\mathbb{R}}^d$ 的方差：$\mathrm{Var}(v):={\sum }_{i=1}^d\mathrm{Var}(v_i)$。当 $x_t$ 偏离边界且${\delta }_t$ 不完全为零时，扰动样本在边界两侧的分布不均匀：

$$\left|\mathbb{E}[{\varphi }_{x^{\ast }}(x_t+{\delta }_{t}u)]\right|>0,$$

正如我们从方程 (14) 中看到的那样。为了尝试控制方差，我们在估计中引入一个基线 $\overline{{\varphi }_{x^{\ast }}}$：

$$\overline{{\varphi }_{x^{\ast }}}:=\frac{1}{B}\sum _{b=1}^B{\varphi }_{x^{\ast }}(x_t+\delta u_b),$$

这产生了以下估计：

$$\widehat{\nabla S}(x_t,\delta ):=\frac{1}{B-1}\sum _{b=1}^B({\varphi }_{x^{\ast }}(x_t+\delta u_b)-\overline{{\varphi }_{x^{\ast }}})u_b.$$(16)

可以很容易地观察到，该估计在期望上等于先前的估计，因此在边界处仍然是渐近无偏的：当 $x_t\in \text{bd}(S_{x^{\ast }})$ 时，我们有

$$\cos \angle \left(\mathbb{E}[\widehat{\nabla S}(x_t,\delta )],\nabla S_{x^{\ast }}(x_t)\right)\ge 1-\frac{9L^2{\delta }^2{d}^2}{8\Vert \nabla S(x_t){\Vert }_2^2},$$
$$\underset{\delta \to 0}{\lim }\cos \angle \left(\mathbb{E}[\widehat{\nabla S}(x_t,\delta )],\nabla S_{x^{\ast }}(x_t)\right)=1.$$

此外，当 $\mathbb{E}[{\varphi }_{x^{\ast }}(x_t+\delta u)]$ 偏离零时，基线的引入减少了方差。特别是，以下定理表明，每当 $|\mathbb{E}[{\varphi }_{x^{\ast }}(x_t+\delta u)]|=\Omega (B^{-\frac{1}{2}})$ 时，引入基线会减少方差。

定理 3.: 定义${\sigma }^2:=\mathrm{Var}({\varphi }_{x^{\ast }}(x_t+\delta u)u)$ 作为单点估计的方差，我们有

$$\mathrm{Var}(\widehat{\nabla S}(x_t,\delta ))<\mathrm{Var}(\widetilde{\nabla S}(x_t,\delta ))(1-\psi ),$$

其中

$$\psi =\frac{2}{{\sigma }^2(B-1)}\left(2B\mathbb{E}{\left[{\varphi }_{x^{\ast }}(x_t+\delta u)\right]}^2-1\right)-\frac{2B-1}{(B-1{)}^2}$$

证明参见附录 A-C。我们还在附录 B 中展示了当样本偏离边界时，我们对梯度方向估计的实验评估，结果表明我们提出的 ${\delta }_t$ 选择和基线的引入在估计梯度方面带来了性能提升。

HopSkipJumpAttack

我们现在将上述分析结合成一个迭代算法 HopSkipJumpAttack。它被初始化为
对于非目标攻击，初始化为目标类中的一个样本；对于目标攻击，初始化为一个与均匀噪声混合并被错误分类的样本。算法的每次迭代包含三个部分。首先，通过二分搜索（算法 1）将上一次迭代的迭代点推向边界。其次，通过方程 (16) 估计梯度方向。第三，沿着梯度方向的更新步长根据定理 1 初始化为方程 (13)，并通过几何级数递减，直到扰动成功。下一次迭代从将扰动后的样本再次投影回边界开始。完整的流程总结在算法 2 中。图 2 直观地展示了在 ${\ell }_2$ 情况下的三个步骤。对于所有实验，我们将批量大小初始化为 $100$，并随 $\sqrt{t}$ 线性增加，以便估计的方差随 $t$ 减小。当输入域在实际应用中有界时，默认在每一步执行裁剪操作。

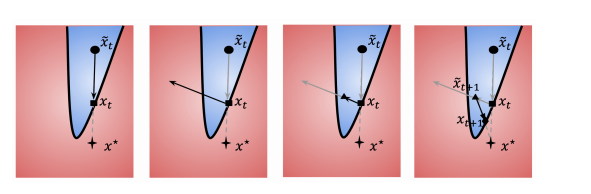
图2：HopSkipJumpAttack 的直观解释
(a) 执行二分搜索以定位决策边界，并更新 ${\tilde{x}}_t\to x_t$。
(b) 在边界点 $x_t$ 处估计梯度方向。
(c) 沿梯度方向进行几何级数跳跃，并更新 $x_t\to {\tilde{x}}_{t+1}$。
(d) 对更新点执行二分搜索，最终更新 ${\tilde{x}}_{t+1}\to x_{t+1}$。

V 实验

在本节中，我们对 HopSkipJumpAttack 进行实验分析。我们在图像分类任务上，将 HopSkipJumpAttack 的效率与几种先前提出的基于决策的攻击进行了比较。此外，我们在我们的攻击方法下评估了三种防御机制的鲁棒性。所有实验均在 Tesla K80 GPU 上进行，代码可在线获取²。我们的算法也可在 CleverHans [25] 和 Foolbox [26] 上使用，这是两个用于为机器学习模型制作对抗样本的流行 Python 包。

效率评估

基线方法： 我们将 HopSkipJumpAttack 与三种最先进的基于决策攻击进行比较：边界攻击 (Boundary Attack) [14]、有限攻击 (Limited Attack) [9] 和 Opt 攻击 (Opt Attack) [16]。我们使用这三种算法的公开源代码实现，并采用建议的超参数。根据 Ilyas 等人 [9]，有限攻击仅包含在目标${\ell }_{\infty }$ 设置下。

数据和模型： 为了全面评估 HopSkipJumpAttack，我们使用了广泛的数据和模型，具有不同的图像尺寸、数据集大小、任务复杂度级别和模型结构。

实验在四个图像数据集上进行：MNIST、CIFAR-10 [27]、CIFAR-100 [27] 和 ImageNet [28]，使用标准的训练/测试分割 [29]。这四个数据集具有不同的图像尺寸和类别数量。MNIST 包含 70K 张 $28\times 28$ 的 0-9 手写数字灰度图像。CIFAR-10 和 CIFAR-100 均由 $32\times 32\times 3$ 的图像组成。CIFAR-10 有 10 个类别，每个类别 6K 张图像；CIFAR-100 有 100 个类别，每个类别 600 张图像。ImageNet 有 $1,000$ 个类别。ImageNet 中的图像被缩放到 $224\times 224\times 3$。对于 MNIST、CIFAR-10 和

表 I：不同模型查询次数下的中值距离。在给定模型查询次数下较小的中值距离以粗体显示。BA 和 HSJA 分别代表边界攻击 (Boundary Attack) 和 HopSkipJumpAttack。

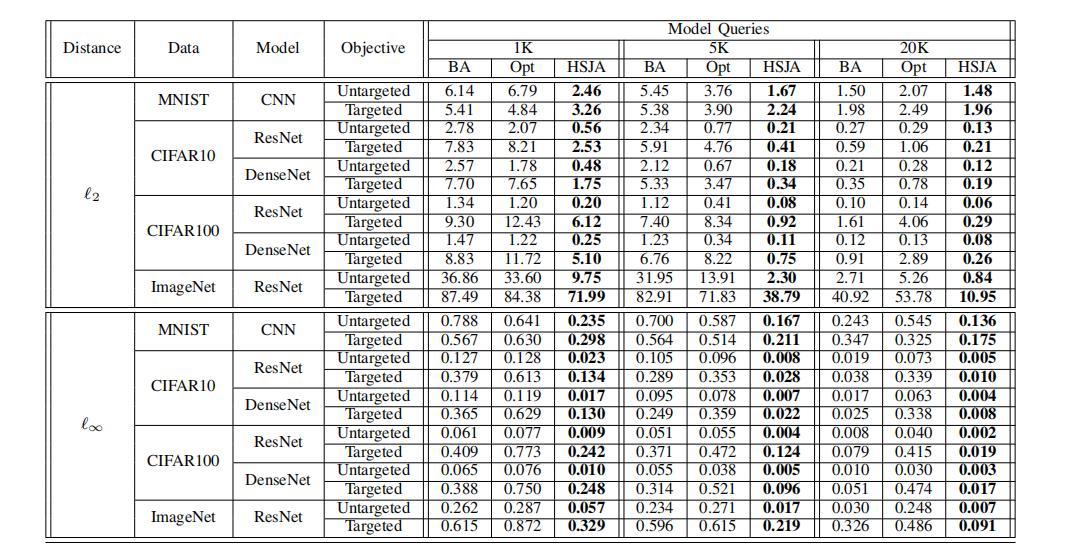
CIFAR-100，使用了 $1,000$ 张正确分类的测试图像，这些图像从测试数据集中随机抽取，并均匀分布在各个类别中。对于 ImageNet，我们使用了 $100$ 张正确分类的测试图像，均匀分布在 10 个随机选择的类别中。该选择方案遵循 Metzen 等人 [30] 的方法以确保可复现性。

我们还使用了不同结构的模型，从简单到复杂。对于 MNIST，我们使用一个简单的卷积网络，由两个卷积层组成，后跟一个具有 $1024$ 个单元的隐藏密集层。两个卷积层分别有$32,64$ 个滤波器，每个后面都跟着一个最大池化层。对于 CIFAR-10 和 CIFAR-100，我们分别训练了一个 $20$ 层的 ResNet [31] 和一个$121$ 层的 DenseNet [32]，均采用规范网络结构 [29]。对于 ImageNet，我们使用一个预训练的 $50$ 层 ResNet [31]。所有模型在各自的数据集上都达到了接近最先进的准确率。所有像素被缩放到 $[0,1]$ 范围内。对于所有实验，我们默认将所有算法生成的扰动图像裁剪到输入域 $[0,1]$ 内。

初始化： 对于非目标攻击，我们通过将原始图像与均匀随机噪声混合来初始化所有攻击，并逐渐增加均匀噪声的权重直到它被错误分类，这个过程在 Foolbox [26] 中可用，作为边界攻击的默认初始化。对于目标攻击，目标类别从错误标签中均匀采样。从测试集中随机采样一张属于目标类别的图像作为初始化。所有攻击使用相同的目标类别和相同的初始化图像。

度量标准： 第一个度量标准是测试图像子集上扰动样本与原始样本之间的中值 ${\ell }_p$ 距离，这在以前的工作中常用，例如 Carlini 和 Wagner [6]。Brendel 等人 [14] 使用了一个按图像维度归一化的版本来评估边界攻击。${\ell }_2$ 距离可以这样解释：给定一个大小为 $h\times w\times 3$ 的字节图像，在缩放后的输入图像上大小为 $d$ 的 ${\ell }_2$ 距离扰动相当于原始图像上平均 $\lceil d/\sqrt{h\times w\times 3}\ast 255\rceil$ 比特的扰动（在 $[0,255]$ 范围内）。${\ell }_{\infty }$ 距离大小为 $d$ 的扰动相当于原始图像上所有像素最大 $\lceil 255\cdot d\rceil$ 比特的扰动。

作为替代度量，我们还绘制了在给定有限模型查询预算下，两种算法在不同距离阈值下的成功率。如果扰动大小不超过给定的距离阈值，则定义对抗样本为成功。成功率可以直接关联到在给定

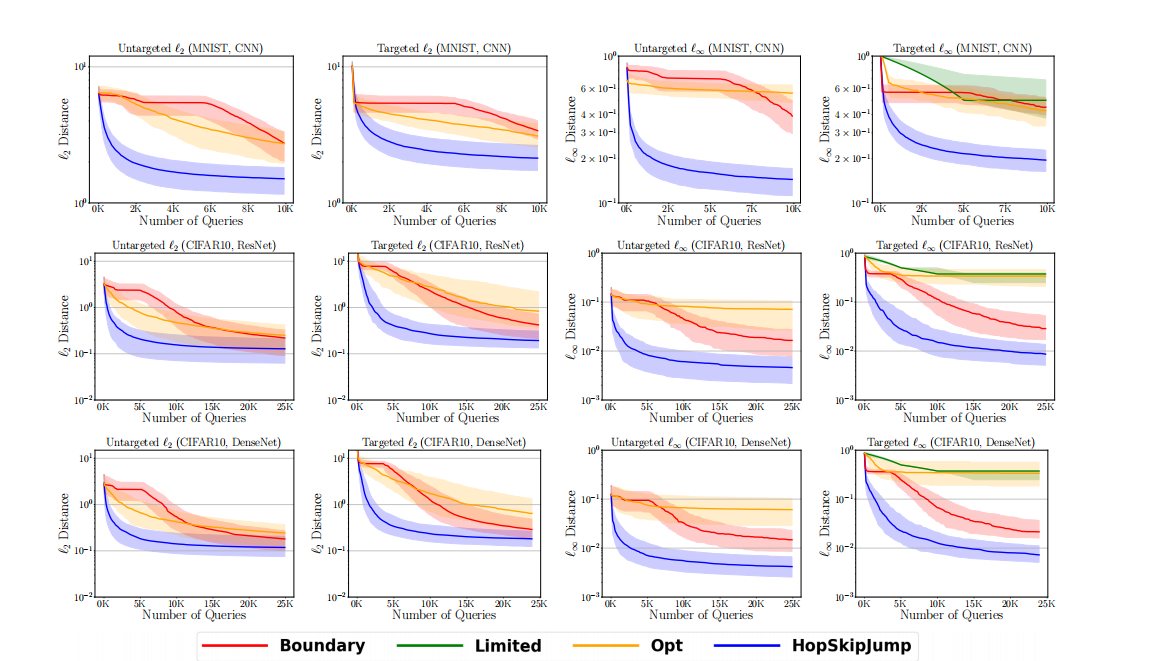
图 3：模型查询次数与中值距离的关系图，从上到下依次为：MNIST (CNN)、CIFAR-10 (ResNet)、CIFAR-10 (DenseNet)。第 1 列：非目标 ${\ell }_2$。第 2 列：目标 ${\ell }_2$。第 3 列：非目标 ${\ell }_{\infty }$。第 4 列：目标 ${\ell }_{\infty }$。

距离阈值下模型在扰动数据上的准确率：

扰动准确率 = 原始准确率 $\times$ (1 - 成功率)。 (17)

在整个实验中，由于计算资源有限，我们将每张图像的最大查询预算限制在 25,000 次，这是实际应用关注的设置。

结果： 图 3 和 图 4 显示了（对数尺度）中值距离随查询次数的变化，使用第一和第三四分位数作为下和上误差条。对于边界攻击、Opt 攻击和 HopSkipJumpAttack，表 I 总结了在所有距离类型、数据、模型和目标下，当查询次数固定为 1,000、5,000 和 20,000 时的中值距离。图 5 和 图 6 显示了成功率随距离阈值的变化。图 3 和 图 5 包含了在 MNIST (CNN)、CIFAR-10 (ResNet)、CIFAR-10 (DenseNet) 上的结果（从上到下）。图 4 和 图 6 包含了在 CIFAR-100 (ResNet)、CIFAR-100 (DenseNet)、ImageNet (ResNet) 上的结果（从上到下）。四列分别对应非目标${\ell }_2$、目标 ${\ell }_2$、非目标${\ell }_{\infty }$和目标${\ell }_{\infty }$ 攻击。

在有限查询次数下，HopSkipJumpAttack 能够在所有数据集上制作出与相应原始样本距离显著更小的对抗样本，其次是边界攻击和 Opt 攻击。作为一个具体例子，表 I 显示，针对 ${\ell }_2$ 优化的非目标 HopSkipJumpAttack 在 ResNet 模型上，使用 1,000 次查询时实现了 $0.559$ 的中值距离，这相当于平均每个像素低于 $3/255$。在相同的查询预算下，边界攻击和 Opt 攻击仅分别实现了 $2.78$ 和 $2.07$ 的中值 ${\ell }_2$-距离。对于 ${\ell }_{\infty }$ 攻击，效率差异更为显著。如图 5 所示，在使用 1,000 次查询、针对 ${\ell }_{\infty }$ 优化的非目标 HopSkipJumpAttack 下，大约 70% 的对抗样本的所有像素都在原始图像的 $8/255$ 邻域内，而边界攻击只有在 20,000 次查询后才能达到这个成功率。

通过比较图 3-6 的奇偶列，我们可以发现目标 HopSkipJumpAttack 需要比非目标攻击更多的查询次数才能达到相当的距离。这种现象在具有更多类别的 CIFAR-100 和 ImageNet 上更加明显。在相同查询次数下，非目标攻击和目标攻击的中值距离存在数量级差异（图 3 和 图 4）。对于针对 ${\ell }_2$ 优化的 HopSkipJumpAttack，非目标版本能够在 1,000 次查询内平均每个像素扰动 $4$比特来为 CIFAR-10 和 CIFAR-100 中 $70\%-90\%$ 的图像制作对抗图像，而目标版本需要 2,000-5,000 次查询。其他攻击即使在

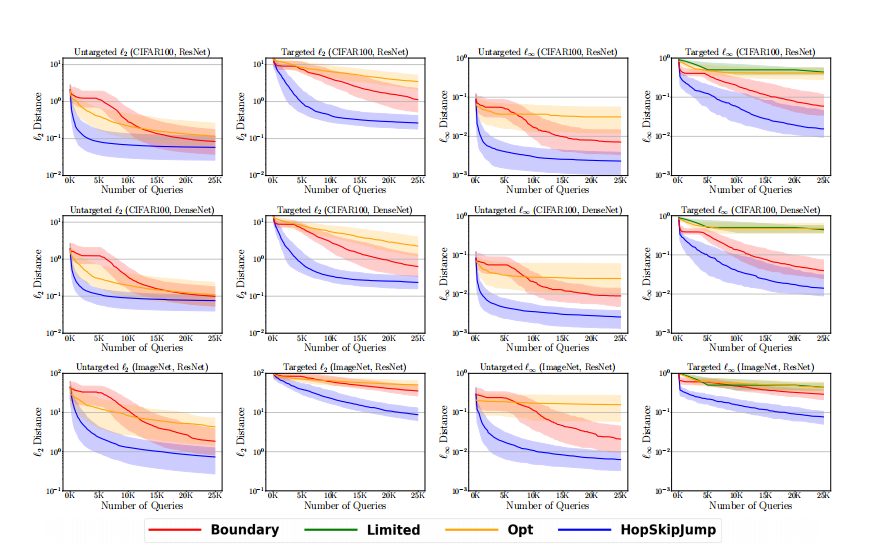
图 4：模型查询次数与中值距离的关系图，从上到下依次为：CIFAR-100 (ResNet)、CIFAR-100 (DenseNet)、ImageNet (ResNet)。第 1 列：非目标 ${\ell }_2$。第 2 列：目标 ${\ell }_2$。第 3 列：非目标 ${\ell }_{\infty }$。第 4 列：目标 ${\ell }_{\infty }$。

25,000 次查询后也无法达到可比的性能。在 ImageNet 上，针对 ${\ell }_2$ 优化的非目标 HopSkipJumpAttack 能够使用 1,000 次查询，以平均每个像素 $6$ 比特的扰动大小愚弄模型（接近 $50\%$ 的图像）；针对 ${\ell }_{\infty }$ 优化的非目标 HopSkipJumpAttack 在 1,000 次查询内，能将所有像素的最大扰动控制在 $16$ 比特以内（$50\%$ 的图像）。目标边界攻击直到大约 $25,000$ 次查询后才能将扰动大小控制到如此小的规模。一方面，更大的查询预算需求源于目标攻击比非目标攻击在形式上更强大。另一方面，这也是因为我们从目标类中的任意图像初始化目标 HopSkipJumpAttack。算法可能因这种初始化而陷入不良的局部极小值。未来的工作可以解决系统性方法以实现更好的初始化。

作为数据集和模型之间的比较，我们看到在 MNIST 上，对抗图像到其相应原始图像的距离通常比在 CIFAR-10 和 CIFAR-100 上更大，这在以前的工作中也观察到过（例如，[6]）。这可能是因为在更简单的任务上愚弄模型更困难。另一方面，HopSkipJumpAttack 在 MNIST 上以更少的查询次数收敛，如图 3 所示。在 ImageNet 上，即使在 $25,000$ 次查询后仍未收敛。我们推测查询预算与输入维度和决策边界的平滑度有关。我们还观察到，如果训练算法和数据集保持不变，模型结构的差异对基于决策的算法没有太大影响。对于在共同数据集上训练的 ResNet 和 DenseNet，基于决策的算法在制作对抗样本方面取得了可比的性能，尽管 DenseNet 的结构比 ResNet 更复杂。

与最先进的白盒目标攻击相比，C&W 攻击 [6] 在 CIFAR-10 上实现了平均 ${\ell }_2$-距离$0.33$，BIM [3] 在 CIFAR-10 上实现了平均 ${\ell }_{\infty }$-距离 $0.014$。目标 HopSkipJumpAttack 在 CIFAR-10 上使用 5K-10K 次模型查询实现了相当的距离，而无需访问模型细节。在 ImageNet 上，目标 C&W 攻击和 BIM 分别实现了 ${\ell }_2$-距离$0.96$ 和 ${\ell }_{\infty }$-距离 $0.01$。非目标 HopSkipJumpAttack 使用 $10,000-15,000$ 次查询实现了可比的性能。当查询预算限制在 $25,000$ 以内时，目标版本无法与目标白盒攻击相媲美。

在 CIFAR10 和 ImageNet 上针对 ${\ell }_2$ 距离优化的 HopSkipJumpAttack 的可视化轨迹可以在图 7 中找到。在 CIFAR-10 上，我们观察到非目标对抗样本可以在大约 $500$ 次查询内制作出来。

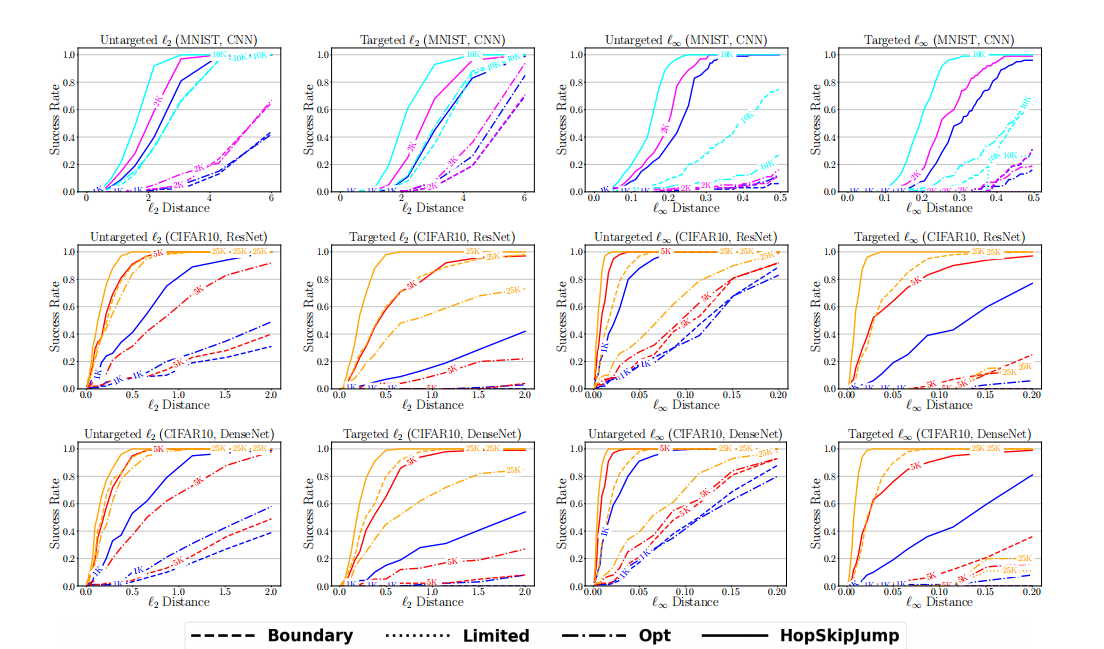
图 5：成功率与距离阈值的关系图，从上到下依次为：MNIST (CNN)、CIFAR-10 (ResNet)、CIFAR-10 (DenseNet)。第 1 列：非目标 ${\ell }_2$。第 2 列：目标 ${\ell }_2$。第 3 列：非目标 ${\ell }_{\infty }$。第 4 列：目标 ${\ell }_{\infty }$。

目标 HopSkipJumpAttack 能够在大约 $1,000-2,000$ 次查询内制作出人眼无法区分的针对性对抗样本。在 ImageNet 上，非目标 HopSkipJumpAttack 能够使用 $1,000$ 次查询制作出良好的对抗样本，而目标 HopSkipJumpAttack 需要 $10,000-20,000$ 次查询。

基于决策攻击下的防御机制

我们研究了各种防御机制在基于决策攻击下的鲁棒性。

a) 防御机制： 评估了三种防御机制：防御性蒸馏 (defensive distillation)、基于区域的分类 (region-based classification) 和对抗训练 (adversarial training)。防御性蒸馏 [33] 是梯度掩蔽 [13] 的一种形式，它训练第二个模型来预测现有相同结构模型的输出概率。我们使用 Carlini 和 Wagner [6] 提供的防御性蒸馏实现。第二种防御，基于区域的分类，属于一个广泛的机制家族，它们在输入或模型中添加测试时随机性，导致梯度被随机化 [34]。已经提出了多种变体来随机化梯度 [35, 36, 37, 38, 39]。我们采用 Cao 和 Gong [35] 中的实现，并使用建议的噪声水平。给定一个训练好的基础模型，基于区域的分类从以输入图像为中心的超立方体中采样点，使用基础模型预测每个采样点的标签，然后通过多数投票输出标签。对抗训练 [2, 3, 7, 17] 被认为是防御对抗扰动 [40, 34] 最有效的机制之一。我们评估了一个通过 Madry 等人 [7] 提出的鲁棒优化方法训练的公开可用模型。我们还在附录 C 中通过输入二值化后接随机森林构建了一个不可微模型来进一步评估我们的攻击方法。评估在 MNIST 上进行，因为在 MNIST 上防御机制（如对抗训练）效果最好。

b) 基线： 我们将我们的算法与需要访问梯度的最先进攻击算法进行比较，包括用于最小化 ${\ell }_2$-距离的 C&W 攻击 [6]、DeepFool [4]，以及用于最小化 ${\ell }_{\infty }$-距离的 FGSM [2] 和 BIM [7, 41]。对于基于区域的分类，基础分类器的梯度是相对于原始输入计算的。

我们进一步包括了专门为受威胁的防御机制设计的方法。对于防御性蒸馏，我们包括了针对 ${\ell }_{\infty }$ 优化的 C&W 攻击 [6]。对于基于区域的分类，我们包括了反向传递可微近似 (Backward Pass Differentiable Approximation, BPDA) [34]，它在 C&W 攻击和 BIM 中计算模型在随机化输入处的梯度，以代替原始输入处的梯度。所有这些方法

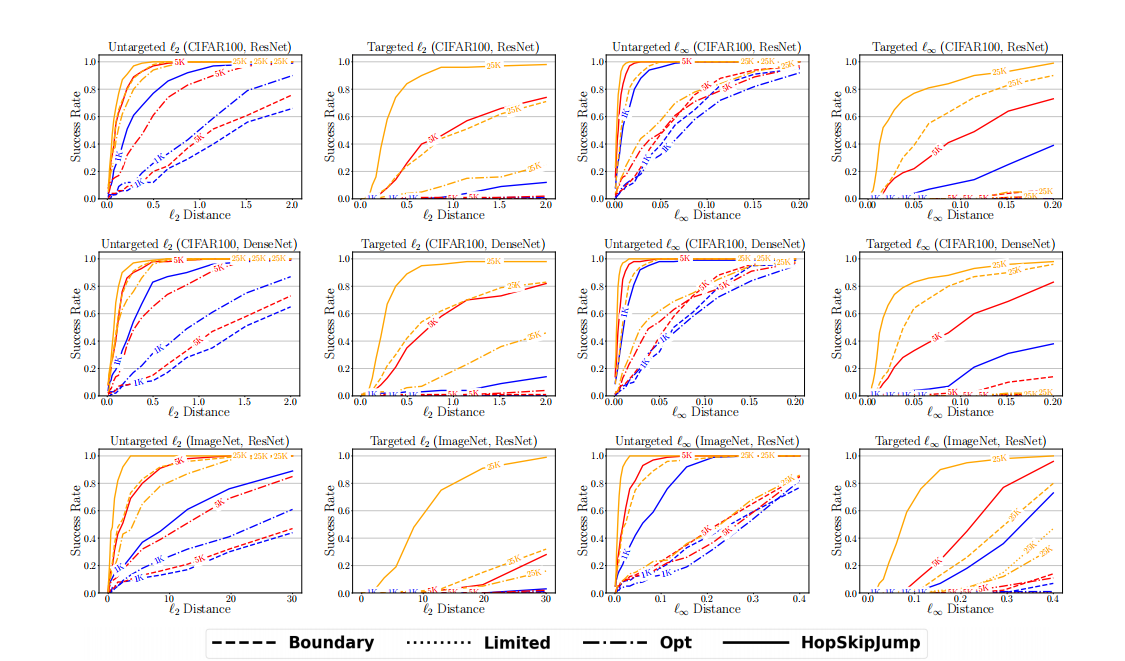
图 6：成功率与距离阈值的关系图，从上到下依次为：CIFAR-100 (ResNet)、CIFAR-100 (DenseNet)、ImageNet (ResNet)。第 1 列：非目标 ${\ell }_2$。第 2 列：目标 ${\ell }_2$。第 3 列：非目标 ${\ell }_{\infty }$。第 4 列：目标 ${\ell }_{\infty }$。

都假设可以访问模型细节甚至防御机制，这比基于决策攻击所需的条件更强的威胁模型。我们也包括了边界攻击作为基于决策的基线。

对于 HopSkipJumpAttack 和边界攻击，我们包含了三种不同查询预算规模（2K、10K 和 50K）下的成功率，以便在有限查询和足够查询下评估我们的方法。我们发现 HopSkipJumpAttack 在基于区域的分类上的收敛变得不稳定，这是由于在边界附近不确定性增加时，二分搜索步骤定位边界困难所致。因此，我们将二分搜索阈值增加到 0.01 来解决这个问题。

结果： 图 8 显示了三种防御机制下，各种攻击在不同距离阈值下的成功率。在所有三种防御上，HopSkipJumpAttack 在足够的模型查询下，表现出与最先进的白盒攻击相当或更优的性能。即使只有 1K-2K 次模型查询，它也取得了可接受的性能，尽管比最好的白盒攻击差一些。在足够的查询下，边界攻击在 ${\ell }_2$-距离度量下取得了可比的性能。但当查询次数限制在 $1,000$ 次时，它无法生成任何对抗样本。我们认为这是因为当决策边界附近存在不确定性或非平滑性时，我们批量梯度方向估计相对于边界攻击中随机游走步骤的优势变得更加明显。我们还观察到边界攻击在优化对抗样本的 ${\ell }_{\infty }$-距离度量方面不起作用，这使得评估为 ${\ell }_{\infty }$ 距离设计的防御（如 Madry 等人 [7] 提出的对抗训练）变得困难。

在蒸馏模型上，当 ${\ell }_{\infty }$-距离阈值设为 $0.3$（这是 Madry 等人 [7] 提出的用于衡量对抗鲁棒性的扰动大小）时，HopSkipJumpAttack 在 1K 和 50K 次查询下分别实现了 $86\%$ 和$99\%$ 的成功率。在 ${\ell }_2$-距离为 3.0 时，使用 2K 次查询的成功率为$91\%$。HopSkipJumpAttack 在 10K-50K 次查询下，在两种距离度量上都与 C&W 攻击取得了相当的性能。此外，防御性蒸馏的梯度掩蔽 [13] 对 HopSkipJumpAttack 的查询效率没有太大影响，表明梯度方向估计在模型对某些白盒攻击没有有用梯度的设置下是鲁棒的。

在基于区域的分类上，使用 2K 次查询，HopSkipJumpAttack 在相同的 ${\ell }_{\infty }$- 和${\ell }_2$-距离阈值下分别实现了 $82\%$ 和 $93\%$ 的成功率。使用 10K-50K 次查询，它能够达到与 BPDA（一种针对此类防御机制量身定制的白盒攻击）相当的性能。另一方面，我们观察到 HopSkipJumpAttack 在基于区域的分类上的收敛速度略慢于其在普通模型上的收敛速度，这是因为边界附近的随机性可能阻碍 HopSkipJumpAttack 中的二分搜索准确定位边界。

在对抗训练的模型上，当 ${\ell }_{\infty }$-距离阈值设为 $0.3$ 时，HopSkipJumpAttack 使用 50K 次查询实现了 $11.0\%$ 的成功率。作为比较，BIM

图 7：HopSkipJumpAttack 在 CIFAR-10 和 ImageNet 上随机选择的图像上优化 ${\ell }_2$ 距离的可视化轨迹。第 1 列：初始化（与原始图像混合后）。第 2-9 列：在 100, 200, 500, 1K, 2K, 5K, 10K, 25K 次模型查询时的图像。第 10 列：原始图像。

在给定的距离阈值下取得了 $7.4\%$ 的成功率。${\ell }_{\infty }$-HopSkipJumpAttack 的成功率转化为对抗扰动数据上 $87.58\%$ 的准确率，接近白盒攻击实现的最先进性能³。使用 1K 次查询，HopSkipJumpAttack 也取得了与 BIM 和 C&W 攻击相当的性能。

³ 参见 https://github.com/MadryLab/mnist_challenge.

VI 讨论

我们提出了一族基于新颖梯度方向估计的查询高效算法，HopSkipJumpAttack，用于基于决策的对抗样本生成，它能够优化 ${\ell }_2$ 和 ${\ell }_{\infty }$ 距离，适用于目标和非目标攻击。在可以访问梯度的前提下，我们进行了收敛性分析。我们还分析了我们蒙特卡洛梯度方向估计的误差来源，这些误差来自三个方面：非零扰动大小在边界处的偏差、偏离边界的偏差以及方差。理论分析为选择步长和扰动大小提供了见解，从而产生了一个无超参数的算法。我们还进行了广泛的实验，表明 HopSkipJumpAttack 在查询效率上优于边界攻击，并且在几种防御机制上取得了有竞争力的性能。

鉴于 HopSkipJumpAttack 能够在现实的查询预算内制作出人眼无法区分的对抗样本，社区考虑基于决策威胁模型的现实影响变得非常重要。我们还证明了 HopSkipJumpAttack 在几种防御机制上，在弱得多的威胁模型下，能够达到甚至优于最先进的白盒攻击的性能。特别是，掩蔽梯度、随机梯度和不可微性并不是我们算法的障碍。由于其有效性、高效性和对不可微模型的适用性，我们建议未来关于对抗防御的研究可以将针对 HopSkipJumpAttack 的评估作为第一步。

所有现有基于决策的算法（包括 HopSkipJumpAttack）的一个局限性是，它们需要在边界附近评估目标模型。通过限制边界附近的查询，或者通过为低置信度的输入插入额外的“未知”类别来拓宽决策边界，它们可能无法有效工作。我们还观察到，对于 HopSkipJumpAttack 在 ImageNet（其图像尺寸相对较大）上制作具有目标类别且难以察觉的对抗样本，仍然需要数万次模型查询。未来的工作可能会寻求将 HopSkipJumpAttack 与基于迁移的攻击相结合来解决这些问题。

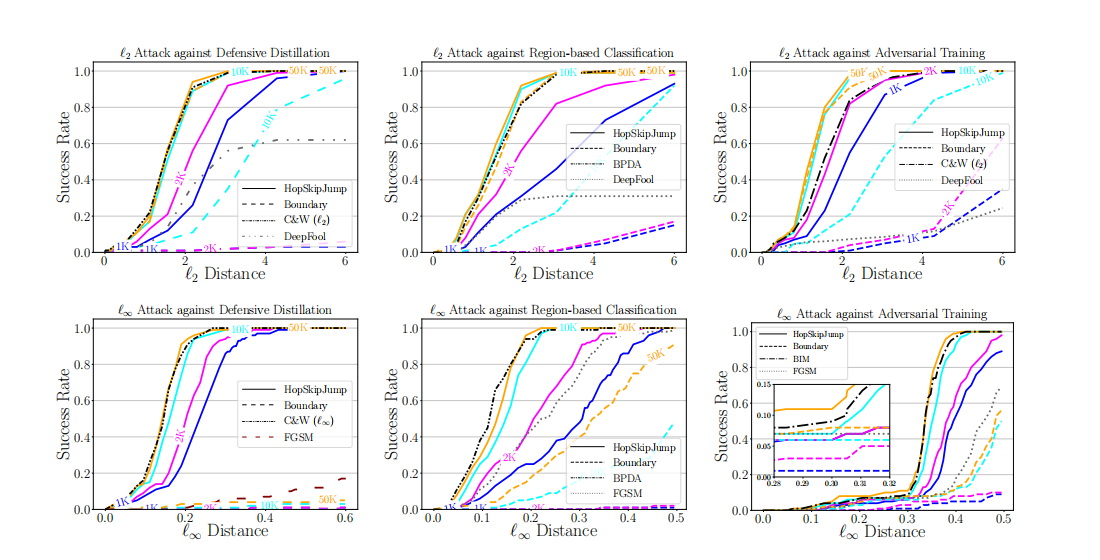
图 8：在 MNIST 上，针对蒸馏模型、基于区域分类器和对抗训练模型的成功率与距离阈值的关系图。蓝线、品红线、青线和橙线分别代表 HopSkipJumpAttack 和边界攻击在 1K、2K、10K 和 50K 次预算下的结果。不同的攻击用不同的线型绘制。在对抗训练的临界 ${\ell }_{\infty }$-距离 $0.3$ 附近包含了一个放大图。

参考文献

• [1] Christian Szegedy, Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan, Ian Goodfellow, and Rob Fergus. Intriguing properties of neural networks. In International Conference on Learning Representations, 2014. (神经网络的有趣特性)
• [2] Ian J Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. In Proceedings of the International Conference on Learning Representations, 2015. (解释和利用对抗样本)
• [3] Alexey Kurakin, Ian Goodfellow, and Samy Bengio. Adversarial machine learning at scale. In International Conference on Learning Representations, 2017. (大规模对抗机器学习)
• [4] Seyed-Mohsen Moosavi-Dezfooli, Alhussein Fawzi, and Pascal Frossard. Deepfool: a simple and accurate method to fool deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2574-2582, 2016. (Deepfool: 一种愚弄深度神经网络的简单准确方法)
• [5] Nicolas Papernot, Patrick McDaniel, Somesh Jha, Matt Fredrikson, Z Berkay Celik, and Ananthram Swami. The limitations of deep learning in adversarial settings. In 2016 IEEE European Symposium on Security and Privacy, pages 372-387. IEEE, 2016. (深度学习在对抗环境中的局限性)
• [6] Nicholas Carlini and David Wagner. Towards evaluating the robustness of neural networks. In 2017 IEEE Symposium on Security and Privacy, pages 39-57. IEEE, 2017. (评估神经网络的鲁棒性)
• [7] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, and Adrian Vladu. Towards deep learning models resistant to adversarial attacks. In International Conference on Learning Representations, 2018. (构建抵抗对抗攻击的深度学习模型)
• [8] Pin-Yu Chen, Huan Zhang, Tash Sharma, Jinfeng Yi, and Cho-Jui Hsieh. Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, pages 15-26. ACM, 2017. (Zoo: 基于零阶优化的黑盒攻击深度神经网络，无需训练替代模型)
• [9] Andrew Ilyas, Logan Engstrom, Anish Athalye, and Jessy Lin. Black-box adversarial attacks with limited queries and information. In International Conference on Machine Learning, pages 2142-2151, 2018. (有限查询和信息的黑盒对抗攻击)
• [10] Andrew Ilyas, Logan Engstrom, and Aleksander Madry. Prior convictions: Black-box adversarial attacks with bandits and priors. In International Conference on Learning Representations, 2019. (先验信念：使用 Bandits 和先验的黑盒对抗攻击)
• [11] Yanpei Liu, Xinyun Chen, Chang Liu, and Dawn Song. Delving into transferable adversarial examples and black-box attacks. In Proceedings of the International Conference on Learning Representations, 2017. (探索可迁移对抗样本和黑盒攻击)
• [12] Nicolas Papernot, Patrick McDaniel, and Ian Goodfellow. Transferability in machine learning: from phenomena to black-box attacks using adversarial samples. arXiv preprint arXiv:1605.07277, 2016. (机器学习中的可迁移性：从现象到使用对抗样本的黑盒攻击)
• [13] Nicolas Papernot, Patrick McDaniel, Ian Goodfellow, Somesh Jha, Z Berkay Celik, and Ananthram Swami. Practical black-box attacks against machine learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, pages 506-519. ACM, 2017. (针对机器学习的实用黑盒攻击)
• [14] Wieland Brendel, Jonas Rauber, and Matthias Bethge. Decision-based adversarial attacks: Reliable attacks against black-box machine learning models. In International Conference on Learning Representations, 2018. (基于决策的对抗攻击：针对黑盒机器学习模型的可靠攻击)
• [15] Thomas Brunner, Frederik Diehl, Michael Truong Le, and Alois Knoll. Guessing smart: Biased sampling for efficient black-box adversarial attacks. arXiv preprint arXiv:1812.09803, 2018. (聪明猜测：用于高效黑盒对抗攻击的有偏采样)
• [16] Minhao Cheng, Thong Le, Pin-Yu Chen, Huan Zhang, Jinf Feng Yi, and Cho-Jui Hsieh. Query-efficient hard-label black-box attack: An optimization-based approach. In International Conference on Learning Representations, 2019. (查询高效的硬标签黑盒攻击：一种基于优化的方法)
• [17] Florian Tramer, Alexey Kurakin, Nicolas Papernot, Ian Goodfellow, Dan Boneh, and Patrick McDaniel. Ensemble adversarial training: Attacks and defenses. In International Conference on Learning Representations, 2018. (集成对抗训练：攻击与防御)
• [18] Abraham D Flaxman, Adam Tauman Kalai, and H Brendan McMahan. Online convex optimization in the bandit setting: gradient descent without a gradient. In Proceedings of the Sixteenth Annual ACM-SIAM Symposium on Discrete Algorithms, pages 385-394. SIAM, 2005. (Bandit 设置下的在线凸优化：无梯度的梯度下降)
• [19] Alekh Agarwal, Dean P Foster, Daniel J Hsu, Sham M Kakade, and Alexander Rakhlin. Stochastic convex optimization with bandit feedback. In Advances in Neural Information Processing Systems, pages 1035-1043, 2011. (具有 Bandit 反馈的随机凸优化)
• [20] Yurii Nesterov and Vladimir Spokoiny. Random gradient-free minimization of convex functions. Foundations of Computational Mathematics, 17(2):527-566, 2017. (凸函数的随机无梯度最小化)
• [21] John C Duchi, Michael I Jordan, Martin J Wainwright, and Andre Wibisono. Optimal rates for zero-order convex optimization: The power of two function evaluations. IEEE Transactions on Information Theory, 61(5):2788-2806, 2015. (零阶凸优化的最优速率：两次函数评估的力量)
• [22] Sijia Liu, Bhavya Kalikhura, Pin-Yu Chen, Paishun Ting, Shiyu Chang, and Lisa Amini. Zeroth-order stochastic variance reduction for nonconvex optimization. In Advances in Neural Information Processing Systems, pages 3731-3741, 2018. (非凸优化的零阶随机方差缩减)
• [23] David Kincaid, David Ronald Kincaid, and Elliott Ward Cheney. Numerical Analysis: Mathematics of Scientific Computing, volume 2. American Mathematical Soc., 2009. (数值分析：科学计算的数学)
• [24] Michel Ledoux. The Concentration of Measure Phenomenon. Number 89. American Mathematical Soc., 2001. (测度集中现象)
• [25] Nicolas Papernot, Fartash Faghri, Nicholas Carlini, Ian Goodfellow, Reuben Feinman, Alexey Kurakin, Chiang Xie, Yash Sharma, Tom Brown, Aurko Roy, Alexander Matyasko, Vahid Behzadan, Karen Hambardzumyan, Zhishuai Zhang, Yi-Lin Juang, Zhi Li, Ryan Sheatsley, Abhibhav Garg, Jonathan Uesato, Will Gierke, Yinpeng Dong, David Berthelot, Paul Hendricks, James Rauber, and Rujun Long. Technical report on the cleverhaus v2.1.0 adversarial examples library. arXiv preprint arXiv:1610.00768, 2018. (CleverHans v2.1.0 对抗样本库技术报告)
• [26] Jonas Rauber, Wieland Brendel, and Matthias Bethge. Foolbox: A python toolbox to benchmark the robustness of machine learning models. arXiv preprint arXiv:1707.04131, 2017. (Foolbox: 一个用于基准测试机器学习模型鲁棒性的 Python 工具箱)
• [27] Alex Krizhevsky. Learning multiple layers of features from tiny images. Technical report, Citeseer, 2009. (从微小图像中学习多层特征)
• [28] J. Deng, W. Dong, R. Socher, L.-J. Li, K. Li, and L. Fei-Fei. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2009. (ImageNet: 一个大规模分层图像数据库)
• [29] Francois Chollet et al. Keras. https://keras.io, 2015.
• [30] Jan Hendrik Metzen, Tim Genewein, Volker Fischer, and Bastian Bischoff. On detecting adversarial perturbations. In International Conference on Learning Representations, 2017. (论检测对抗扰动)
• [31] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Identity mappings in deep residual networks. In European Conference on Computer Vision, pages 630-645. Springer, 2016. (深度残差网络中的恒等映射)
• [32] Gao Huang, Zhuang Liu, Laurens Van Der Maaten, and Kilian Q Weinberger. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4700-4708, 2017. (密集连接卷积网络)
• [33] Nicolas Papernot, Patrick McDaniel, Xi Wu, Somesh Jha, and Ananthram Swami. Distillation as a defense to adversarial perturbations against deep neural networks. In 2016 IEEE Symposium on Security and Privacy, pages 582-597. IEEE, 2016. (蒸馏作为防御深度神经网络对抗扰动的防御手段)
• [34] Anish Athalye, Nicholas Carlini, and David Wagner. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. In International Conference on Machine Learning, pages 274-283, 2018. (混淆的梯度带来虚假的安全感：规避对抗样本的防御)
• [35] Xiaoyu Cao and Neil Zhenqiang Gong. Mitigating evasion attacks to deep neural networks via region-based classification. In Proceedings of the 33rd Annual Computer Security Applications Conference, pages 278-287. ACM, 2017. (通过基于区域的分类减轻对深度神经网络的规避攻击)
• [36] Xuanqing Liu, Minhao Cheng, Huan Zhang, and Cho-Jui Hsieh. Towards robust neural networks via random self-ensemble. In Proceedings of the European Conference on Computer Vision (ECCV), pages 369-385, 2018. (通过随机自集成构建鲁棒神经网络)
• [37] Guneet S. Dhillon, Kamyar Azizzadenesheli, Jeremy D. Bernstein, Jean Kossaifi, Aran Khanna, Zachary C. Lipton, and Animashree Anandkumar. Stochastic activation pruning for robust adversarial defense. In International Conference on Learning Representations, 2018. (用于鲁棒对抗防御的随机激活剪枝)
• [38] Jeremy Cohen, Elan Rosenfeld, and Zico Kolter. Certified adversarial robustness via randomized smoothing. In International Conference on Machine Learning, pages 1310-1320, 2019. (通过随机平滑获得经认证的对抗鲁棒性)
• [39] Cihang Xie, Jianyu Wang, Zhishuai Zhang, Zhou Ren, and Alan Yuille. Mitigating adversarial effects through randomization. In International Conference on Learning Representations, 2018. (通过随机化减轻对抗效应)
• [40] Nicholas Carlini and David Wagner. Adversarial examples are not easily detected: Bypassing ten detection methods. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, pages 3-14. ACM, 2017. (对抗样本不易被检测：绕过十种检测方法)
• [41] Alexey Kurakin, Ian J Goodfellow, and Samy Bengio. Adversarial examples in the physical world. In Artificial Intelligence Safety and Security, pages 99-112. Chapman and Hall/CRC, 2018. (物理世界中的对抗样本)
• [42] F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot, and E. Duchesnay. Scikit-learn: Machine learning in Python. Journal of Machine Learning Research, 12:2825-2830, 2011. (Scikit-learn: Python 中的机器学习)