【论文阅读69】-DeepHGNN复杂分层结构下的预测

这篇论文提出的 DeepHGNN 框架，把层级时间序列预测问题转化为图学习问题，通过 图神经网络 + 层级插值 + 端到端一致性 来提升预测精度和层级一致性，在实验中优于现有方法。

1. 研究背景

• 层级时间序列（Hierarchical Time Series, HTS） 在很多实际场景中出现（如销售预测：公司 → 区域 → 门店 → 产品），其特点是多个时间序列之间存在层次结构。
• 挑战在于：需要既保证各层级预测的一致性（coherence），又提升整体预测精度。
• 传统方法往往先独立预测，再通过“自上而下”或“自下而上”的方式做 预测调整（reconciliation），但这样可能丢失层级间共享的信息。

2. 主要贡献

论文提出了 DeepHGNN 框架，这是一个结合 图神经网络（Graph Neural Networks, GNN） 的新型层级预测方法。

1. 图表示层级结构

   • 将层级时间序列建模为一个图（节点代表时间序列，边代表层级关系）。
   • 通过 图卷积 学习跨层级和序列之间的依赖关系。

2. 层级插值机制（Hierarchical Interpolation）

   • 利用图结构在不同层级间传播信息，显式共享信号。
   • 解决了不同层级预测能力差异的问题（上层序列通常更平稳、易预测；底层更噪声化）。

3. 端到端一致性机制（End-to-End Reconciliation）

   • 在预测过程中就保证了不同层级预测的一致性，而不是事后再做修正。
   • 避免了传统 reconciliation 的额外误差。

4. 充分利用层级信息

   • 上层预测相对稳定，可以为下层预测提供先验约束。
   • 下层的细粒度信息反过来提升整体的准确性。

5. 实验与结论

• 在多个数据集上与 最新的层级预测模型 对比，DeepHGNN 显示出 更高的预测精度 和 层级一致性。
• 证明了 GNN 在处理 多变量、层级化时间序列预测 中的优势。

[1] Sriramulu A, Fourrier N, Bergmeir C. DeepHGNN: study of graph neural network based forecasting methods for hierarchically related multivariate time series[J]. Expert Systems with Applications, 2025, 282: 127658.

作者及单位

• Abishek Sriramulu

  • Department of Data Science & Artificial Intelligence, Monash University, Clayton VIC 3800, Australia
  • Tymestack, Melbourne, Australia

• Nicolas Fourrier

  • Tymestack, Melbourne, Australia
  • Léonard de Vinci Pôle Universitaire, Research Center, 92 916 Paris La Défense, France

• Christoph Bergmeir （通讯作者）

  • Department of Data Science & Artificial Intelligence, Monash University, Clayton VIC 3800, Australia
  • Department of Computer Science and Artificial Intelligence, University of Granada, Spain
    

摘要
图神经网络（GNN）在预测领域已获得广泛关注，尤其在能够同时捕捉序列内的时间相关性与序列间的相互关系方面展现了独特优势。本文提出了一种新颖的分层图神经网络（DeepHGNN）框架，专门用于复杂分层结构下的预测。DeepHGNN 的独特之处在于其创新性的基于图的分层插值方法和端到端的对账机制。该方法不仅保证了不同分层层级上的预测精度与一致性，同时实现了跨层级信号的共享，从而解决了分层预测中的关键挑战。

在分层时间序列中，一个关键洞察是不同层级的可预测性存在差异，高层级通常表现出更易预测的成分。DeepHGNN 充分利用这一洞察，通过汇聚并利用所有层级的知识，从而提升整体预测精度。我们在多个先进模型上的全面评估结果表明，DeepHGNN 具有显著的性能优势。本研究不仅验证了 DeepHGNN 在显著提升预测精度方面的有效性，同时也对图方法在分层时间序列预测中的应用提供了新的理解。
关键词：分层预测；图神经网络；时间序列

• 收稿日期：2024年11月13日
• 修订日期：2025年3月27日
• 接收日期：2025年4月8日
• 在线发布日期：2025年4月17日
• 期刊：Expert Systems With Applications, 卷 282 (2025), 文章编号 127658

1. 引言

分层预测（Hierarchical forecasting）是一种在不同层级上进行预测的方法。该方法考虑层级之间的相互关系与依赖性，从而确保各层级的预测结果与更高层级保持一致。举例来说，假设某零售连锁在全国不同城市设有门店。我们可以对每个门店中某一产品的需求进行预测，然后将这些预测值汇总以获得城市层面的区域预测，再进一步汇总得到整个组织的全国预测。分层预测不仅能够为组织不同部分的绩效提供有价值的洞察，还能促进更优的决策制定。同时，它在库存规划与管理、供应链管理以及财务预算方面也具有帮助。

分层预测的关键挑战在于预测结果必须在层级结构中保持一致性。这意味着较低层级的预测之和应等于较高层级的预测。例如，一个区域内所有门店需求预测的总和应与该区域整体的需求预测保持一致。

目前，大多数先进的分层预测方法通常采用两步流程：

1. 预测步骤：为层级中的全部或部分时间序列生成单独的预测。
2. 对账步骤：确保跨层级的预测结果保持一致性。

实现分层预测一致性的一种常见方法是自上而下法（top-down approach）。该方法首先在层级最高层生成预测，然后通过拆分高层预测来获得低层预测（Nenova & May, 2016）。这种方法易于实现，并且在高层预测时较为有用。然而，由于其依赖拆分，高层预测生成的低层结果往往不如直接方法准确。

另一种方法是自下而上法（bottom-up approach），即先为低层生成预测，再汇总得到高层预测（Nenova & May, 2016）。当预测重点在低层级时，这种方法更为适用。

近年来，最优对账方法（optimal reconciliation approaches）（Hyndman, Ahmed, Athanasopoulos, & Shang, 2011）逐渐流行。该方法通过优化一个对账函数来确保不同层级的预测保持一致。该函数可以建模为线性或非线性优化问题，并可采用线性规划或二次规划等方法求解。事实证明，最优对账方法能够有效提升分层预测的精度。其基本流程是：先为层级中所有时间序列生成预测，再通过对账过程实现预测一致性（Hyndman et al., 2011）。

不过，这些方法往往建立在强假设之上，例如预测模型无偏、残差联合协方差平稳等。此外，它们对层级中时间序列数量快速增长的情况缺乏可扩展性（Wickramasuriya, Athanasopoulos, & Hyndman, 2019）。而且在大规模数据集上，这些方法表现不佳，因为高度分解后的数据通常具有较低的信噪比。

近年来，图神经网络（GNN） 已被证明能够有效建模序列间关系与序列内模式（Feng et al., 2024; Gao, Zhang, Zhang, & Li, 2023; Guo et al., 2023; Shin & Yoon, 2023; Xie et al., 2019）。在分层预测中，GNN 尤其具有潜力，因为目标是预测多个存在分层结构的相关时间序列，例如不同产品与地区的销售数据。GNN 是一种专为处理图结构数据而设计的神经网络，因此非常适合建模分层结构中不同时间序列间的关系。

在分层预测问题中，时间序列可以按照其层级组织为一棵树或有向无环图（DAG）。其中，图的节点代表时间序列，边则表示层级关系。通过在图上传播信息，GNN 可以捕捉这些层级关系，使模型在预测单个时间序列时能够利用层级中相关序列的信息。例如，模型可以学习如何将来自高层（如区域销售数据）的信息传播到低层（如具体门店的销售数据），从而提升预测精度。

总体而言，GNN 为分层预测中复杂时间序列关系建模提供了一种强有力的工具，这不仅能带来更准确的预测结果，也能帮助决策者做出更合理的判断。

在此基础上，我们的研究提出了以下若干创新性贡献：

• 提出了一种分层图神经网络（DeepHGNN） 框架，利用分层结构提升各层级预测精度，并引入端到端对账机制；
• 推动了基于图的方法在分层时间序列预测中的发展，展示了分层结构与图数据表示的有效结合；
• 通过全面评估验证，证明了 GNN 在预测精度上优于多种先进模型，并在该领域建立了新的基准。

2. 相关工作

本节讨论图神经网络（GNN）和分层预测领域的相关研究。

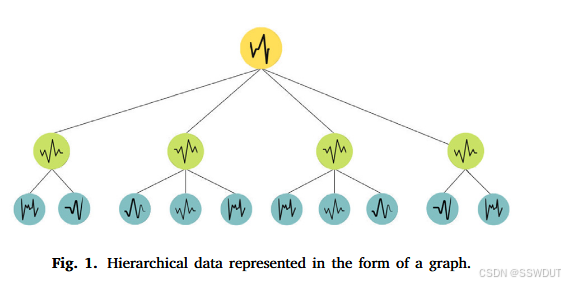
图 1：以图结构形式表示的分层数据。

2.1. 基于 GNN 的多变量时间序列预测

GNN 在多变量时间序列预测中展现出广阔前景，因为它们能够捕捉变量之间复杂的依赖关系。GNN 是一种作用于图结构上的神经网络，图是一类数学对象，用于表示实体之间的关系。在多变量时间序列预测的背景下，实体可以是不同的变量，而关系则表示它们随时间的依赖性。

如图 1 所示，在图结构中，每个节点对应一个单独的时间序列，连接它们的边表示序列之间的关系。传统预测方法往往依赖线性或简单非线性关系来建模变量间依赖，这在处理更复杂关系时可能力不从心。相比之下，GNN 通过利用数据的整体图结构来克服这一局限，从而学习复杂依赖关系。

图是定义对象或实体间依赖关系的数据结构。在图中，每个对象或实体由一个节点表示，它们之间的依赖关系由边表示。假设图中节点总数为 $n$，则图结构可通过邻接矩阵 $\mathbf{A}\in {\mathbb{R}}^{n\times n}$ 来表示：若节点 $v\_i$ 与 $v\_j$ 之间存在边，则 KaTeX parse error: Undefined control sequence: \[ at position 2: A\̲[̲i,j] > 0；若不存在边，则 KaTeX parse error: Undefined control sequence: \[ at position 2: A\̲[̲i,j] = 0。邻接矩阵由此刻画了图中节点间的依赖关系。

GNN 的核心思想是消息传递机制（message-passing system）：每个节点从其邻居聚合信息，处理后再传递给邻居。该过程重复进行，直到达到稳定状态。最终的输出是通过对全图中所有节点的信息进行聚合得到的。

常见的 GNN 架构包括图卷积网络（GCN）与图注意力网络（GAT）。GCN 通过卷积操作将邻居节点特征组合生成新的节点特征，类似于传统 CNN 在图像数据上的操作。GAT 则引入注意力机制，为图中不同节点与边分配权重，从而在建模复杂关系时更灵活。

GNN 的一个主要优势在于能捕捉变量间的复杂依赖关系。随着该研究方向的不断发展，GNN 在时间序列预测任务中的应用将越来越普及并展现更高效能。近年来，为了建模复杂的时空依赖，已经提出了多种基于 GNN 的方法，包括：

• DCRNN（Li et al., 2018）：结合图卷积与循环神经网络的编码–解码架构；
• MTGNN（Wu et al., 2020）：集成图卷积与膨胀时间卷积模块；
• ADLGNN（Sriramulu, Fourrier, & Bergmeir, 2023）：引入自适应依赖学习注意力机制；
• MTGODE（Liu, Shojaee, & Reddy, 2023）：利用时空常微分方程建模动态演化；
• ASTGCN（Bai et al., 2021）：结合 GRU、图卷积与注意力机制；
• SpecTGNN（Jin et al., 2023）：证明了谱–时域 GNN 可作为通用逼近器。

这些方法通过结合图操作、注意力机制、时间卷积与神经常微分方程，有效地利用了空间相关性、长短期时间模式及动态演化特征。

2.1.1. DCRNN

Li 等（2018）提出了一种基于图扩散卷积的循环神经网络（DCRNN），主要用于交通预测。该模型基于 LSTM，但有以下关键区别：

1. 使用 CNN 从时间序列中提取特征，从而学习长程依赖，这对预测至关重要；
2. 使用 RNN 来建模数据的时间动态，从而学习数据随时间的演变模式。

DCRNN 的目标是：给定历史观测 $X(t-T^{\prime }),\dots ,X\_t$，预测未来 $X(t+1),\dots ,X(t+T)$，其中 $X$ 来自网络中 $N$ 个传感器。网络被建模为加权有向图 $G=(V,E,W)$，其中：

• $V$ 表示节点集合（传感器），
• $E$ 表示边集合，
• $W$ 是加权邻接矩阵，编码基于网络距离的邻近性。

空间依赖通过图上的扩散过程来建模，该过程被定义为带有重启概率 $\alpha$ 的随机游走。其平稳分布 $\mathbf{P}$ 刻画了节点间的相关性：

$$P=\sum _{k=0}^{\infty }\alpha (1-\alpha {)}^k(D^{-1}W{)}^k$$
其中，$D^{-1}$ 是节点的对角出度矩阵，$k$ 表示扩散步数。基于此，提出了一种扩散卷积：

$$X{\star }_G{f}_{\theta }=\sum _{k=0}^{K-1}{\theta }_{k,1}(D^{-1}W{)}^{k}X+{\theta }_{k,2}(D^{-1}{W}^{\top }{)}^{k}X$$
其中，$\theta \in {\mathbb{R}}^{K\times 2}$ 是滤波器参数。该操作捕捉了图上扩散的局部模式，类似于常规卷积。DCRNN 用扩散卷积替代了 GRU 中的矩阵乘法，从而能更好建模时空相关性。

此外，DCRNN 采用编码–解码结构与scheduled sampling 进行多步预测：编码器处理历史序列，解码器则基于编码器状态递归生成预测。训练时通过最大化未来序列的似然函数并使用反向传播进行优化。

2.1.2. MTGNN

Wu 等（2020）提出了 MTGNN，一种结合图神经网络与膨胀时间卷积的预测模型，主要模块包括：

• 图卷积模块：

  • 通过新颖的混合跳数传播层（mix-hop propagation layer）利用学习得到的邻接矩阵建模空间依赖；
  • 该层通过信息传播与信息选择两个步骤实现：

  信息传播：

  $$H^{(k)}=\beta H_{\text{in}}+(1-\beta )\tilde{A}{H}^{(k-1)}$$
  其中，$\tilde{A}={\tilde{D}}^{-1}(A+I)$，$\tilde{D}\ast ii=1+\sum \_jA\ast ij$。

  信息选择：

  $$H_{\text{out}}=\sum _{k=0}^K{H}^{(k)}{W}^{(k)}$$
  其中，$W^{(k)}$ 为可学习参数。

  混合跳数传播避免了过平滑问题，同时保留了局部性特征。

• 时间卷积模块：

  • 使用多尺度膨胀卷积捕捉时间模式；
  • 采用并行 dilated inception 层（卷积核大小为 2、3、6、7）提取多尺度特征；
  • 通过指数扩张的膨胀率增加感受野，以建模长短期依赖。

• 学习算法：

  • 子图训练：每次迭代随机划分节点组，减少内存与计算复杂度；
  • 课程学习：逐步增加预测步数，从 1 步到 $Q$ 步，避免短期预测主导优化。

该模型将空间与时间模块集成到端到端架构中。但其主要缺点是：当变量之间存在双向因果关系时，预测结果可能并非最优。

2.1.3. ADLGNN

Sriramulu 等人（2023）提出了一种方法，通过统计手段识别信息量更高的邻居节点，并结合注意力机制，从而减少邻居数量并避免负迁移学习，以降低大型 GNN 模型的运行复杂度。

ADLGNN 架构包含两个主要组件：

• GNN 模块：用于学习单个时间序列的内部依赖；
• 自适应依赖学习模块：用于学习不同时间序列之间的依赖关系。

该自适应依赖学习模块基于图注意力网络（GAT）机制，用于学习多变量时间序列数据中各时间序列之间的注意力权重。注意力权重用于衡量不同时间序列对目标时间序列下一时刻预测的重要性。
此外，采用了一种改进的时空注意力机制来捕捉时空模式。该机制通过因果卷积生成查询（$q$）、键（$k$）、值（$v$），并在空间与时间维度上同时执行注意力操作，形式类似于标准自注意力机制：

$$\text{Attention}(q,k,v)=\text{softmax}\left(\frac{q{k}^{\top }}{\sqrt{d_k}}\right)v$$
其中 $q,k,v$ 由输入经过卷积得到。注意力分数最终通过跳跃连接传递到输出模块。

2.1.4. MTGODE

Jin 等人（2022）提出了一种神经图常微分方程（Graph ODE） 方法，将空间与时间消息传递统一起来，实现更深层的图传播与更细粒度的时间信息聚合。该方法引入动态图神经 ODE，用于捕捉多变量时间序列中的复杂时序依赖关系。

具体来说，ODE 用于建模图随时间的演化，而 GNN 用于学习图中节点间的关系。该模型包含两个 ODE：

• 空间 ODE：沿学习得到的图传播信息，建模空间依赖：

  $$\frac{d{H}_G(t)}{dt}=(\hat{A}-I_N)H_G(t)$$
  其中 $H\_G(t)$ 表示时刻 $t$ 的空间潜在表示，$\hat{A}$ 是归一化邻接矩阵，$I\_N$ 是单位矩阵。该连续传播机制避免了传统 GNN 的过平滑问题。

• 时间 ODE：聚合时间维度上的信息：

  $$\frac{d{H}_T(t)}{dt}=P(\text{TCN}(H_T(t),t),R)$$
  其中 $H\_T(t)$ 表示时刻 $t$ 的时间潜在表示，$\text{TCN}$ 为时间卷积模块，$P$ 为填充函数，$R$ 表示感受野大小。该设计实现了连续时间的时序建模，避免了离散模型的限制。

该方法的动态特性体现在：空间 ODE 作为时间 ODE 每一步求解过程中的内嵌步骤，从而同时建模时空依赖。

2.1.5. ASTGCN

Bai 等人（2021）提出了注意力时序图卷积网络（ASTGCN），该模型旨在同时捕捉全局时序动态与空间相关性。其架构包含三个核心组件：

1. GCN 层：用于捕捉空间依赖，公式为：

   $$H^{(l+1)}=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{\Theta }^{(l)})$$
   其中 $H^{(l)}$ 是第 $l$ 层的输出，$\tilde{A}=A+I$ 是带自连接的邻接矩阵，$\tilde{D}$ 是对应的度矩阵，${\Theta }^{(l)}$ 为权重。

2. GRU 层：用于捕捉局部时间动态：

   $$u_t=\sigma (W_u\ast [X_t,h_{t-1}]+b_u)$$
   $$r_t=\sigma (W_r\ast [X_t,h_{t-1}]+b_r)$$
   $$c_t=\tanh (W_c\ast [X_t,(r_t\odot h_{t-1})]+b_c)$$
   $$h_t=u_t\odot h_{t-1}+(1-u_t)\odot c_t$$
   其中 $u\_t,r\_t$ 为更新门与重置门，$c\_t$ 为候选记忆，$h\_t$ 为 GRU 输出。

3. 注意力机制：用于捕捉全局时序动态，通过为不同时间点分配不同权重，突出重要时间点：

   $$e_i=W^{(2)}(W^{(1)}H+b^{(1)})+b^{(2)}$$
   $${\alpha }_i=\frac{\exp (e_i)}{{\sum }_{k=1}^n\exp (e_k)}$$
   $$C_t=\sum _{i=1}^n{\alpha }_i{h}_i$$
   其中 $H=(h\_1,...,h\_n)$ 是 GRU 输出序列，$e\_i$ 为注意力得分，$\alpha \_i$ 为归一化权重，$C\_t$ 为上下文向量。

2.1.6. GRAM-ODE

Liu 等人（2023）提出了基于图的多 ODE 神经网络（GRAM-ODE），（ordinary differential equation ）用于捕捉复杂的时空模式。其框架由两条输入流（连接图与动态时间规整 DTW 图）、每个图的三条并行通道、两层 GRAM-ODE 以及一个注意力模块（AM）组成。

• GRAM-ODE 层：在两个时间卷积网络（TCN）之间嵌入一个多 ODE GNN 模块，主要功能包括：

  • 全局 / 局部 / 边消息传递；
  • 消息过滤（防止局部与全局信息发散）；
  • 门控聚合与残差更新。

  三种消息传递机制包括：

  全局消息传递：

  $$GM=H_g(0)+{\int }_0^t{f}_g(H_g(\tau ),\hat{A},T_g,W)d\tau$$
  $$f_g=H_g(t){\times }_2(\hat{A}-I)+((S(T_g)-I)H_T^g(t){)}^{\top }+H_g(t){\times }_4(W-I)$$
  局部消息传递：

  $$LM=\text{LocalMessagePassing}(ATT,H_l(0),\hat{A},T_l,W)$$
  边消息传递：

  $$EM=\text{EdgeMessagePassing}(H_e(0),\hat{A},T_e)$$
  其中 $T\_g,T\_e$ 在全局与边 ODE 中共享权重。

  最终的门控聚合：

  $$H^{\prime }=\text{Aggregation}(GM,LM,EM)=\frac{1}{2K}\sum _{m=1}^K\sum _{n\ne m}{p}_m\odot \text{softmax}(p_n)$$
  其中 $p\_m\in GM,LM,EM$。

• 时间卷积网络（TCN）：位于 ODE 模块前后，用于捕捉时间依赖。采用 1D 膨胀卷积扩展感受野：

  $$H_t^{TCN(l)}=\sigma (W_l{\ast }_{d_l}{H}_{t-1}^{TCN(l-1)})$$
  其中 $d\_l=2^{l-1}$ 表示指数膨胀率。堆叠多层 TCN 以建模长程依赖。

• 注意力模块（AM）：用于跨两条图流与多通道进行特征聚合。输入为拼接后的嵌入 $X\in {\mathbb{R}}^{B\times N\times L\times C^{\prime }}$。与传统池化不同，AM 通过数据驱动的注意力分数自适应选择最相关的特征，从而实现更具表达力的融合。

2.1.7. SpecTGNN

Jin 等人（2023）证明，在温和假设条件下，谱-时间图神经网络（SpecTGNN）可以作为多变量时间序列预测的通用逼近器。该论文提出的设计原则描述了如何利用正交基和独立谱滤波器来构建具有理论上可证明表达能力的 SpecTGNN 模型。所提出的模型 Temporal Graph GegenConv (TGC) 验证了这些理论，其在一个简单的线性架构中展现了强大的性能。

TGC 架构堆叠了多个模块，每个模块包括：

• 图卷积（基于 Gegenbauer 多项式基），
• 粗粒度与细粒度的时间频域滤波，
• 残差连接。

在图卷积部分，TGC 采用 Gegenbauer 多项式基，因为它具有快速收敛、将 Chebyshev 多项式推广到更灵活的权函数的能力，以及相较于 Jacobi 等其他正交基的简洁性。Gegenbauer 多项式递归定义如下：

$$P_k^{\alpha }(x)=\frac{1}{k}[2x(k+\alpha -1)P_{k-1}^{\alpha }(x)-(k+2\alpha -2)P_{k-2}^{\alpha }(x)]$$
其中：

$$P_0^{\alpha }(x)=1,P_1^{\alpha }(x)=2\alpha x$$
它们在区间 $[-1,1]$ 上相对于权函数 $(1-x^2{)}^{\alpha -1/2}$ 是正交的。

图卷积操作公式为：

$$g_{\theta }(\hat{L})\star X_t=\sum _{k=0}^K{\theta }_k{P}_k^{\alpha }(\hat{A})X_t$$
其中，$\hat{A}$ 为归一化邻接矩阵。

TGC 采用两种简单的时间频域滤波：

• 粗粒度：对输入执行离散傅里叶变换（DFT），选择/过滤部分分量后再进行逆 DFT；
• 细粒度：将输入分解为趋势与细节，分别过滤后再重组。

这种细粒度滤波有助于捕捉输入信号中的不同频率成分。

2.2. 分层预测

分层时间序列预测涉及预测大量具有层级结构的相关时间序列。分层结构广泛存在于多个领域，例如销售预测、需求预测和供应链管理。在这些应用中，层级最底层的个体时间序列预测会被聚合以生成更高层级的预测。
分层预测的优势在于：

1. 它能够利用层级中不同层次的信息，从而更有效地预测大规模的相关时间序列；
2. 通过整合相关时间序列的信息，它还能为个体时间序列提供更高精度的预测。

分层预测通常采用 两步法：

• 第一步：为所有层级的时间序列生成预测；
• 第二步：在一个后续的对账步骤中，调整预测结果以确保不同层级间加总的一致性（Hollyman, Petropoulos, & Tipping, 2021）。

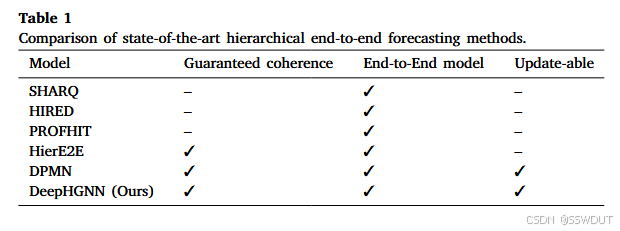
近年来，出现了 端到端系统，模型可以同时优化预测与对账，从而实现更高的预测精度。本研究关注此类端到端方法，并与 DeepHGNN 进行比较。
表 1 展示了现有端到端分层预测方法的特征。

2.2.1. SHARQ

Han, Dasgupta 和 Ghosh（2021）提出了一种方法，用于捕捉相邻聚合层级中相关序列的相互关系。该方法通过优化正则化损失函数来实现：模型为加总矩阵中的每个顶点学习权重，这一权重项作为正则化因子，强制预测在层级间保持一致性。然而，该方法并不能保证预测完全一致。

• 在层级结构中，时刻 $t$ 的节点 $v_i$ 的时间序列值记为 $x_{v_i}(t)$。
• 节点间的父子关系用有符号边 $e_{i,j}$ 表示：若 $i$ 是 $j$ 的父节点，则 $e_{i,j}=1$；若相反，则 $e_{i,j}=-1$。
• 对于每个节点 $i$，训练一个预测模型 $g_i$，输入为过去数据 $X_i$ 和参数 ${\theta }_i$，输出为未来预测值 $Y_i$。

目标函数由 数据拟合损失 和 一致性正则化项 构成：
$$L(g_i(X_i,{\theta }_i),Y_i)=\sum _{m=1}^{M}L(g_i(X_i^m,{\theta }_i),Y_i^m)$$
一致性约束通过最小化父节点预测与子节点预测和的差异来实现，其强度由正则化权重 ${\lambda }_i$ 控制：
$$L_c(g_i,Y_i,g_j)=L(g_i,Y_i)+{\lambda }_i\Vert g_i-\sum _j{e}_{i,j}{g}_j{\Vert }^2$$
通过优化该联合损失函数，模型能够在单序列预测精度与层级一致性之间取得平衡。

2.2.2. HIRED

Paria, Sen, Ahmed 和 Das（2021）提出了一种新的分层时间序列预测方法，由 时间变化自回归（TVAR）模型 和 基函数分解（BD）模型 两部分组成，能够同时预测大量分层时间序列，并利用层级树中的相关性提升精度。
预测形式：
$${\hat{y}}_t^{(i)}={\hat{y}}_{t+1}^{TVAR(i)}+{\hat{y}}_{t+1}^{BD(i)}$$

• TVAR 部分：采用带时变系数的线性自回归：

$${\hat{y}}_{t+1}^{TVAR(i)}=f(y_{t-H:t-1}^{(i)},X_{t-H:t},Z_{t-H:t})$$

其中系数共享，但会随时间和输入变化而调整。

• BD 部分：将时间序列分解为全局基函数的线性组合：

$${\hat{y}}_{t+1}^{BD(i)}={\theta }_{i}b(X_{t-H:t},Z_{t-H:t})$$
其中，基函数 $b(\cdot )$ 和权重 ${\theta }_i$ 联合学习。权重通过正则化约束以满足层级一致性。
该方法可用小批次训练，支持大规模数据。但其一致性仍无法完全保证。

2.2.3. PROFHIT

Kamarthi, Kong, Rodríguez, Zhang 和 Prakash（2022）提出了一种 概率神经网络模型，首先学习每个时间序列的预测分布，并基于此得到一个精化分布，从而同时建模个体序列与层级信息。
模型包含两个模块：

1. TSFNP 模块：将历史数据编码为潜在表示，并建模为高斯分布，输出原始预测分布。

   • PNE（概率神经编码器）：将历史编码为随机潜变量；
   • SDCG（随机数据相关图）：建模序列间相关性；
   • PDD（预测分布解码器）：输出高斯分布参数。

2. 精化模块：利用所有序列信息对预测分布进行精化，使其均值与方差更符合层级约束。

该方法使用分布一致性损失来正则化预测，使其接近由子节点加总而来的分布。尽管是端到端模型，但需要对 TSFNP 进行预训练。

2.2.4. HierE2E

Rangapuram 等人（2021）提出了一种端到端深度神经网络分层预测模型，能够保证预测一致性。

• 使用 DeepVAR（多变量预测模型）生成未来时间步的联合预测分布：

$$p(y_t;{\Theta }_t)=\mathcal{N}(y_t;{\mu }_t,{\Sigma }_t)$$

其中 ${\mu }_t,{\Sigma }_t$ 依赖于所有序列的历史滞后项。预测与一致性约束在一个端到端框架中联合优化，直接输出满足层级约束的概率预测。

2.2.5. DPMN

Olivares, Meetei, Ma, Reddy 和 Cao（2021）提出了 深度泊松混合网络（DPMN），结合神经网络与统计建模：

• 预测分布被建模为有限个泊松分布的混合，类似于使用泊松核的核密度估计；
• 通过神经网络参数化泊松率 $\lambda$，并学习混合权重；
• 利用膨胀卷积提取历史特征，再通过 MLP 解码得到泊松参数；
• 聚合层级的预测通过对泊松率求和实现：
  $${\lambda }_a=A_{ab}{\lambda }_b$$
  其中 $A$ 为聚合矩阵。该方法从结构上保证了一致性。

3. 方法设计与框架

分层图神经网络（DeepHGNN） 是一种新颖的端到端分层预测模型，旨在通过引入更多层级信息来提升分层时间序列预测的准确性。
DeepHGNN 模型的形式化定义如下：

• 设 $h_t=S{b}_t\in {\mathbb{R}}^m$，其中 S∈{0,1}m×nS \in \{0,1\}^{m \times n}S∈{0,1}m×n 是加总矩阵，用于从底层序列 $b_t\in {\mathbb{R}}^n$ 聚合生成观测向量 $h_t\in {\mathbb{R}}^a$。
• 对于底层序列 $b_i$，在时刻 $t$ 的特征表示为 $f_{i,t}^b\in {\mathbb{R}}^{k_b^i}$，其中 $i=1,2,\dots ,n$。
• 对于高层聚合序列 $h_i$，在时刻 $t$ 的特征表示为 $f_{i,t}^h\in {\mathbb{R}}^{k_h^i}$，其中 $i=1,2,\dots ,a$。

此外，该模型还支持协变量（co-variates）、外部回归量（external regressors）以及层级结构的变化。

DeepHGNN 的优势在于利用图神经网络（GNN）在层级结构中传播信息：

• GNN 能够学习层级不同层次间的关系及其对应的特征，
• 进而捕捉底层序列与高层序列之间的依赖关系，
• 并充分利用所有层级的信息，从而提升预测精度。

与传统假设 层级固定 的分层预测模型不同，DeepHGNN 在训练过程中可以动态调整邻接矩阵 $A$，从而适应随时间变化的层级结构。这一特性对于关系不断演化的动态环境尤为关键。
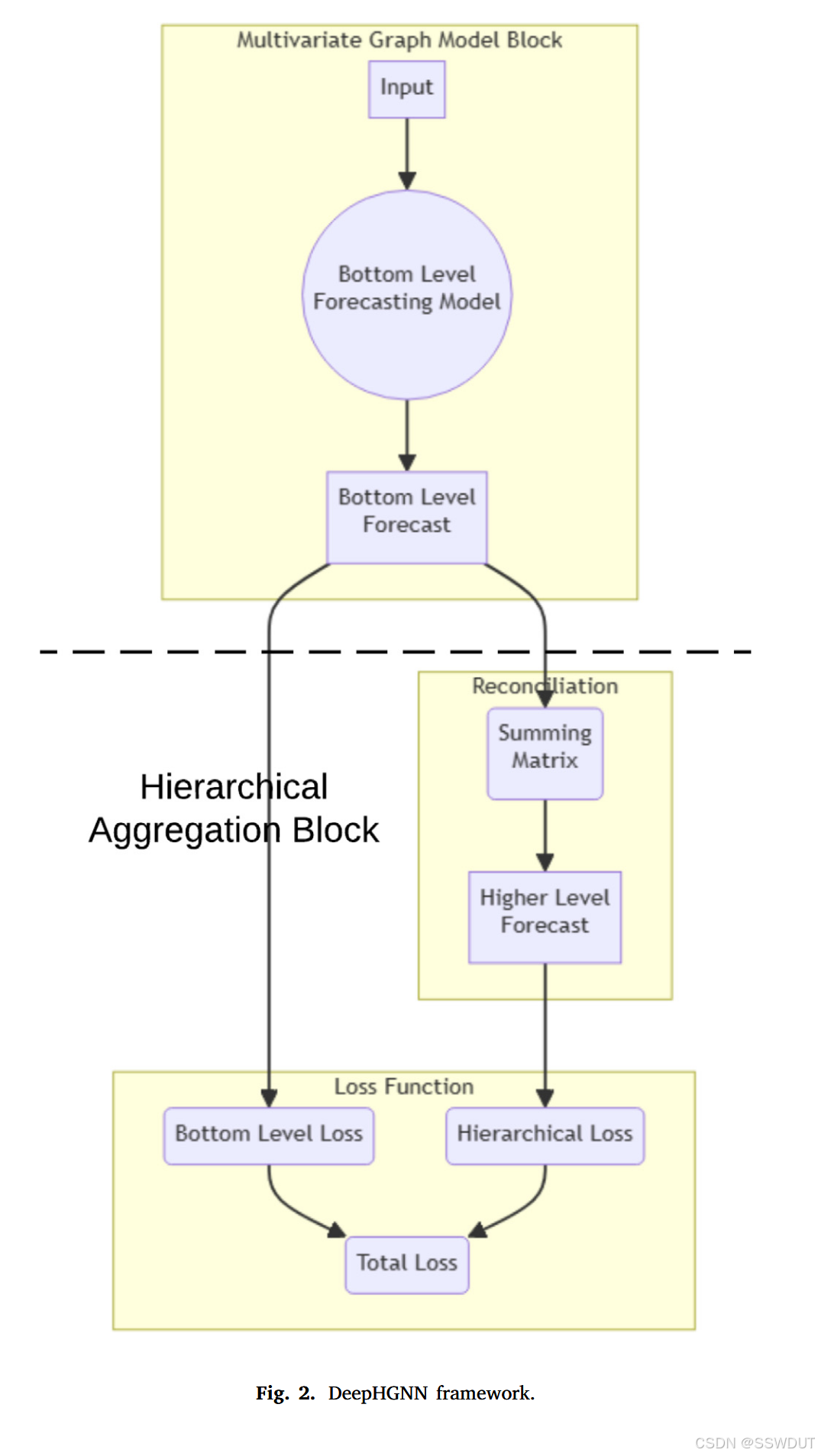
如图 2 所示，DeepHGNN 由两个主要模块构成：

1. 多变量图模型（MGM）模块：可以采用任意多变量预测的 GNN，用于建模时空模式；
2. 分层聚合模块：接收多变量时间序列的预测（形状为 节点数 × 预测步长 × 输出特征数），并输出经分层对账后的预测结果。
   

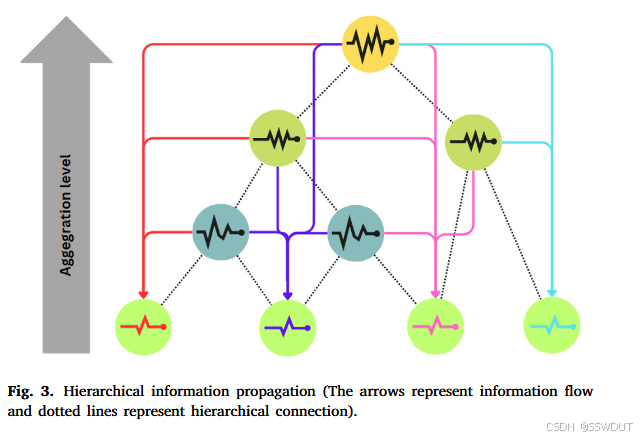
3.1. 多变量图模型（MGM）模块

MGM 模块主要用于底层序列的预测。其关键优势在于：在建模目标序列时，能够融合来自其父节点及祖先节点的信息。
图模型的使用意义在于：它允许预测过程考虑层级中不同序列之间的关系与依赖，而不是将各序列孤立处理。
例如：

• 在零售场景（图 3），门店销售额会受到区域趋势的影响，而区域趋势又受国家整体条件影响。
• 当 MGM 模块生成预测时，它会利用祖先层级的当前状态，从而避免单序列孤立建模带来的信息缺失。

由于层级越高，信号噪声比通常越高，因此图模型能借助这种 信号更强的上层信息 来提升预测精度。

3.2. 分层聚合模块

分层聚合模块执行 自底向上的对账，将底层预测逐步汇总生成高层预测，具体步骤如下：

1. 由 MGM 模块得到底层时间序列预测 ${\hat{b}}_t\in {\mathbb{R}}^n$，输入特征为 $f_{i,t}^b\in {\mathbb{R}}^{k_b^i}$；
2. 使用加总矩阵 S∈{0,1}m×nS \in \{0,1\}^{m \times n}S∈{0,1}m×n 将底层预测聚合为高层预测：
   $${\hat{h}}_t=S{\hat{b}}_t$$
3. 递归执行步骤 2，直至生成所有层级的预测 ${\hat{h}}_t\in {\mathbb{R}}^m$，直至最顶层预测。

损失函数 定义为：
$$L(\theta )=\sum _{t\in T_0}l(b_t,{\hat{b}}_t(\theta ))+\lambda \sum _{t\in T_0}l(h_t,{\hat{h}}_t(\theta ))$$
其中：

• $T_0$：训练集，
• $l(\cdot )$：损失函数（如 MSE），
• $\theta$：模型参数，
• $b_t$：真实底层序列，${\hat{b}}_t(\theta )$：底层预测序列，
• $h_t$：真实高层序列，${\hat{h}}_t(\theta )$：对账后的高层预测序列，
• $\lambda$：控制聚合层级损失的权重。

这种 分层损失函数 结合了底层预测误差与自底向上聚合预测误差，具有以下优势：

1. 提供全局性优化目标 —— 不仅关注某一层级，而是同时优化多个层级的预测；
2. 防止模型过拟合到某一层级，提高整体预测稳定性；
3. 对账过程起到正则化作用，强制预测结果在层级间保持逻辑一致；
4. 允许联合优化底层与高层预测精度，提升模型的稳健性与校准性；
5. 通过调整权重超参数 $\lambda$，可以灵活平衡底层预测与高层预测的重要性，以适应不同应用场景的需求。

4. 实验设置

本节详细介绍了数据集、对比方法、性能指标以及实验设置中的其他特征。

图 4. Favorita 数据集的层级结构

4.1. 数据集与性能指标

1. Favorita 数据集：该数据集（Corp. Favorita, 2017）来自 Kaggle 举办的一项销售预测竞赛，包含 2013 年 1 月至 2017 年 8 月间的杂货商品销售历史，以及促销信息、商品与门店的元数据。我们基于门店、城市和州构建了一个地理层级，包含 4500 个节点和 4 层聚合结构。时间步 1681 至 1687 作为长度为 7 的测试窗口，时间步 1 至 1686 用于训练和验证。其层级结构如图 4 所示。

2. 澳大利亚旅游数据集：该数据集包含澳大利亚国内游客数量的月度数据，涵盖 7 个州和领地，每个州进一步划分为地区、子地区和访问类型。该数据集大约包含 500 个节点，共 230 个时间步。时间步 1 至 221 用于训练和验证，测试指标在时间步 222 至 228 上计算。

3. M5 数据集：该数据集（M5, 2020）来自 Kaggle 举办的另一场销售预测竞赛，包含美国 3 个州 10 家沃尔玛门店的历史商品销售数据，以及商品层级和门店信息。参考 Paria 等人（2021），我们仅使用了商品层级。该数据集包含 3000 个节点和 4 层聚合结构。时间步 1907 至 1913 作为长度为 7 的测试窗口，时间步 1 至 1906 用于训练和验证。

为了评估性能，我们使用 绝对误差类指标，并与各方法的中位数预测结果进行比较：

• 加权绝对百分比误差（WAPE）：衡量真实值与预测值之间的平均百分比误差，并根据真实值的大小加权。公式如下：

$$\text{WAPE}=\frac{{\sum }_{(i,\tau )\in {\Omega }_{Test}}\Vert Y(i,\tau )-\hat{Y}(i,\tau )\Vert \cdot |Y(i,\tau )|}{{\sum }_{(i,\tau )\in {\Omega }_{Test}}|Y(i,\tau )|}$$

• 平均绝对缩放误差（MASE）：类似于 MAE，但按朴素预测的误差进行缩放。公式如下：

$$\text{MASE}=\frac{1}{\hat{N}}\sum _{(i,\tau )\in {\Omega }_{Test}}\frac{|Y(i,\tau )-\hat{Y}(i,\tau )|}{\frac{1}{N}{\sum }_{(i,t)\in {\Omega }_{Train}}|Y(i,t)-\tilde{Y}(i,t)|}$$

其中，$\tilde{Y}(i,t)$ 为朴素预测，$Y(i,t)$ 为真实值，$\hat{Y}(i,t)$ 为模型预测值。模型超参数遵循原始文献中的设定，以确保结果可与已有研究进行对比。

4.2. 对比方法

由于本文聚焦于 点预测，但部分对比方法提供的是 概率预测，因此在这些情况下我们取其 P50（中位数）预测。

• 基线与当前最先进方法

  • Fedformer：结合 Transformer 与季节–趋势分解方法，先分解时间序列以提取全局信息，再使用频域增强 Transformer 捕捉更精细的结构。
  • RNN-GRU：一种处理序列数据的循环神经网络。
  • ARIMA：统计模型，通过过去值预测未来值，由自回归（AR）、移动平均（MA）和积分（I）三部分组成。
  • ETS：指数平滑方法，使用加权的历史观测值预测未来。
  • DPMN：见第 2.2.5 节。
  • NBeats-SHARQ：一种混合模型，包含双残差堆叠的全连接层，再与 SHARQ 结合。
  • Hier-E2E：见第 2.2.4 节。
  • HIRED：见第 2.2.2 节。
  • PROFHIT：见第 2.2.3 节。

• 提出的层级端到端图神经网络方法
  DeepHGNN 指在基模型上堆叠层级聚合模块，并利用层级结构的邻接矩阵进行端到端优化。

  • DeepHGNN-DCRNN：以 DCRNN 为基模型（见第 2.1.1 节）。
  • DeepHGNN-MTGNN：以 MTGNN 为基模型（见第 2.1.2 节）。
  • DeepHGNN-ADLGNN：以 ADLGNN 为基模型（见第 2.1.3 节）。
  • DeepHGNN-MTGODE：以 MTGODE 为基模型（见第 2.1.4 节）。
  • DeepHGNN-ASTGCN：以 ASTGCN 为基模型（见第 2.1.5 节）。
  • DeepHGNN-GRAMODE：以 GRAMODE 为基模型（见第 2.1.6 节）。
  • DeepHGNN-SpecTGNN：以 SpecTGNN 为基模型（见第 2.1.7 节）。

4.3. 其他 GNN 模型

近期层级时间序列预测的一条研究方向是 HiGP（Cini, Mandic, & Alippi, 2023），该方法通过图池化学习层级，从数据中发现新的“超节点”。在这种框架下，不假设加和矩阵：模型直接优化所有新形成层级的预测，相当于自下而上生长出一个层级结构。

相比之下，本文提出的 DeepHGNN 针对的是 层级已知且必须遵循的场景（如门店–区域–国家），确保对既定层级结构的预测结果进行一致化，即使层级随时间发生变化（如公司重组），模型也会强制与更新后的层级对齐。

因此，两者服务于不同需求：

• HiGP 适合不存在固定层级、需要从数据中推断新聚类的情况；
• DeepHGNN 适合层级已知且必须被尊重的情况，保证在实际应用中（组织、法律或财务规则限制下）保持一致性。

在层级预测之外，近年来还提出了许多 GNN 方法，例如 TANGO（Huang et al., 2023）、ST-Neural ODEs 用于城市流量预测（Zhou et al., 2021），以及多种先进的 GNN 架构（Wang 等, 2022; 2024）。这些方法展示了图神经网络与神经 ODE 在时空数据中的潜力，也可能成为未来研究的强大基模型。

然而，本文的主要目标并非设计新的 GNN 主干网络，而是提出一个可以附加在任意多变量 GNN 预测器上的 层级一致化模块。因此，我们的对比重点在于 不同 GNN 方法在加入层级模块后性能的比较。值得注意的是，TANGO 等 GraphODE 方法若与 DeepHGNN 的一致化模块结合，可能进一步提升预测性能。

4.4. 与对比方法的区别

提出的 DeepHGNN 框架将：

1. 基于 GNN 的时空特征提取器，与
2. 端到端的层级一致化机制

统一到一个联合训练的流水线中。

• 传统层级预测流程通常为：先对每个序列独立预测（如 ARIMA、ETS、RNN），再通过自上而下、自下而上或 MinT 方法进行事后调整。其缺陷是：

  1. 预测时各序列相互独立；
  2. 一致化依赖强假设。

• 相比之下，DeepHGNN 在模型架构与损失函数中直接引入层级约束，同时学习底层预测与其聚合结果，降低了一致化误差，并在大规模或噪声较多的层级中提升鲁棒性。

• 一些最新方法也尝试在统一框架中引入层级约束（如 DPMN、Hier-E2E、HIRED、PROFHIT）。但 DeepHGNN 的不同之处在于：

  • 内嵌一个通用 GNN 主干，能够同时建模 节点级与层级间关系；
  • 使用邻接矩阵编码层级关系，在父子节点、兄弟节点、祖先节点之间传播信息，而不仅限于父子传递；
  • 上层节点信号通常更稳定可预测，GNN 可借助这些信号提升底层预测精度；
  • 端到端训练在所有层级间天然保持一致性。

4.5. 实验配置

训练数据集划分为 训练集（80%） 与 验证集（20%），最后一个时间窗口用于测试。模型训练时超参数采用原始实现中的推荐值。训练过程中设置了 早停机制，当验证集指标超过 4 个周期未改善时提前停止训练。

5. 结果与讨论

表2展示了所提出方法与其他现有方法的实验结果。从结果中可以观察到，我们提出的 DeepHGNN 模型的多个变体在 MASE 和 WAPE 两个指标上都 consistently 优于现有模型。其中，DeepHGNN-specTGNN 是整体表现最好的模型。

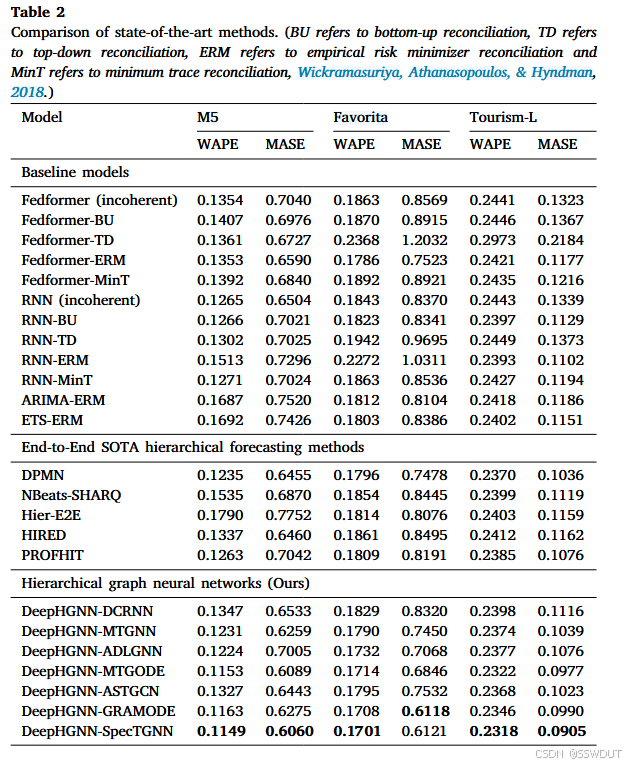
每次实验运行重复五次，每次都从头开始重新训练模型，并对误差指标取平均。基线模型包括 Fedformer 和 RNN 的多种配置，以及带有 ERM 的传统方法 ARIMA 和 ETS，它们在不同数据集上的表现差异较大。RNN 模型总体上优于 Fedformer，但仍不及更先进的方法。特别是，传统模型（如带 ERM 的 ARIMA 和 ETS）误差率较高，突出了传统方法在此类任务中的局限性。

在端到端的 SOTA 分层预测方法中，DPMN 表现较为突出。其他方法如 NBeatsSHARQ、Hier-E2E、HIRED 和 PROFHIT 虽然在方法上具有创新性，但仍表现出中到高的误差率。表3中的相对提升结果不仅强调了 DeepHGNN 的有效性，还突出了图神经网络方法在分层预测中的潜力。

为了评估统计显著性，我们采用了 Demšar (2006) 提出的关键差异图（CD diagram），并结合 Benavoli, Corani, Mangili (2016) 的改进方法，使用 Bunse (2023) 提供的 Python 实现。具体来说，我们先应用 Friedman 检验 来判断性能差异，再使用带有 Holm 校正 的 Wilcoxon 符号秩检验 处理多重比较。

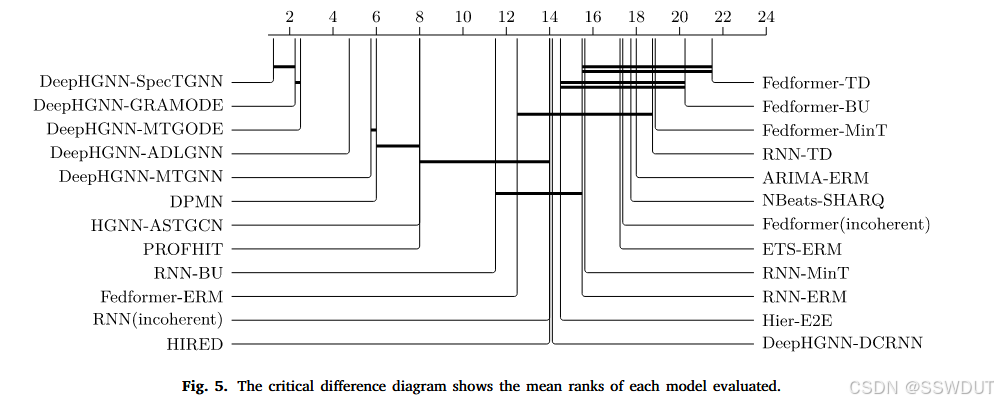
图5中的关键差异图展示了结果。图中基于 WAPE 指标给出了各模型的平均排名，排名越低表示准确率越高。通过水平线连接的模型被认为性能差异不显著，而没有连线的模型性能差异则显著。

可以看到，DeepHGNN 系列模型（DeepHGNN-SpecTGNN、DeepHGNN-GRAMODE、DeepHGNN-MTGODE、DeepHGNN-ADLGNN、DeepHGNN-MTGNN、DeepHGNN-ASTGCN） 聚集在图的左侧，显示出其优越性能。其中 DeepHGNN-SpecTGNN 位于最左端，反映其为表现最佳的模型。相对而言，DPMN、PROFHIT 以及 Fedformer、RNN 的各种变体集中在中部和右侧，而基于 ARIMA 和 ETS 的传统基线模型位于最右侧，表明其预测性能最差。

DeepHGNN 模型与其他方法之间的相对距离表明，其改进不仅是 增量性的，而是 显著且具有统计学意义的，验证了该方法的普适性。特别是，前几种性能最佳的 DeepHGNN 模型（SpecTGNN、GRAMODE、MTGODE、ADLGNN）与其余模型之间没有连接线，说明它们与基线和 SOTA 模型相比在性能上有 稳健的统计学显著差异。

表3 比较分析：DeepHGNN 前三名模型相较于现有 SOTA 方法在 WAPE 上的误差下降百分比

模型	M5	Favorita	Tourism-L	Overall
DeepHGNN-MTGODE	6.640%	4.566%	2.025%	3.925%
DeepHGNN-GRAMODE	5.830%	4.900%	1.012%	3.406%
DeepHGNN-SpecTGNN	6.964%	5.290%	2.194%	4.314%

5.1. 计算复杂度

由于 DeepHGNN 的 多变量图模型（MGM）块 可以由任意多变量预测 GNN 实现（如 ADLGNN、MTGNN），其计算开销主要取决于所选的 GNN 架构。总体而言，计算时间大多消耗在 基于图的消息传递 上，其复杂度取决于邻接矩阵是稀疏还是稠密。
在此，我们关注 DeepHGNN 在基础 GNN 之外引入的额外开销：

• 每次分层汇总需要将底层预测（形状 n × H）与求和矩阵 S ∈ {0, 1}m×n 相乘，代价为 O(m × n)。
• 当有多层时，此过程会在层级结构上递归进行，总复杂度为 O(K × m × n)，其中 K 为层数。

由于实际层级通常较浅（K ≈ 3–5），且高层节点数量远少于底层（m ≪ n），因此开销近似线性，相较于 GNN 训练来说开销很小。

相比之下，传统方法如 ARIMA、ETS 在大规模层级中需要对每个底层序列独立建模，训练代价为 O(N) × 单序列复杂度。如果再进行事后对齐（如 MinT），最坏情况下需要 O(N³) 的矩阵运算。同样，双阶段深度学习流程（如独立训练 RNN/Transformer，再对齐）也需要对所有 N 序列分别运行一次，最后再统一对齐。

而 DeepHGNN 通过一次 GNN 运行即可内建序列间依赖关系，并在多层目标函数中加入底层和汇总层的误差。其梯度计算仅需处理 O(K) 层的预测聚合，开销相对基础 GNN 成本可以忽略不计。

因此，DeepHGNN 的总体运行时间与常规 GNN 预测管道在同一量级，仅在分层聚合和对齐上增加了轻量化的开销。

5.2. 消融实验

我们对 DeepHGNN-SpecTGNN 进行了消融实验，评估其端到端分层对齐的效果。去掉分层聚合模块后，得到 Base-GNN-NaiveSum：它仅在底层序列上使用 GNN（SpecTGNN），然后简单求和得到高层预测。

在该基线模型中，邻接矩阵只连接具有层级关系的底层序列（如同类产品、同一城市的商店），但不包括直接的高层节点。因此，它无法将父节点的聚合信号直接传递到底层，也无法跨层进行联合对齐。

表4 显示了在 M5 和 Favorita 数据集上两种方法的底层（MASE-B）和汇总层（MASE-A）误差：

模型	M5 MASE-B	M5 MASE-A	Favorita MASE-B	Favorita MASE-A
DeepHGNN-SpecTGNN (full)	0.605	0.610	0.612	0.613
Base-GNN-NaiveSum	0.615	0.638	0.623	0.651

• 底层准确率（MASE-B）：完整的 DeepHGNN-SpecTGNN 在底层略优于消融模型。M5 从 0.615 提升至 0.605，Favorita 从 0.623 提升至 0.612。尽管 Base-GNN-NaiveSum 可利用底层序列间的邻接信息，但缺乏来自高层的信号，预测稳定性不足。
• 汇总层准确率（MASE-A）：移除分层聚合影响更大。M5 的误差从 0.610 上升至 0.638，Favorita 从 0.613 上升至 0.651。这表明简单的底层预测求和会累积误差，而 DeepHGNN 的端到端对齐能确保层级内一致性，显著提高整体预测准确率。

这些结果说明，尽管底层 GNN 邻接连接能部分利用序列间关系，但只有完整的 DeepHGNN-SpecTGNN 允许 自上而下信息流动 并进行 显式多层对齐，因此在各层次上均表现更佳。

6. 结论

本文提出了一种 分层图神经网络（DeepHGNN） 方法，用于建模时间序列数据中的层级依赖关系。实验结果表明，将层级结构和对齐机制结合图神经网络后，预测准确率相比现有方法显著提升。

关键差异分析验证了 DeepHGNN 在多个数据集上误差显著低于 RNN、LSTM、时序卷积网络等流行基线。通过同时建模层级内和跨层交互，DeepHGNN 能生成更准确和一致的预测。它支持特征共享和对齐正则化，而这些是传统方法所缺乏的。

总的来说，结果强调了在图神经网络中显式编码领域层级约束的价值，证明了其在复杂层级时间序列预测问题中的潜力。DeepHGNN 的框架灵活，可以适配多种对齐约束和依赖关系。

尽管 DeepHGNN 在预测准确率上显著优于传统方法，但仍存在一些限制和挑战：

• 计算与内存开销：在层级非常庞大、包含数千序列的场景下，资源消耗迅速增加，限制了其在大规模复杂数据集中的适用性。
• 不确定性建模：目前 DeepHGNN 仅提供点预测，而许多实际应用需要概率预测或区间预测，以便更好地进行风险管理和决策。未来研究可探索将分层对齐机制扩展到概率预测，提供预测区间或分布输出，从而提升在供应链管理、资源规划等高风险场景下的鲁棒性和可靠性。

本研究获得以下支持：

• Facebook Statistics for Improving Insights and Decisions 研究奖
• Monash University 研究生科研资助
• 澳大利亚 MASSIVE 高性能计算平台

此外，Christoph Bergmeir 目前由西班牙大学部和欧盟新一代基金资助的 María Zambrano（高级）研究员奖学金 支持。