一、题目解析

1、i<j且nums[i]>2*nums[j],(i,j)记作一个翻转对
2、nums长度不会超过50000
3、nums中所有元素都在32位整数范围内
二、算法原理
解法1:暴力枚举 O(N^2)
固定一个数,枚举另一个数
解法2:分治 O(N*logN)
计算翻转对 (利用单调性,使用同向双指针)
方法1:计算当前元素后面,有多少元素的两倍比我小(降序)

由于降序,nums[cur1]>nums[cur2]*2,即nums[cur1]比cur2后面的所有数大,所以cur2~right的个数为right-cur2+1
方法2:计算当前元素之前,有多少元素的一般比我大(升序)

除2.0为了避免除不尽的情况,由于升序,nums[cur1]/2.0>nums[cur2],nums[cur2]比cur1后面的所有数小,所以cur1~mid的个数为mid-cur1+1
合并两个有序数组

在升序中,tmp[i++] = nums[cur1]<=nums[cur2] ? nums[cur1++] : nums[cur2++]
在降序中,tmp[i++] = nums[cur1]<=nums[cur2] ? nums[cur2++] : nums[cur1++]
三、代码示例
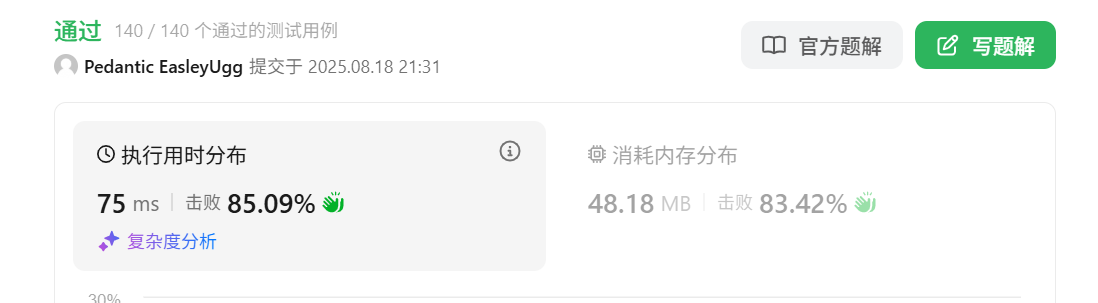
解法2:降序
int tmp[50005];
public://降序int reversePairs(vector<int>& nums){return mergeSort(nums,0,nums.size()-1);}int mergeSort(vector<int>& nums,int left,int right){int ret = 0;if(left>=right) return 0;int mid = (left+right)>>1;ret += mergeSort(nums,left,mid);ret += mergeSort(nums,mid+1,right);//统计翻转对int cur1 = left,cur2 = mid+1;while(cur1<=mid){while(cur2<=right && nums[cur1]/2.0 <= nums[cur2]) cur2++;if(cur2>right) break;ret += right-cur2+1;cur1++;}int curr1 = left,curr2 = mid+1,i = 0;while(curr1<=mid && curr2<=right)tmp[i++] = nums[curr1]<=nums[curr2] ? nums[curr2++] : nums[curr1++];//处理未遍历完while(curr1<=mid) tmp[i++] = nums[curr1++];while(curr2<=right) tmp[i++] = nums[curr2++];//还原for(int i = left;i<=right;i++)nums[i] = tmp[i-left];return ret;}
这里不是nums[cur2]*2原因是,虽然都是32位整数范围内,但是*2可能会导致积超过32位的范围,所以/2.0
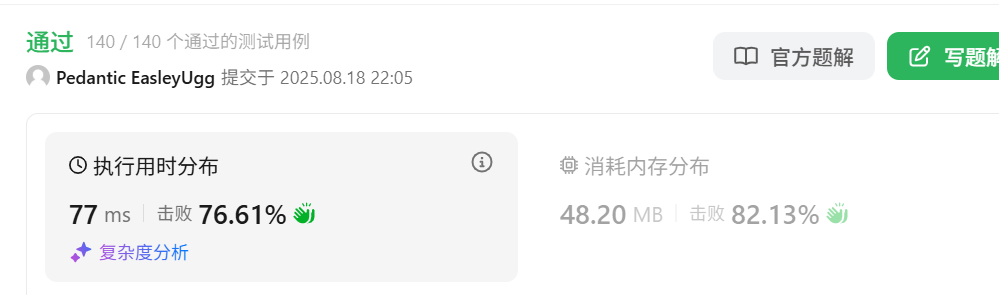
解法2:升序
int tmp[50005];
public:
//升序int reversePairs(vector<int>& nums){return mergeSort(nums,0,nums.size()-1);}int mergeSort(vector<int>& nums,int left,int right){int ret = 0;if(left>=right) return 0;int mid = (left+right)>>1;ret += mergeSort(nums,left,mid);ret += mergeSort(nums,mid+1,right);//统计翻转对int cur1 = left,cur2 = mid+1;while(cur2<=right){while(cur1<=mid && nums[cur1]/2.0 <= nums[cur2]) cur1++;if(cur1>mid) break;ret += mid-cur1+1;cur2++;}int curr1 = left,curr2 = mid+1,i = 0;while(curr1<=mid && curr2<=right)tmp[i++] = nums[curr1]<=nums[curr2] ? nums[curr1++] : nums[curr2++];//处理未遍历完while(curr1<=mid) tmp[i++] = nums[curr1++];while(curr2<=right) tmp[i++] = nums[curr2++];//还原for(int i = left;i<=right;i++)nums[i] = tmp[i-left];return ret;}
看到最后,如果对您有所帮助,还请点赞、收藏和关注,我们下期再见!






