深度学习——常见的神经网络

一、FNN

1.1原理

前馈神经网络（Feedforward Neural Network, FNN） 是最基础、最常见的人工神经网络结构。
其核心思想是：信息从输入层开始，经过若干个隐藏层的非线性变换，最终到达输出层，且信号只沿单向传播，不会形成循环。因此，FNN 又常被称为 多层感知机（MLP, Multi-Layer Perceptron）。

• 输入层（Input Layer）：接收原始数据特征，维度 = 输入特征数量。不进行计算，只负责数据传递。
• 隐藏层（Hidden Layer）：一个或多个隐藏层，每层由多个神经元组成。

单层神经元计算：
$$a=f(z)=f(W\cdot x+b)$$
其中：

• $W$ ：权重矩阵；$x$ ：输入向量；$b$ ：偏置；
• $f$ ：激活函数（如 ReLU, Sigmoid, Tanh 等）；$a$ ：神经元输出

多层网络（第 $l$ 层）：
$$a^{(l)}=f(W^{(l)}\cdot a^{(l-1)}+b^{(l)})$$

• 输出层（Output Layer）：将隐藏层结果映射到任务需求的输出维度。
  • 分类：Softmax 输出概率分布
  • 回归：线性输出

---

FNN 的训练主要依靠 反向传播（Backpropagation, BP） + 梯度下降（Gradient Descent）：

• 前向传播：计算预测输出。
• 计算损失：衡量预测值与真实值的误差（如 MSE, Cross-Entropy）。
• 反向传播：通过链式法则计算梯度。
• 参数更新：使用梯度下降（或优化器，如 Adam、SGD）更新参数。

1.2代码

class FNN(nn.Module):def __init__(self, input_size=10, hidden_size=32, output_size=2):super(FNN, self).__init__()self.fc1 = nn.Linear(input_size, hidden_size)  # 输入层 → 隐藏层self.relu = nn.ReLU()self.fc2 = nn.Linear(hidden_size, output_size)  # 隐藏层 → 输出层def forward(self, x):out = self.fc1(x)out = self.relu(out)out = self.fc2(out)return out

• input_size：每条输入数据的特征数量，也就是输入向量的长度。
• hidden_size：隐藏层中神经元的数量。
• output_size：输出层神经元的数量，决定网络的最终输出维度。
  • 分类任务：输出神经元数量 = 类别数。例如二分类 → output_size = 2，三分类 → output_size = 3。
  • 回归任务：输出神经元数量 = 需要预测的值的数量。

二、CNN

参考视频
https://www.bilibili.com/video/BV1MsrmY4Edi/?spm_id_from=333.337.search-card.all.click&vd_source=67ba3568cbf6ea1d930339cd0f2092ba

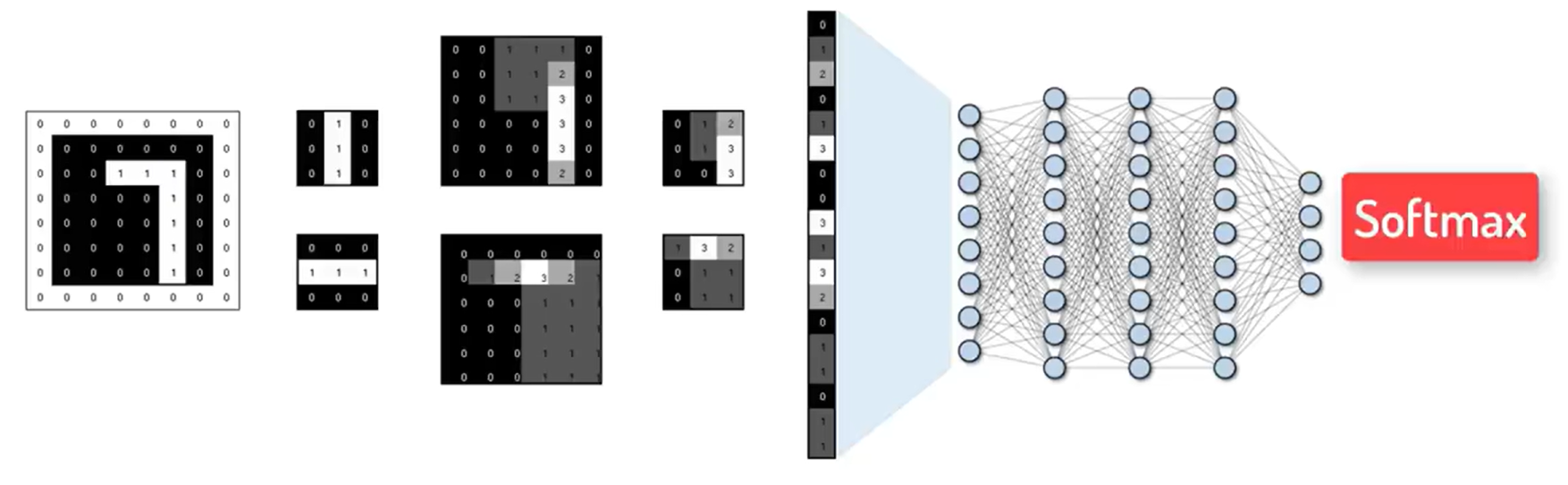
2.1原理

Step1：提取图片特征（+padding）

使用卷积核（特征过滤器）进行特征提取。

• 卷积核有2个，则会生成2张特征图
• 卷积核有多少个，就会生成多少张特征图
  

提取特征的计算规则：

• 滑动窗口：卷积核在输入图像上按照一定的步长（Stride）滑动，每次滑动都会计算一次卷积操作，得到特征图上的一个值。例如，步长为 1 时，卷积核每次移动一个像素；步长为 2 时，卷积核每次移动两个像素。
• 局部感知：卷积核的尺寸通常远小于输入图像的尺寸，这意味着它在每次运算时只关注图像的一个局部区域，从而提取局部特征。
• 权值共享：无论卷积核滑动到图像的哪个位置，其权值都保持不变，整个图像上是共享。这样大大减少了模型的参数数量，降低了计算复杂度，同时也提高了模型的泛化能力。

最终结果如下：原来66的图片被特征提取之后，大小变成了44，并且边缘特征都丢失了。

Padding：扩充0。使得原来6*6的图片在扩充之后边缘信息能被成功提取。
其主要的作用有：1、保持特征图尺寸2、保护边缘信息。其计算方法不展开叙述。

Step2：池化

池化操作与卷积类似，通过滑动窗口在特征图上移动，对每个窗口内的像素进行聚合计算。常见的有最大池化和平均池化。
池化的主要作用有1、保留边缘、纹理等显著特征2、将图片的大小变小：8 * 8的图片变成了4 * 4。

Step3：扁平化处理

将多维的输入数据拉平转换为一维向量 。
在 CNN 中，经过一系列卷积和池化操作后，输出的特征图通常是具有高度、宽度和通道数的三维张量（形状如 [batch_size, height, width, channels] ）；在 RNN 处理序列数据时，输出也可能是多维张量。而全连接层要求输入是一维向量，扁平化处理就是为了满足全连接层的输入要求。

2.2代码

class CNN(nn.Module):def __init__(self):super(CNN, self).__init__()self.conv1 = nn.Sequential( nn.Conv2d(in_channels=1,     out_channels=16,   kernel_size=5,      stride=1,          padding=2,     ),     nn.ReLU(),   nn.MaxPool2d(kernel_size=2),    )self.conv2 = nn.Sequentialnn.Conv2d(16, 32, 5, 1, 2),  nn.ReLU(), nn.MaxPool2d(2),  )self.out = nn.Linear(32 * 7 * 7, 10)  def forward(self, x):x = self.conv1(x)x = self.conv2(x)x = x.view(x.size(0), -1)   output = self.out(x)return output

• in_channels：输入的通道数（输入图片的“深度”）。
  • 灰度图：1 通道
  • RGB彩色图：3 通道
• out_channels：卷积核（滤波器）的数量，也就是输出的特征图（feature map）的数量
• kernel_size：卷积核的大小。
  • 如果写成整数 3，表示是 3x3 的卷积核。
  • 如果写成元组 (3, 5)，就是 3x5 的卷积核。
• stride：卷积的步幅。stride=1 表示卷积核每次滑动 1 个像素。如果 stride=2，就是每次跨 2 个像素，输出的特征图尺寸会缩小一半。
• padding：在输入的边缘补零（zero padding），用来控制输出大小。

过程	图片信息
输入	(batch_size, 1, 28, 28)
conv1+ReLu	(batch_size, 16, 28, 28)
pool	(batch_size, 16, 14, 14)
conv2+ReLu	(batch_size, 32, 14, 14)
pool	(batch_size, 32, 7, 7)
flatten	(batch_size, 10)

三、RNN

3.1CNN的问题

CNN的优点：

• 局部感受野：捕捉局部模式（如边缘、纹理）
• 权重共享：减少参数量
• 空间不变性：平移不影响特征提取

局限：

• 只能捕捉固定大小局部特征，对长距离依赖不敏感
• 不适合序列数据（文本、时间序列、语音等），因为 CNN 处理长序列需要非常深的网络才能捕捉远距离依赖。

3.2原理

RNN的核心思想：网络的隐藏状态记录历史信息，每个时间步的输出依赖当前输入和之前的隐藏状态。

隐藏状态是 RNN 的“记忆”，记录了从序列开头到当前时间步的历史信息。它本身不一定直接就是任务输出。维度通常是 hidden_size

隐藏状态更新： $$h_t=f(W_{xh}{x}_t+W_{hh}{h}_{t-1}+b_h)$$

• $W_{xh}{x}_t$ 本质上就是对当前输入 $x_t$做了全连接
  • $x_t$：当前输入
  • $W_{xh}$：权重矩阵
• $W_{hh}{h}_{t-1}$本质上就是对 上一时间步隐藏状态 $h_{t-1}$做了全连接
  • $h_{t-1}$：上一个时间步的隐藏状态
  • $W_{hh}$：权重矩阵
• $b_h$：偏置
• $f$：激活函数（如 tanh 或 ReLU）

将隐藏状态经过 线性映射 + 激活函数 得到最终输出：
$$y_t=g(W_{hy}{h}_t+b_y)$$

3.3代码

class RNNClassifier(nn.Module):def __init__(self, input_size=28, hidden_size=128, num_layers=2, num_classes=10):super(RNNClassifier, self).__init__()self.hidden_size = hidden_sizeself.num_layers = num_layers# RNN 输入: input_size=28, 输出 hidden_sizeself.rnn = nn.RNN(input_size=input_size, hidden_size=hidden_size,num_layers=num_layers, batch_first=True)# 输出层self.fc = nn.Linear(hidden_size, num_classes)def forward(self, x):# x.shape = (batch, 1, 28, 28)x = x.squeeze(1)  # 去掉通道维度, (batch, 28, 28)# 初始化隐藏状态h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_size).to(x.device)# RNN 前向传播out, _ = self.rnn(x, h0)  # out: (batch, seq_len=28, hidden_size)out = out[:, -1, :]        # 取最后一个时间步out = self.fc(out)return out

• 时间步 time step：指序列中每一个单独的输入点。假设一句话是 “HELLO”，则每个字母是一个时间步，共5个时间步。
• input_size：每个时间步输入的特征维度。每张图 28x28，我们把每一行的28个像素当作一个时间步。
• 序列长度 seq_len：一共有28个时间步。因此序列长度为28.
• hidden_size：hidden_size 想象成 RNN 的记忆容量。数值越大，网络容量越强，但参数更多，计算量更大。$h_t$是 hidden_size 维的向量。
• num_layers：RNN 堆叠的层数
  • num_layers=1 → 单层 RNN
  • num_layers>1 → 多层 RNN，每一层的输出作为下一层的输入
• batch_first：指定输入和输出张量的维度顺序
  • True → 输入和输出张量形状为 (batch_size, seq_len, input_size)
  • False → 输入和输出张量形状为 (seq_len, batch_size, input_size)

整体 X 是 (batch_size, seq_len, input_size)。RNN 内部会把序列拆开，每个时间步输入:

名称	形状	说明
$单时间步x_t$	(batch_size, input_size)	当前时间步输入向量，送入RNNcell
$隐藏状态h_t$	(batch_size, hidden_size)	当前时间步的隐藏状态
$输出y_t$	(batch_size, output_size)	当前时间步输出（分类概率等）

四、LSTM

4.1RNN的问题

RNN 的问题：

• 梯度消失 / 梯度爆炸：时间步太长时，梯度在反向传播中可能衰减得太快或爆炸。
• 训练慢：必须按时间步循环计算，难以完全并行。
• 长序列依赖难：标准 RNN 难以捕捉很长的依赖关系。

参考视频
https://www.bilibili.com/video/av15997678?spm_id_from=333.788.videopod.episodes&aid=15997678&vd_source=67ba3568cbf6ea1d930339cd0f2092ba&p=21

4.2原理

为了解决这个问题，LSTM （long-short term memory）引入了一种门控机制来控制信息的“遗忘、记忆和输出”。

LSTM 在结构上比 RNN 多了一条细胞状态（cell state，记忆线），像是一条传送带，能让信息更容易在序列中流动。 它通过三个门来调控信息流动：

• 遗忘门（Forget Gate）：决定哪些历史信息要丢掉。
  $$f_t=\sigma (W_f\cdot [h_{t-1},x_t]+b_f)$$
  • 输入：上一步隐藏状态 (h_{t-1}) 和当前输入 (x_t)
  • 输出：一个 0~1 之间的向量，接近 0 表示遗忘，接近 1 表示保留
• 输入门（Input Gate）：决定哪些新信息要存入记忆。
  $$i_t=\sigma (W_i\cdot [h_{t-1},x_t]+b_i)$$ $${\tilde{C}}_t=\tanh (W_C\cdot [h_{t-1},x_t]+b_C)$$
  • $i_t$：控制要写入多少新信息
  • ${\tilde{C}}_t$：候选的新记忆
• 更新细胞状态：结合遗忘门和输入门，更新记忆：
  $$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t$$
• 输出门（Output Gate）：决定输出多少信息作为隐藏状态 (h_t)。
  $$o_t=\sigma (W_o\cdot [h_{t-1},x_t]+b_o)$$ $$h_t=o_t\ast \tanh (C_t)$$

---

在每个时间步 $t$：

1. 遗忘门决定丢掉多少旧信息；
2. 输入门决定接收多少新信息；
3. 更新细胞状态 $C_t$，相当于“长期记忆”；
4. 输出门生成新的隐藏状态 $h_t$，作为“短期记忆”，传给下一步。

---

LSTM 的优势：

• 能有效缓解 RNN 的梯度消失问题；
• 可以记住长期依赖信息（比如一段话开头的信息影响后面很远的词）；
• 在 NLP、语音识别、时间序列预测等任务上表现良好。

4.3代码

其代码和CNN类似：

class LSTMClassifier(nn.Module):def __init__(self, input_size=50, hidden_size=128, num_layers=2, num_classes=2):super(LSTMClassifier, self).__init__()self.lstm = nn.LSTM(input_size=input_size,hidden_size=hidden_size,num_layers=num_layers,batch_first=True)  # 输入格式 (batch, seq_len, input_size)self.fc = nn.Linear(hidden_size, num_classes)def forward(self, x):# h0, c0 默认初始化为 0out, _ = self.lstm(x)       # out: (batch, seq_len, hidden_size)out = out[:, -1, :]         # 取最后一个时间步的隐藏状态out = self.fc(out)          # 全连接层分类return out

五、GRU

5.1原理

普通 RNN 难以捕捉长距离依赖，易出现梯度消失/爆炸。GRU（2014, Cho 等）通过门控机制控制信息流动，像 LSTM 一样缓解长依赖问题，但结构更简洁、参数更少、训练更快。

GRU 只有一个状态（隐藏状态$h_t$），没有像 LSTM 那样独立的细胞状态 $C_t$。它通过两个门来调控：

• 更新门（Update Gate）：决定保留多少旧信息、引入多少新信息。
  $$z_t=\sigma (W_z{x}_t+U_z{h}_{t-1}+b_z)$$
  • $z_t\approx 0$：几乎复制 $h_{t-1}$，保留长程记忆。
  • $z_t\approx 1$：几乎采用 ${\tilde{h}}_t$，快速更新为新状态。
• 重置门（Reset Gate）：决定在计算候选状态时，旧信息参与多少。
  $$r_t=\sigma (W_r{x}_t+U_r{h}_{t-1}+b_r)$$
  • $r_t\approx 0$：近似抛开历史，只看当前输入 $x_t$。
  • $r_t\approx 1$：结合历史与当前信息更新状态。
• 候选隐藏状态
  $${\tilde{h}}_t=\tanh (W_h{x}_t+U_h(r_t\odot h_{t-1})+b_h)$$
• 最终状态更新（线性插值）
  $$h_t=(1-z_t)\odot h_{t-1}+z_t\odot {\tilde{h}}_t$$

---

与 LSTM 的对比：

方面	GRU	LSTM
状态	只有 $h_t$	有 $C_t$（细胞）和 $h_t$
门的数量	2 个（更新、重置）	3 个门 + 候选（遗忘、输入、输出 + 候选）
参数量	约 3×(D·H + H² + H)	约 4×(D·H + H² + H)
速度/内存	更快、更省	略慢、略占内存
记忆力	通常与 LSTM 接近	某些长依赖任务可能更稳

5.2代码

class GRUClassifier(nn.Module):def __init__(self, input_size, hidden_size, num_layers, num_classes, bidirectional=False):super().__init__()self.gru = nn.GRU(input_size=input_size,hidden_size=hidden_size,num_layers=num_layers,batch_first=True,bidirectional=bidirectional)factor = 2 if bidirectional else 1self.fc = nn.Linear(hidden_size * factor, num_classes)def forward(self, x):                out, h_n = self.gru(x)         feat = out[:, -1, :]             logits = self.fc(feat)          return logits

上述原理图片来源：
https://github.com/NLP-LOVE/ML-NLP/blob/master/Deep%20Learning/12.2%20LSTM/README.md