Zemax 中的透镜设计 - 像差理论
每个光学系统,无论制作得多么精心,都会偏离完美。所有光学系统都包含 Blur。模糊来自 2 个来源,衍射和像差。衍射是一种物理限制,因为发现光线会在拐角处弯曲并导致模糊。像差是由光学器件甚至光纤的缺陷引起的。
19 世纪中叶,路德维希·冯·塞德尔 (Ludwig von Seidel) 正式确定了一组五个三阶像差(三阶和四阶是相同的,这是一个非常不幸的命名约定,因为在笛卡尔坐标中的波像差方程中,塞德尔像差是三阶,但在极地形式中它们是四阶)像差,这些像差在所有旋转对称光学系统中都很常见。
本文将从三个互补的角度探讨这些四阶像差:
- 数学上:通过波像差函数
。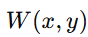
- 物理上:通过射线行为和直观的解释。
- 起源:它们如何在真实的光学系统中产生。
波像差函数:起点
在命名像差之前,我们定义了波像差函数。
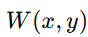
是实际波前与收敛到高斯焦点的理想球面参考波之间的光程差 (OPD)。
在出瞳中,完美的波前是半径为 R 的球形:
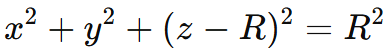
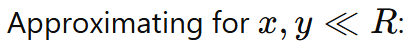
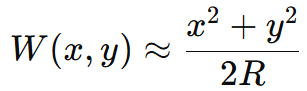
像差是偏离这个完美的抛物面形状,在上面的函数中引入额外的项,可以用出瞳坐标表示:
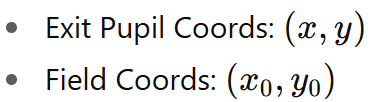
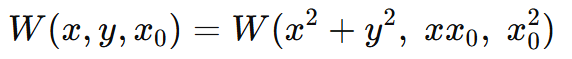
从理想的抛物面形状到全像差展开的这一关键步骤是认识到波前可以表示为瞳孔坐标
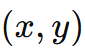
和场坐标的幂级数
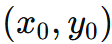
。
一般横射线波前方程变为:
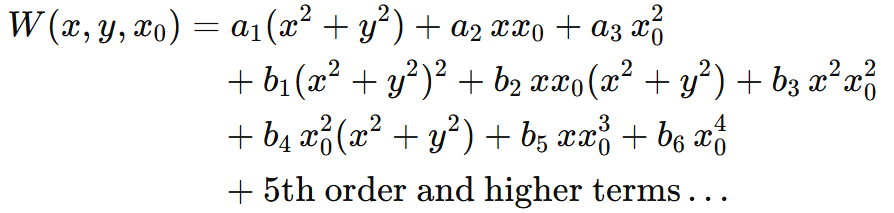
- a1 -> 散焦
- a2 -> 倾斜
- a3 -> 活塞
- b1 - b5 -> 球面、彗差、散光、场曲率、畸变(塞德尔像差)等......
由于大多数光学系统具有旋转对称性,最常用的极坐标形式可以用归一化瞳孔坐标和场坐标来写,其中:
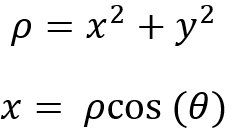
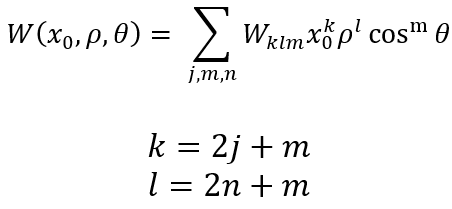
Expanded 给出了最流行的形式:
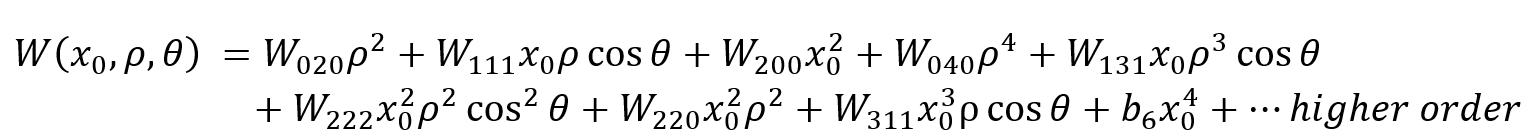
这是最方便的形式,因为每个索引对应于每个坐标的幂,它告诉我们为什么我们的光学系统中存在特定的像差。
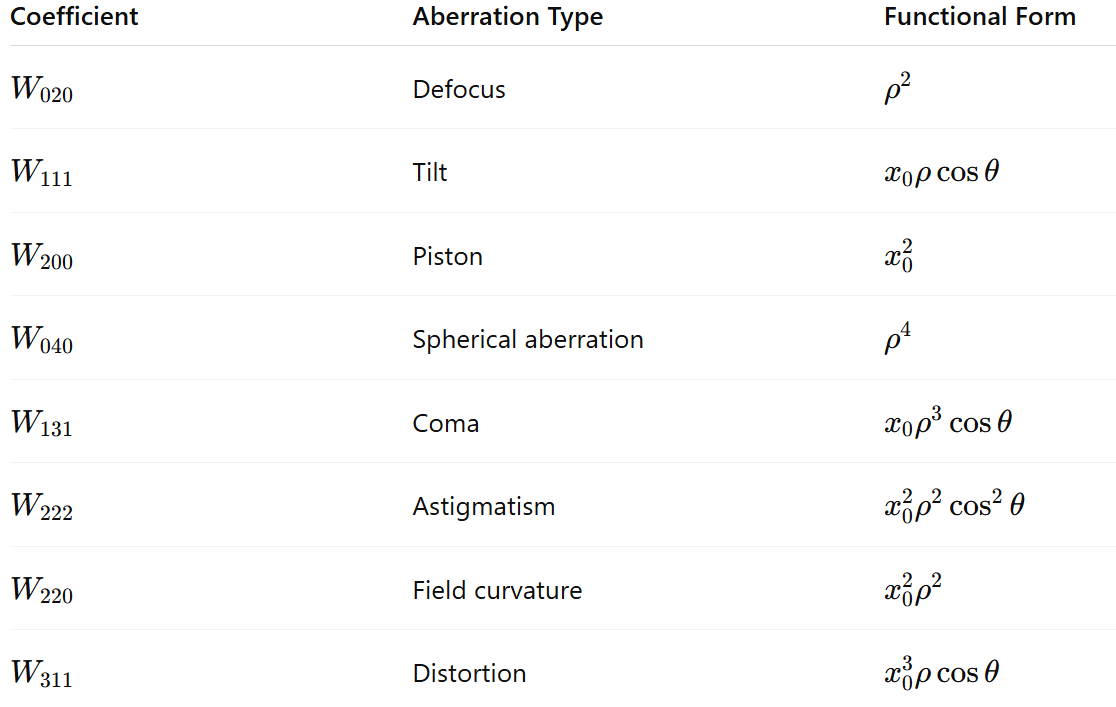
使用系数是记住波前在出瞳中关系的简单方法。
球形
场坐标不存在,因此在场上是恒定的。这意味着这是一种轴上像差。在图像中,来自轴上物体点的光线将与高斯焦点前面或后面的轴相交。光线越靠近瞳孔边缘,波前偏差越大,聚焦速度越快。靠近瞳孔中心的光线聚焦速度会变慢。这源于晶状体表面在瞳孔上不均匀地弯曲光线。
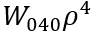
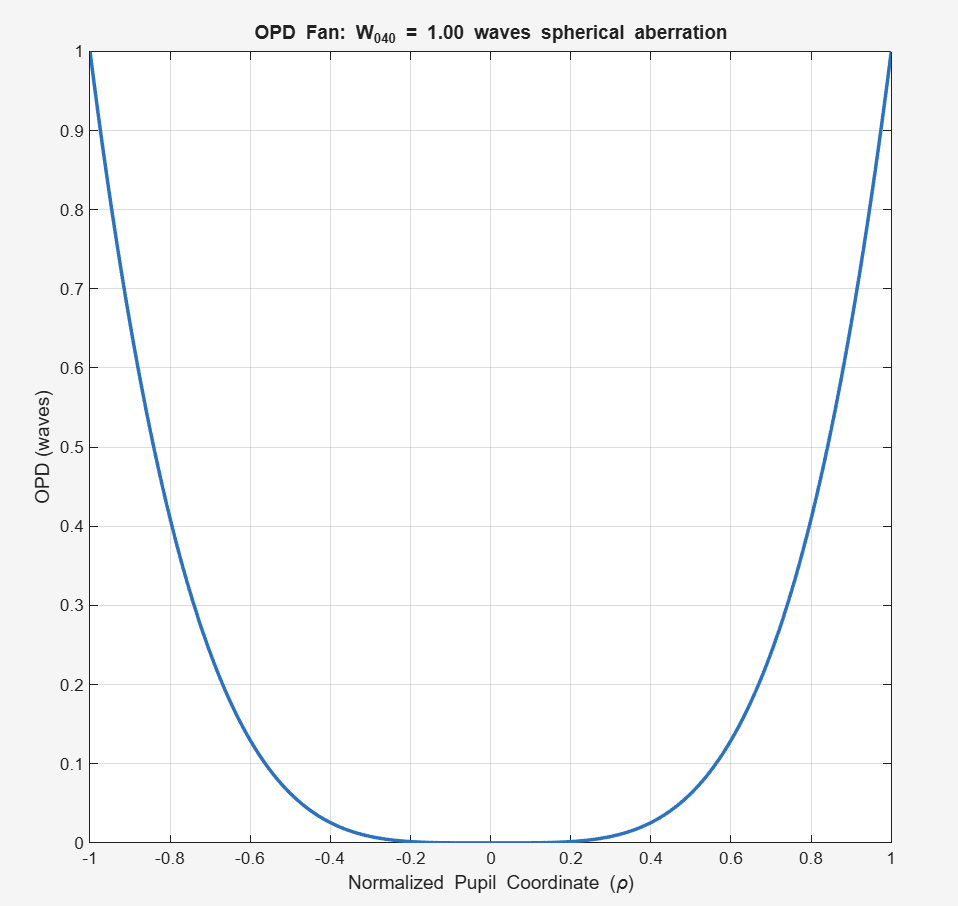
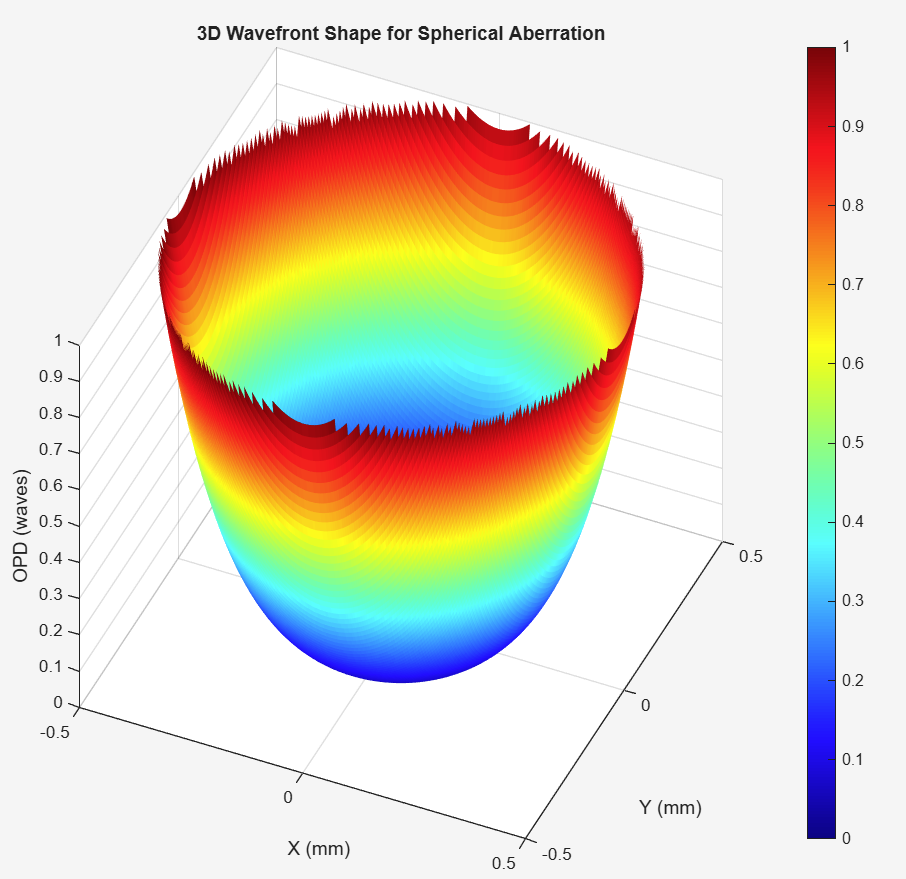
左侧的图与 Zemax 中的 OPD 风扇相同,右侧的图是 OPD 风扇的 3D 视图。
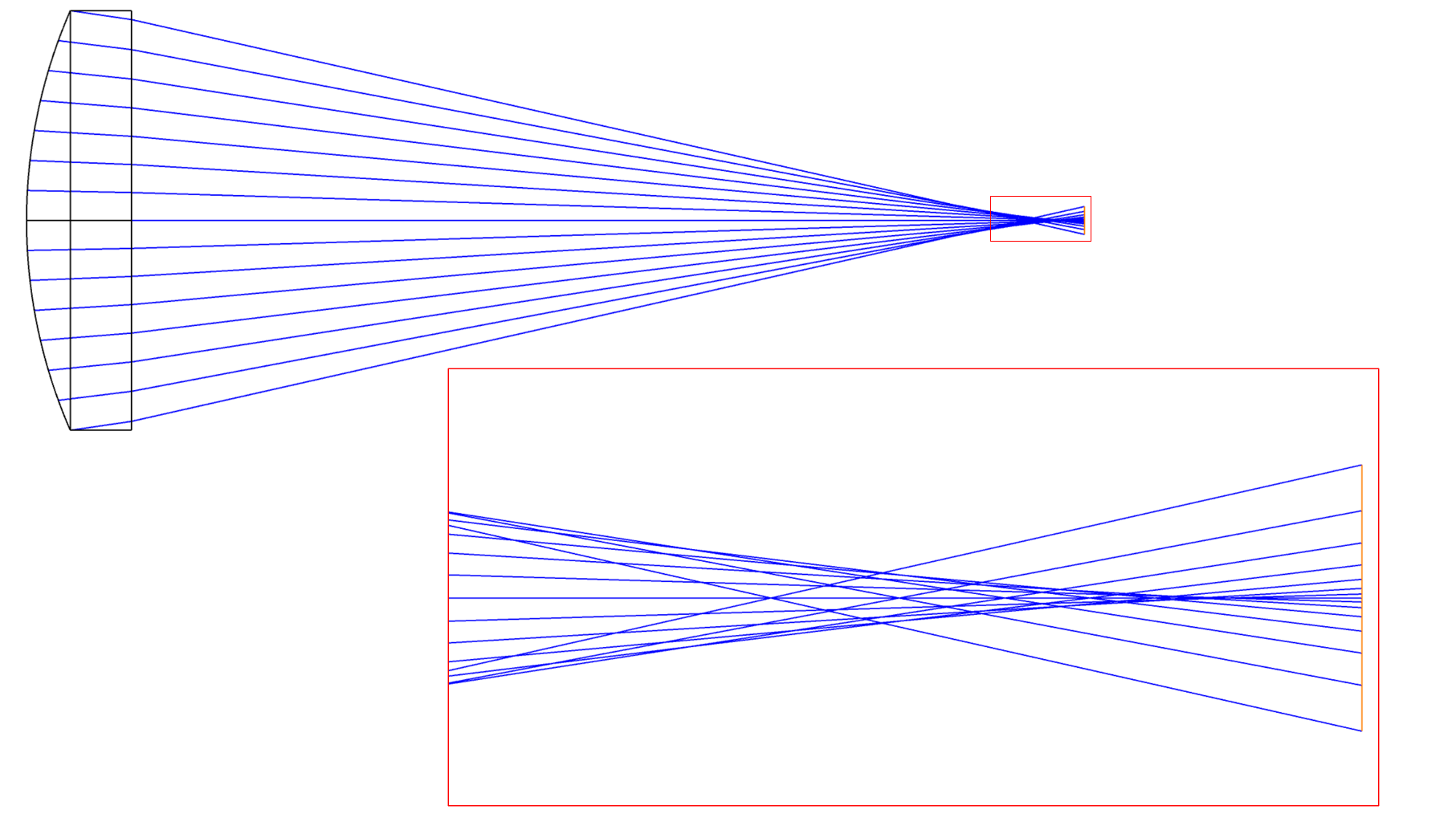
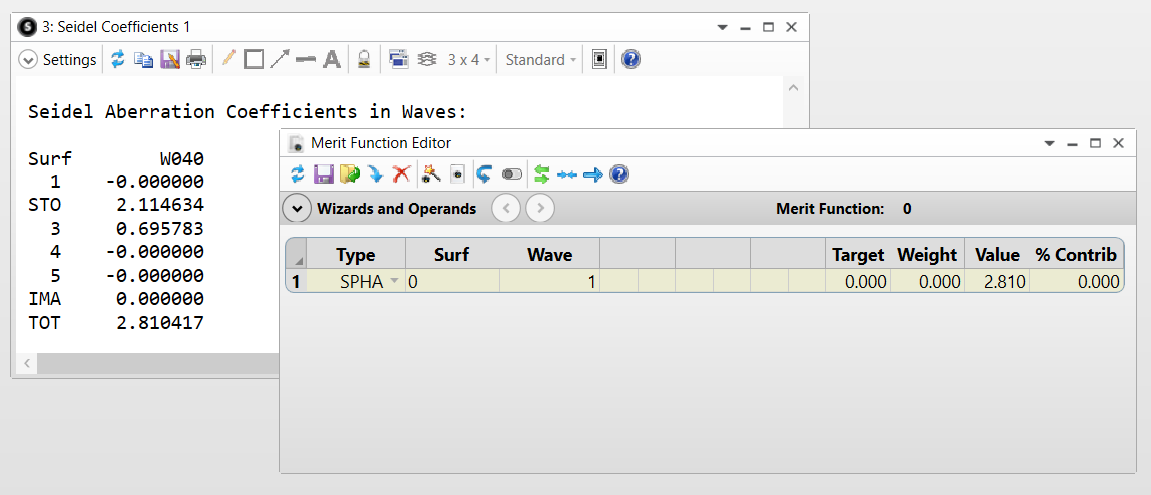
注意注意力不集中。焦距有一个函数,径向取决于您在瞳孔中的位置(这里瞳孔是镜头本身)。与 Spherical 关联的自定义作数是 SPHA。在系统中查看球形的另一个地方是分析 -> 像差 -> 塞德尔系数
昏迷
昏迷是未能均匀地放大离轴光。放大倍率随视场高度而变化。发生这种情况是因为由于光学表面的入射角不同,来自透镜相对两侧的光以不同的功率折射。
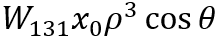
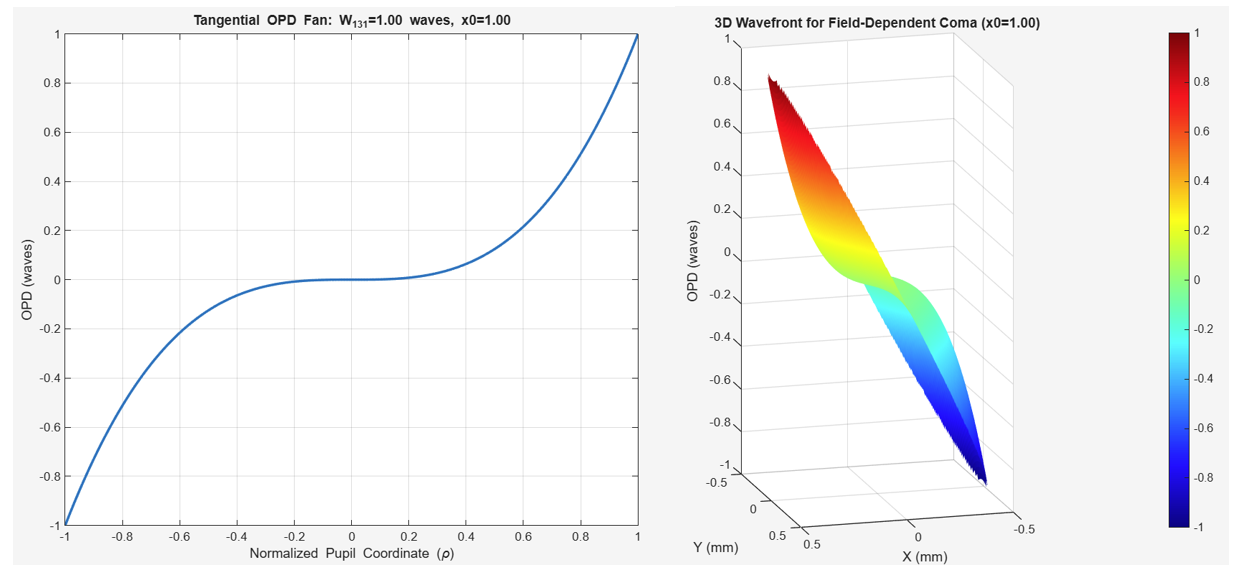
与球形内每个同心圆相关的模糊也可以在彗发中看到,但是每个圆都被推到与圆的直径成正比的方向。这是因为与球形不同,它有一个场相关项。由于瞳孔放大不对称,离轴点源会产生彗星形状的模糊。
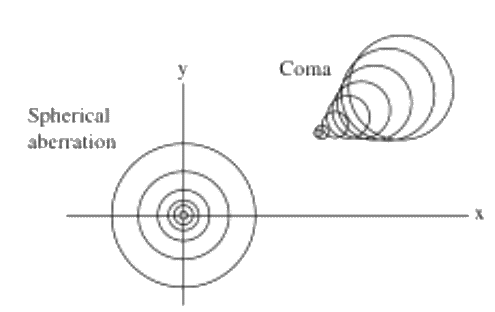
在 Zemax 中,彗发的相应作数是 COMA。
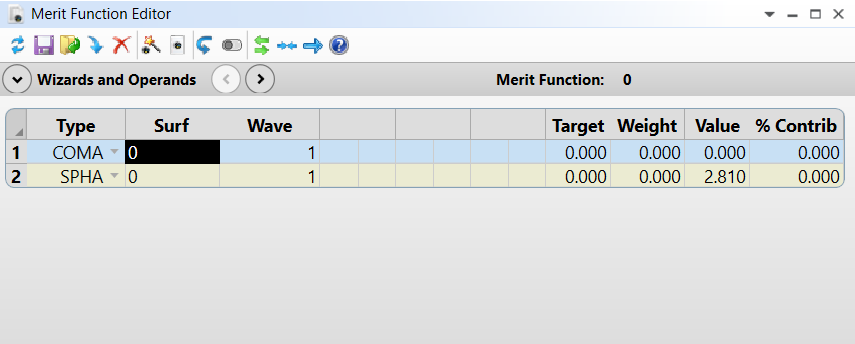
散光
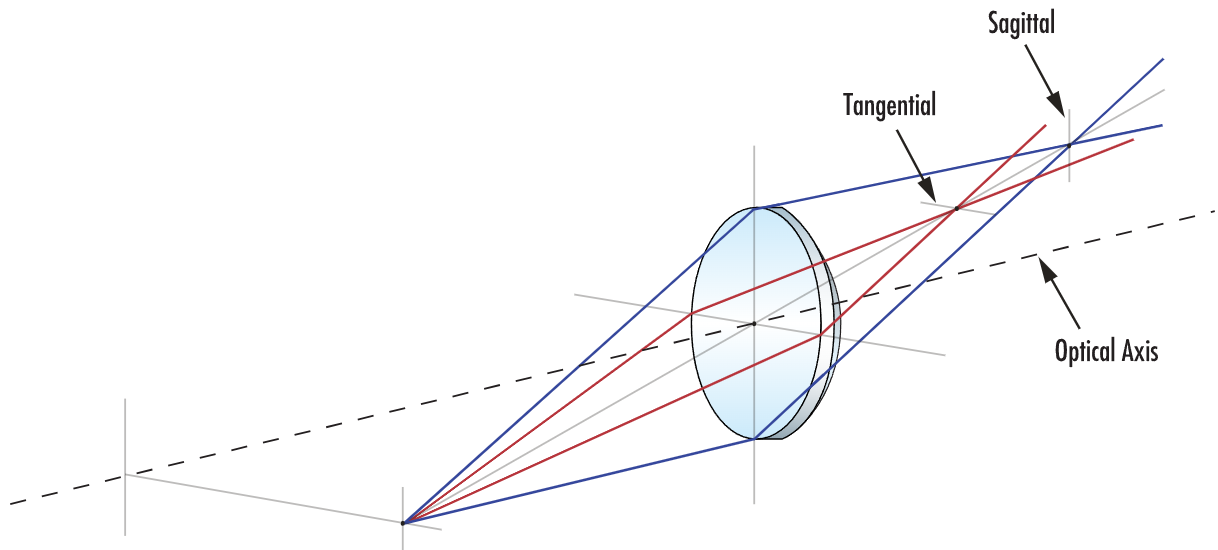
散光是最难矫正的像差。存在二次场依赖性,二次瞳孔依赖性。最简单的解释是,当透镜的焦点依赖于透镜表面的轴时,就会发生这种情况。换句话说,透镜表面具有与不同轴相关的不同功率。另一种看待这一点的方式是镜头同时存在对焦误差和放大误差。它可以是轴上像差或离轴像差,其中单个透镜具有两个垂直焦点,切向和矢状射线。
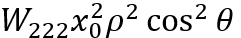
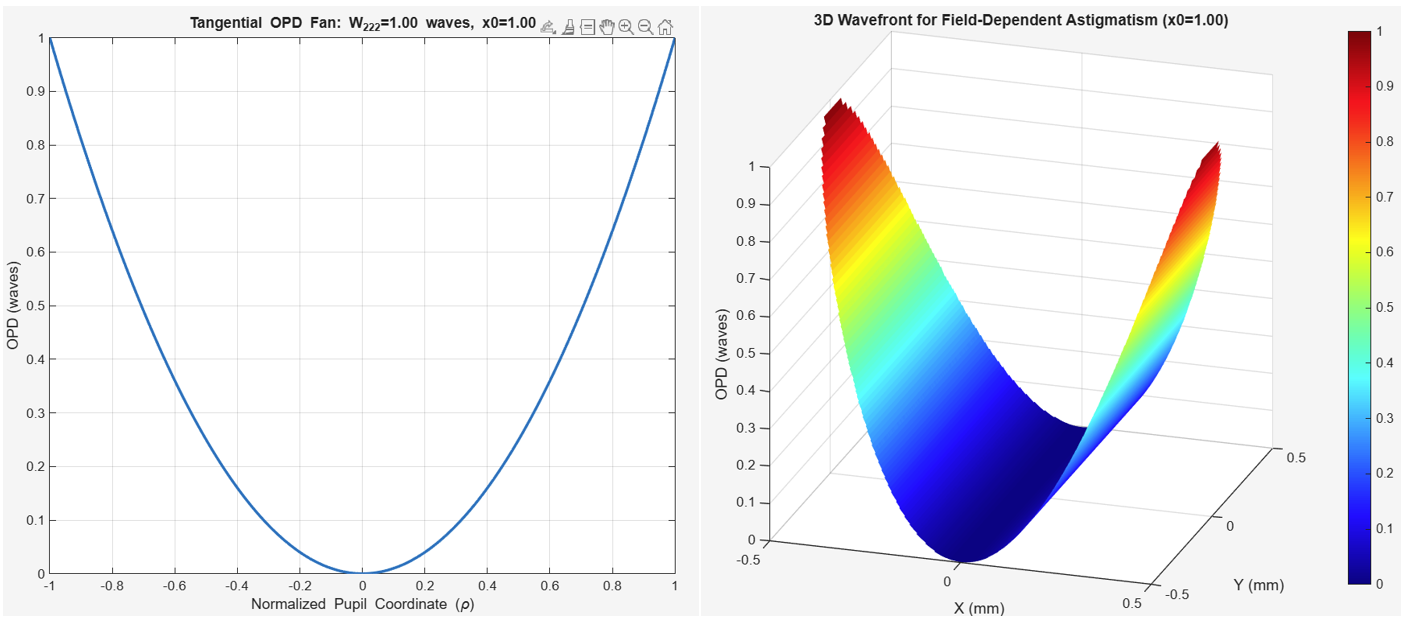
从光线追踪图中看散光很复杂,因为切向和矢状依赖性有两个病灶。瞳孔项由二次余弦项调制,该项在数学上给出了切向面和矢状面的不同结果。

在 Zemax 中,散光的相应作数是 ASTI。
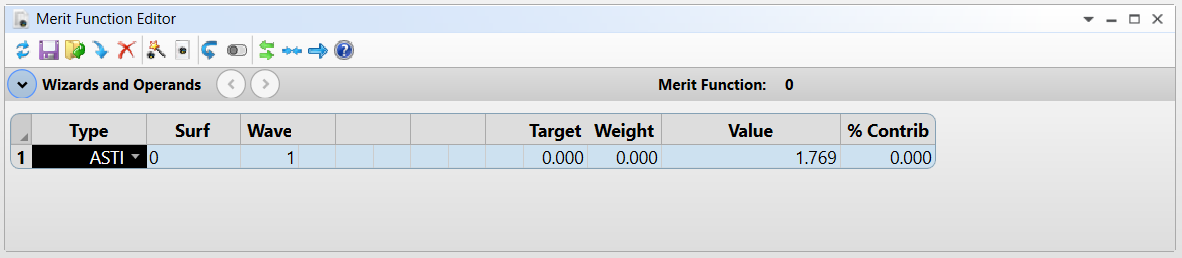
场曲率
视场曲率与散焦具有相同的瞳孔依赖性,但随视场高度呈二次方变化。这是无法将整个图像聚焦在单个平面上。相反,焦平面是一个类似于碗的抛物面,称为曲率的佩茨瓦尔曲面。即使散光被校正,各个视场点的锐焦也位于弯曲的 Petzval 曲面上,而不是平面图像平面上。这种像差是任何具有光功率的镜头系统所固有的,并且需要一个场透镜来压平该聚焦表面。
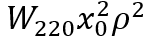
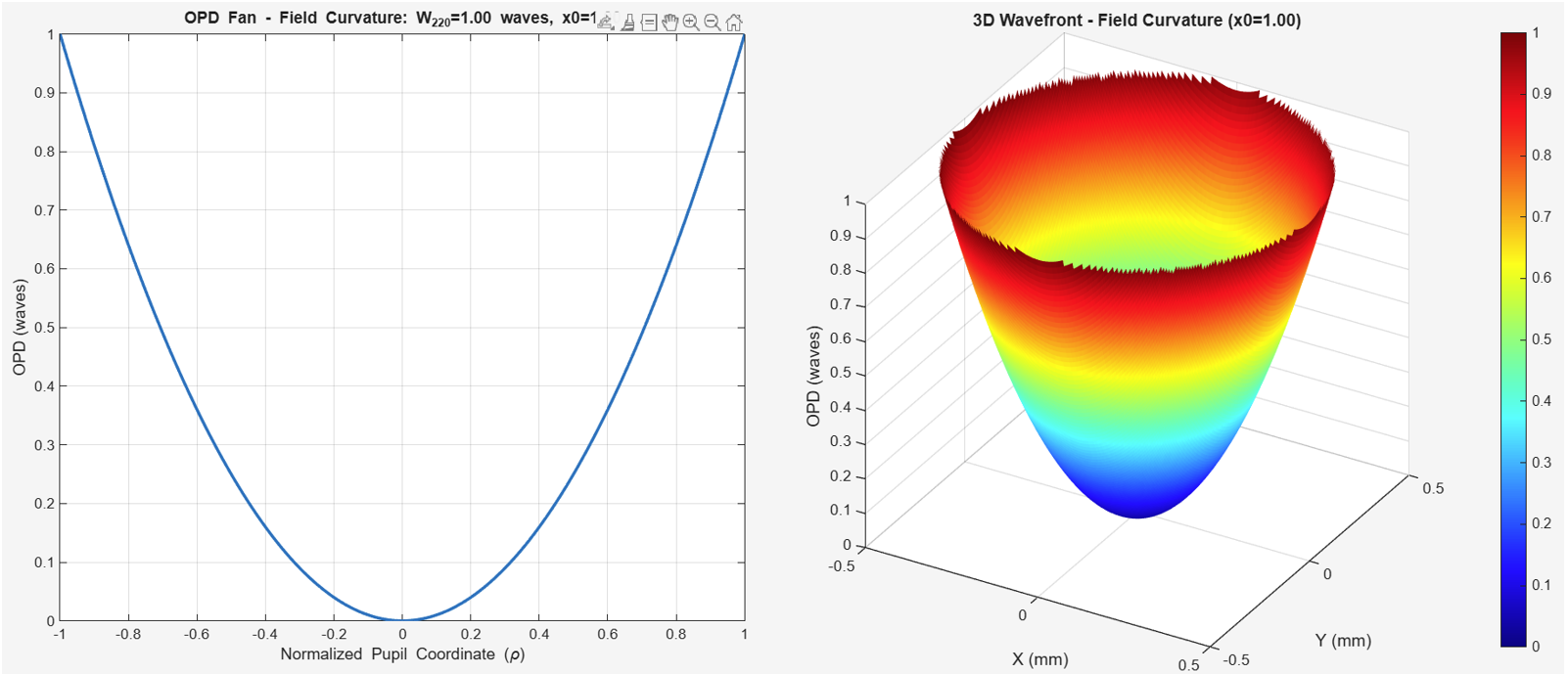
场曲率与散光直接相关,但它不受余弦项的调节。这是晶状体系统无法同时聚焦瞳孔中的所有视场和光线。
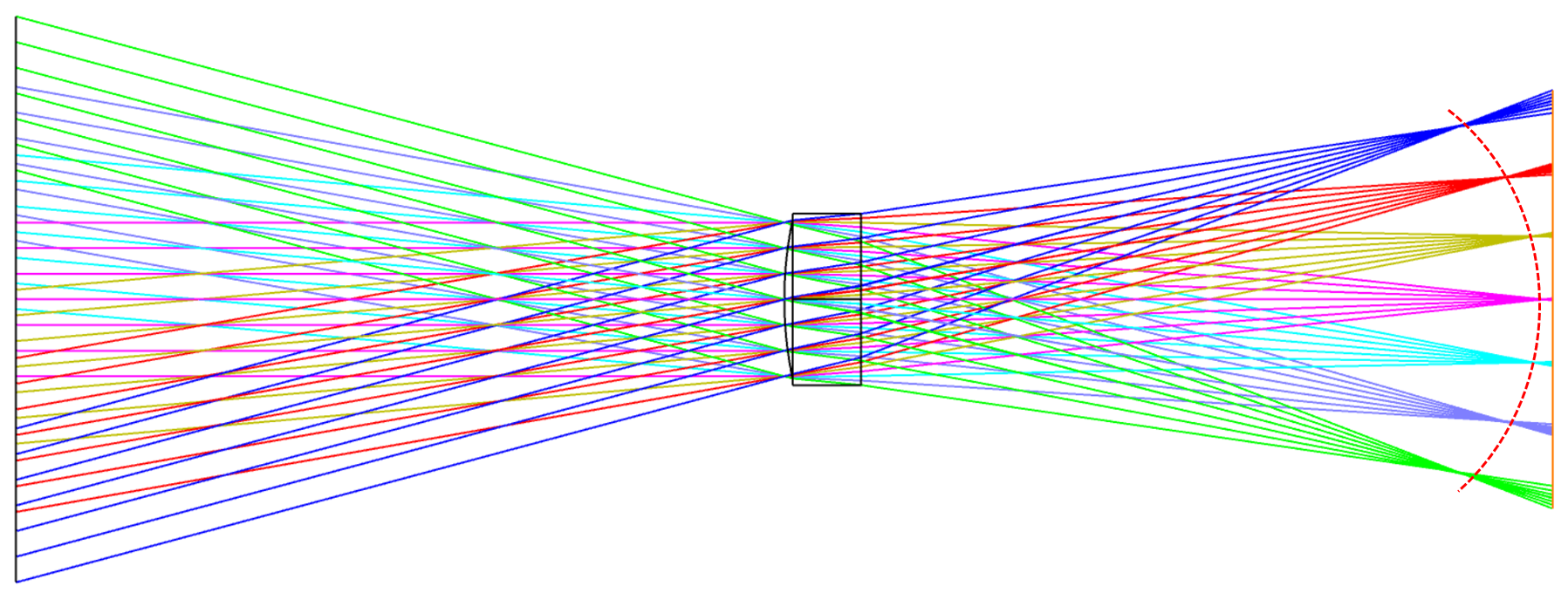
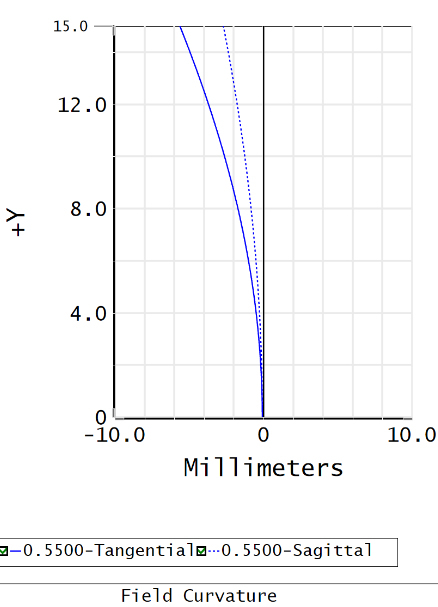
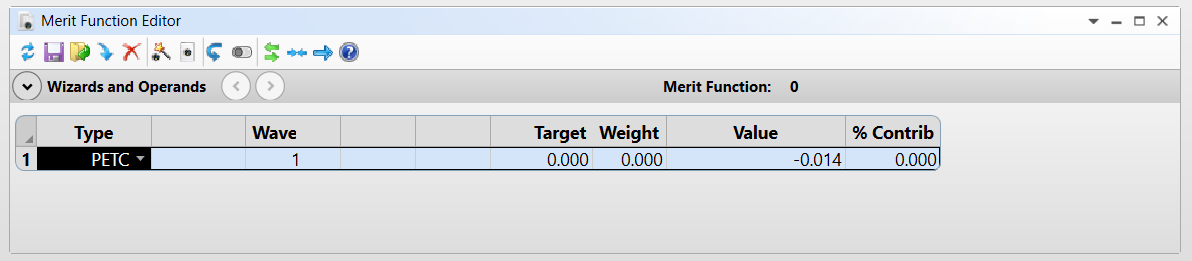
在 Zemax 中,场曲率的相应作数是 PETC。
失真
失真是指无法在整个视场上均匀放大图像。图像中的每个光线点都与图像位置的立方体成比例地偏离焦点。可以看作是“针垫或桶”,它更多的是形状的扭曲,而不是点的模糊。使用场展平器进行校正。
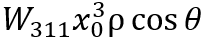
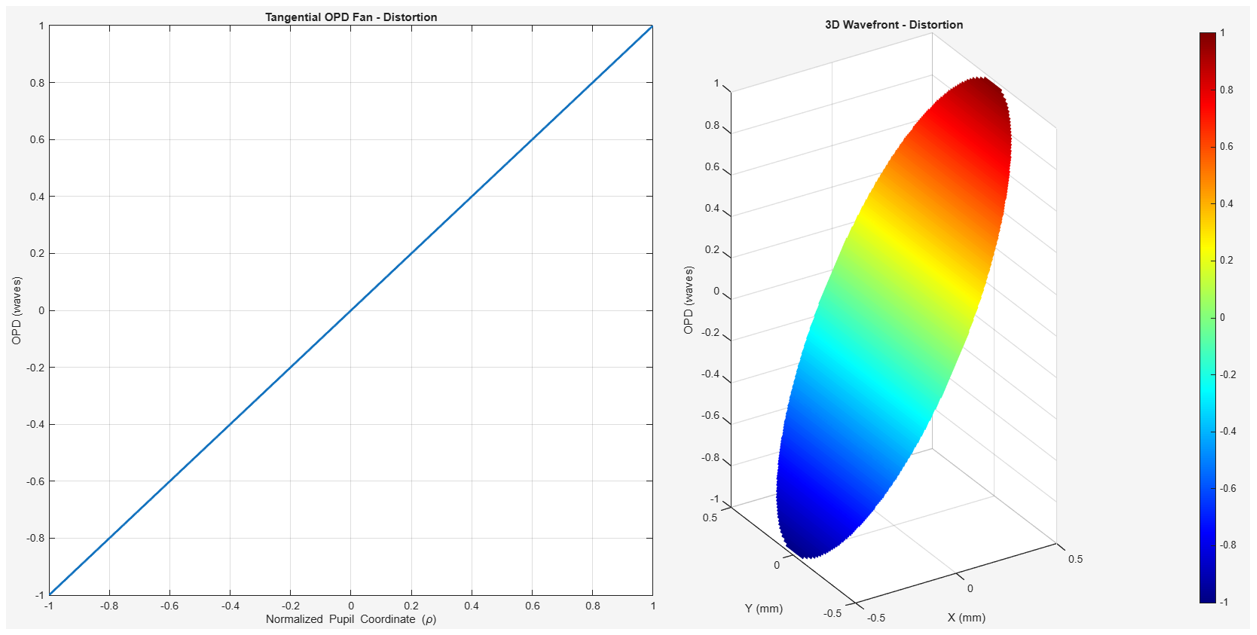

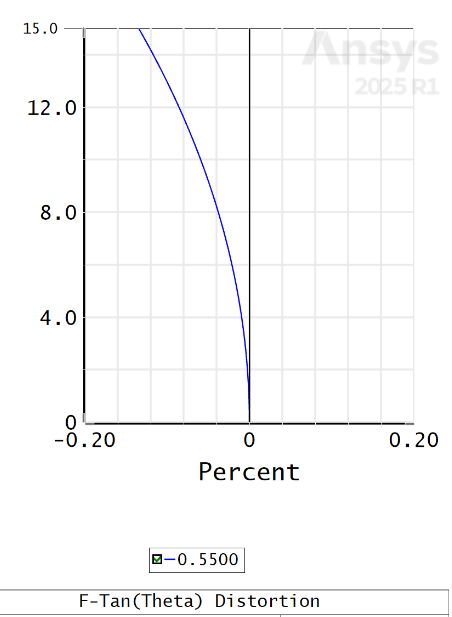
在 Zemax 中,失真对应的作数是 DIST。