当前位置：首页 > news >正文

【数据结构与算法】单调队列的定义和运用

news 2025/8/24 9:43:30

概述

单调队列算法基于双端队列。

关于 队列和双端队列 的知识，可以参考这里：

【C++】STL数据结构算法3—队列

下面重点看一道例题：

定义引入- - -例题：P1886 滑动窗口 /【模板】单调队列

传送门：P1886 滑动窗口 /【模板】单调队列 - 洛谷

题目大意

给定长度为 $n$ 的数列 $a$ 以及正整数 $k$

现有一个长度为 $k$ 的区间正在滑动

（初始为 $[1, k]$ ，最后滑动至 $[n - k + 1, n]$ ）

求每次滑动过后区间内数的最大值和最小值

（可以看原题的图，很容易理解）

数据范围

对于 100% 的数据， $1≤k≤n≤106,ai∈[−231,231)1\leq k \leq n \leq 10^6, a_i \in [-2^{31}, 2^{31})$

思路详解

暴力 $O(n^2)$

首先很容易想到暴力：直接枚举左端点 $l$ , 再遍历计算区间 $[l, l + k - 1] 内的最值$

由于代码太过基础，这里就暂且不贴出了
（~~绝对不是因为懒得写~~）

其它数据结构做法 $O (n l o g n)$

看到这种区间查询的题目，学过线段树/分块算法的朋友们可能就跃跃欲试了（

的确，我们可以建一颗线段树，写一个函数 $query⁡(l,r)\operatorname {query}(l,r)$ 计算区间最小值和最大值

确实可能能过，但代码量实在是太大了啊……（常数也很大）实在是不推荐

单调队列 $O (n)$

我们可以先只考虑求一个最值（例如求最大值）的做法：

由于只要求求最大值，显然易得：其它的非最大值的数都是无用的

由于滑动窗口有一定的范围，所以超出区间长度的数也是无用的

形象化地说，如果一个数比你的时效长（在后面的数能更长久地产生贡献），数值还比你大，那你就可以光荣“退休”了

那么我们可以考虑正序枚举数列，建一个双端队列，每次弹出队头超出使用时限的元素和队尾比当前元素小的元素。可以证明，当前队头的元素所对应的数组值一定是最大值！

（注意，为了判断时效，队列里要存数组元素的下标！！）

例如，对于数组 $[3, 6, 7, 5, 5, 5]$ ， $k = 3$ ：

首先队列依次进入 $1$ ，相安无事，不输出答案（因为 $1 < 3$ ）

接着队中欲新进入一个元素 $2$ 。检验时发现： $a_2 > a_1$ ，也就是说，在 $1$ 这个位置的数不仅比它早进入（更容易失效），还比它的值更小！于是我们弹出原先队尾的1，队列变为 $[2]$ ，同理不输出答案。

而后插入 $3, 4$ ，相安无事（虽然值比较小，但时效长，可能被用上）队列变为 $[2, 3, 4]$ ，答案为 $a_2=6$

当插入 $5$ 时，队尾自然是相安无事。但我们发现，当前的区间是 $[3, 5]$ ，队头的 $2$ 已经失效，不能参与计算了！于是，我们弹出 $2$ ，队列变为 $[3, 4, 5]$ ，答案为 $a_3=5$

以此类推，我们便能证明这个方法的正确性和时间复杂度的合理性。

至于最小值，只需要将弹出队尾的条件稍微修改即可（见代码）

AC代码

#include<iostream>
#include<queue>
using namespace std;
#define MaxN 1000005
#define For(i, j, k) for(int i = j; i <= k; i++)int n, k;
int a[MaxN];int main()
{cin >> n >> k;For(i, 1, n) cin >> a[i];deque<int> q;For(i, 1, n){while(!q.empty() && i-q.front()+1 > k) q.pop_front();while(!q.empty() && a[q.back()] > a[i]) q.pop_back();q.push_back(i);if(i >= k) cout << a[q.front()] << ' ';}cout << endl;q.clear();For(i, 1, n){while(!q.empty() && i-q.front()+1 > k) q.pop_front();while(!q.empty() && a[q.back()] < a[i]) q.pop_back();q.push_back(i);if(i >= k) cout << a[q.front()] << ' ';}cout << endl;return 0;
}

进阶运用- - P2698 Flowerpot S

传送门：P2698 [USACO12MAR] Flowerpot S - 洛谷

【题目描述】

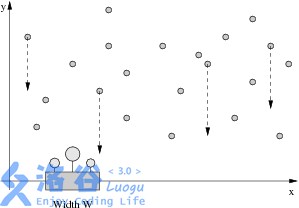
老板需要你帮忙浇花。给出 $N$ 滴水的坐标， $(x, y)$ 表示水滴最初的坐标。

每滴水均以每秒 $1$ 个单位长度的速度下落。你需要把花盆放在 $x$ 轴上的某个位置，使得花盆接到第 $1$ 滴水与最后 $1$ 滴水之间的时间差至少为 $D$ 。

如果水滴落在 $x$ 轴上的位置与花盆的边沿对齐，也认为被接住。

给出 $N$ 滴水的坐标和时间差 $D$ ，请算出最小的花盆宽度 $W$ 。

如果无法构造出满足题意的花盆，则输出 $- 1$ 。

【数据范围】

$40%40\%$ 的数据： $\le N \le 1000$ ， $\le D \le 2000$ 。

$100%100\%$ 的数据： $\le N \le 10 ^ 5$ ， $\le D \le 10 ^ 6$ ， $0≤x,y≤1060\le x,y\le10^6$ 。

思路详解

我们发现，若花盆的宽度已经确定，

这就变成了一个经典的滑动窗口问题，我们只需要求出每个窗口的最大值与最小值，再做差即可。

而对于花盆的宽度，我们完全可以用 $O⁡(logxmax)\operatorname O(logx_{max})$ 的时间来二分

这样，总时间复杂度 $O⁡(nlogn)\operatorname O(nlogn)$ ，求得正解

注意：首先要对数组按 $x$ 值进行排序！

AC代码

#include<bits/stdc++.h>
using namespace std;
#define For(i, j, k) for(int i = j; i <= k; i++)
#define dFor(i, j, k)for(int i = j; i >= k; i--)
#define MaxN 100086
#define int long longstruct Node{int x, y;bool operator < (const Node a){		//按x值排序return x < a.x;}
}a[MaxN];
int n, D;bool check(int k){deque<int> q1, q2;		//q1存最大值，q2存最小值For(i, 1, n){while(!q1.empty() && a[i].x - a[q1.front()].x > k) q1.pop_front();while(!q1.empty() && a[i].y <= a[q1.back()].y) q1.pop_back();q1.push_back(i);while(!q2.empty() && a[i].x - a[q2.front()].x > k) q2.pop_front();while(!q2.empty() && a[i].y >= a[q2.back()].y) q2.pop_back();q2.push_back(i);//		cout << q1.front() << ' ' << q2.front() << endl;if(a[q2.front()].y - a[q1.front()].y >= D) return 1;}return 0;
}signed main()
{cin >> n >> D;For(i, 1, n){cin >> a[i].x >> a[i].y;}sort(a+1, a+1+n);int l = 1, r = 10000086;while(l <= r){int mid = (l + r) / 2;if(check(mid)) r = mid - 1;else l = mid + 1;}if(l >= 10000000) cout << -1;else cout << l << endl;return 0;
}