【数据结构入门】二叉树(2)
目录
1.二叉树遍历顺序
1.1 前序(先根)遍历
1.2 中序(中根)遍历
1.3 后序(后根)遍历
1.4 层序遍历
1.5 深度优先遍历&广度优先遍历
2.二叉树的遍历
2.1 前根遍历(递归)
2.1.1 多路递归分析
2.1.2 OJ题目:前序遍历
2.1.3 OJ题目:单值二叉树
2.2 中根后根遍历(递归)
3. 二叉树的节点数量
4. 求二叉树叶子结点数量
5. 求二叉树深度
6.OJ:翻转二叉树
7.相同的树
8.另一个树的子树
1.二叉树遍历顺序
对于任意一个链式二叉树而言,可以将其看成三部分:根结点、左子树、右子树。
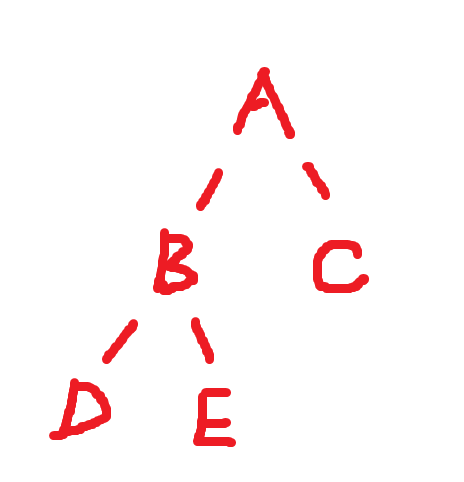
1.1 前序(先根)遍历
先遍历根节点,再遍历左节点,再遍历右节点。对于上图而言的遍历顺序为,A->B->D->E->C;
1.2 中序(中根)遍历
先遍历左节点,再遍历根结点,最后遍历右节点。对于上图而言的遍历顺序为,D->B->E->A->C;
1.3 后序(后根)遍历
先遍历左节点,再遍历右节点,最后遍历根结点。对于上图而言的遍历顺序为,D->E->B->C->A
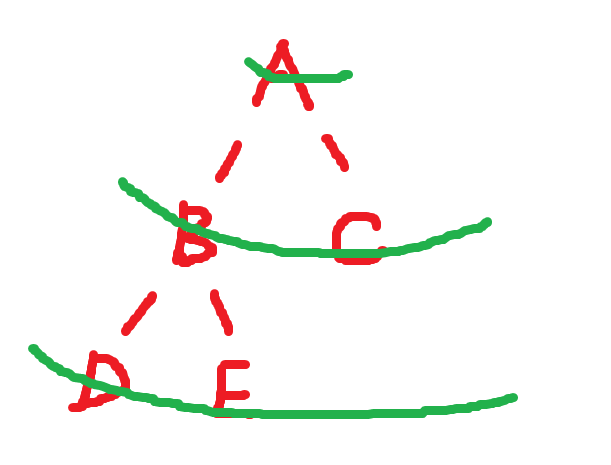
1.4 层序遍历
顾名思义按照一层一层来遍历所有的节点,A->B->C->D->E ,层序遍历可以用来判断是否是完全二叉树,因为如果将NULL节点打印出来的话,其实可以发现A->B->C->D->E NULL NULL NULL NULL NULL NULL
有效节点和空节点其实是分开的,这就可以判断是否是完全二叉树。
1.5 深度优先遍历&广度优先遍历
深度优先可以理解先朝着深处遍历,实在不能遍历,再进行回溯,例如前中后序遍历;
广度优先可以理解为以跟为中心点,一层一层往外扩张,层序遍历就是广度优先遍历。
2.二叉树的遍历
2.1 前根遍历(递归)

想要遍历以上的二叉树,我们可以使用上面介绍的遍历方法,由于树的结构就是天然的递归结构,那么我们可以使用递归方法来遍历树。
首先需要创建一个二叉树的结构体,该结构体需要左子树指针右子树指针以及当前节点存放的数据。
对于先根遍历,对于每一个节点来说都是先打印根结点再打印左子树再打印右子树,所以函数进入之后,直接打印根结点,递归调用自己的左子树和右子树,如果当前节点为空,那么说明已经到了叶子结点,需要进行函数的回退。
typedef struct BinaryTreeNode
{dataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BinaryTreeNode;// 遍历
void PreOrder(BinaryTreeNode* root)
{if (root == NULL){return;}// 先根printf("%c ", root->data);PreOrder(root->left);PreOrder(root->right);
}// 创建二叉树节点
BinaryTreeNode* CreateNode(char x)
{BinaryTreeNode* ret = (BinaryTreeNode*)malloc(sizeof(BinaryTreeNode));ret->data = x;ret->left = NULL;ret->right = NULL;return ret;
}// 求二叉树的大小int main()
{BinaryTreeNode* A = CreateNode('A');BinaryTreeNode* B = CreateNode('B');BinaryTreeNode* C = CreateNode('C');BinaryTreeNode* D = CreateNode('D');BinaryTreeNode* E = CreateNode('E');A->left = B;A->right = C;B->left = D;B->right = E;PreOrder(A);
}
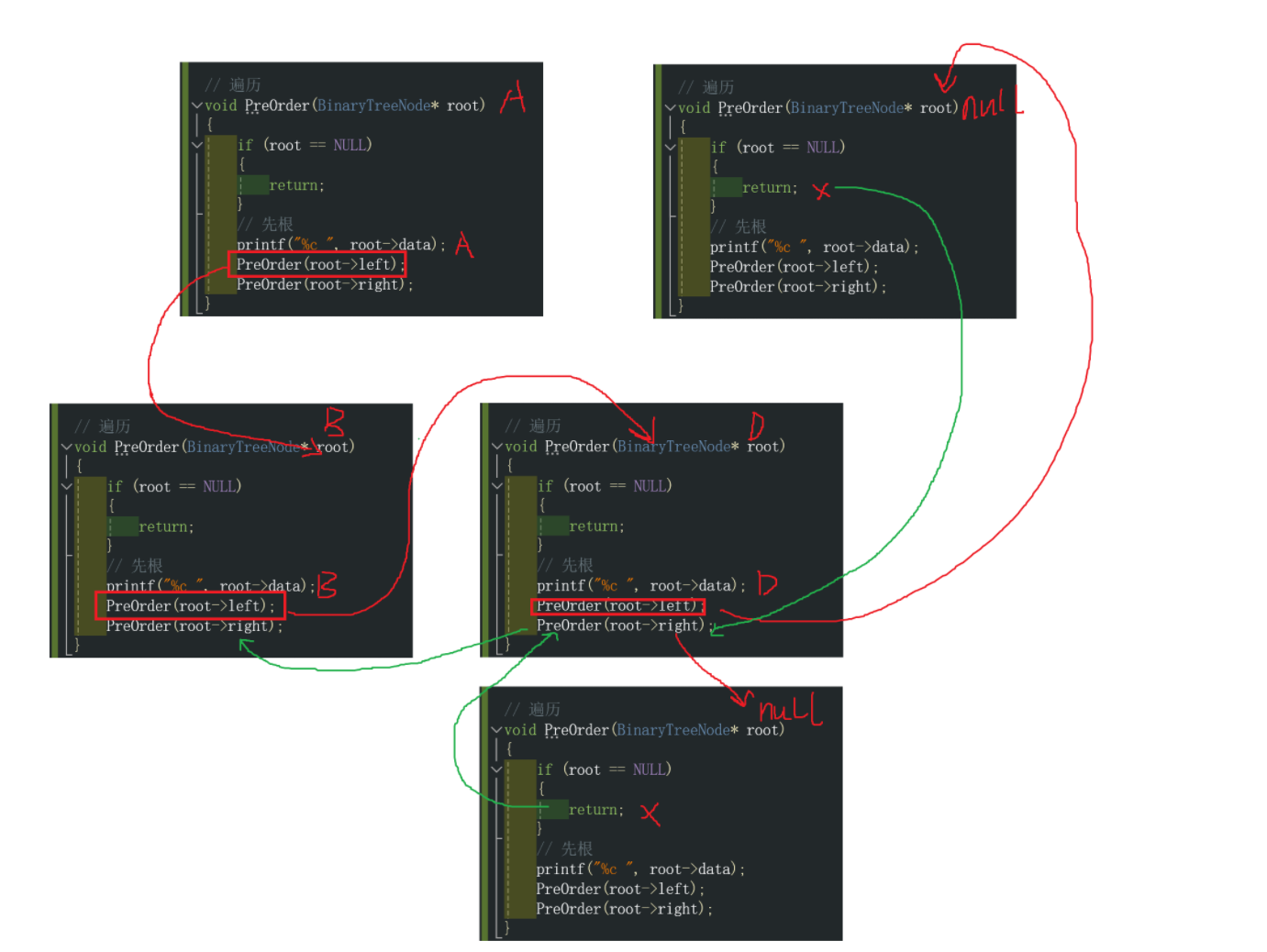
2.1.1 多路递归分析
我们简单地对上面这个先根遍历进行展开,首先节点A进入函数,打印A节点,调用A的左子树,将B作为新函数的root节点,打印B,将B的左子树作为新函数的根结点,打印D,将D的左子树作为根节点,判断为空那么函数就返回上一层调用函数的位置,继续执行将B的右子树传入函数,打印B的右子树E,将B的左子树作为函数的参数调用,打印D,将D的左子树作为参数调用函数,由于D的左孩子是NULL,此时函数直接返回到上一层,将D的右孩子作为参数进行调用,此时D的右孩子是NULL,继续返回上一层,发现上一层函数执行完毕,那么就继续调用根为B的节点的右孩子的递归,此时B的右孩子是E,打印E,将E的左右孩子作为参数进行递归调用,由于均是NULL,所以直接返回,最后B作为根节点的函数已经调用完毕,最后再调用以A为节点的函数,此时函数执行到了A节点的右孩子,最终打印C,以及C的左右孩子均为NULL,所以直接返回。
2.1.2 OJ题目:前序遍历
二叉树的前序遍历
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
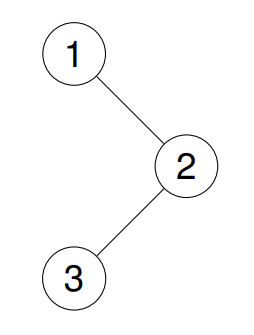
输入:root = [1,null,2,3]
输出:[1,2,3]
解释:
这道题目本身的逻辑不难,需要思考的是,如何将本该输出的操作转换为存入数组,首先需要传入一个数组,一个下标的指针,这里传入指针是因为,下标始终贯穿整个递归结构,不能被销毁,需要一直存在;
当将i下标的位置的元素赋值以后,需要立刻将下标++,再进行递归调用左子树和右子树。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/typedef struct TreeNode TreeNode;int treeSize(TreeNode* root){if(root == NULL){return 0;}else{return 1 + treeSize(root->left) + treeSize(root->right);}}void preOrder(TreeNode* root,int* arr, int* i)
{if(root == NULL){return;}// 放入数组arr[(*i)] = root->val; ++(*i);preOrder(root->left,arr,i);preOrder(root->right,arr,i);}int* preorderTraversal(struct TreeNode* root, int* returnSize) {int* ret = (int*) malloc(sizeof(int)*treeSize(root));int i = 0;preOrder(root,ret,&i);*returnSize = treeSize(root);return ret;
}2.1.3 OJ题目:单值二叉树
果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false。
示例 1:
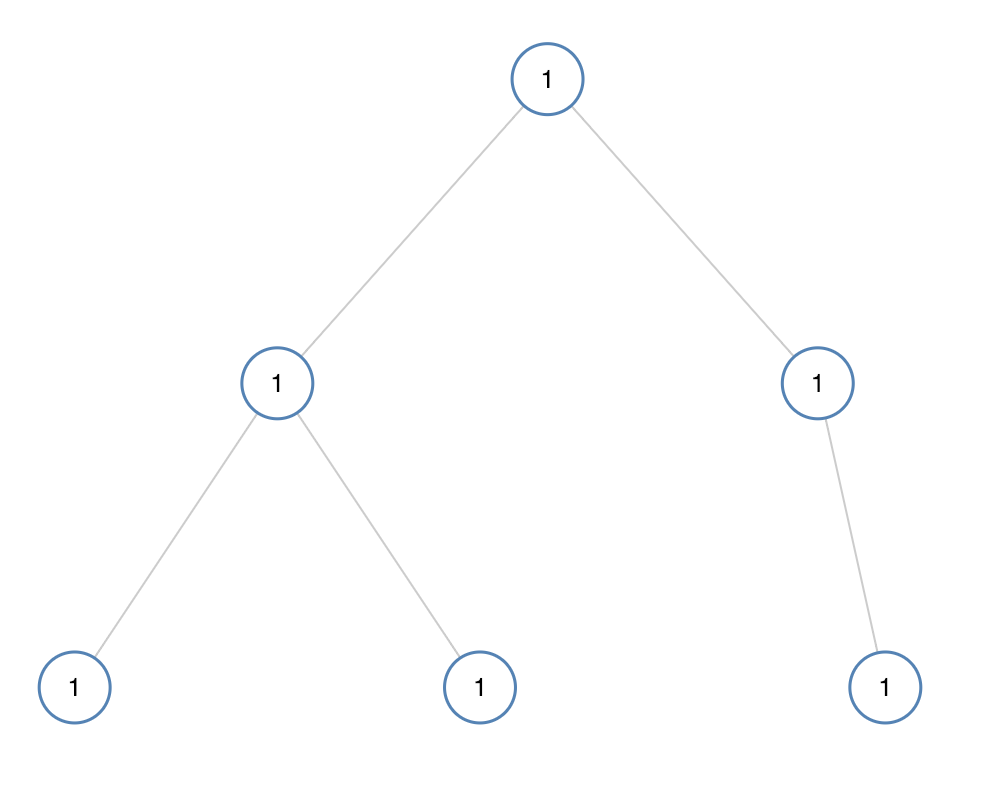
输入:[1,1,1,1,1,null,1] 输出:true
先考虑当前树,在考虑左右子树。
首先判断单个节点为空,那么说明为真,因为空节点其实不影响判断单值。
若根结点不为空,在左节点不为空的情况下,如果左节点的值和根结点的值不等,说明不是单值,返回false;
右节点同理;
最后判断左子树和右子树如果同时是true,说明左右子树都是单值,若有一个为false说明就不是单值。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/typedef struct TreeNode TreeNode;
bool isUnivalTree(struct TreeNode* root) {// 只有一个节点是单值二叉树if(root == NULL){return true;}// 当左节点和根结点不相等返回假if(root->left != NULL && root->val != root->left->val){return false;}// 当右节点和根结点不相等返回假if(root->right!= NULL && root->val != root->right->val){return false;}// 左子树和右子树return isUnivalTree(root->left) && isUnivalTree(root->right);}2.2 中根后根遍历(递归)
如果理解了前序遍历,那么中根遍历其实就是先访问左子树再打印根,访问右子树。
// 中序遍历
void InOrder(BinaryTreeNode* root)
{if (root == NULL){return;}PreOrder(root->left);printf("%c ", root->data);PreOrder(root->right);
}// 后序遍历
void PostOrder(BinaryTreeNode* root)
{if (root == NULL){return;}PreOrder(root->left);PreOrder(root->right);printf("%c ", root->data);
}3. 二叉树的节点数量
同样可以使用递归来求,如果当前节点是NULL,那么就直接结束该函数,不然就将size++,这里需要注意的是由于递归调用函数是栈,在函数内定义size,每次函数结束的时候size会销毁,所以这里需要把size设置成静态局部变量。
++完size之后需要遍历左子树和右子树,这里遍历的顺序没有要求。
// 求二叉树的大小
int TreeSize(BinaryTreeNode* root)
{static int size = 0;if (root == NULL){return 0;}++size;// 遍历左右子树TreeSize(root->left);TreeSize(root->right);return size;
}这里有一个致命的问题,如果这个函数被调用多次,那么次数是会被累加计算的,因为函数执行结束的时候该变量是存储在静态区中,是不会被销毁的。
所以这里的size是由外界传入的,如果此节点非空那么size++,这样也会解决上述提到的问题。
// 求二叉树的大小
void TreeSize(BinaryTreeNode* root, int* size)
{if (root == NULL){return;}++(*size);// 遍历左右子树TreeSize(root->left, size);TreeSize(root->right, size);
}int main()
{BinaryTreeNode* A = CreateNode('A');BinaryTreeNode* B = CreateNode('B');BinaryTreeNode* C = CreateNode('C');BinaryTreeNode* D = CreateNode('D');BinaryTreeNode* E = CreateNode('E');A->left = B;A->right = C;B->left = D;B->right = E;//PreOrder(A);int size = 0;TreeSize(A, &size);printf("%d ", size);
}但是这种方法需要传入一个size,对于调用方法的人来说非常不友好,那么有没有一种方法,可以直接返回当前的根结点的二叉树节点数呢?
若节点为空,返回0,若不为空就返回1(本身)+左子树+右子树的节点数量。
// 求二叉树的大小
int TreeSize(BinaryTreeNode* root)
{if (root == NULL){return 0;}else{return 1 + TreeSize(root->left) + TreeSize(root->right);}
}4. 求二叉树叶子结点数量
首先使用递归来解决,判断当前节点是否为空节点,然后判断当前节点是否为叶子结点(左右子树为空),最后就是普通的节点,此时计算该叶子结点是左子树叶子结点+右子树叶子结点。
// 求二叉树叶子结点个数
int LeafSize(BinaryTreeNode* root)
{// 是空吗if (root == NULL) {return 0;}// 是叶子节点吗if (root->right == NULL && root->left == NULL) {return 1;}return LeafSize(root->left) + LeafSize(root->right);
}
5. 求二叉树深度
如果空节点,深度为0;除此以外,剩下的节点都按照左子树深度和右子树深度中最大的那一个再+1(本节点)计算。
// 二叉树的深度
int TreeDepth(BinaryTreeNode* root)
{// 如果空节点深度就是0if (root == NULL) {return 0;}int leftDepth = maxDepth(root->left);int rightDepth = maxDepth(root->right);return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}6.OJ:翻转二叉树
给定一棵二叉树的根节点 root,请左右翻转这棵二叉树,并返回其根节点。
示例 1:
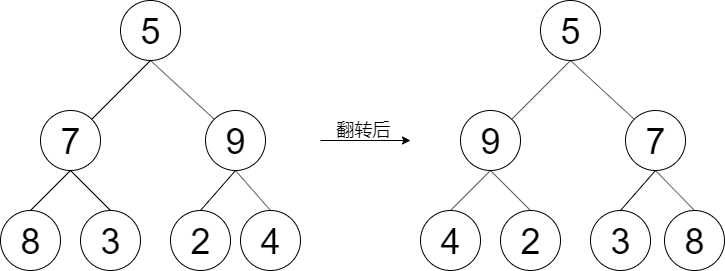
输入:root = [5,7,9,8,3,2,4] 输出:[5,9,7,4,2,3,8]
如果根结点为空,直接返回NULL,如果不为空就交换根结点的左右节点,应用在左子树和右子树上,最后返回根结点。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
struct TreeNode* flipTree(struct TreeNode* root) {if (root == NULL) {return NULL;}struct TreeNode* tmp = root->left;root->left = root->right;root->right = tmp;flipTree(root->left);flipTree(root->right);return root;
}还有一种解法:刚刚的解法是先处理根结点在处理左子树和右子树,属于前序遍历,那么可以先处理左右子树,在处理根结点。
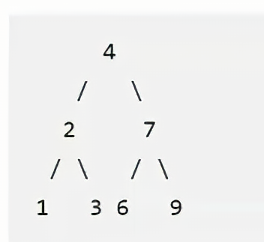
例如先将,2和7的子树进行翻转,最后将4的right连到2,4的left连接到7;
struct TreeNode* flipTree(struct TreeNode* root) {if (root == NULL) {return NULL;} else {struct TreeNode* tmp = root->right;root->right = flipTree(root->left);root->left = flipTree(tmp);return root;}
}7.相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
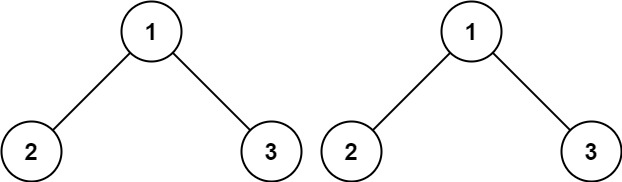
输入:p = [1,2,3], q = [1,2,3] 输出:true
首先如果两个节点都是空,那么说明完全是相同的,直接返回true;
若一个节点为空另一个节点不为空,说明两个节点结构不同,返回false;
若两个节点都不为空,并且值还不相等,说明这两个节点不相等,返回false;
最后判断左右子树为true的情况下返回true,否则false;
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {// 都是空也相等if (p == NULL && q == NULL) {return true;}// 结构不同if (p == NULL && q != NULL) {return false;}if (q == NULL && p != NULL) {return false;}// qp都不为空,值不同if (p->val != q->val) { //此时如果两个值相同依旧不能判断结果,因为没有判断左右子树,所以这里判断不相等的时候return false;} // 结构相同、值相同,判断左右子树return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}8.另一个树的子树
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:
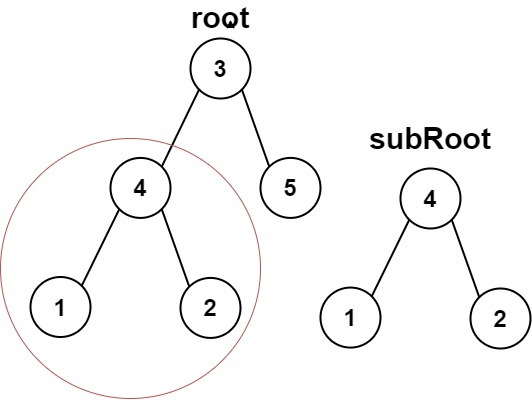
输入:root = [3,4,5,1,2], subRoot = [4,1,2] 输出:true
示例 2:
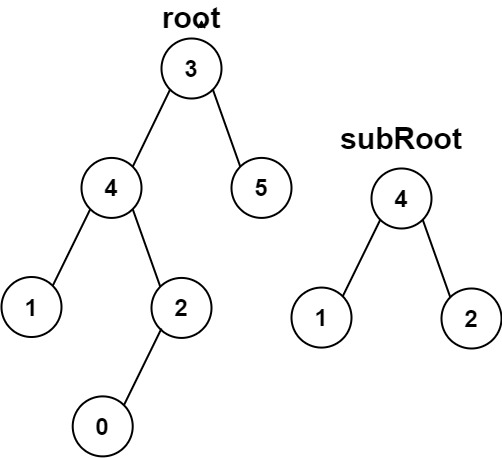
输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] 输出:false
从示例2可以得出,子树的定义是某一个子树到叶子结点与提供的子树完全相同,子树不能有子树。
首先需要判断主树为空,那么就不需要判断子树了,没有树是NULL的子树,返回false;
然后判断若两棵树如果是同一棵树(借助上一题的接口),那么就返回true;
如果没有找到,那么就去递归左子树,若左子树没找到,再递归右子树。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/bool isSameTree(struct TreeNode* p, struct TreeNode* q) {// 都是空也相等if (p == NULL && q == NULL) {return true;}// 结构不同if (p == NULL && q != NULL) {return false;}if (q == NULL && p != NULL) {return false;}// qp都不为空,值不同if (p->val != q->val) { //此时如果两个值相同依旧不能判断结果,因为没有判断左右子树,所以这里判断不相等的时候return false;} // 结构相同、值相同,判断左右子树return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {// 如果主树是空的,就不需要比了if(root == NULL){return false;}// 如果主树和子树比对上了,返回trueif(isSameTree(root,subRoot)){return true;}// 如果没找到,先去左子树找,左子树没找到去右子树return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}