院校机试刷题第二十三天|大精度整数运算、约瑟夫环

一、大精度整数运算

高精度加法

int：-2^31~2^31-1，为10^9数量级

long long：-2^63~2^63-1，为10^18数量级

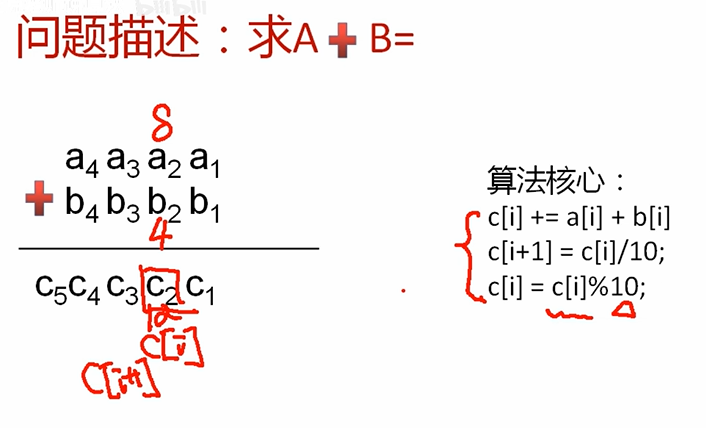
算法：

输入：以string类型输入两个大数

将string类型转换为int数组类型，注意string对应的下标和int对应的下标是相反的，例如输入123，string类型1对应的下标为0，int数组类型中1对应的下标为2，需要有一个倒置的过程。

执行两个数组相加的过程

删除前导0

输出相加之后的结果

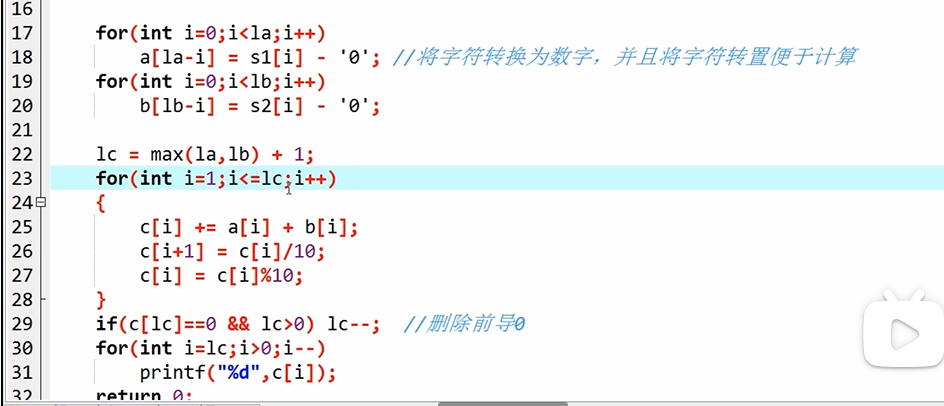
高精度减法

算法：

仍然是先按照string类型输入，然后转换为int数组。

运算时，如果a < b，将两者交换位置。可以在string类型的时候就进行比较，先看两者的长度，长度更长的那个数字更大；如果两者一样长，依次比较两者高位（实际上是string的低位）谁大

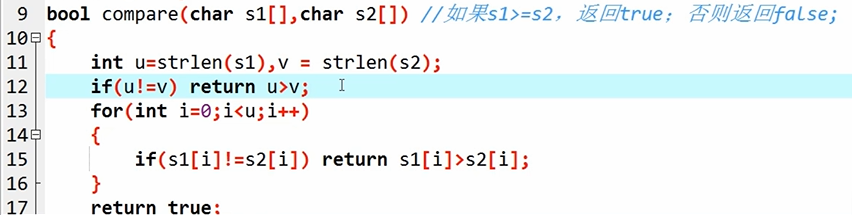
如果a[i] < b[i]，那么就借位，如上图所示

去掉前导零

输出

高精度乘法

算法：

输入：string类型输入，转换为int数组

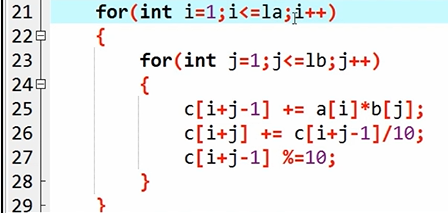
运算过程：两层for循环依次遍历a和b的所有元素，并对c的元素进行赋值

去除前导0，之前给结果准备的c数组长度应该是两者长度之和

输出

高精度除法

高精度除以低精度

实际上是不断进行除法，然后取余数的过程，借助低精度运算符 / 和 % 来进行

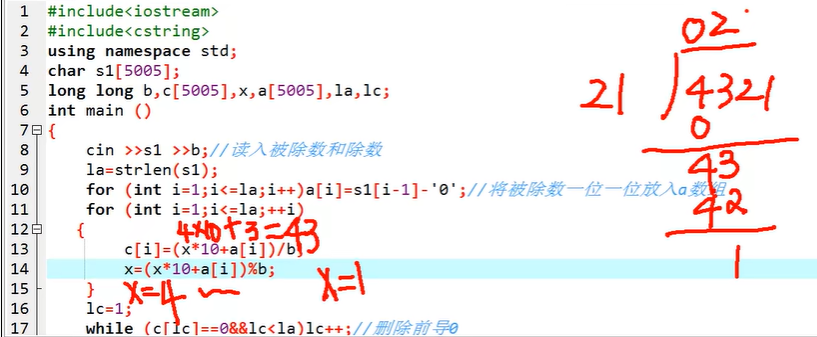
输入：string类型输入高精度整数，转换为int数组的时候不需要倒置，因为除法就是从最高位先开始的

运算：从最高位开始逐位试商、取余，得到余数之后和下一位拼起来再次试商取余，直到将高精度整数所有位数都遍历结束。

删除前导0

输出

（x的初始值为0，用来记录余数）

高精度除以高精度

用高精度减法模拟高精度除法，减了几次之后，如果这个数被减到了比之前的被减数少了一位，那么就算一次除法，这一位的商就是减法进行了的次数。一直这样，直到减得的数比除数小，那么就结束。

在相减的过程中，需要首先将除数进行右侧补零，使得减数和被减数长度相等，补的位数为商的下标，例如4这位商，是c[3]，那么123需要在后面补3个0。（如果是商的下标从1开始算那补的位数就是商的下标-1）

算法

相减的话，结果的位数先设定为被除数位数 - 除数位数 + 1即可。

二、约瑟夫环

1.问题描述

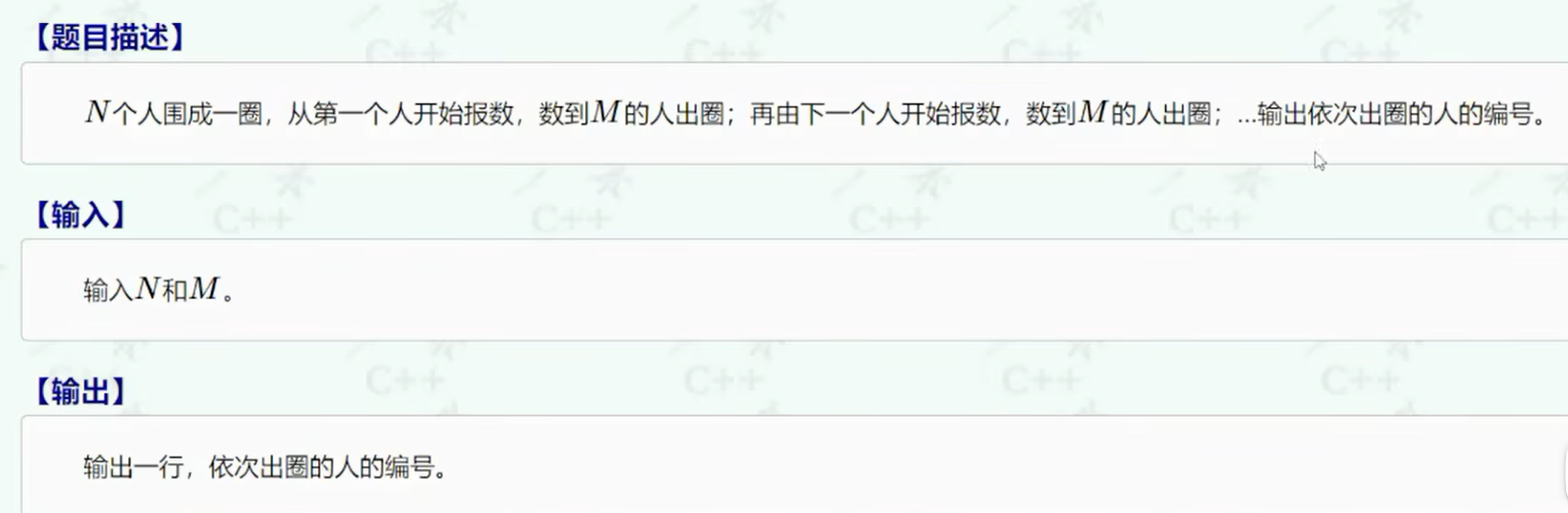
2.循环链表模拟

循环链表模拟：将所有的n个数存入循环链表中，head指向第一个节点，ptr遍历所有的链表节点，front指向ptr的前一个节点，cnt用来数遍历到第几个节点了，数组result存储所有的出队的节点，伪代码如下图所示

#include <iostream>
using namespace std;struct Node {int data;Node* next;Node(int x) : data(x), next(nullptr) {}
};int josephus(int n, int k) {if (n == 1) return 1;// 创建循环链表Node* head = new Node(1);Node* prev = head;for (int i = 2; i <= n; i++) {prev->next = new Node(i);prev = prev->next;}prev->next = head; // 形成环Node* curr = head;Node* prevNode = prev;while (curr->next != curr) { // 直到只剩一个人// 找到第k个节点for (int i = 1; i < k; i++) {prevNode = curr;curr = curr->next;}// 删除当前节点prevNode->next = curr->next;delete curr;curr = prevNode->next;}int result = curr->data;delete curr;return result;
}int main() {int n = 7, k = 3;cout << "The last remaining person is " << josephus(n, k) << endl;return 0;
}