当前位置： 首页 > news >正文

二叉树应用实践

news 2025/8/18 14:38:33

目录

单值二叉树（力扣）

代码实现：

核心逻辑：

相同的树

代码实现：

核心逻辑：

对称的树（由相同的树衍生）

代码实现：

核心逻辑：

另一棵树的子树

核心逻辑：

代码实现：

二叉树的前中后序遍历（以前为例）

代码实现：

核心逻辑：

注意：

二叉树遍历（牛客）：

代码实现：  

基本逻辑：

单值二叉树（力扣）

https://leetcode.cn/problems/univalued-binary-tree/description/

代码实现：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isUnivalTree(TreeNode* root) {if(root==NULL){return true;}if ((root->left != NULL && root->val != root->left->val) || (root->right != NULL && root->val != root->right->val)) {return false;
}return isUnivalTree(root->left)&&isUnivalTree(root->right);}
};

核心逻辑：

  1. 空树处理：如果根节点 root 为 NULL（空树），直接返回 true，因为空树可视为单值二叉树。
  2. 当前节点与子节点值的检查：
    • 若左子节点存在且其值与当前节点值不同，或者右子节点存在且其值与当前节点值不同，说明不是单值二叉树，返回 false。
  3. 递归检查子树：递归地检查左子树和右子树是否为单值二叉树，只有当左子树和右子树都为单值二叉树时，整个树才是单值二叉树，返回 true。

相同的树

https://leetcode.cn/problems/same-tree/description/

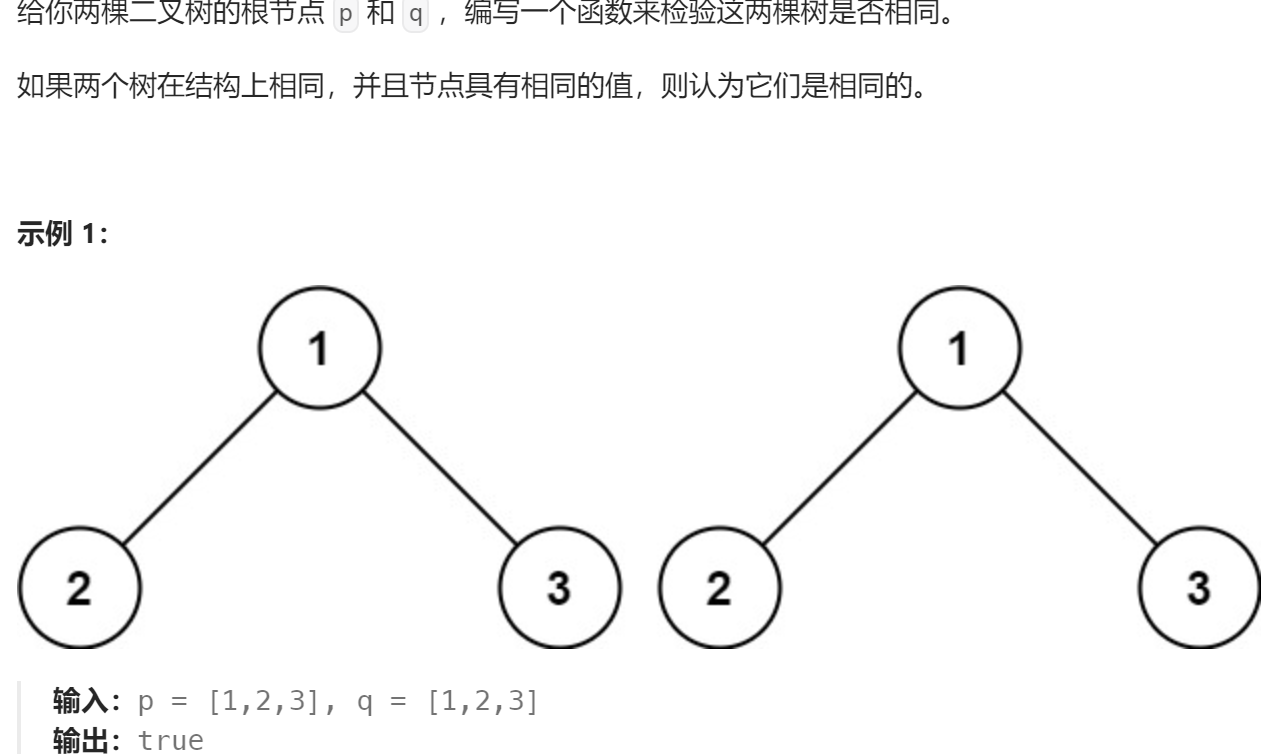
代码实现：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isSameTree(TreeNode* p, TreeNode* q) {if(p==NULL&&q==NULL){return true;}if(p==NULL||q==NULL){return false;}if(q->val!=p->val){return false;}return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);}
};

核心逻辑：

  1. 基础情况判断：

    • 如果两棵树的当前节点都为NULL（空），返回true（空树视为相同）
    • 如果其中一棵树的当前节点为NULL而另一棵不为NULL，返回false（结构不同）

  2. 节点值判断：

    • 如果当前节点的值不相等，返回false（值不同）

  3. 递归判断子树：

    • 递归判断左子树是否相同
    • 递归判断右子树是否相同
    • 只有左右子树都相同时，才返回true

对称的树（由相同的树衍生）

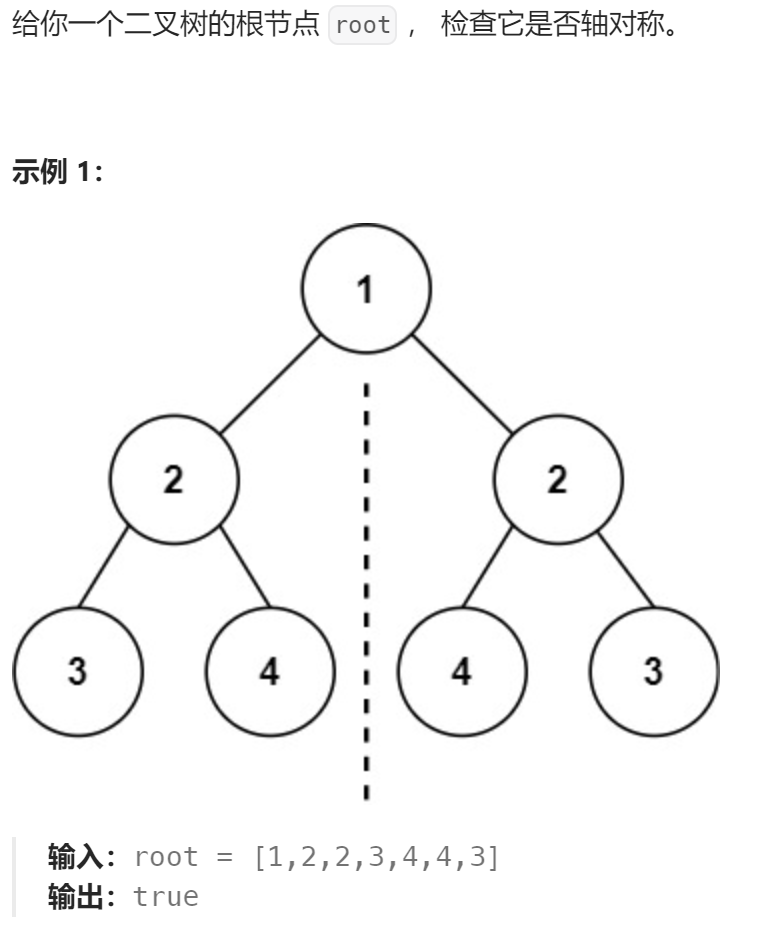
代码实现：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {if(p==NULL&&q==NULL){return true;}if(p==NULL||q==NULL){return false;}if(q->val!=p->val){return false;}return isSameTree(p->left,q->right)&&isSameTree(p->right,q->left);}bool isSymmetric(TreeNode* root) {return isSameTree(root->left,root->right);}
};

核心逻辑：

  1. 定义isSameTree函数的变种，比较规则改为：判断一棵树的左子树与另一棵树的右子树、一棵树的右子树与另一棵树的左子树是否相同。
  2. 在isSymmetric函数中，通过调用上述变种isSameTree，比较根节点的左子树和右子树是否满足对称条件，以此确定整棵树是否对称。

另一棵树的子树

https://leetcode.cn/problems/subtree-of-another-tree/description/

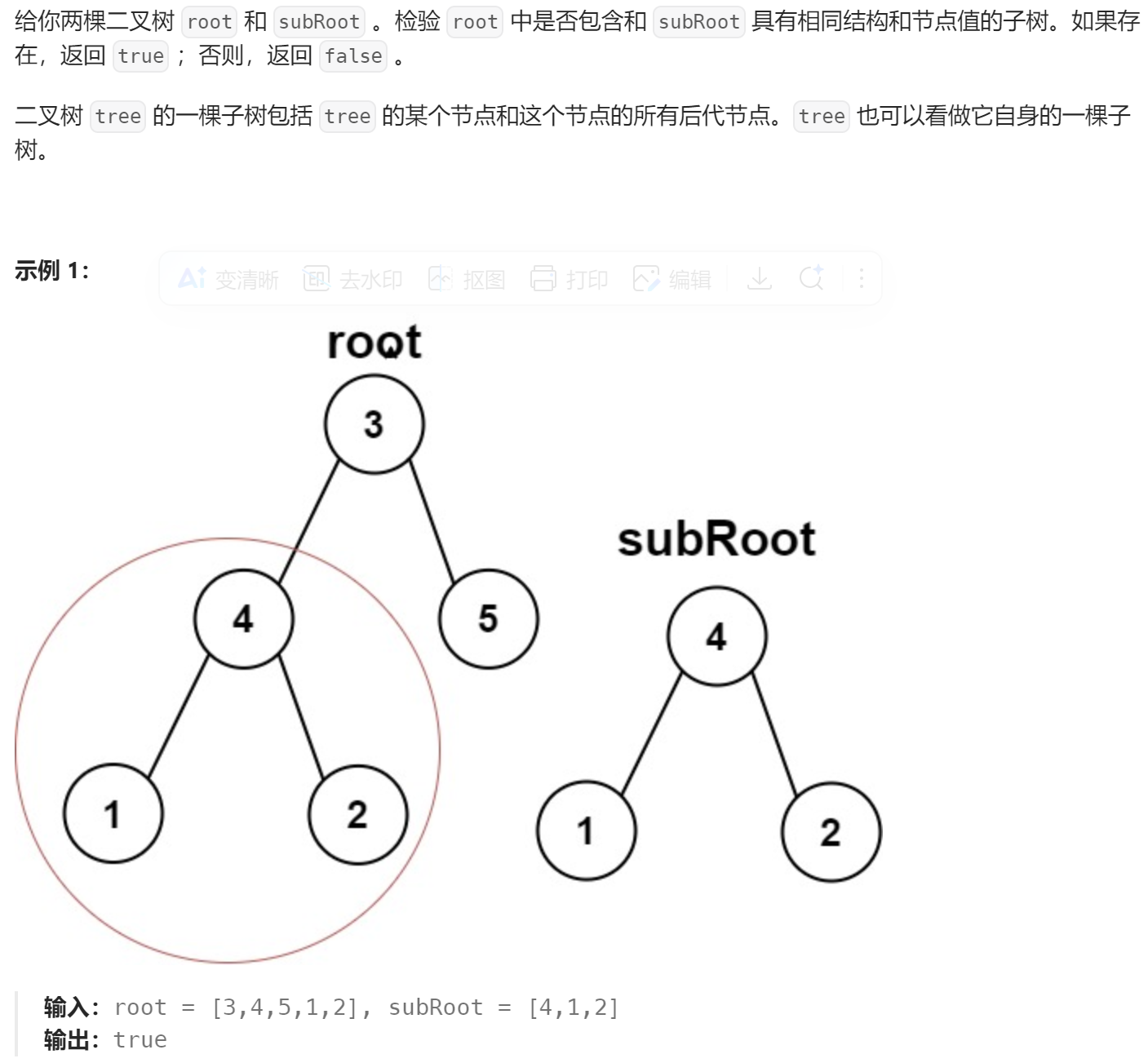
核心逻辑：

  1. 判断两棵树是否完全相同（isSameTree 函数）

    • 若两棵树的当前节点都为空，返回 true
    • 若其中一棵为空另一棵不为空，返回 false
    • 若节点值不同，返回 false
    • 递归检查左子树和右子树是否都相同

  2. 判断子树关系（isSubtree 函数）

    • 若主树 root 为空，返回 false（空树不可能包含非空子树）
    • 若当前节点开始的子树与 subRoot 相同，返回 true
    • 否则递归检查 root 的左子树或右子树是否包含 subRoot

代码实现：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {if(p==NULL&&q==NULL){return true;}if(p==NULL||q==NULL){return false;}if(q->val!=p->val){return false;}return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);}bool isSubtree(TreeNode* root, TreeNode* subRoot) {if(root==NULL){return false;}if(isSameTree(root,subRoot)){return true;}return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);}
};

二叉树的前中后序遍历（以前为例）

前序遍历：https://leetcode.cn/problems/binary-tree-preorder-traversal/description/

中序遍历：https://leetcode.cn/problems/binary-tree-inorder-traversal/description/

后序遍历：https://leetcode.cn/problems/binary-tree-postorder-traversal/description/

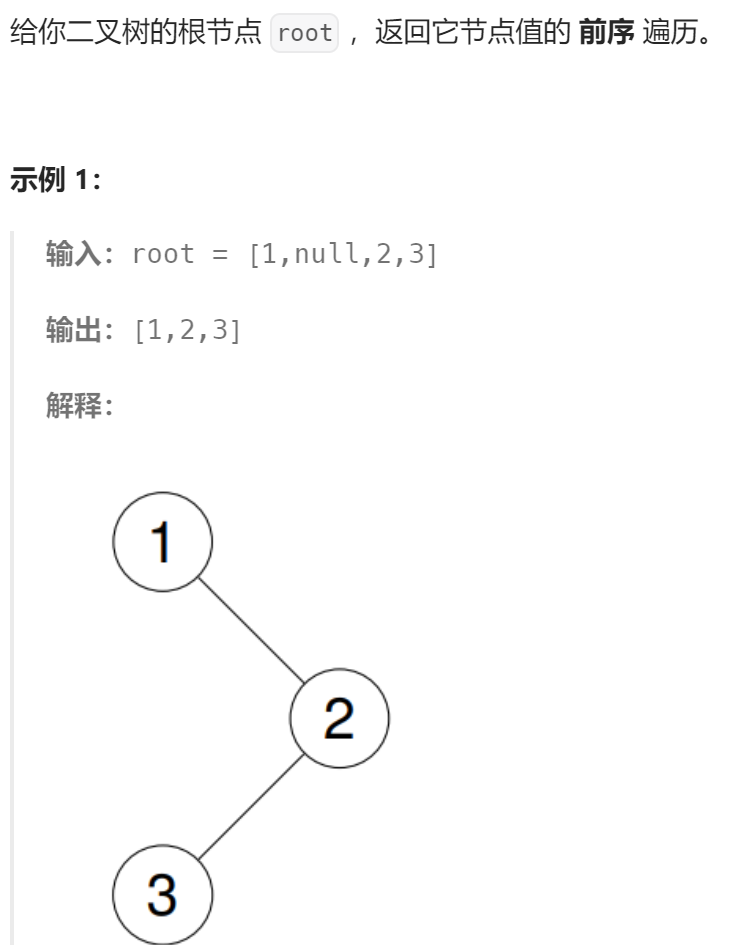
代码实现：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/typedef struct TreeNode TreeNode;
int Treesize(TreeNode*root)
{if(root==NULL){return 0;}return 1+Treesize(root->left)+Treesize(root->right);
}
void preorder(TreeNode*root,int*arr,int*pi)
{if(root==NULL){return;}arr[(*pi)++]=root->val;preorder(root->left,arr,pi);preorder(root->right,arr,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {//要申请几个空间*returnSize=Treesize(root);int*arr=(int*)malloc(sizeof(int)*(*returnSize));int i=0;preorder(root,arr,&i);return arr;}

核心逻辑：

  1. TreeNode 结构体
    定义了二叉树节点的结构，包含节点值 val 和左右子节点指针 left、right。

  2. Treesize 函数

    • 功能：计算二叉树的节点总数（递归实现）。
    • 逻辑：空节点返回 0；非空节点返回「1（当前节点）+ 左子树节点数 + 右子树节点数」。
    • 作用：确定前序遍历结果数组需要申请的内存大小。

  3. preorder 函数

    • 功能：递归执行前序遍历，将节点值存入数组。
    • 参数：
      • root：当前遍历的节点
      • arr：存储结果的数组
      • pi：指向数组索引的指针（用于在递归中共享当前填充位置）
    • 逻辑：先存储当前节点值，再递归遍历左子树，最后递归遍历右子树。

  4. preorderTraversal 函数（主函数）

    • 步骤：
      1. 调用 Treesize 计算节点总数，通过 returnSize 传出（供调用者获取数组长度）。
      2. 根据节点总数用 malloc 动态申请数组内存。
      3. 初始化索引 i=0，调用 preorder 填充数组。
      4. 返回填充好的数组。

注意：

  • 内存管理：数组通过 malloc 申请，调用者需在使用后用 free 释放，避免内存泄漏。
  • 递归限制：对于深度极大的二叉树（如链式结构），递归可能导致栈溢出，此时需改用迭代方式实现。
  • 参数要求：returnSize 必须是有效的 int 指针（不能为 NULL），否则会导致解引用错误。

二叉树遍历（牛客）：

https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef

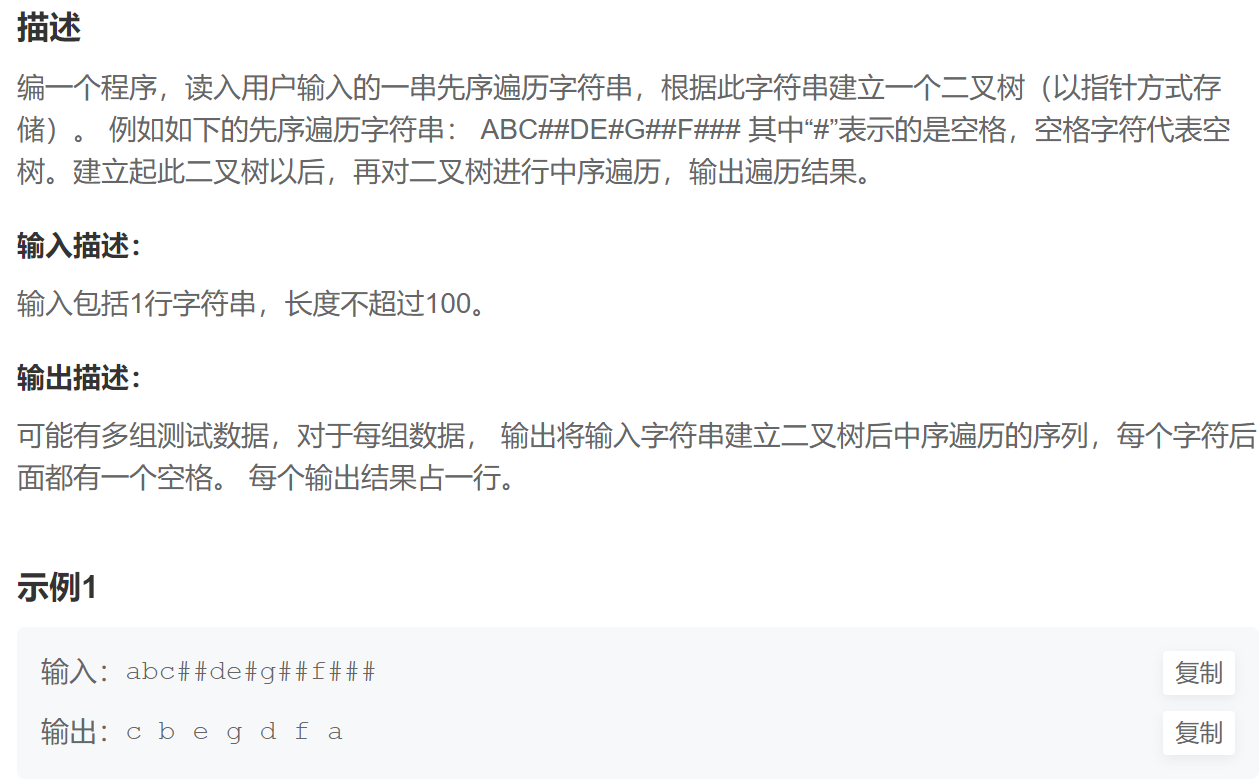
代码实现：  

//二叉树链式结构
#include<stdio.h>
typedef struct TreeNode{int data;struct TreeNode*left;struct TreeNode*right;
}TreeNode;TreeNode*BuyNode(char ch)
{TreeNode*node=(TreeNode*)malloc(sizeof(TreeNode));if(node==NULL){exit(1);}node->data=ch;node->left=node->right=NULL;return node;}
//创建二叉树
TreeNode*createTree(char*arr,int *pi)
{if(arr[*pi]=='#'){(*pi)++;return NULL;}TreeNode*root=BuyNode(arr[*pi]);(*pi)++;root->left=createTree(arr, pi);root->right=createTree(arr, pi);return root;}
void inorder(TreeNode*root)
{if(root==NULL){return ;}inorder(root->left);printf("%c ",root->data);inorder(root->right);
}
int main()
{//读取输入的前序遍历字符串char arr[100];scanf("%s",arr);//根据字符串建立二叉树int i=0;TreeNode*root=createTree(arr, &i);//二叉树的中序遍历inorder(root);
}

加上销毁

// 销毁二叉树（释放所有节点内存）
void DestroyTree(TreeNode* root) {if (root == NULL) {return;}DestroyTree(root->left);   // 先销毁左子树DestroyTree(root->right);  // 再销毁右子树free(root);                // 最后释放当前节点
}

基本逻辑：

  1. TreeNode 结构体：定义二叉树节点，包含数据域 data 和左右子节点指针。
  2. BuyNode 函数：创建新节点，为节点分配内存并初始化。
  3. createTree 函数：根据前序遍历字符串（含 # 表示空节点）递归构建二叉树。
  4. inorder 函数：递归实现二叉树的中序遍历（左 → 根 → 右）并打印节点值。
  5. main 函数：读取输入的前序字符串，构建二叉树并执行中序遍历
http://www.dtcms.com/a/334969.html

相关文章：

  • Dify 从入门到精通（第 38/100 篇）：Dify 的实时协作功能
  • Python---异常链（Exception Chaining）
  • PowerShell 第11章：过滤和比较（上）
  • 深入分析MVCC机制
  • 16.CNN——猫狗二分类识别
  • Git使用和理解上的一些问题
  • ADHD时间感知组件
  • Java 9 新特性及具体应用
  • Flowith-节点式GPT-4 驱动的AI生产力工具
  • PS插件整合包！内置数百款PS插件，支持PS2017-PS2025所有版本！
  • 后量子密码算法SLH-DSA介绍及开源代码实现
  • 【学习嵌入式day-26-线程间通信】
  • Python脚本开发-统计Rte中未连接的Port
  • 鸿蒙应用开发和Vue网页开发中生命周期的区别
  • vue3动态的控制表格列的展示简单例子
  • Python延申内容（一）
  • GDB实战教学
  • LakeHouse--湖仓一体架构
  • 基于C++的词法分析器：使用正则表达式的实现
  • 【OpenGL】LearnOpenGL学习笔记10 - 平行光、点光源、聚光灯
  • Spring Cloud系列—Alibaba Seata分布式事务
  • Linux 文件删除后,df -h磁盘空间未更新
  • 安卓四大组件基础题
  • GPIO初始化及调用
  • Go语言指针与内存分配深度解析：从指针本质到 new、make 的底层实现
  • Spring三级缓存
  • 深入理解 Linux 线程：从概念到虚拟地址空间的全面解析
  • 机器学习的特征工程（特征构造、特征选择、特征转换和特征提取）详解
  • 028 动静态库 —— 动态库
  • 第3问 什么是数据指标？