Java实现汉诺塔问题
什么是汉诺塔问题
有三根柱子 A B C,其中A柱上有n个大小不同的圆盘,按照大的在下,小的在上的顺序,将n个圆盘从A柱移动到C柱上,每次只能移动一个圆盘,移动过程中可以借助B柱作为中转。
【A表示起始柱子,B表示中转柱子,C表示目标柱子】
递归分析
如果只有1个盘子:A->C(直接将这个盘子从起始柱子A移到目标柱子C)
如果有2个盘子:A->B,A->C,B->C(先将小盘子从A移动到B,然后将大盘子从A移到C,最后将小盘子从B移到C,这样所有盘子就按指定的顺序在C柱子上)
如果有3个盘子:A->C,A->B,C->B,A->C,B->A,B->C,A->C(先将小盘子从A移到C,将中盘子从A移到B,然后将小盘子从C移到B,此时小、中盘就都在B柱子上,然后再将大盘子从A移到C,接着再将小盘子从B移到A,将中盘子从B移到C,最后将小盘子从A移到C,这样就将3个盘子按指定的顺序放到了目标柱子C)
我们要用递归来解决这个问题:
首先创建变量 start表示起始柱子'A' helper表示中转柱子'B' end表示目标柱子'C' n表示盘子数量
通过上述的分析,我们知道除了最下层的大盘子外,其余的盘子都是经过中转柱子B再移到目标柱子C的,即我们需要将n-1个盘子先移到B上后,将大盘子移到C上,此时的大盘子C已经成功移到了目标柱子C上,就剩下除了大盘子外的盘子(小、中盘子们),那么此时的最下面的盘子就变成了新的大盘子,它们所在的B柱子就变成了新的起始柱子,将n-1个盘子先通过新的中转柱子A移到C上,最后将大盘子移到C上;重复这个操作,每次将除了大盘子(会变化,每次将一个大盘子移到C上后,在最下面的盘子就变成新的大盘子)外的n-1个盘子先移到中转柱子(会变化)上后,将大盘子移到C上,直到所有的盘子都按指定的顺序(大的在下,小的在上)在目标盘子C上。
注意:在每次移动的过程中,起始柱子和中转柱子是会随着变化的
代码说明
核心方法:
hanio(n , start , end , heiper):递归求解汉诺塔问题
参数说明:
- n:要移动的盘子数量
- start:起始柱子,字符'A'
- end:目标柱子,字符'C'
- helper:中转柱子,字符'B'
递归逻辑:
- 当只有一个盘子时(递归基),直接移动
- 当有多个盘子时:
- 先将上面n-1个盘子移到中转柱
- 移动最底层的盘子到目标柱
- 最后将n-1个盘子从中转柱移到目标柱
完整代码
public class Hanio{public static void main(String[] args){int n = 3;//3个盘子hanio(n,'A','C','B');}public static void hanio(int n,char start,char end,char helper){//只有1个盘子if(n == 1){System.out.println("移动盘子1从" + start + "->" + end);return;}//1.将上面n-1个盘子移到中转柱Bhanio(n-1,start,helper,end);//2.移动最底层的盘子到目标柱子C System.out.println("移动盘子" + n + "从" + start + "->" + end);//3.将n-1个盘子从中转柱B移到目标柱Chanio(n-1,helper,end,start);}
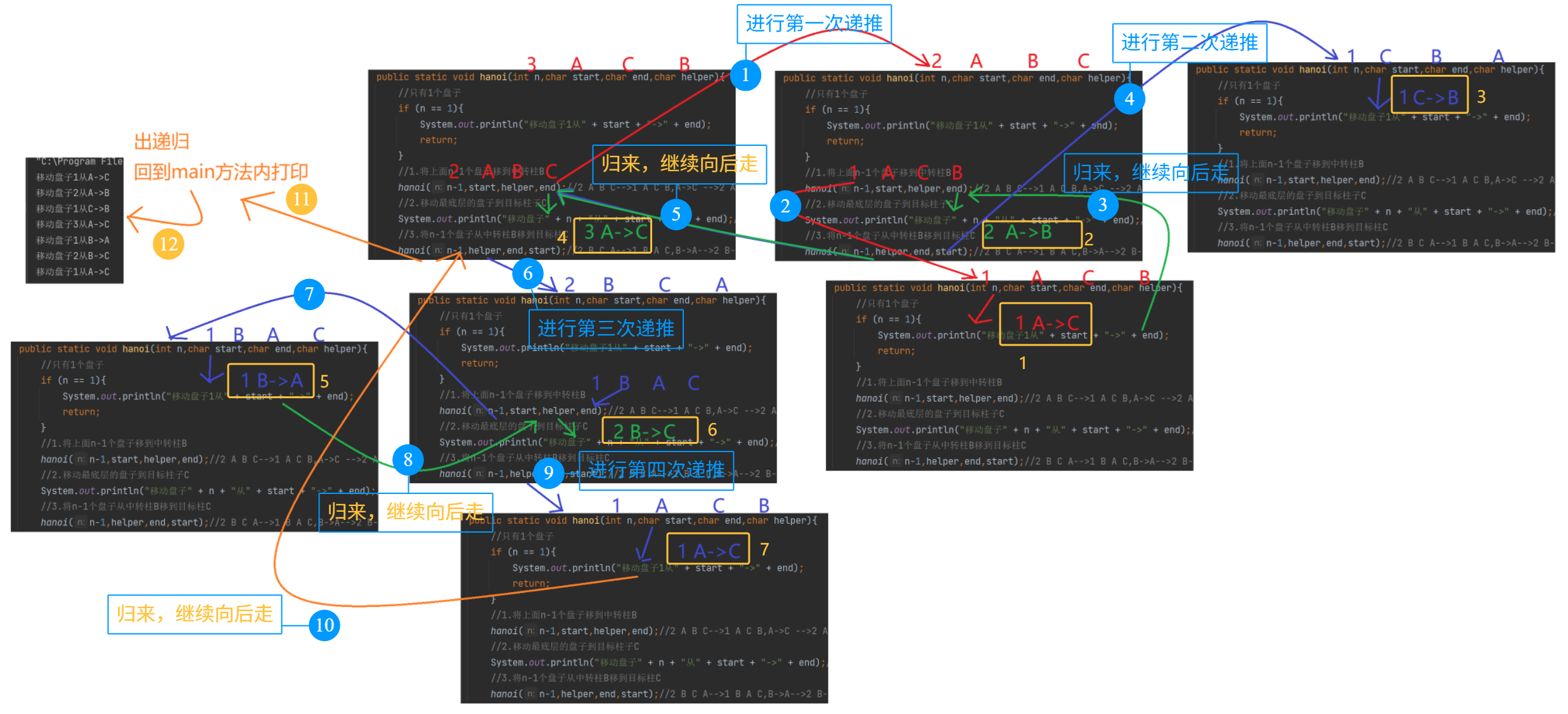
}图解递归过程(n=3为例):
初始状态:
A: [3,2,1] B: [ ] C: [ ]1. 移动上面2个盘子到B柱(递归调用):
- 移动1号盘 A→C
- 移动2号盘 A→B
- 移动1号盘 C→B
此时:A: [3] B: [2,1] C: [ ]2. 移动最底层的3号盘:A→C
此时:A: [ ] B: [2,1] C: [3]3. 移动B柱的2个盘子到C柱(递归调用):
- 移动1号盘 B→A
- 移动2号盘 B→C
- 移动1号盘 A→C
此时:A: [ ] B: [ ] C: [3,2,1]
更详细版本(展开递归调用):
hanoi(3, A, C, B)
├── hanoi(2, A, B, C)
│ ├── hanoi(1, A, C, B) → 移动1: A→C
│ ├── 移动2: A→B
│ └── hanoi(1, C, B, A) → 移动1: C→B
├── 移动3: A→C
└── hanoi(2, B, C, A)
├── hanoi(1, B, A, C) → 移动1: B→A
├── 移动2: B→C
└── hanoi(1, A, C, B) → 移动1: A→C
如果这里还是不太懂到底如何递归,请往下看代码版的递归图解:
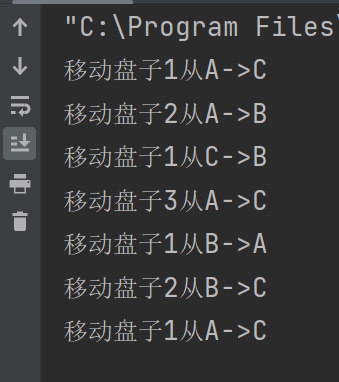
看这个运行结果和我们上面分析的3个盘子的走向一致
(盘子1,2,3指的就是小、中、大盘子的意思)
