从模拟实现插入去理解AVL树的旋转平衡

AVL树是一种遵循严格左右对称的搜索二叉树，它左右子树的高度差不超过1，这样就可以避免搜索二叉树可能出现的单边子树过长带来的时间复杂度不理想的问题，达到搜索树原本理想的n(logn)。为了左右子树的平衡，它引入了平衡因子这个概念，每个结点都有⼀个平衡因⼦，任一结点的平衡因⼦等于右子树的高度减去左子树的高度，也就是说任何结点的平衡因⼦等于0/1/-1，AVL树并不是必须要平衡因⼦，但是有了平衡因⼦可以更⽅便我们去进⾏观察和控制树是否平衡。

接下来实现一下它的整体结构：

//.h
template<class K, class V>
struct AVLTreeNode
{
// 需要parent指针，后续更新平衡因⼦可以看到pair<K, V> _kv;//用来存储键值对数据，与整体结构没太大关系，不用太关注AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // 平衡因子AVLTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr),_bf(0){}
};
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){//...}
private:Node* _root = nullptr;
};

接下来就开始实现着重关注的插入函数：

思路：1.完成插入步骤，数据的插入和搜索二叉树的插入一样，小了往左走，大了往右，找到末尾后再让新节点cur与parent比较决定插在左边还是右边。

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;} Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;} else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;} else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//...
}

2.更新平衡因子。因为平衡因子=右子树的高度-左子树的高度，所以插在左边，parent的平衡因子就--，在右边就++。当然，插入也有可能会影响到parent往上的那些节点，也要更新。为什么是有可能呢？因为如果parent的一边正好是空的，cur插入的是那个刚好的空位，那么上面那些节点的左右子树高度就没变化，不用往上更新了，总结一下就是当cur和parent的平衡因子更新完为0就结束更新，否则继续往上更新上面节点的平衡因子。

3.处理不平衡情况。插入可能会导致平衡因子超出-1到1的范围，这意味着左右子树高度差变为2，需要旋转来调整。现在先展示代码，接下来详细解释。

	//第一步的代码// 2.更新平衡因⼦while (parent){// 更新平衡因⼦if (cur == parent->_left)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0){// 更新结束break;}else if (parent->_bf == 1 || parent->_bf == -1){// 继续往上更新cur = parent;parent = parent->_parent;}// 3.不平衡了，旋转处理else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);//右单旋}else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);//左单旋}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);//左右双旋}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);//右左双旋}else{assert(false);}break;}//预防不是-1,0,1和2，-2的未知情况else{assert(false);}}

插入后导致高度差为2或-2的有4种情况，由于大树是由一个个小树组成，接下来的示例图抽象成一个模型来解释具体到图形是怎样的，对应四种旋转方式：

第一种：右单旋

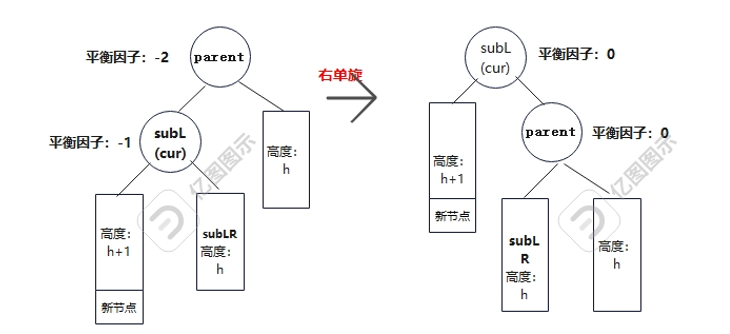
对应的是parent的左子树比较高，cur也是左子树较高的情况，用平衡因子来表现就是parent平衡因子为-2，cur为parent的左子树且平衡因子为-1。插入位置在cur的左子树。

右单旋就是让cur的右子树（subLR）向右旋转作为parent的的左子树，再让修改后的parent作为cur的右子树，这里为了方便理解位置，subL就是cur，subLR就是cur的右子树，具体如下图：

（没绘图软件的VIP，导出不给去水印 T-T）

整体思路就是这样，直接看代码（这里比较容易忘记修改cur的_parent，记得在parent的_parent被修改之前记录一下）

void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;// 需要注意除了要修改孩⼦指针指向，还是修改⽗亲parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;// parent有可能是整棵树的根，也可能是局部的⼦树// 如果是整棵树的根，要修改_root// 如果是局部的指针要跟上⼀层链接if (parentParent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}parent->_bf = subL->_bf = 0;
}

第二种：左单旋

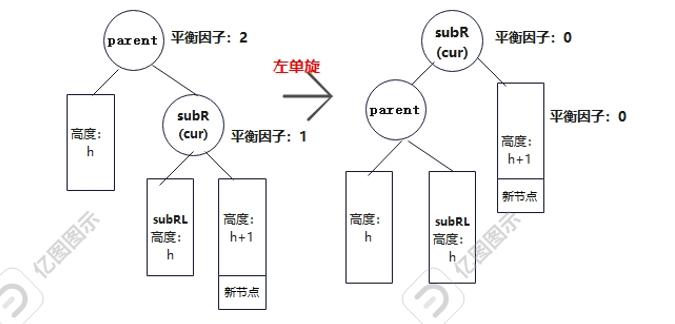
对应的是parent的右子树比较高，cur也是右子树较高的情况，用平衡因子来表现就是parent平衡因子为2，cur为parent的右子树且平衡因子为1。插入位置在cur的右子树。整体思路和右单旋类似，让cur的左子树向左旋转作为parent的的右子树，再让修改后的parent作为cur的左子树。图，代码如下：

void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* parentParent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parentParent == nullptr){_root = subR;subR->_parent = nullptr;} else{if (parent == parentParent->_left){parentParent->_left = subR;} else{parentParent->_right = subR;} subR->_parent = parentParent;} parent->_bf = subR->_bf = 0;
}

第三种：左右双旋

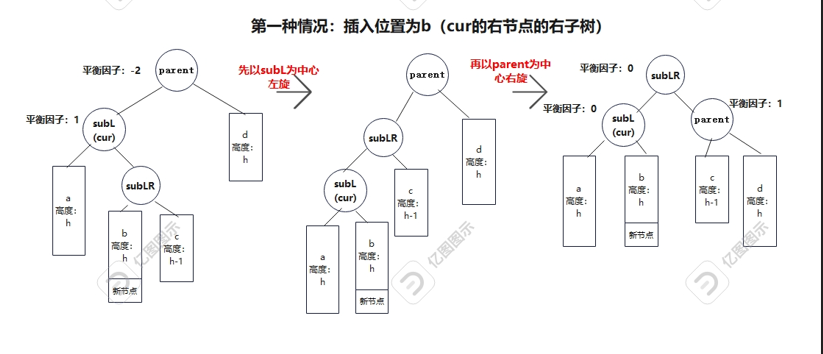
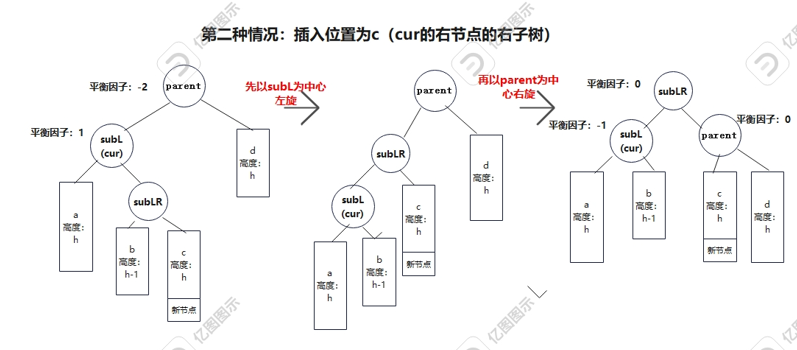
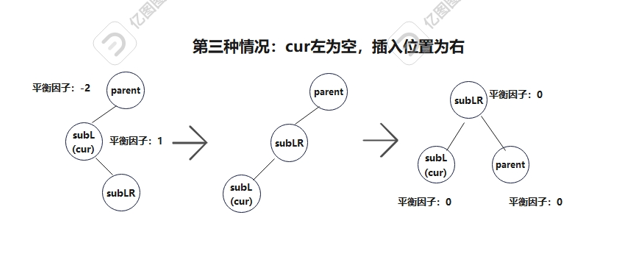
对应的是parent的左子树比较高，cur右子树较高的情况，用平衡因子来表答就是parent平衡因子为-2，cur为parent的左子树且平衡因子为1。由于这种情况需要经过两次旋转，所以要细分一下，插入位置有三种可能，在cur的右节点的左子树或右子树还有cur左为空，插入位置为右的情况。

下面用图演示是怎么旋转的：

（其实从整体来理解就是把b给subL，c给parent，然后subLR做根，subL和parent分别作为它的左右子树）

对应代码：

void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);//更新平衡因子if (bf == 0)//第三种情况{subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;} else if (bf == -1)//第一种情况{subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;} else if (bf == 1)//第二种情况{subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;} else{assert(false);}
}

第四种：右左双旋

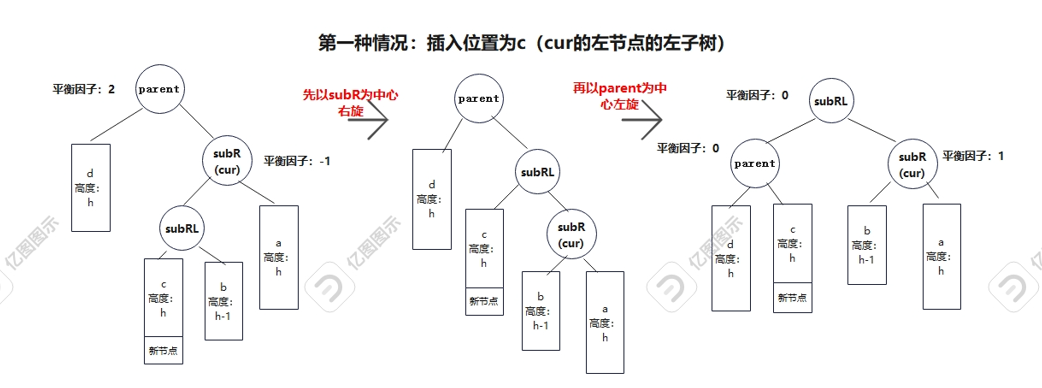
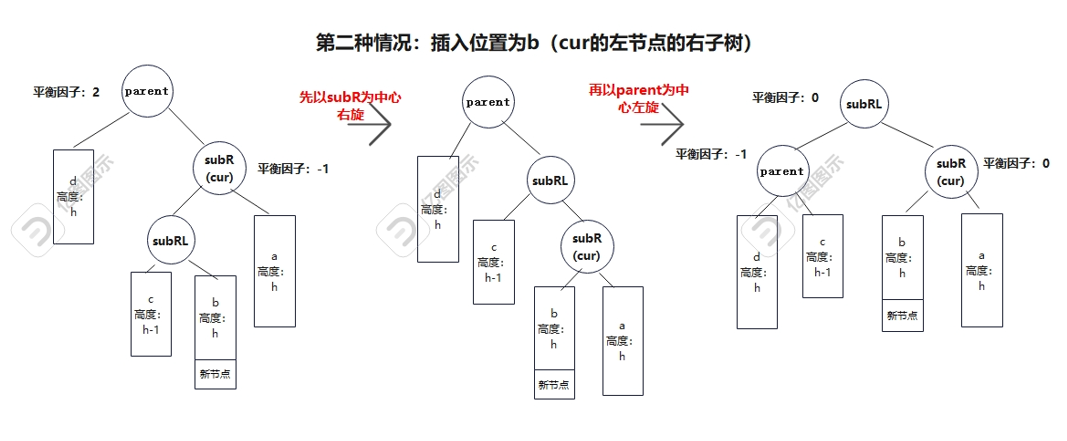
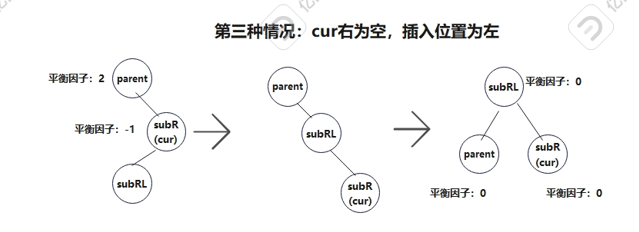
对应的是parent的右子树比较高，cur左子树较高的情况，用平衡因子来表达就是parent平衡因子为2，cur为parent的左子树且平衡因子为-1。同样需要经过两次旋转，先右旋再左旋，插入位置有三种可能，在cur的左节点的左子树或右子树还有cur右为空，插入位置为左的情况。

思路和左右双旋类似：

（从整体来理解就是把b给subR，c给parent，然后subRL做根，parent和subR分别作为它的左右子树）

代码如下：

void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);//更新平衡因子if (bf == 0)//第三种情况{subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;} else if (bf == 1)//第一种情况{subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;} else if (bf == -1)//第二种情况{subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;} else{assert(false);}
}