当前位置：首页 > news >正文

《算法导论》第 25 章：所有结点对的最短路径问题

news 2025/8/15 9:03:53

引言

在图论中，所有结点对的最短路径问题是一个经典且重要的问题，它要求我们找出图中每对顶点之间的最短路径。这个问题在交通导航、网络路由、社交网络分析等领域都有广泛应用。

本章将详细介绍三种解决所有结点对最短路径问题的经典算法：

基于矩阵乘法的最短路径算法
Floyd-Warshall 算法
适用于稀疏图的 Johnson 算法

下面让我们逐一学习这些算法的原理、实现和应用。

思维导图

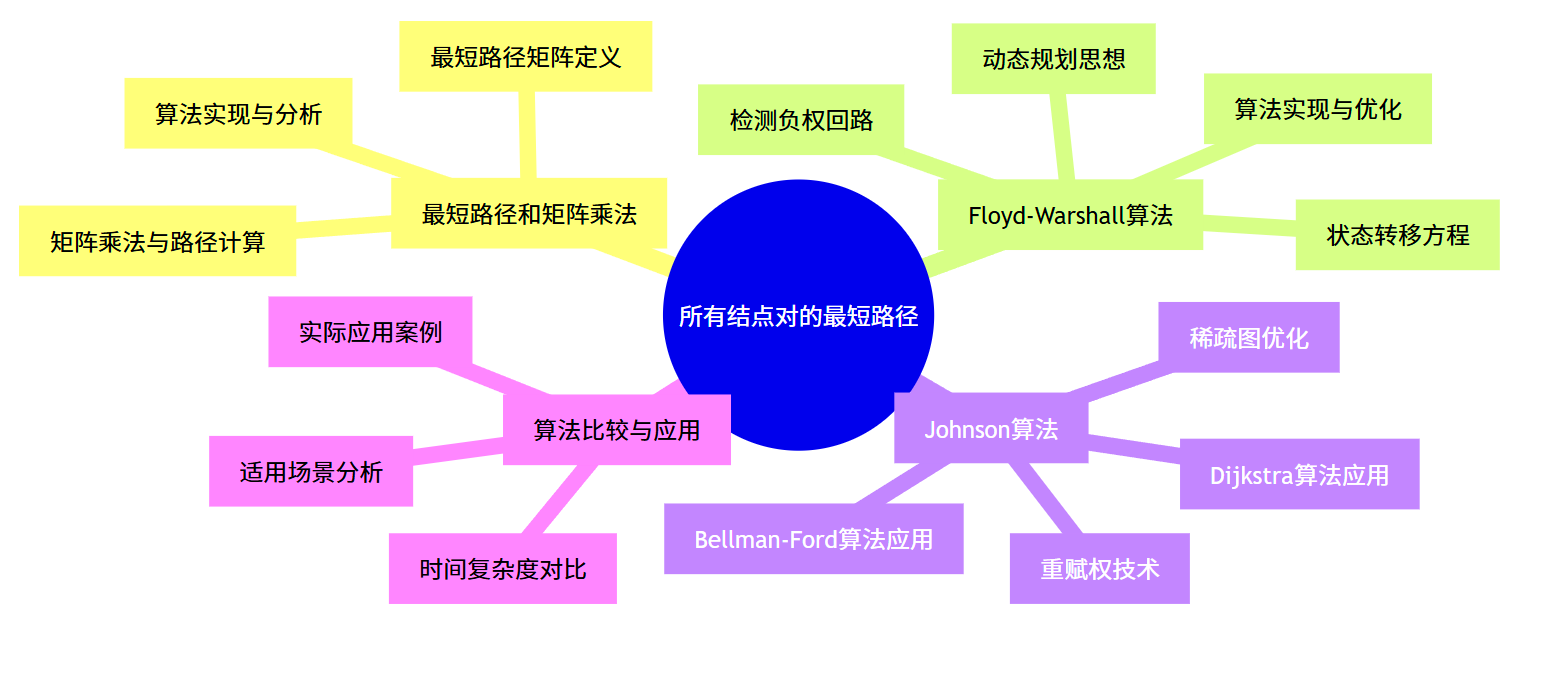
25.1 最短路径和矩阵乘法

基本思想

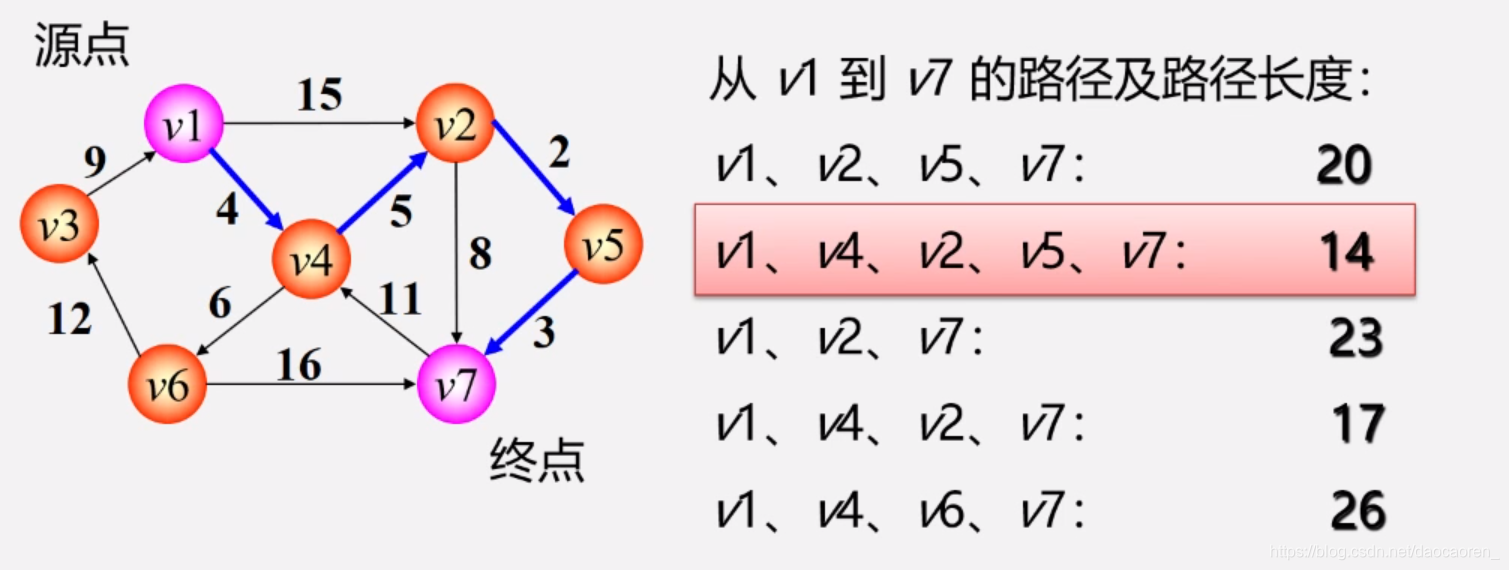
最短路径问题可以与矩阵乘法建立联系。我们可以定义一种 "矩阵乘法" 操作，用于合并路径。通过这种操作，我们可以计算出图中所有结点对之间的最短路径。

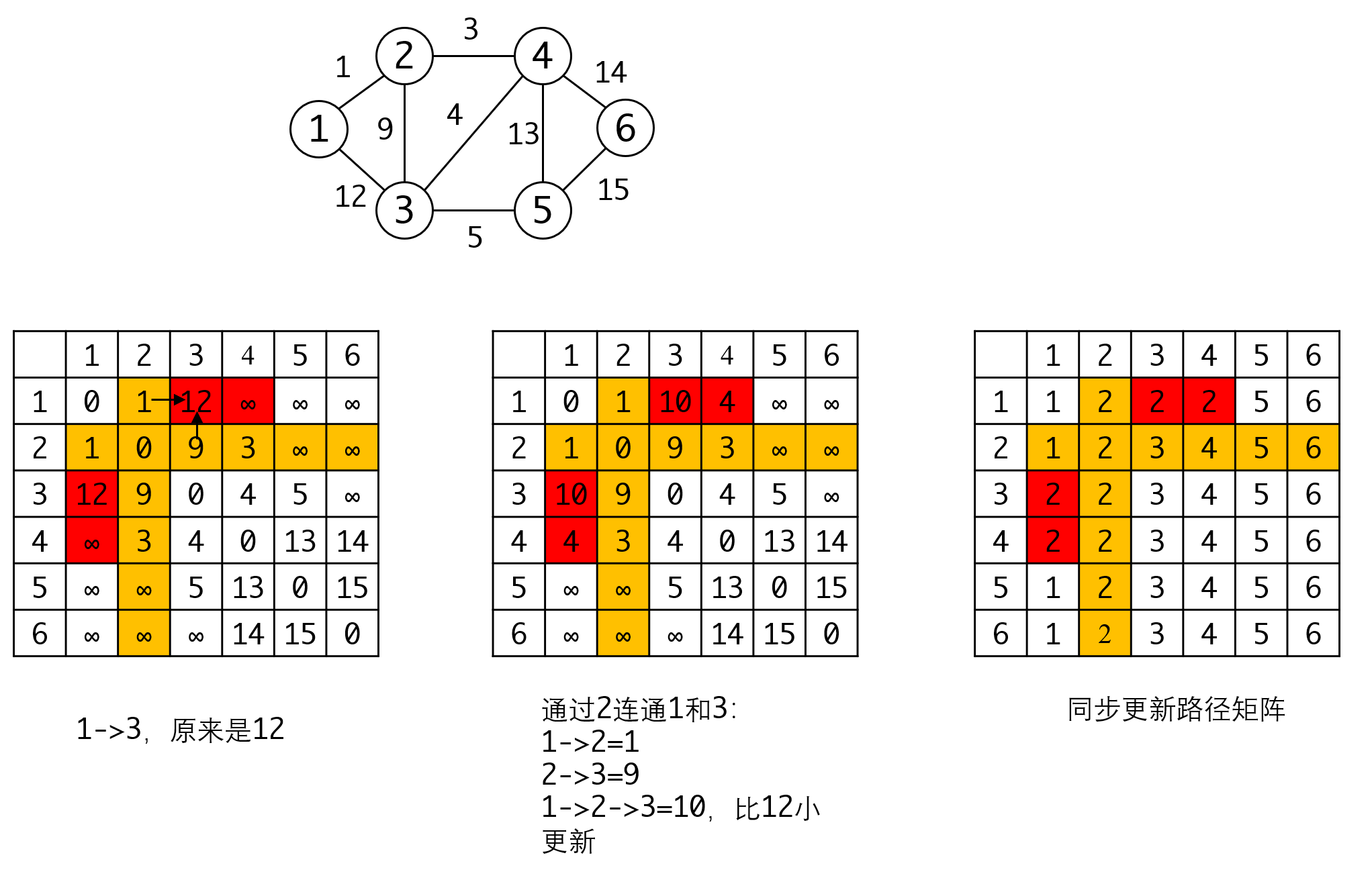
具体来说，我们定义一个 n×n 的矩阵L，其中L[i][j]表示从结点 i 到结点 j 的最短路径权重。我们的目标是计算出这个矩阵 L。

路径合并操作

我们定义一种类似于矩阵乘法的操作⊙：对于两个 n×n 的矩阵 A 和 B，它们的 "乘积"C = A ⊙ B 定义为：

C [i][j] = min { A [i][k] + B [k][j] } 对于所有 k = 1, 2, ..., n

这个操作的意义是：从 i 到 j 的路径，中间经过 k 的最短路径权重。

算法流程

初始化矩阵L(1)，其中L(1)[i][j]是直接从 i 到 j 的边的权重（如果没有直接边，则为无穷大）
对于 m = 2 到 n-1，计算L(m) = L(m-1) ⊙ L(1)
最终结果L(n-1)就是所有结点对之间的最短路径矩阵

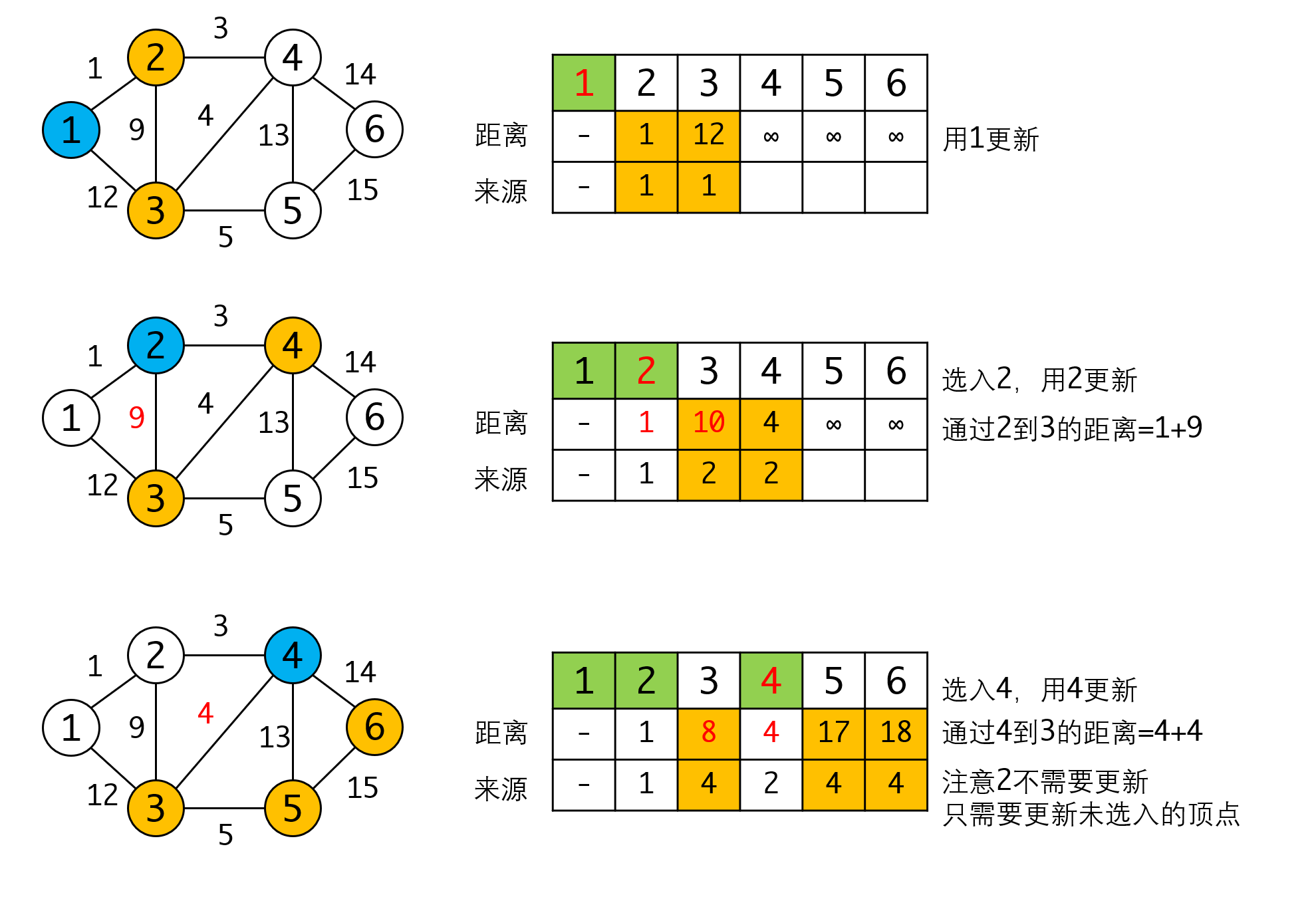
因为任意两个结点之间的最短路径最多包含 n-1 条边，所以经过 n-1 次合并操作后，我们就能得到所有结点对之间的最短路径。

代码实现

下面是基于矩阵乘法的最短路径算法的 C++ 实现：

#include <iostream>
#include <vector>
#include <climits>
using namespace std;// 定义无穷大
const int INF = INT_MAX / 2;  // 使用INT_MAX/2避免加法溢出// 打印矩阵
void printMatrix(const vector<vector<int>>& mat) {int n = mat.size();for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (mat[i][j] == INF) {cout << "INF\t";} else {cout << mat[i][j] << "\t";}}cout << endl;}
}// 矩阵合并操作 A ⊙ B
vector<vector<int>> matrixMultiply(const vector<vector<int>>& A, const vector<vector<int>>& B) {int n = A.size();vector<vector<int>> result(n, vector<int>(n, INF));for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {for (int k = 0; k < n; ++k) {// 计算A[i][k] + B[k][j]，并与当前结果比较取最小值result[i][j] = min(result[i][j], A[i][k] + B[k][j]);}}}return result;
}// 基于矩阵乘法的所有结点对最短路径算法
vector<vector<int>> allPairsShortestPaths(const vector<vector<int>>& graph) {int n = graph.size();vector<vector<int>> L = graph;  // L(1)初始化为图的邻接矩阵// 迭代计算L(2), L(3), ..., L(n-1)for (int m = 2; m < n; ++m) {L = matrixMultiply(L, graph);}return L;
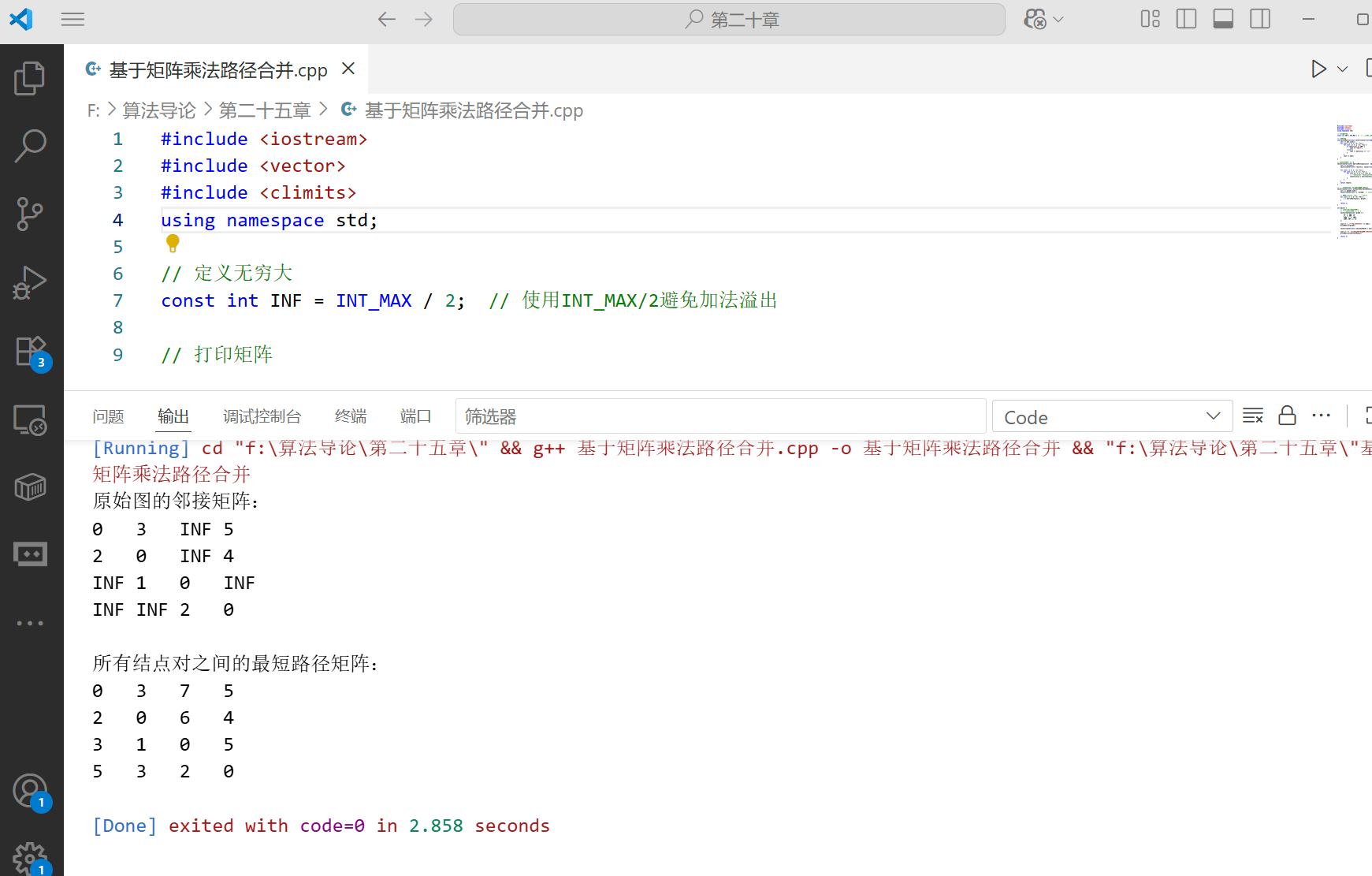
}int main() {// 示例图的邻接矩阵表示// 图中有4个结点0, 1, 2, 3vector<vector<int>> graph = {{0, 3, INF, 5},{2, 0, INF, 4},{INF, 1, 0, INF},{INF, INF, 2, 0}};cout << "原始图的邻接矩阵：" << endl;printMatrix(graph);vector<vector<int>> shortestPaths = allPairsShortestPaths(graph);cout << "\n所有结点对之间的最短路径矩阵：" << endl;printMatrix(shortestPaths);return 0;
}

算法分析

时间复杂度：算法需要进行 n-2 次矩阵合并操作，每次矩阵合并的时间复杂度为 O (n³)，因此总的时间复杂度为 O (n⁴)。这个复杂度相对较高，实际应用中很少直接使用这种方法。
空间复杂度：O (n²)，主要用于存储矩阵。

优化思路

我们可以使用二进制提升的思想来优化这个算法，将时间复杂度降低到 O (n³ log n)：

计算 L (1), L (2), L (4), L (8), ..., 直到 L (2^k)，其中 2^k < n
将这些矩阵合并，得到 L (n-1)

下面是优化版本的代码实现：

#include <iostream>
#include <vector>
#include <climits>
using namespace std;const int INF = INT_MAX / 2;// 打印矩阵
void printMatrix(const vector<vector<int>>& mat) {int n = mat.size();for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (mat[i][j] == INF) {cout << "INF\t";} else {cout << mat[i][j] << "\t";}}cout << endl;}
}// 矩阵合并操作 A ⊙ B
vector<vector<int>> matrixMultiply(const vector<vector<int>>& A, const vector<vector<int>>& B) {int n = A.size();vector<vector<int>> result(n, vector<int>(n, INF));for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {for (int k = 0; k < n; ++k) {result[i][j] = min(result[i][j], A[i][k] + B[k][j]);}}}return result;
}// 基于二进制提升的优化算法
vector<vector<int>> optimizedAllPairsShortestPaths(const vector<vector<int>>& graph) {int n = graph.size();if (n <= 1) return graph;// 初始化结果为单位矩阵（路径长度为0的矩阵）vector<vector<int>> result(n, vector<int>(n, INF));for (int i = 0; i < n; ++i) {result[i][i] = 0;}vector<vector<int>> current = graph;  // 当前要合并的矩阵int m = 1;  // 当前矩阵表示的最大路径长度while (m < n - 1) {// 如果m小于n-1，并且下一次翻倍不会超过n-1，则合并if (2 * m <= n - 1) {current = matrixMultiply(current, current);m *= 2;} else {// 否则，合并当前结果与current，然后退出循环result = matrixMultiply(result, current);m = n - 1;  // 标记为完成}}// 最后合并结果与currentresult = matrixMultiply(result, current);return result;
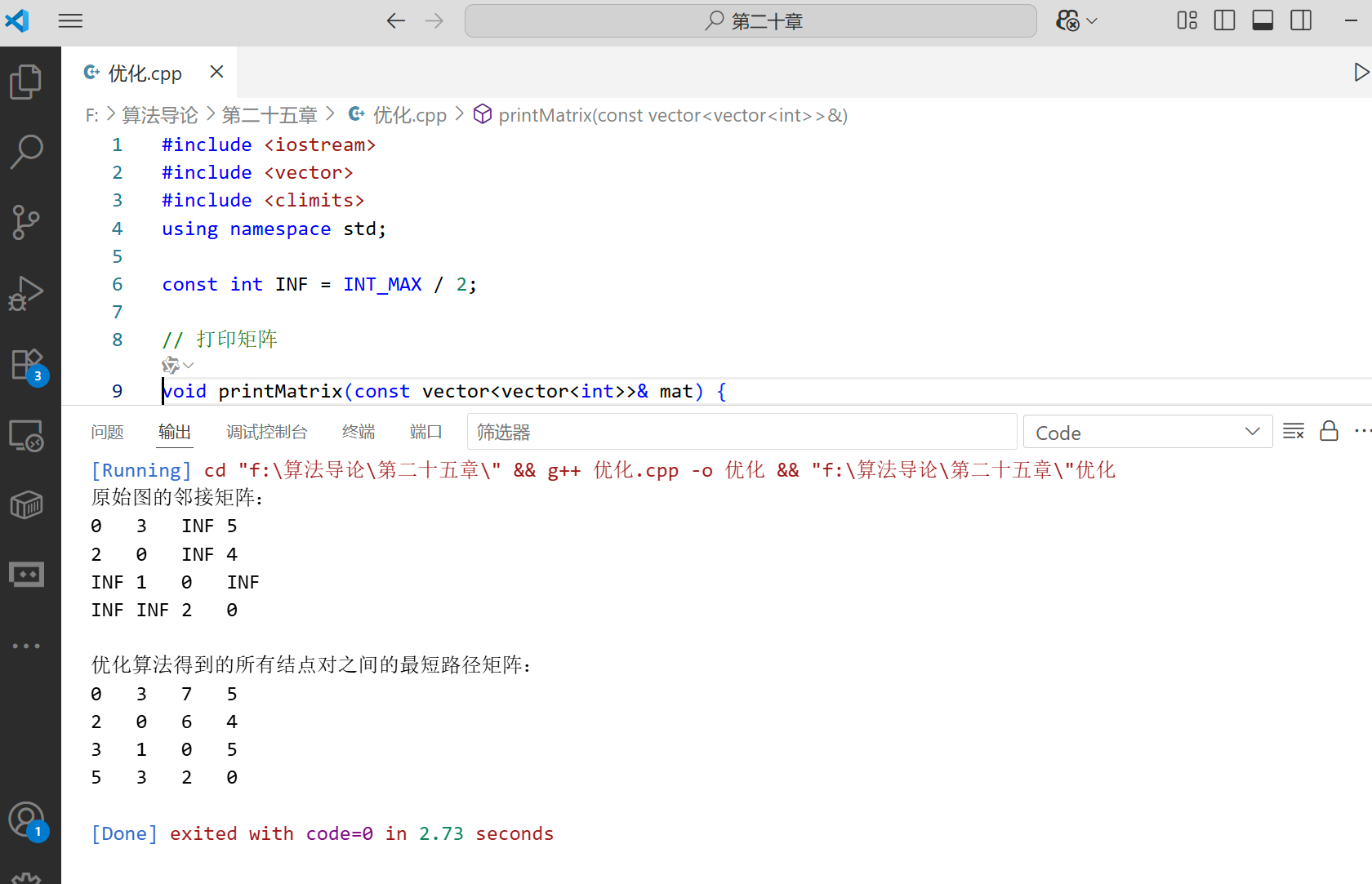
}int main() {vector<vector<int>> graph = {{0, 3, INF, 5},{2, 0, INF, 4},{INF, 1, 0, INF},{INF, INF, 2, 0}};cout << "原始图的邻接矩阵：" << endl;printMatrix(graph);vector<vector<int>> shortestPaths = optimizedAllPairsShortestPaths(graph);cout << "\n优化算法得到的所有结点对之间的最短路径矩阵：" << endl;printMatrix(shortestPaths);return 0;
}

25.2 Floyd-Warshall 算法

基本思想

Floyd-Warshall 算法是一种动态规划算法，用于求解所有结点对之间的最短路径问题。它的基本思想是：

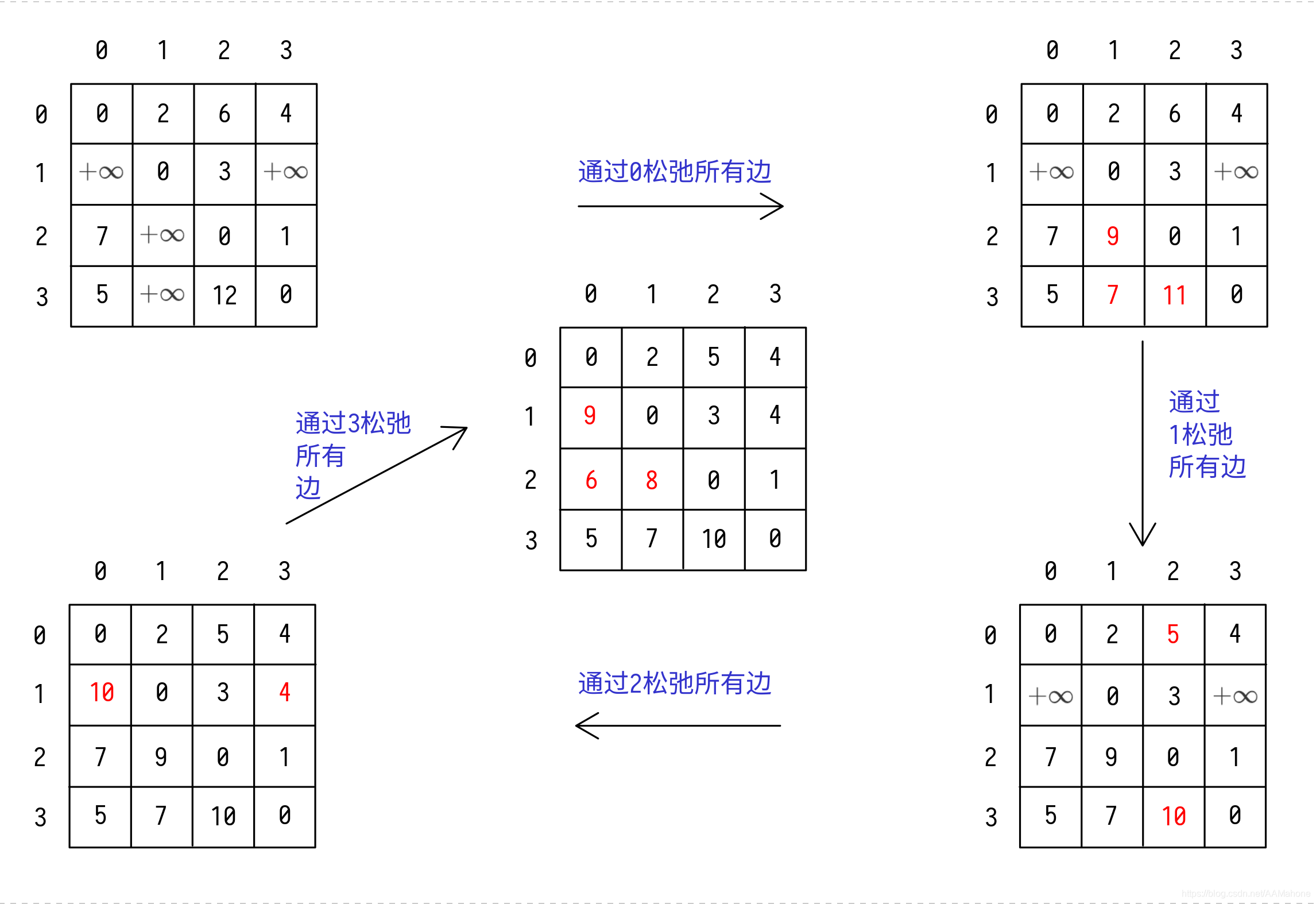
对于任意两个结点 i 和 j，它们之间的最短路径要么直接从 i 到 j，要么经过某个中间结点 k。因此，我们可以通过考虑所有可能的中间结点来逐步改进最短路径的估计值。

动态规划状态定义

定义d[k][i][j]为从 i 到 j，且中间结点只能是 {0, 1, ..., k} 集合中的结点时的最短路径权重。

根据这个定义，我们可以得到状态转移方程：

d[k][i][j] = min(d[k-1][i][j], d[k-1][i][k] + d[k-1][k][j])

当 k = -1 时，d[-1][i][j]就是直接从 i 到 j 的边的权重（如果没有直接边，则为无穷大）
最终结果是d[n-1][i][j]，即允许所有结点作为中间结点时的最短路径

空间优化

注意到计算d[k]时只需要用到d[k-1]的值，因此我们可以使用一个二维数组来存储中间结果，将空间复杂度从 O (n³) 优化到 O (n²)。

优化后的状态转移方程为：

d[i][j] = min(d[i][j], d[i][k] + d[k][j])

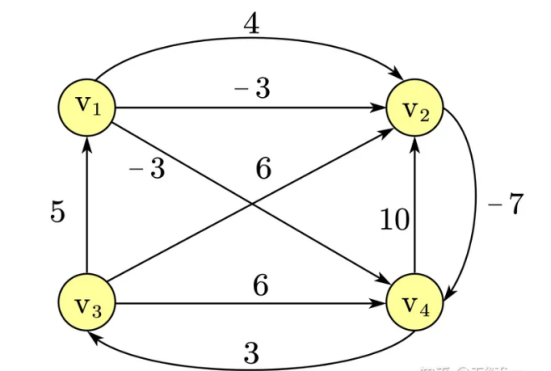
代码实现

下面是 Floyd-Warshall 算法的 C++ 实现：

#include <iostream>
#include <vector>
#include <climits>
using namespace std;const int INF = INT_MAX / 2;  // 避免加法溢出// 打印矩阵
void printMatrix(const vector<vector<int>>& mat) {int n = mat.size();for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (mat[i][j] == INF) {cout << "INF\t";} else {cout << mat[i][j] << "\t";}}cout << endl;}
}// Floyd-Warshall算法实现
void floydWarshall(vector<vector<int>>& dist) {int n = dist.size();// 依次考虑以每个结点k为中间结点for (int k = 0; k < n; ++k) {// 遍历所有可能的起点ifor (int i = 0; i < n; ++i) {// 遍历所有可能的终点jfor (int j = 0; j < n; ++j) {// 更新i到j的最短路径dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);}}}
}// 扩展：不仅计算最短路径长度，还记录路径
void floydWarshallWithPath(vector<vector<int>>& dist, vector<vector<int>>& path) {int n = dist.size();// 初始化路径矩阵for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i == j) {path[i][j] = -1;  // 自身到自身没有路径} else if (dist[i][j] != INF) {path[i][j] = i;   // 直接路径，前驱是起点} else {path[i][j] = -1;  // 无路径}}}// Floyd-Warshall算法主过程for (int k = 0; k < n; ++k) {for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (dist[i][k] + dist[k][j] < dist[i][j]) {dist[i][j] = dist[i][k] + dist[k][j];path[i][j] = path[k][j];  // 更新路径}}}}
}// 打印从i到j的最短路径
void printPath(const vector<vector<int>>& path, int i, int j) {if (i == j) {cout << i;return;}if (path[i][j] == -1) {cout << "无路径";return;}printPath(path, i, path[i][j]);cout << " -> " << j;
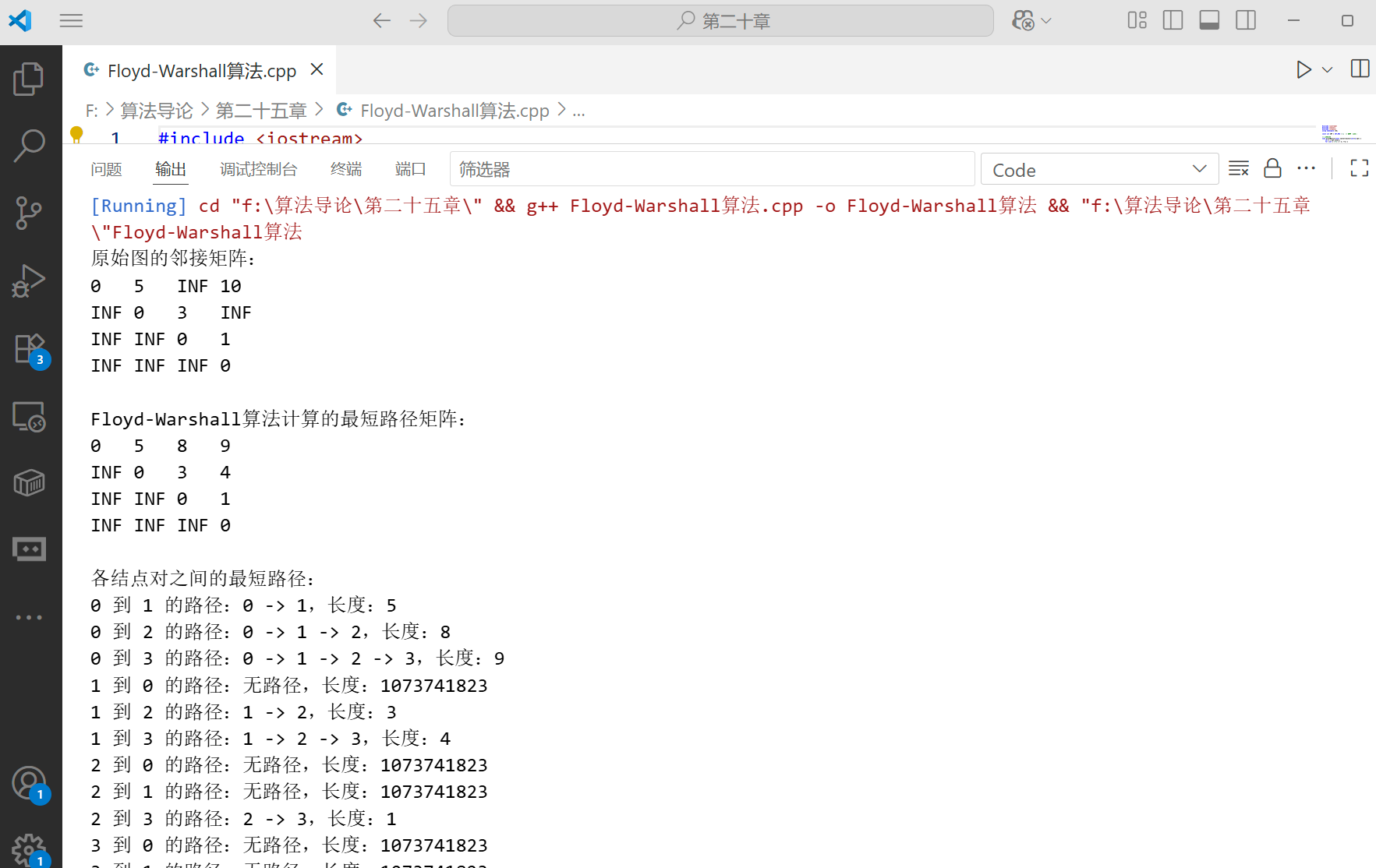
}int main() {// 示例图的邻接矩阵vector<vector<int>> graph = {{0, 5, INF, 10},{INF, 0, 3, INF},{INF, INF, 0, 1},{INF, INF, INF, 0}};int n = graph.size();cout << "原始图的邻接矩阵：" << endl;printMatrix(graph);// 计算最短路径vector<vector<int>> dist = graph;floydWarshall(dist);cout << "\nFloyd-Warshall算法计算的最短路径矩阵：" << endl;printMatrix(dist);// 计算最短路径并记录路径vector<vector<int>> dist2 = graph;vector<vector<int>> path(n, vector<int>(n, -1));floydWarshallWithPath(dist2, path);cout << "\n各结点对之间的最短路径：" << endl;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i != j) {cout << i << " 到 " << j << " 的路径：";printPath(path, i, j);cout << "，长度：" << dist2[i][j] << endl;}}}return 0;
}

算法分析

时间复杂度：O (n³)，其中 n 是图中结点的数量。算法有三重嵌套循环，每层循环都执行 n 次。
空间复杂度：O (n²)，用于存储距离矩阵和路径矩阵（如果需要记录路径）。

检测负权回路

Floyd-Warshall 算法还可以用于检测图中是否存在负权回路。具体方法是：

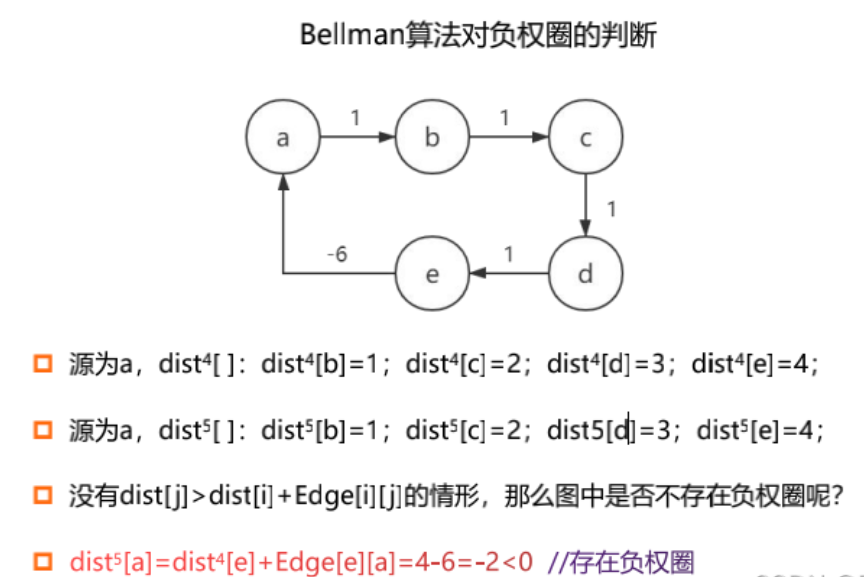
在计算完所有结点对之间的最短路径后，检查是否存在结点 i，使得dist[i][i] < 0。如果存在这样的结点，说明图中存在负权回路，因为从 i 出发经过某个回路回到 i 的总权重为负数。

下面是检测负权回路的代码实现：

// 检测图中是否存在负权回路
bool hasNegativeCycle(const vector<vector<int>>& dist) {int n = dist.size();// 检查是否存在结点i，使得从i到i的最短路径权重为负数for (int i = 0; i < n; ++i) {if (dist[i][i] < 0) {return true;}}return false;
}// 示例：测试负权回路检测
int main() {// 包含负权回路的图vector<vector<int>> graphWithNegativeCycle = {{0, 1, INF},{INF, 0, -1},{-1, INF, 0}};vector<vector<int>> dist = graphWithNegativeCycle;floydWarshall(dist);if (hasNegativeCycle(dist)) {cout << "图中存在负权回路" << endl;} else {cout << "图中不存在负权回路" << endl;}return 0;
}

应用案例：交通网络最短路径

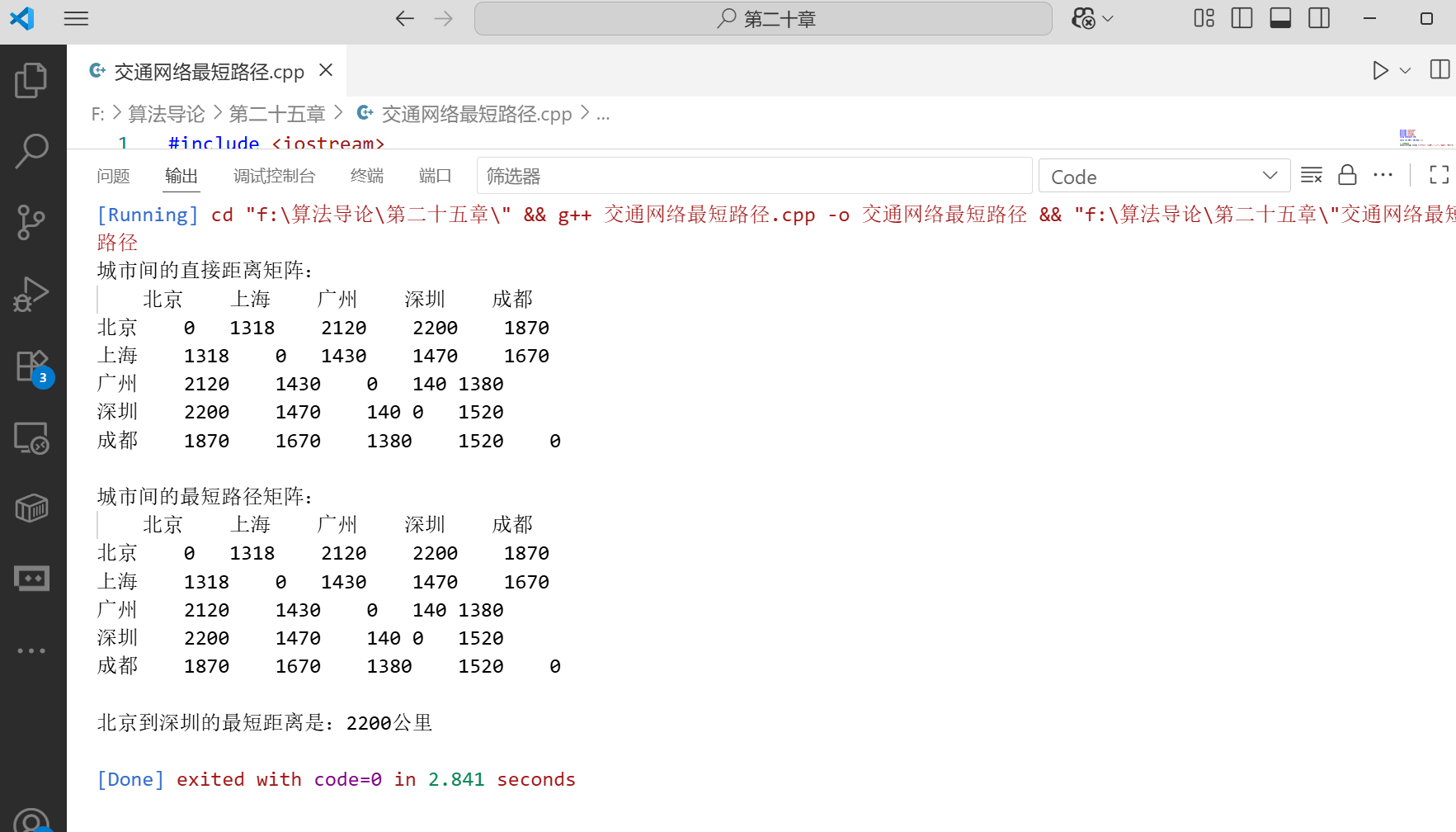
Floyd-Warshall 算法非常适合解决交通网络中的最短路径问题。下面是一个城市间交通网络的例子：

#include <iostream>
#include <vector>
#include <string>
#include <climits>
using namespace std;const int INF = INT_MAX / 2;// 城市名称
vector<string> cities = {"北京", "上海", "广州", "深圳", "成都"};// 打印矩阵（带城市名称）
void printCityMatrix(const vector<vector<int>>& mat) {int n = mat.size();cout << "\t";for (const string& city : cities) {cout << city << "\t";}cout << endl;for (int i = 0; i < n; ++i) {cout << cities[i] << "\t";for (int j = 0; j < n; ++j) {if (mat[i][j] == INF) {cout << "INF\t";} else {cout << mat[i][j] << "\t";}}cout << endl;}
}// Floyd-Warshall算法实现（同上，略）
void floydWarshall(vector<vector<int>>& dist) {// 实现代码同上int n = dist.size();for (int k = 0; k < n; ++k) {for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);}}}
}int main() {// 城市间的距离矩阵（单位：公里）vector<vector<int>> distance = {{0, 1318, 2120, 2200, 1870},    // 北京到其他城市的距离{1318, 0, 1430, 1470, 1670},    // 上海到其他城市的距离{2120, 1430, 0, 140, 1380},     // 广州到其他城市的距离{2200, 1470, 140, 0, 1520},     // 深圳到其他城市的距离{1870, 1670, 1380, 1520, 0}     // 成都到其他城市的距离};cout << "城市间的直接距离矩阵：" << endl;printCityMatrix(distance);// 计算所有城市对之间的最短路径floydWarshall(distance);cout << "\n城市间的最短路径矩阵：" << endl;printCityMatrix(distance);// 示例：查询北京到深圳的最短路径int beijing = 0, shenzhen = 3;cout << "\n" << cities[beijing] << "到" << cities[shenzhen] << "的最短距离是：" << distance[beijing][shenzhen] << "公里" << endl;return 0;
}

25.3 用于稀疏图的 Johnson 算法

基本思想

Johnson 算法是一种结合了 Bellman-Ford 算法和 Dijkstra 算法的算法，专门用于求解稀疏图中所有结点对之间的最短路径问题。它的主要优势是在稀疏图上比 Floyd-Warshall 算法更高效。

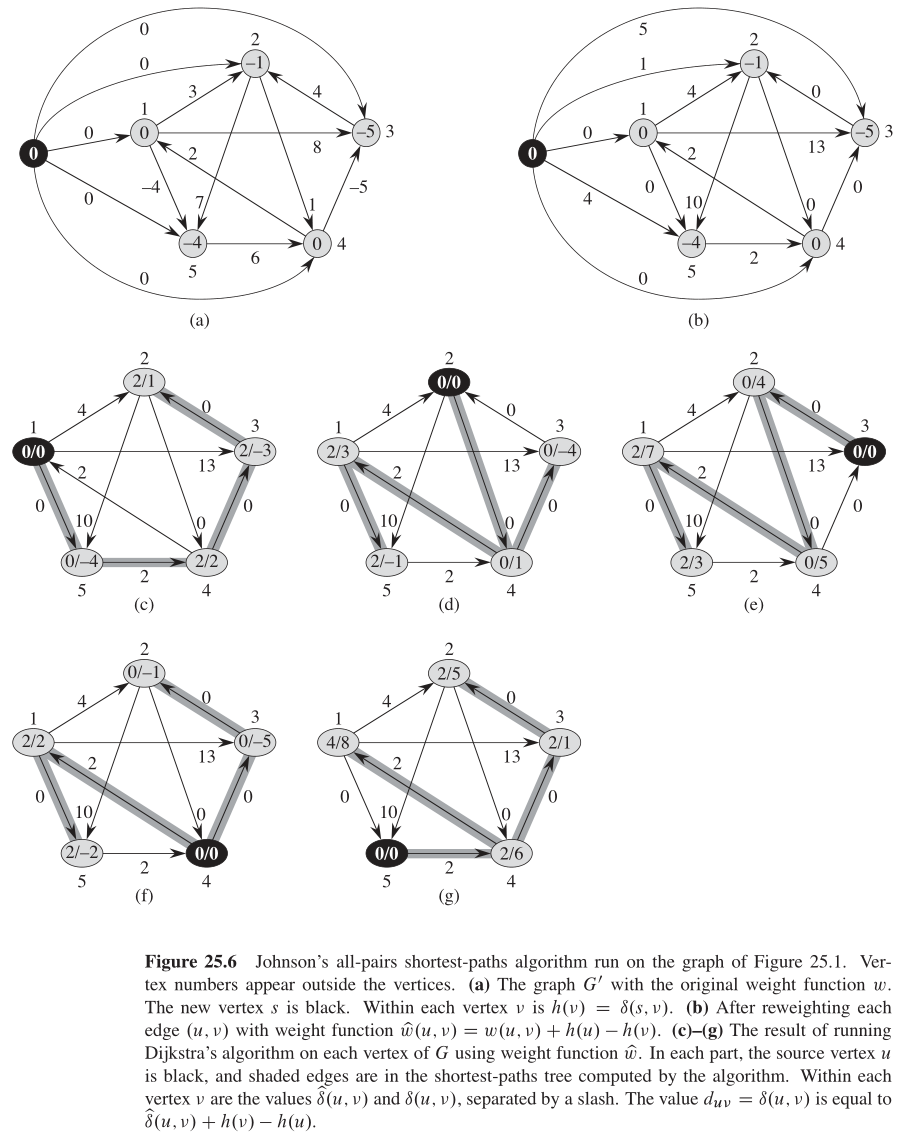
Johnson 算法的基本步骤如下：

重赋权图：为了能够使用高效的 Dijkstra 算法（要求边的权重非负），Johnson 算法使用重赋权技术，将图中可能存在的负权重边转换为非负权重边。
对每个结点运行 Dijkstra 算法：使用重赋权后的图，对每个结点运行一次 Dijkstra 算法，得到所有结点对之间的最短路径。
恢复原始权重：将重赋权后得到的最短路径转换回原始权重下的最短路径。

重赋权技术

重赋权技术基于以下观察：对于任意一条路径 p = <v₀, v₁, ..., vₖ>，它的原始权重与重赋权后的权重之间存在以下关系：

w'(p) = w(p) + h(v₀) - h(vₖ)

其中 w (p) 是原始权重，w'(p) 是重赋权后的权重，h 是一个从结点到实数的函数。

如果我们能找到合适的 h 函数，使得所有重赋权后的边权重 w'(u, v) = w (u, v) + h (u) - h (v) ≥ 0，那么我们就可以使用 Dijkstra 算法来求解最短路径问题。

为了找到这样的 h 函数，Johnson 算法引入了一个新的结点 s，并从 s 向所有其他结点添加一条权重为 0 的边。然后，以 s 为起点运行 Bellman-Ford 算法，计算出 h (v) = δ(s, v)，其中 δ(s, v) 是从 s 到 v 的最短路径权重。

算法流程

引入新的结点 s，向所有其他结点添加一条权重为 0 的边。
以 s 为起点运行 Bellman-Ford 算法，计算 h (v) = δ(s, v)。如果检测到负权回路，则算法终止。
对每条边 (u, v)，计算重赋权后的权重 w'(u, v) = w (u, v) + h (u) - h (v)。
对于每个结点 u，以 u 为起点，使用 Dijkstra 算法计算在重赋权图中从 u 到所有其他结点 v 的最短路径权重 δ'(u, v)。
恢复原始权重下的最短路径权重：δ(u, v) = δ'(u, v) + h (v) - h (u)。

代码实现

下面是 Johnson 算法的 C++ 实现：

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <algorithm>
using namespace std;// 边的结构
struct Edge {int to;     // 目标结点int weight; // 边的权重Edge(int t, int w) : to(t), weight(w) {}
};const int INF = INT_MAX / 2;  // 避免加法溢出// Bellman-Ford算法：计算从起点s到所有其他结点的最短路径
// 返回值：如果没有负权回路，返回true；否则返回false
bool bellmanFord(const vector<vector<Edge>>& graph, int s, vector<int>& dist) {int n = graph.size();dist.assign(n, INF);dist[s] = 0;// 松弛所有边n-1次for (int i = 0; i < n - 1; ++i) {for (int u = 0; u < n; ++u) {if (dist[u] == INF) continue;for (const Edge& e : graph[u]) {int v = e.to;int w = e.weight;if (dist[v] > dist[u] + w) {dist[v] = dist[u] + w;}}}}// 检测负权回路for (int u = 0; u < n; ++u) {if (dist[u] == INF) continue;for (const Edge& e : graph[u]) {int v = e.to;int w = e.weight;if (dist[v] > dist[u] + w) {return false;  // 存在负权回路}}}return true;
}// Dijkstra算法：使用优先队列优化，计算从起点s到所有其他结点的最短路径
void dijkstra(const vector<vector<Edge>>& graph, int s, vector<int>& dist) {int n = graph.size();dist.assign(n, INF);dist[s] = 0;// 优先队列：(距离, 结点)，按距离升序排列priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;pq.push({0, s});while (!pq.empty()) {int u = pq.top().second;int current_dist = pq.top().first;pq.pop();// 如果当前距离大于已知最短距离，跳过if (current_dist > dist[u]) continue;// 松弛所有邻边for (const Edge& e : graph[u]) {int v = e.to;int w = e.weight;if (dist[v] > dist[u] + w) {dist[v] = dist[u] + w;pq.push({dist[v], v});}}}
}// Johnson算法：计算所有结点对之间的最短路径
// 返回值：如果没有负权回路，返回true；否则返回false
bool johnson(const vector<vector<Edge>>& originalGraph, vector<vector<int>>& result) {int n = originalGraph.size();// 步骤1：创建新图，添加一个新的起点s（编号为n）vector<vector<Edge>> graph = originalGraph;graph.resize(n + 1);for (int i = 0; i < n; ++i) {graph[n].emplace_back(i, 0);  // 从s到所有其他结点添加一条权重为0的边}// 步骤2：以s为起点运行Bellman-Ford算法，计算h(v)vector<int> h;if (!bellmanFord(graph, n, h)) {return false;  // 存在负权回路}// 步骤3：构建重赋权后的图vector<vector<Edge>> reweightedGraph(n);for (int u = 0; u < n; ++u) {for (const Edge& e : originalGraph[u]) {int v = e.to;int w = e.weight;// 重赋权：w'(u, v) = w(u, v) + h(u) - h(v)reweightedGraph[u].emplace_back(v, w + h[u] - h[v]);}}// 步骤4：对每个结点运行Dijkstra算法，并恢复原始权重result.assign(n, vector<int>(n, INF));for (int u = 0; u < n; ++u) {vector<int> dist;dijkstra(reweightedGraph, u, dist);// 恢复原始权重：δ(u, v) = δ'(u, v) + h(v) - h(u)for (int v = 0; v < n; ++v) {if (dist[v] != INF) {result[u][v] = dist[v] + h[v] - h[u];}}}return true;
}// 打印所有结点对之间的最短路径矩阵
void printResult(const vector<vector<int>>& result) {int n = result.size();for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (result[i][j] == INF) {cout << "INF\t";} else {cout << result[i][j] << "\t";}}cout << endl;}
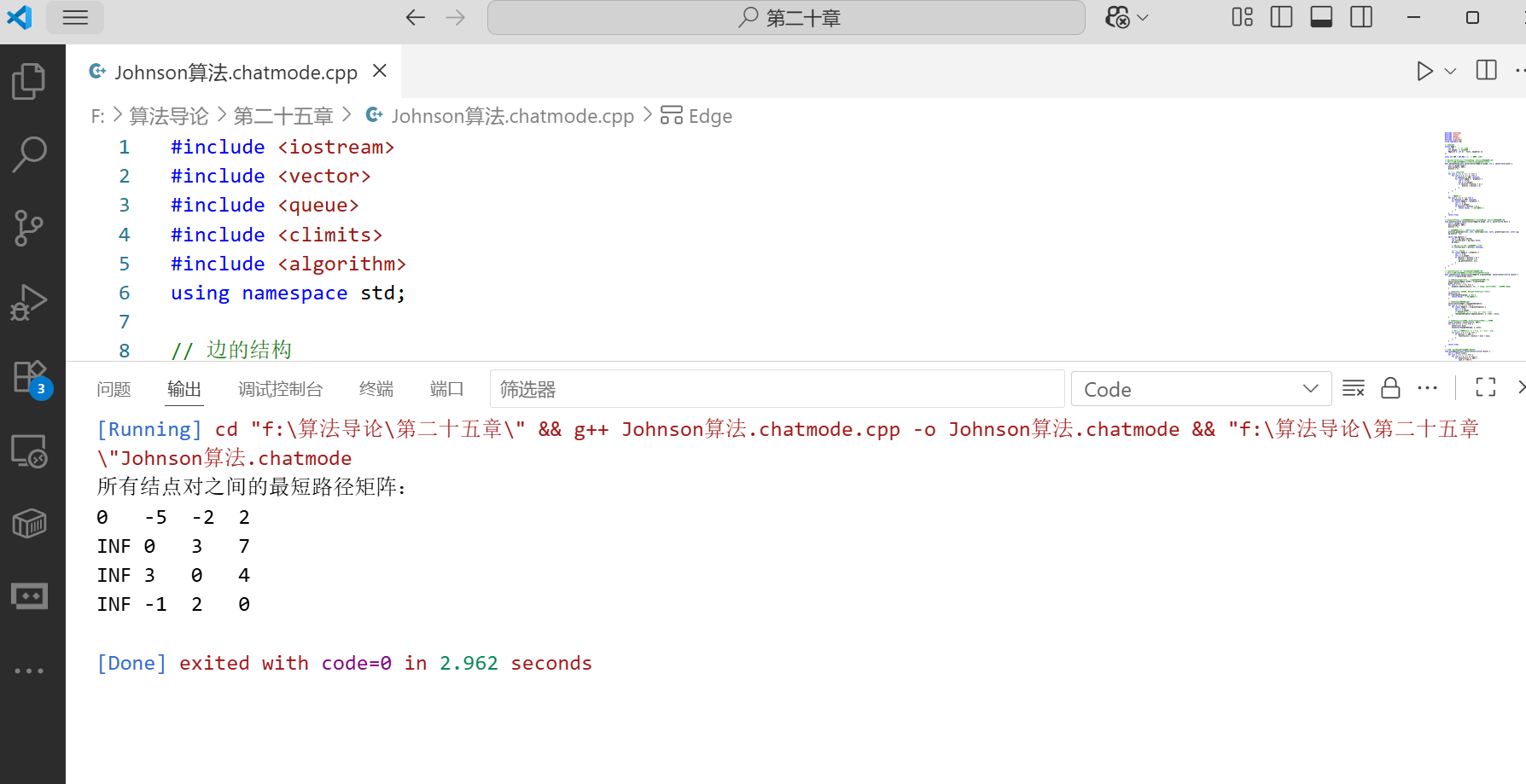
}int main() {// 示例图（稀疏图）int n = 4;vector<vector<Edge>> graph(n);// 添加边graph[0].emplace_back(1, -5);graph[0].emplace_back(2, 2);graph[1].emplace_back(2, 3);graph[2].emplace_back(3, 4);graph[3].emplace_back(1, -1);vector<vector<int>> shortestPaths;if (johnson(graph, shortestPaths)) {cout << "所有结点对之间的最短路径矩阵：" << endl;printResult(shortestPaths);} else {cout << "图中存在负权回路，无法计算最短路径" << endl;}return 0;
}

算法分析

时间复杂度：
- Bellman-Ford 算法的时间复杂度为 O (nm)，其中 n 是结点数，m 是边数
- 对每个结点运行一次 Dijkstra 算法（使用二叉堆实现），时间复杂度为 O (n (m log n))
- 总的时间复杂度为 O (nm + nm log n) = O (nm log n)
  对于稀疏图（m = O (n)），时间复杂度为 O (n² log n)，这比 Floyd-Warshall 算法的 O (n³) 更高效。
空间复杂度：O (n² + m)，用于存储图和所有结点对之间的最短路径矩阵。

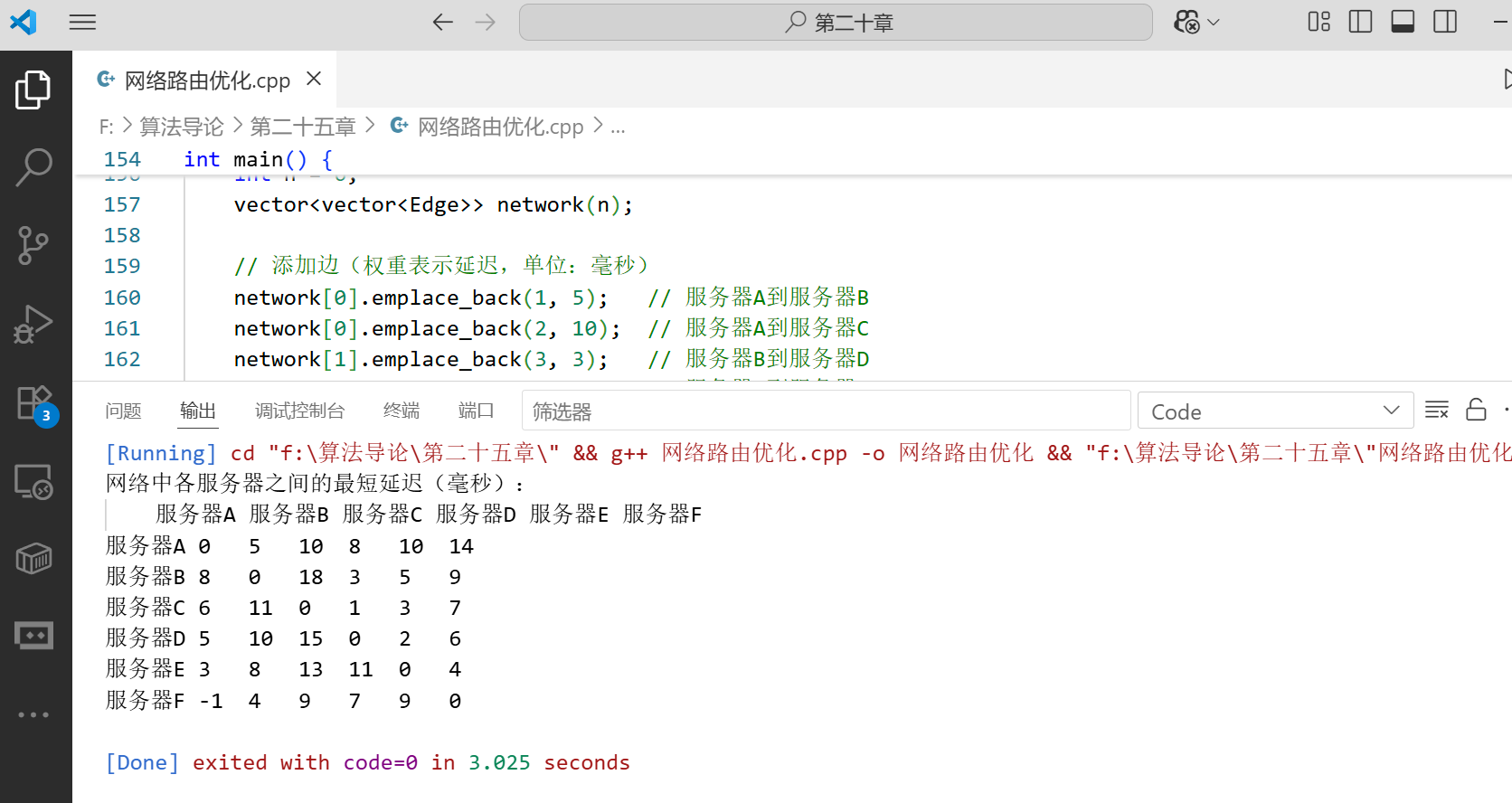
应用案例：网络路由优化

Johnson 算法特别适合处理稀疏图，如计算机网络中的路由问题。下面是一个网络路由优化的示例：

#include <iostream>
#include <vector>
#include <string>
#include <queue>
#include <climits>
using namespace std;// 定义无穷大常量，使用INT_MAX/2避免加法溢出
const int INF = INT_MAX / 2;// 网络节点名称
vector<string> nodes = {"服务器A", "服务器B", "服务器C", "服务器D", "服务器E", "服务器F"};// 边的结构
struct Edge {int to;int weight;Edge(int t, int w) : to(t), weight(w) {}
};// Bellman-Ford算法：计算从起点s到所有其他结点的最短路径
// 返回值：如果没有负权回路，返回true；否则返回false
bool bellmanFord(const vector<vector<Edge>>& graph, int s, vector<int>& dist) {int n = graph.size();dist.assign(n, INF);dist[s] = 0;// 松弛所有边n-1次for (int i = 0; i < n - 1; ++i) {for (int u = 0; u < n; ++u) {if (dist[u] == INF) continue;for (const Edge& e : graph[u]) {int v = e.to;int w = e.weight;if (dist[v] > dist[u] + w) {dist[v] = dist[u] + w;}}}}// 检测负权回路for (int u = 0; u < n; ++u) {if (dist[u] == INF) continue;for (const Edge& e : graph[u]) {int v = e.to;int w = e.weight;if (dist[v] > dist[u] + w) {return false;  // 存在负权回路}}}return true;
}// Dijkstra算法：使用优先队列优化，计算从起点s到所有其他结点的最短路径
void dijkstra(const vector<vector<Edge>>& graph, int s, vector<int>& dist) {int n = graph.size();dist.assign(n, INF);dist[s] = 0;// 优先队列：(距离, 结点)，按距离升序排列priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;pq.push({0, s});while (!pq.empty()) {int u = pq.top().second;int current_dist = pq.top().first;pq.pop();// 如果当前距离大于已知最短距离，跳过if (current_dist > dist[u]) continue;// 松弛所有邻边for (const Edge& e : graph[u]) {int v = e.to;int w = e.weight;if (dist[v] > dist[u] + w) {dist[v] = dist[u] + w;pq.push({dist[v], v});}}}
}// Johnson算法：计算所有结点对之间的最短路径
// 返回值：如果没有负权回路，返回true；否则返回false
bool johnson(const vector<vector<Edge>>& originalGraph, vector<vector<int>>& result) {int n = originalGraph.size();// 步骤1：创建新图，添加一个新的起点s（编号为n）vector<vector<Edge>> graph = originalGraph;graph.resize(n + 1);for (int i = 0; i < n; ++i) {graph[n].emplace_back(i, 0);  // 从s到所有其他结点添加一条权重为0的边}// 步骤2：以s为起点运行Bellman-Ford算法，计算h(v)vector<int> h;if (!bellmanFord(graph, n, h)) {return false;  // 存在负权回路}// 步骤3：构建重赋权后的图vector<vector<Edge>> reweightedGraph(n);for (int u = 0; u < n; ++u) {for (const Edge& e : originalGraph[u]) {int v = e.to;int w = e.weight;// 重赋权：w'(u, v) = w(u, v) + h(u) - h(v)reweightedGraph[u].emplace_back(v, w + h[u] - h[v]);}}// 步骤4：对每个结点运行Dijkstra算法，并恢复原始权重result.assign(n, vector<int>(n, INF));for (int u = 0; u < n; ++u) {vector<int> dist;dijkstra(reweightedGraph, u, dist);// 恢复原始权重：δ(u, v) = δ'(u, v) + h(v) - h(u)for (int v = 0; v < n; ++v) {if (dist[v] != INF) {result[u][v] = dist[v] + h[v] - h[u];}}}return true;
}// 打印网络节点间的最短路径
void printNetworkPaths(const vector<vector<int>>& result) {int n = result.size();cout << "\t";for (const string& node : nodes) {cout << node << "\t";}cout << endl;for (int i = 0; i < n; ++i) {cout << nodes[i] << "\t";for (int j = 0; j < n; ++j) {if (result[i][j] == INF) {cout << "INF\t";} else {cout << result[i][j] << "\t";}}cout << endl;}
}int main() {// 网络拓扑结构（稀疏图）int n = 6;vector<vector<Edge>> network(n);// 添加边（权重表示延迟，单位：毫秒）network[0].emplace_back(1, 5);   // 服务器A到服务器Bnetwork[0].emplace_back(2, 10);  // 服务器A到服务器Cnetwork[1].emplace_back(3, 3);   // 服务器B到服务器Dnetwork[2].emplace_back(3, 1);   // 服务器C到服务器Dnetwork[3].emplace_back(4, 2);   // 服务器D到服务器Enetwork[4].emplace_back(5, 4);   // 服务器E到服务器Fnetwork[5].emplace_back(0, -1);  // 服务器F到服务器A（模拟一条低延迟通道）vector<vector<int>> shortestPaths;if (johnson(network, shortestPaths)) {cout << "网络中各服务器之间的最短延迟（毫秒）：" << endl;printNetworkPaths(shortestPaths);} else {cout << "网络中存在异常链路（负权回路），无法计算最短路径" << endl;}return 0;
}

三种算法的比较

算法	时间复杂度	空间复杂度	适用场景	优点	缺点
基于矩阵乘法的算法	O(n³ log n)	O(n²)	稠密图，不含负权边	实现简单	效率较低，不适合处理负权边
Floyd-Warshall 算法	O(n³)	O(n²)	稠密图，可含负权边但不含负权回路	实现简单，可处理负权边，可检测负权回路	时间复杂度较高，不适合大型图
Johnson 算法	O(nm log n)	O(n² + m)	稀疏图，可含负权边但不含负权回路	对稀疏图效率高，可处理负权边	实现较复杂，需要结合 Bellman-Ford 和 Dijkstra 算法