顺序表 —— OJ题
在上一篇文章中简单介绍了顺序表,这一篇文章讲解下一个比较经典的题:
杨辉三角
先看一下什么是杨辉三角
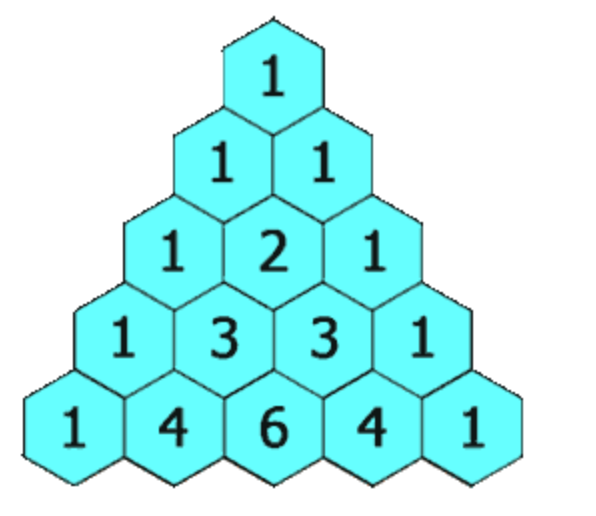
下面解释:
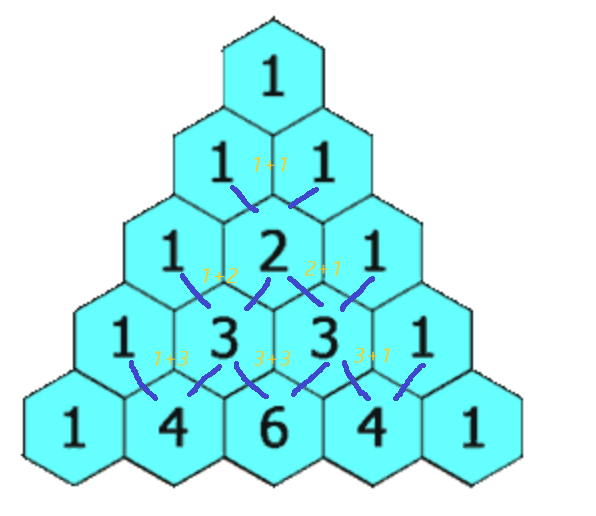
大概就是这个规律。而 ta 其实就是二维数组 即:
0 1
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1然后看一下这个题的要求:

意思是 numRows 一个非负数(整数),在根据 numRows 里的整数生成 【杨辉三角 】的“层数”
这是ta给的方法体:

这里的 List <List<Integer>>这个边讲边说
下面说一下 这道题如何解:
首先是步骤:
如果你仔细观察这个图就会发现 ta 的头值和尾值都是 1 而中间的都是运算来的
所以可以将这道题分为 头 中 尾 三部分处理
头 尾处理比较简单难点是 中 的处理,这时候 再仔细观察 中间的值,是如何得出来的,你会发现:
0 101 1 10 12 1 2 10 1 23 1 3 3 10 1 2 3 4 1 4 6 4 10 1 2 3 4所有的中间值都是由 上一个数组以下标 0 + 1 | 1 + 2 | 2 + 3
的规律得出下一个数组 1下标 2下标 3下标 的值 如4数组:1下标 = 1+3 、2下标 = 3 + 3 、3下标 = 3+1就可以这样写:
i = 数组
while(ture){
j = 0;
int val = i[j] + i[j+1];
j++;
}但这时候问题又出现了,以杨辉三角的规律不是那个数组,都有 1 2 3 下标的,这时候就要找条件
的要求了 这时候再仔细看一下图:
0 101 1 10 12 1 2 10 1 23 1 3 3 10 1 2 3 4 1 4 6 4 10 1 2 3 4会发现数组2需要加1次
数组3需要加2次
数组4需要加3次
后面相加的次数依次+1
只有 numRows 等于3时中间值需要加1次,4时加2次.......这个题最好用顺序表解决 下面看代码:
public List<List<Integer>> generate(int numRows) {List<Integer> list = new ArrayList<>();//List<List<Integer>> ta 的意思就是如果你存放数组(顺序表的底层是数组)的地址//会给这个地址放上 下标 ret是要返回的List<List<Integer>> ret = new ArrayList<>();//处理一层list.add(1);ret.add(list);//处理二层以上for(int i = 1; i<numRows; i++){//头List<Integer> cj = new ArrayList<>();cj.add(1);//中//这里的 get 拿的是数组的整个地址List<Integer> zo = ret.get(i-1);//只有numRows 为3及以上才会运算for(int j = 0; j<i-1; j++){int val = zo.get(j) + zo.get(j+1);cj.add(val);}//尾cj.add(1);ret.add(cj);}return ret;}List <List<Integer>>:
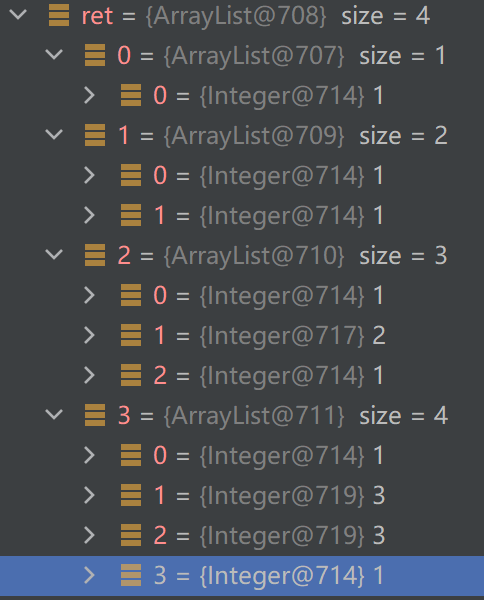
最后提交一下:
下一篇文章是 单向 无头 不循环链表
