当前位置： 首页 > news >正文

排序总结---保研机试极限复习

news 2025/8/16 4:40:56

目录

直接使用库函数排序

1.对数组升序排序

2.对数组降序排序

3.对vector升序排序

4.对vector降序排序

5.自定义结构体排序（Lambda表达式）

6.部分排序

手搓排序

1.快速排序

2.堆排序

 数组中的第K个最大元素

3.归并排序

4.插入排序（变体--折半插入 希尔排序）

5.冒泡排序

6.选择排序

直接使用库函数排序

1.对数组升序排序

#include <algorithm> // 必须包含的头文件int main() {int arr[] = {5, 3, 9, 1, 7};int n = sizeof(arr) / sizeof(arr[0]); // 计算数组长度// 默认升序排序（从小到大）std::sort(arr, arr + n); // 参数为指针范围：[arr, arr + n)// 输出结果：1 3 5 7 9return 0;
}

2.对数组降序排序

#include <algorithm>
#include <functional> // 需要包含此头文件以使用 greater<>int main() {int arr[] = {5, 3, 9, 1, 7};int n = sizeof(arr) / sizeof(arr[0]);// 使用 greater<int>() 降序排序std::sort(arr, arr + n, std::greater<int>());// 输出结果：9 7 5 3 1return 0;
}

3.对vector升序排序

#include <algorithm>
#include <vector>int main() {std::vector<int> vec = {5, 3, 9, 1, 7};// 默认升序排序std::sort(vec.begin(), vec.end()); // 参数为迭代器范围// 输出结果：1 3 5 7 9return 0;
}

4.对vector降序排序

#include <algorithm>
#include <vector>
#include <functional>int main() {std::vector<int> vec = {5, 3, 9, 1, 7};// 降序排序std::sort(vec.begin(), vec.end(), std::greater<int>());
//或者std::sort(vec.begin(), vec.end(), [](int a, int b) {return a > b;});// 输出结果：9 7 5 3 1return 0;
}

5.自定义结构体排序（Lambda表达式）

#include <iostream>
#include <vector>
#include <algorithm>struct Person {string name;int age;
};int main() {vector<Person> people = {{"Alice", 30}, {"Bob", 20}, {"Charlie", 25}};// 按年龄升序排序std::sort(people.begin(), people.end(), [](const Person& a, const Person& b) {return a.age < b.age;});return 0;
}

 Lambda 表达式允许在调用 std::sort 时直接定义比较逻辑，无需预先定义函数或重载运算符

Lambda 作为比较函数，返回 true 时第一个参数排在第二个参数之前

std::vector<int> nums = {5, 2, 9, 1};
std::sort(nums.begin(), nums.end(), [](int a, int b) {return a > b;  // 降序：a > b 时 a 排在前面
});
// 结果：9, 5, 2, 1

我们这样记忆，传入a和b 如果返回 a>b 大于号就代表前面的数大于后面的数，是降序排序

如果返回a<b，小于号就代表前面的数小于后面的数，升序排序 

模板

std::sort(students.begin(), students.end(), [](auto& a, auto& b) { ... });

 示例：先按成绩降序，成绩相同按名字升序（一般int 直接传值，string struct避免复制传引用）

struct Student { string name; int score; };vector<Student> students = {{"Alice", 85}, {"Bob", 90}, {"Charlie", 85}};std::sort(students.begin(), students.end(), [](const Student& a, const Student& b) {if (a.score != b.score) return a.score > b.score; // 成绩降序return a.name < b.name; // 名字升序
});
// 结果：Bob(90), Alice(85), Charlie(85)

6.部分排序

vector数组部分降序排序，部分排序记住左闭右开，右边要多加1

int main() {std::vector<int> vec = {9, 3, 6, 2, 8, 1};int start = 1, end = 4; // 排序索引 [1, 3] 的元素// 降序排序区间 [vec.begin()+1, vec.begin()+4]std::sort(vec.begin() + start, vec.begin() + end + 1, [](int a, int b) {return a > b;});// 输出：9 6 3 2 8 1for (int num : vec) {std::cout << num << " ";}return 0;
}
#include <iostream>
#include <vector>
#include <algorithm>int main() {vector<int> vec = {9, 3, 6, 2, 8, 1};int l = 1, r = 4; // 对索引 [1, 4] 区间排序// 对 vec[1]~vec[4] 升序排序std::sort(vec.begin() + l, vec.begin() + r + 1);return 0;
}

注意sort函数内部是快速排序，复杂度是nlogn 下面详细分析 

手搓排序

AcWing 787. 十大排序算法总结 - AcWing

75. 颜色分类 - 力扣（LeetCode）

下面按照重要性分析每个排序的1.手写代码 2.时间复杂度 3.稳定性  额外（一些排序算法的对比分析）

1.快速排序

AcWing - 算法基础课

快速排序（Quick Sort）是一种分治策略 的排序算法，其核心思想如下：

  • ​基准选择​：从数组中选取一个元素作为基准值（通常选择首元素、尾元素或随机元素）。
  • 分区​​：将数组分为两部分，使得左侧子数组的所有元素 ≤ 基准值，右侧子数组的所有元素 ≥ 基准值。基准值此时位于最终排序位置。
  • 递归排序​：对左右子数组递归执行上述过程，直到子数组长度为 1 或 0（天然有序）。

算法实现：

1.写好分治策略结束条件，也就是只剩一个数字， l<=r

2.确定基准元素 可以是第一个，最后一个，随机值，或者中间

3.核心算法，思想就是双指针，左边找到大于等于基准元素的值（一定要包括等于），右边找到小于等于的，然后如果此时左指针小于右指针，则交换。

4.递归，左指针左边和右指针右边才符合递归条件，所以记住递归条件一定包括左指针-1，右指针+1,这里还有一个重点就是，如果基准元素是选左边界，划分就要用右指针，如果基准元素是右边界，划分就用左指针

是因为对于第一次处理后的数组，索引i左侧的数字都是小于等于x，但不包括q[i]。索引i右侧的数字都是大于等于x，包括q[i]。故区间分为[l,i-1]和[i,r]。
同理，对于第一次处理后的数组，索引j左侧的数字都是小于等于x，包括q[j]。索引j右侧的数字都是大于等于x，不包括q[j]。故区间分为[l,j]和[j+1,r]。

再对x位置小结：

如果区间取[l,i-1]和[i,r]这种，那么x不应该取左边界(l、(l+r)/2)。
应取 x = q[r]; x = q[(l+r+1)/2];

如果区间取[l,j]和[j+1,r]这种，那么x不应该取右边界(如r、(l+r+1)/2)。
应取 x = q[l]; x = q[(l+r)/2];

自己选择其中一种即可。

5.用do while 因为每次交换完要往前进一步，否则如果两个数相同会陷入死循环，所以一开始要让i=left-1 j=right+1

#include <iostream>
using namespace std;
const int N=1e5+10;
int a[N];
void quick_sort(int a[N],int l,int r){if(l>=r)return ;int i=l-1,j=r+1,x=a[(l+r+1)/2];while(i<j){do i++;while(a[i]<x);do j--;while(a[j]>x);if(j>i)swap(a[i],a[j]);}quick_sort(a,l,i-1);quick_sort(a,i,r);}int main(){int n;cin>>n;for(int i=0;i<n;i++)cin>>a[i];quick_sort(a,0,n-1);for(int i=0;i<n;i++)cout<<a[i]<<" ";return 0;
}

复杂度分析：

注意最好情况和平均情况一样，二分，深度为​log₂n，但是最差情况就是每一次你的基准元素都在最边上，所以每次是n n-1 ……。然后每层遍历n个元素都是一样的

平均与最优情况：O(n log n)​​

  • ​原因​：每次划分将数组均匀分成两半（比例接近 1:1），递归深度为 ​log₂n，每层需遍历 ​O(n)​​ 元素。

​ 最坏情况：O(n²)​​

  • ​触发场景​：每次划分极不平衡（如数组已有序且固定选首元素为基准）。
  • ​原因​：递归深度退化为 ​n，每层操作数依次为 ​n, n-1, ..., 1​（等差数列求和公式：​ΣO(i) = O(n²)​

不稳定，遍历的时候相同的值在左指针被遍历到就会到右边去，右指针遍历到就会往左边去

786. 第k个数 - AcWing题库

2.堆排序

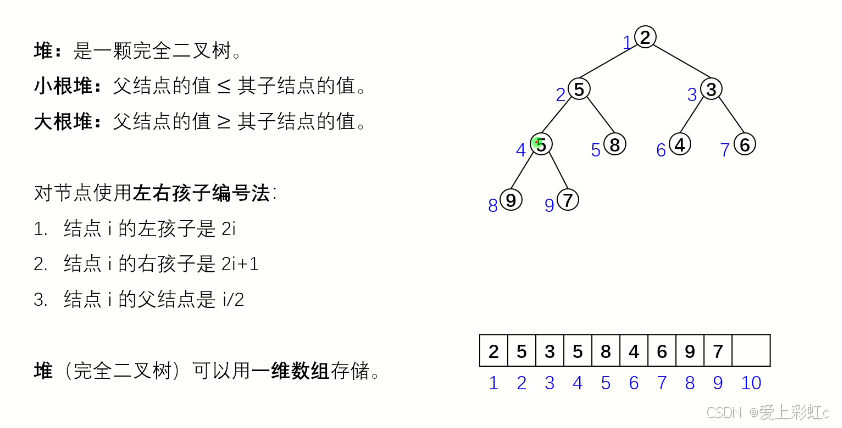
堆排序是基于堆这种数据结构的，堆是一棵完全二叉树（不一定是满二叉树）

大根堆：

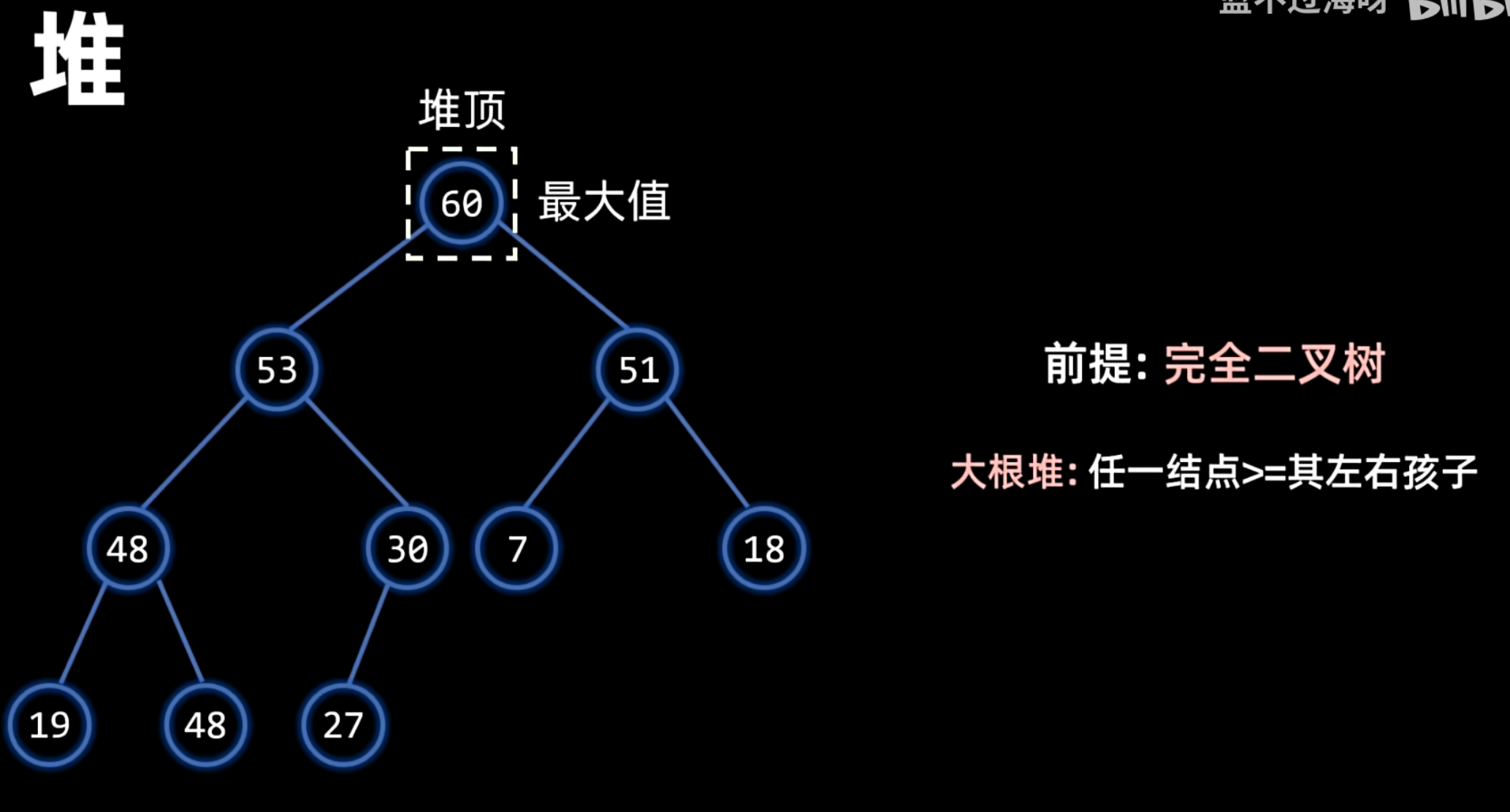
小根堆：

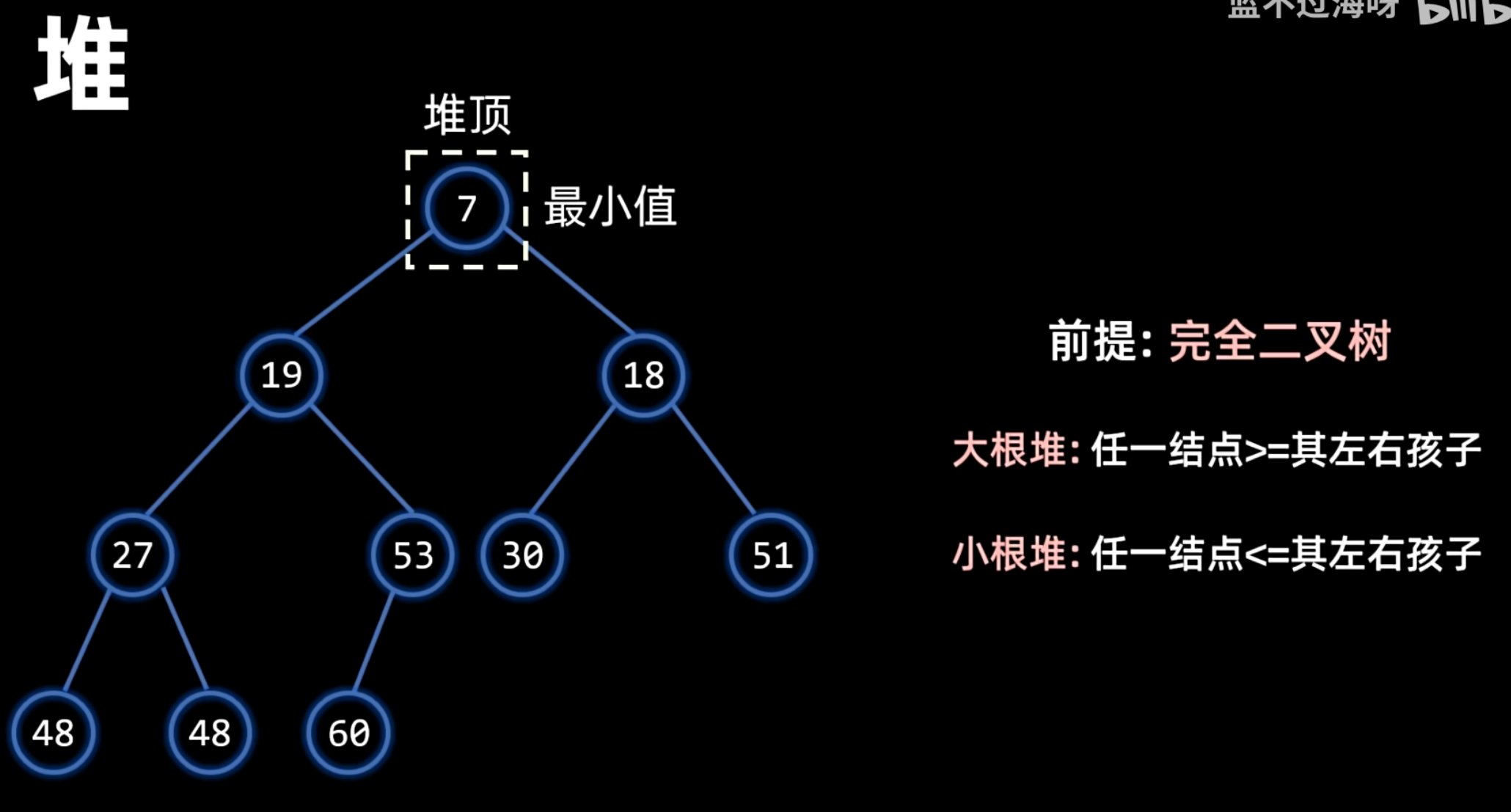
堆的存储：由于这是一颗完全二叉树，是连续结构，适合用数组来顺序存储，（一般从下标1开始存储） ，因为从1开始会符合某种性质

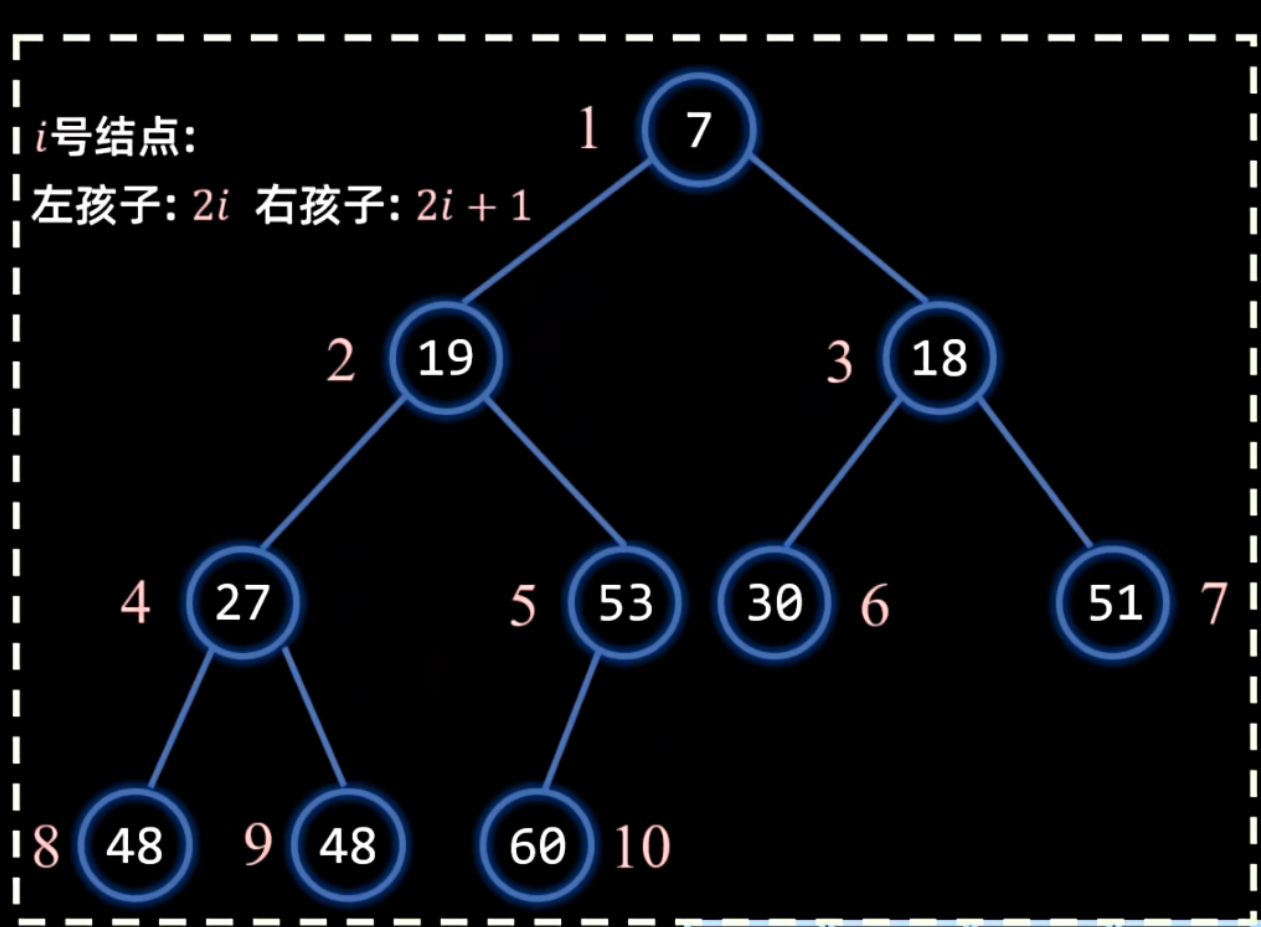
排序思想
1.首先将待排序的数组构造成一个大根堆，此时，整个数组的最大值就是堆结构的顶端
⒉将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1
3.将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组
注意:升序用大根堆，降序就用小根堆(默认为升序)

如何构造堆？

利用下沉操作，就是从最后一个非叶子节点开始，一直到第一个节点，依次进行下沉操作，下沉就是不断和下面两个元素比较交换

最后一个非叶子节点的下标，要看你的数组是从0开始还是从1开始，在草稿纸上画一下很容易判断

        int n =nums.size();n=n-1;//建堆，此时堆长度为 0-n-1for(int i=(n-1)/2;i>=0;i--){down(nums,i,n);}

如何排序？

构造好堆后，将第一个元素交换到末尾，此时末尾元素就已经排好序了，然后再继续下沉，但是注意，要把最后一个元素剔除在外

        //排序//将前k-1个元素放到最后排好序，此时堆顶元素就是第k大元素k=k-1;while(n>=0&&k--){swap(nums[0],nums[n]);n--;down(nums,0,n);}

下沉操作如何实现？

    void down(vector<int>& nums,int u,int r){int t=u;if(u*2+1<=r&&nums[u*2+1]>nums[t]) t=u*2+1;if(u*2+2<=r&&nums[u*2+2]>nums[t]) t=u*2+2;if(u!=t){swap(nums[u],nums[t]);down(nums,t,r);}}

首先找到左右节点的最小值（需要先判断左右节点存不存在），然后交换，如果交换操作发生了，那么从这个点开始继续下沉，直到交换操作没发生，如果下沉到左右节点不存在，交换操作当然也不会发生，那么就会退出递归，这个模板记一下，下面是整体使用（从1开始）

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 100010;int a[N];//保存数组
int n, m;//n个点，求前m小
int r ;//堆得右边界
void down(int u)//调整函数
{//t记录最小点的编号int t = u;//有左儿子，并且左儿子比t节点的值小，更新tif(2 * u <= r && a[2 * u] < a[u]) t = 2 * u;//有右儿子，并且右儿子比t节点的值小，更新tif(2 * u + 1 <= r && a[2 * u + 1] < a[t]) t = 2 * u + 1;//如果待调整点不是最小的if(u != t){//和最小的交换swap(a[u], a[t]);//递归处理down(t);}
}int main()
{cin >> n >> m;r = n;//开始时，右边界是数组边界//读入数据for (int i = 1; i <= n; i ++ ){cin >> a[i];}//从第一个非叶节点开始，从右到左，从下到上处理每个节点for(int i = n /2 ; i >= 1; i--){down(i);}//输出m个最小值while (m -- ){//堆顶保存的最小值，输出堆顶cout << a[1] << " ";//将堆顶和右边界交换swap(a[1], a[r]);//右边界左移r--;//从新处理堆顶down(1);}
}

复杂度分析：

排序过程，每一个堆顶元素都要从头换到尾部，一共（n-1）轮，每一轮都要从顶到底比较交换，log（n）；

由于前面的数会先被移动到尾部，所以是不稳定的。

 数组中的第K个最大元素

215. 数组中的第K个最大元素 - 力扣（LeetCode）

3.归并排序

归并排序是稳定的分治排序算法，将数组分成两半，分别排序后再合并。

- 分治策略：递归地将数组分成两半

- 合并操作：将两个有序数组合并成一个有序数组

- 时间复杂度：O(n log n)

- 空间复杂度：O(n)

 算法实现步骤

1. **分解**：将数组分成两个子数组

2. **递归排序**：对两个子数组分别进行归并排序

3. **合并**：将两个有序子数组合并成一个有序数组

分解 就是mid 递归排序就是两个递归调用 合并就是双指针

#include <iostream>
using namespace std;
int n;
const int N=1e5+10;
int nums[N];void merge_sort(int nums[N],int l,int r)
{if(l>=r) return ;int mid=(l+r)/2;merge_sort(nums,l,mid);merge_sort(nums,mid+1,r);int i=l;int j=mid+1;int tmp[N];int k=0;while(i<=mid&&j<=r){if(nums[i]<nums[j]){tmp[k++]=nums[i++];}else{tmp[k++]=nums[j++];}}while(i<=mid)tmp[k++]=nums[i++];while(j<=r)tmp[k++]=nums[j++];for(int i=l,j=0;i<=r;i++,j++){nums[i]=tmp[j];}return ;}int main()
{cin>>n;for(int i=0;i<n;i++){cin>>nums[i];}merge_sort(nums,0,n-1);for(int i=0;i<n;i++){cout<<nums[i]<<" ";} return 0;
}

AcWing - 算法基础课

AcWing - 算法基    础课

4.插入排序（变体--折半插入 希尔排序）

插入排序通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入

.5333. 插入排序 - AcWing题库1

1.直接插入

### 算法实现步骤

1. **从第二个元素开始**：假设第一个元素已排序

2. **取出当前元素**：保存待插入的元素

3. **向前扫描**：在已排序序列中找到插入位置

4. **移动元素**：将大于待插入元素的元素后移

5. **插入元素**：将待插入元素放到正确位置

class InsertionSort {
public:void insertionSort(vector<int>& nums) {int n = nums.size();// 从第二个元素开始插入for (int i = 1; i < n; i++) {int key = nums[i];  // 待插入的元素int j = i - 1;      // 已排序部分的最后一个元素// 向前扫描，找到插入位置while (j >= 0 && nums[j] > key) {nums[j + 1] = nums[j];  // 元素后移j--;}// 插入元素nums[j + 1] = key;}}
};

折半插入--在插入排序的基础上，使用二分查找来寻找插入位置，减少比较次数。

注意使用二分查找之前，先判断一下是不是可以直接放在这个位置，如果可以的话就跳过这一轮二分

#include<iostream>
using namespace std;int n;
const int N=1e3+10;
int nums[N];int Binary_Search(int nums[N],int l,int r,int key)
{if(r==l) return nums[r]<=key;while(l<r){int mid=(l+r)/2;if(nums[mid]>=key) r=mid;else l=mid+1;}return l;}void insert_sort(int nums[N])
{for(int i=1;i<n;i++){int key=nums[i];if(key>nums[i-1]) continue;int pos=Binary_Search(nums,0,i-1,key);for(int j=i-1;j>=pos;j--){nums[j+1]=nums[j];}nums[pos]=key;}}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{cin>>nums[i];
}insert_sort(nums);    for(int i=0;i<n;i++){cout<<nums[i]<<" ";}return 0;
}

5.冒泡排序

冒泡排序重复地遍历要排序的数列，比较相邻元素并交换位置，使较大的元素逐渐"冒泡"到数列的末尾。

**核心思想：**

- 相邻比较：比较相邻的两个元素

- 交换位置：如果顺序错误就交换

- 重复过程：每轮确定一个最大值的位置

- 时间复杂度：O(n²)

### 算法实现步骤

1. **外层循环**：控制排序轮数，每轮确定一个最大值

2. **内层循环**：进行相邻元素的比较和交换

3. **优化**：如果某轮没有发生交换，说明已经有序

#include <iostream>
using namespace std;int n;
const int N=1e3+10;
int nums[N];void bubble_sort(int nums[N])
{for(int i=0;i<n;i++){bool swapped=false;for(int j=0;j<n-i-1;j++){if(nums[j]>nums[j+1]){swap(nums[j],nums[j+1]);swapped=true;}}if(!swapped) break; }}int main()
{cin>>n;for(int i=0;i<n;i++){cin>>nums[i];}bubble_sort(nums);for(int i=0;i<n;i++){cout<<nums[i]<<" ";}return 0;
}

5334. 冒泡排序 - AcWing题库

6.选择排序

  • 步骤1​：从未排序序列中找到最小（或最大）元素。
  • ​步骤2​：将该元素与未排序序列的起始元素交换位置。
  • ​步骤3​：将交换后的起始元素视为已排序部分，剩余部分作为新的未排序序列。
  • ​重复​：重复上述步骤，直至所有元素排序完成
#include <iostream>
using namespace std;int n;
const int N=1e3+10;
int nums[N];void choose_sort(int nums[N])
{for(int i=0;i<n-1;i++){int k=i;for(int j=i+1;j<n;j++){if(nums[k]>nums[j]){k=j;}}swap(nums[i],nums[k]);  }}int main()
{cin>>n;for(int i=0;i<n;i++){cin>>nums[i];}choose_sort(nums);for(int i=0;i<n;i++){cout<<nums[i]<<" ";}return 0;
}

5332. 选择排序 - AcWing题库

http://www.dtcms.com/a/329342.html

相关文章：

  • 亚马逊聚焦战略2.0：从资源分散到价值聚焦的商业重构逻辑
  • 北京JAVA基础面试30天打卡09
  • Java面试宝典：ZGC
  • 【自动化运维神器Ansible】playbook主机清单变量深度解析：主机变量与组变量的实战应用
  • InfluxDB数据恢复
  • 在JVM跑JavaScript脚本 | Oracle GraalJS 简介与实践
  • MySQL数据库核心操作解析
  • 数据库基础—SQL语句总结及在开发时
  • 如何使用 Ollama 在本地设置并运行 Qwen3
  • 2025年高效能工程项目管理软件推荐榜单：AI重构工程进度可视化与资源动态调度体系
  • 【国内电子数据取证厂商龙信科技】RAID存储技术
  • Spring Boot 集成 机器人指令中枢ROS2工业机械臂控制网关
  • Linux系统之K8S基本命令概述
  • PyTorch基础(Numpy与Tensor)
  • 集成 OceanBase 并打印 SQL 日志
  • 老生常谈智能指针：《More Effective C++》的条款28
  • PCIe Base Specification解析（十一）
  • nginx高性能web服务器实验
  • 【114页PPT】基于SAPSRM数字化采购解决方案（附下载方式）
  • Java面试宝典：G1垃圾收集器下
  • hadoop 前端yarn查看
  • 完整源码+技术文档！基于Hadoop+Spark的鲍鱼生理特征大数据分析系统免费分享
  • 以太坊的下一个十年：Vitalik Buterin的愿景与挑战
  • Day51--图论--99. 岛屿数量（卡码网），100. 岛屿的最大面积（卡码网）
  • 互联网大厂Java求职面试实录：Spring Boot到微服务与AI的技术问答
  • day50 图论基础 卡码网98. 所有可达路径
  • Day52--图论--101. 孤岛的总面积（卡码网），102. 沉没孤岛（卡码网），103. 水流问题（卡码网），104. 建造最大岛屿（卡码网）
  • java学习 leetcode 二分查找 图论
  • 【25-cv-09259】Keith律所代理Macneil Studio发起TRO狙击！
  • AI产品：从功能固化到动态进化