注意力机制进化史：从MHA到MoBA，新一代注意力机制的极限突破！

DeepSeek 发布了一篇新论文，提出了一种改进版的注意力机制 NSA，即Native Sparse Attention，可以直译为「原生稀疏注意力」；但其实就在同一天，月之暗面也发布了一篇主题类似的论文，提出了一种名为 MoBA 的注意力机制，即 Mixture of Block Attention，可以直译为「块注意力混合」。

与 DeepSeek 的 NSA 注意力机制新论文一样，月之暗面这篇 MoBA 论文也收获了诸多好评，借此笔者回顾了一些注意力机制相关模型：从MHA、MQA、GQA、MLA到NSA、MoBA

背景知识

MLA主要通过优化KV-cache来减少显存占用，从而提升推理性能。直接抛出这个结论可能不太好理解。首先我们来看下，对于生成模型，一个完整的推理阶段是什么样的，推理性能上有什么问题。这部分内容主要来自：

deepseek技术解读(1)-彻底理解MLA（Multi-Head Latent Attention） https://zhuanlan.zhihu.com/p/16730036197

LLM模型推理过程

LLM推理分为两个阶段：prefill阶段和decode阶段

• prefill阶段：是模型对全部的Prompt tokens一次性并行计算，最终会生成第一个输出token
• decode阶段：每次生成一个token，直到生成EOS（end-of-sequence）token，产出最终的response

在推理过程中，由于模型堆叠了多层transformer，所以核心的计算消耗在Transformer内部，包括MHA，FFN等操作，其中MHA要计算Q，K ，V 矩阵，来做多头注意力的计算。

在LLM生成过程中，是一个基于前向序token列预测下一个token的过程，序列中的token（无论是prefill阶段，还是decode阶段）只与它前面的token交互来计算attention，我们也称这种Attention为Causal Attention。矩阵计算上通过一个下三角的Causal Attention Mask来实现token交互只感知前向序列。如图1所示，展现的Transformer内部的细节：

图片来源:https://zhuanlan.zhihu.com/p/16730036197

我们以一个序列的 $t$ 位置的 token 为例，计算一层 Transformer 的 attention 过程，如列下公式所示：

$$\begin{array}{rl}[q_{t,1},q_{t,2},\dots ,q_{t,n}]& =q_t,\\ [k_{t,1},k_{t,2},\dots ,k_{t,n}]& =k_t,\\ [v_{t,1},v_{t,2},\dots ,v_{t,n}]& =v_t,\\ o_{t,i}& =\sum _j\text{Softmax}\left(\frac{q_{t,i}{k}_{j,i}^T}{\sqrt{d_k}}\right)v_{j,i},\\ o_t& =W^o[o_{t,1},o_{t,2},\dots ,o_{t,n}].\end{array}$$

DeepSeek-V3 中的 Attention 计算公式

公式中的符号：

$t$ 表示计算序列中第 $t$ 个 token；$q,k,v,o$ 中的两个下标，前一个表示 token 位置，后一个表示对应的 Head 下标。

从公式 $(7)$ 可以看到，在计算 Attention 时，$t$ 位置的 $q$ 只与 $t$ 位置前的 $k,v$ 做计算，所以我们有如下两个结论：

1. 计算前面的 $k,v$ 并不受后面 token 的影响。
2. 后面计算 $t+1,t+2,\dots ,t+n$ 位置的 Attention，要使用前序的 $1\to t$ 位置的 $k,v$ 的信息且始终不变的。

所以为了加速训练和推理的效率，在 token-by-token 生成过程中，避免重复计算前序的 $k,v$。研究者们引入缓存机制，将计算好的 $k,v$ 存在缓存，这也就是目前主流的 KV-cache 机制。KV-cache 的本质是换取空间换时间的方法。我们知道当前 LLM 还是比较大，GPU 的显存空间也是比较宝贵的，通过将有限长的 KV-cache 作为公用来节约存储空间。换句话说，如果不使用 KV-cache 模型在推理计算时（重复计算前序 $k,v$），是个计算密集型任务；增加了 KV-cache 机制，现在 $k,v$ 不再是过时计算得出，而是从「存储点」直接拿来算，GPT 格式存储合适的数据格式后又引入类似数据库管理任务。所以使用了 KV-cache 的机制，解决的就是重复计算的问题，间接的也就提升了推理或训练的速度。

访存速率分级

为了直观理解访存的速率，我们以一个分布式推理架构为例。

比如2台机器，每台机器有8张A100， 那么在这样一个系统内，卡内，单机卡间，机器之间的数据访问效率如图3所示。
注：我们的例子中，只描述了一种访存介质HBM (也就是我们常说的显卡的显存)，我们知道通常GPU的存储介质除了显存，还有SRAM和DRAM。SRAM也被成为片上存储，是GPU计算单元上即时访问更快的存储，所有的计算都要先调度到片上存储SRAM才能做计算，一般只有几十M大小，带宽可达到20T/s左右，SRAM是跟计算单元强绑定的，推理阶段一般不考虑将SRAM作为存储单元使用。而DRAM是我们常说的CPU的内存，由于访问速率较慢，推理阶段一般也不考虑使用。所以我们讨论的推理存储介质，一般就指的是HBM（显存）

分布式推理架构卡内、卡间、跨机存储和带宽

由上图的访存带宽可知，卡内的带宽是单机卡间的带宽的3倍，是跨机带宽的20倍，所以我们对于存储的数据应该优先放到卡内，其次单机内，最后可能才考虑跨机存储。

接下来我们再看下，推理过程中，有哪些数据要存储到显存上。

模型推理阶段显存分配

推理阶段主要有三部分数据会放到显存里。

• KV Cache ： 如上一节所述，前序token序列计算的$k,v$结果，会随着后面tokent推理过程逐步存到显存里。存储的量随着Batch，Sequence_len长度动态变化
• 模型参数：包括Transformer、Embedding等模型参数会存到显存里。模型大小固定后，这个存储空间是固定的。
• 运行时中间数据： 推理过程中产出的一些中间数据会临时存到显存，即用即释放，一般占用空间比较小

由上述可知，推理阶段主要存储消耗是两部分： 模型参数和 KV Cache。那么模型参数占多少，KV Cache又占多少？

首先我们先以一个token的计算过程为例，看下一个token计算要存储多少KV？为了方便理解，我们以Qwen-72B模型为例，模型配置详见： Qwen-72B-Chat。

模型共80层，每层有64个Head，每个Head的向量维度是128，
$$l=80,nh=64,dh=128$$
注：这里先不考虑qwen 72B GQA的设置（实际上KV做了压缩处理），只考虑当前模型的MHA的模型结构（假设不做任何处理），GQA后面再详细讨论。

如下图所示，计算一个token，每个Transformer层的每个Head都需要存储一对$k$, $v$。

单token kv缓存数据,来源https://zhuanlan.zhihu.com/p/16730036197

所以针对一个token，缓存的k，v数据总量是：

$$nu{m}_{kv}=2\ast k\ast l\ast n_h=2\times (80\times 64{)}_{qwe{n}_{72B}}=10240(1)$$

其中公式中的k表示1个k和1个v，一个token就需要存10240个k，v，这个数是不是有点离谱之外！那么k，v占多少存储呢？我们使用模型推理时会是半精度（bf16）参数，每个参数占2Byte。最长一个token的存储量，如公式(2)计算所示：

$$1toke{n}_{mem}=2\ast nu{m}_{kv}\ast d_h=2\times (10240\times 128{)}_{qwe{n}_{72B}}=2.62(MB)(2)$$

我们现在在计算一个Token计算需要存储的k，v数量和存储量。那么对于一个实际的推理场景，还需要考虑批量Batch (B) 和序列长度Sequence_len(S)两个维度，来估计整体KV Cache的存储需求。随着两个维度增大时可以动态变化的。我们看看下面两种场景：
场景1：单条短文本场景

Batch和序列设置：B = 1, S = 2048。此时k，v cache总量是：

$$me{m}_{kv}=1toke{n}_{memkv}\ast B\ast S=(2.62(MB)\times 1\times 2048{)}_{qwe{n}_{72B}}=5.366GB(3)$$

场景2：并发长文本场景

Batch和序列设置：B = 32, S = 4096。此时k，v cache总量是：

$$me{m}_{kv}=1toke{n}_{memkv}\ast B\ast S=(2.62(MB)\times 32\times 4096{)}_{qwe{n}_{72B}}=343.4GB(4)$$

除了k，v 消耗存储空间时，我们还通过模型参数数量占用的存储，推理阶段模型参数占用的存储空间是固定的，可以忽略模型参数数量*B；其中，bf16精度做推理，则参数是2Φ(Byte)，也还是以qwen-72B为例，参数占用存储空间：

$$me{m}_p=2\ast \Phi =2\times (72{)}_{qwe{n}_{72B}}=144G(5)$$

我们将结合上面两个场景，看查看存储的整体分布：

• 场景1：模型推理需要mem_p = 144G，kv存储memkv = 5.366GB，，模型的参数储存占主导，使用80G的A100， 至少需要2张卡做推理。
• 场景2：模型推理需要mem_p = 144G，kv存储memkv = 343.4GB，，KV Cache储存占主导，使用80G的A100， 至少需要7张卡做推理。

这里还要多啰嗦几句，推理阶段根据离线、在线的业务场景，到底组多大的Batch，其实是一个Balance的过程，Batch选择比较小，虽然并发度不高，但可能单卡就能装下完整模型参数和KV Cache，这时候卡内带宽会比较高，性能可能依然出众，可以考虑适当增加Batch把单卡显存用满，进一步提升性能。但当Batch再增大，超出单卡范围、甚至超出单机范围，此时并发会比较大，但跨卡或跨机访存性能会降低，导致访存成为瓶颈，GPU计算资源使用效率不高，可能实际导致整体推理性能不高。所以单从推理Batch设置角度来看，要实测找到性能最佳的平衡点。

当前LLM都比较大，而访存的容量和访存速率有分级的特点。所以推理过程中，减少跨卡、卡机的访存读写是优化推理性能的一个有效路径。一方面单次读写的数据越少，整体速度会越快；另一方面整体显存占用越少，就能尽量把数据放到单卡或单机上，能使用更高的带宽读写数据。

解码中的KV Cache

我们下面用一个例子更加详细的解释什么是KV Cache，了解一些背景的计算问题，以及KV Cache的概念。

无论是encoder-decoder结构，还是现在我们最接近AGI的decoder-only的LLM，解码生成时都是自回归auto-regressive的方式。也就是说，解码的时候，先根据当前输入 $inpu{t}_{i-1}$，生成下一个token，然后把生成的token拼接在 $inpu{t}_{i-1}$ 后面，获得新的输入 $inpu{t}_i$，再用 $inpu{t}_i$ 生成 $toke{n}_{i+1}$，依此选择，直到生成结果。

比如我们输入“窗前明月光下一句是”，那么模型每次生成一个token，输入输出会是这样（方便起见，默认每个token都是一个字符）

step0: 输入=[BOS]窗前明月光下一句是；输出=疑
step1: 输入=[BOS]窗前明月光下一句是疑；输出=是
step2: 输入=[BOS]窗前明月光下一句是疑是；输出=地
step3: 输入=[BOS]窗前明月光下一句是疑是地；输出=上
step4: 输入=[BOS]窗前明月光下一句是疑是地上；输出=霜
step5: 输入=[BOS]窗前明月光下一句是疑是地上霜；输出=[EOS]

(其中[BOS]和[EOS]分别是开始和结束的标记字符)

我们看一下在计算的过程中，如何输入的token “是” 的最后是hidden state如何传递到后面的类Token预测模型，以及后面每一个token，使用新的输入列中最后一个时刻的输出。

我们可以看到，在每一个step的计算中，主要包含了上一轮step的内容，而且只在最后一步使用（一个token）。那么每一个计算也就包含了上一轮step的计算内容。

从公式来看是这样的，回想一下我们attention的计算：

$${\alpha }_{i,j}=\text{softmax}(q_i{k}_j^T)$$

$$o_i=\sum _{j=0}^i{\alpha }_{i,j}{v}_{ij}$$

注意对于decoder的时候，由于mask attention的存在，每个输入只能看到自己和前面的内容，而看不到后面的内容。

假设我们当前输入的长度是3，预测第4个字，那么每层attention所做的计算有：

$$o_0={\alpha }_0,0v_0$$

$$o_1={\alpha }_{1,0}{v}_0+{\alpha }_{1,1}{v}_1$$

$$o_2={\alpha }_{2,0}{v}_0+{\alpha }_{2,1}{v}_1+{\alpha }_{2,2}{v}_2$$

预测完第4个字，放到输入里，继续预测第5个字，每层attention所做的计算有：

$$o_0={\alpha }_{0,0}{v}_0$$

$$o_1={\alpha }_{1,0}{v}_0+{\alpha }_{1,1}{v}_1$$

$$o_2={\alpha }_{2,0}{v}_0+{\alpha }_{2,1}{v}_1+{\alpha }_{2,2}{v}_2$$

可以看到，在预测第5个字时，只有最后一步引入了新的计算，而 $o_0$ 到 $o_2$ 的计算部分是完全重复的。

但是模型在推理的时候可不管这些，无论你是否只是要最后一个字的输出，它都会把所有输入计算一遍，给出所有输出结果。

也就是说中间有很多我们不需要的计算，这样就造成了浪费。

而且随着生成的结果越来越多，输入的长度也越来越长，上面这个例子里，输入长度是step0的10个， 每步骤，直接step5到15个。如果输入的instruction是规范型任务，那么可能有800个step。这个情况下，step0就变得有800次，step1被重复了799次——这样浪费的计算资源显然不可忍受。

有没有什么方法可以重利用上一个step里已经计算过的结果，减少浪费呢？

答案就是KV Cache，利用一个缓存，把需要重复利用的时序计算结果保存下来，减少重复计算。

而 $K$ 和 $V$ 就是需要保存的对象。

想一想，下图就是缓存的过程，假设我们第一次输入的输入长度是3个，我们第一次预测输出预测第4个字，那么由于下图给你看的是每个输入步骤的缓存，每个时序步骤都需要存储一次，而我们依旧会有些重复计算的情况。则有：

kv_cache下标l表示模型层数。在进行第二次预测时，也就是预测第5个字的时候，在第l层的时候，由于前面我们缓存了每层的$k$, $v$值，那层就不需要算新的$o_3$，而不再算$o_1$, $o_2$。因为第l层的$o_0$, $o_1$ 本来经过FFN层之后进到$l+1$层，再经过新的投影变换，成为$l+1$层的$k$, $v$值，但是是$l+1$层的$k$, $v$值就已经保留了!

然后我们把本次新算出来的$k$, $v$值也存储起来。

$$cach{e}_1=\left[(k_0,v_0),(k_1,v_1)\right]$$

$$cach{e}_2=\left[(k_0,v_0),(k_1,v_1),(k_2,v_2)\right]$$

然后我们再做下一次计算出的结果:

$$cach{e}_3=\left[(k_0,v_0),(k_1,v_1),(k_2,v_2),(k_3,v_3)\right]$$

这样就节省了attention和FFN的很多重复计算。

transformers中，生成的时候传入use_cache=True就会开启KV Cache。

也可以简单看下GPT2中的实现，中文注释的部分就是使用缓存结果和更新缓存结果

Class GPT2Attention(nn.Module):
    ...
    ...
    def forward(
        self,
        hidden_states: Optional[Tuple[torch.FloatTensor]],
        layer_past: Optional[Tuple[torch.Tensor]] = None,
        attention_mask: Optional[torch.FloatTensor] = None,
        head_mask: Optional[torch.FloatTensor] = None,
        encoder_hidden_states: Optional[torch.Tensor] = None,
        encoder_attention_mask: Optional[torch.FloatTensor] = None,
        use_cache: Optional[bool] = False,
        output_attentions: Optional[bool] = False,
    ) -> Tuple[Union[torch.Tensor, Tuple[torch.Tensor]], ...]:
        if encoder_hidden_states is not None:
            if not hasattr(self, "q_attn"):
                raise ValueError(
                    "If class is used as cross attention, the weights `q_attn` have to be defined. "
                    "Please make sure to instantiate class with `GPT2Attention(..., is_cross_attention=True)`."
                )

            query = self.q_attn(hidden_states)
            key, value = self.c_attn(encoder_hidden_states).split(self.split_size, dim=2)
            attention_mask = encoder_attention_mask
        else:
            query, key, value = self.c_attn(hidden_states).split(self.split_size, dim=2)

        query = self._split_heads(query, self.num_heads, self.head_dim)
        key = self._split_heads(key, self.num_heads, self.head_dim)
        value = self._split_heads(value, self.num_heads, self.head_dim)

        # 过去所存的值
        if layer_past is not None:
            past_key, past_value = layer_past
            key = torch.cat((past_key, key), dim=-2)  # 把当前新的key加入
            value = torch.cat((past_value, value), dim=-2)  # 把当前新的value加入

        if use_cache is True:
            present = (key, value)  # 输出用于保存
        else:
            present = None

        if self.reorder_and_upcast_attn:
            attn_output, attn_weights = self._upcast_and_reordered_attn(query, key, value, attention_mask, head_mask)
        else:
            attn_output, attn_weights = self._attn(query, key, value, attention_mask, head_mask)

        attn_output = self._merge_heads(attn_output, self.num_heads, self.head_dim)
        attn_output = self.c_proj(attn_output)
        attn_output = self.resid_dropout(attn_output)

        outputs = (attn_output, present)
        if output_attentions:
            outputs += (attn_weights,)

        return outputs  # a, present, (attentions)

总的来说，KV Cache是以空间换时间的做法，通过使用快速的缓存存储，减少了重复计算。（注意，只能在decoder结构的模型可用，因为有mask attention的存在，使得前面的token可以不用关照后面的token）

但是，用了KV Cache之后也不是立刻万事大吉。

我们简单计算一下，对于输入长度为$L$，层数为$L$，hidden size为$d$的模型，需要缓存的参数量为

$$2\times L\times s\times d$$

如果使用的是半精度浮点数，那么每个值所需要的空间就是

$$2\times 2\times L\times s\times d$$

以Llama2 7B为例，有$L=32$，$L=4096$，那么每个token所需的缓存空间就是524,288 bytes，约524k，假设$s=1024$，则需要占用536,870,912 bytes，超过500M的空间。

这些参数的大小是batch size=1的情况，如果batch size增大，这个值是很容易就超过1G。

减小KV cache的方法

业界针对KV Cache的优化，衍生出很多方法，方法主要有四类：

• 共享KV：多个Head共享使用1组KV，将原来每个Head一个KV，变成1组Head一个KV，来压缩KV的存储。代表方法：GQA，MQA等
• 窗口KV：针对长序列控制一个计算KV的窗口，KV cache只保存窗口内的结果（窗口长度远小于序列长度），超出窗口的KV会被丢弃，通过这种方法能减少KV的存储，当然也会损失一定的长文推理效果。代表方法：Longformer等
• 量化压缩：基于量化的方法，通过更低的Bit位来保存KV，将单KV结果进一步压缩，代表方法：INT8等
• 计算优化：通过优化计算过程，减少访存换入换出的次数，让更多计算在片上存储SRAM进行，以提升推理性能，代表方法：flashAttention等

共享KV主要有两种方法，MQA和GQA都是Google提出的

MHA:Multi-Head Attention

论文标题：Attention Is All You Need
论文链接：https://arxiv.org/pdf/1706.03762

MHA在2017年就随着《Attention Is All You Need》一起提出，主要干的就是一个事：把原来一个attention计算，拆成多个小份的attention，并行计算，分别得出结果，最后再合回原来的维度。

假设原来模型的hidden size是$d$，在MHA中，会把投影后的$Q,K,V$在hidden state的维度上切成$hea{d}_{num}$份，每个头的维度是$d_{head}$。这$hea{d}_{num}$组小$Q,K,V$分别独立进行attention计算，之后把得到的$hea{d}_{num}$维度$d_{head}$的输出concat起来。
直接看这个amazing的图，很直观

我们希望多个头能够在训练中学会注意到不同的内容。例如在翻译任务里，一些attention head可以关注语法特征，另一些attention head可以关注单词特性。这样模型就可以从不同角度来分析和理解输入信息，获得更好的效果了。

MQA:Multi-Query Attention

论文标题：Fast Transformer Decoding: One Write-Head is All You Need
论文链接：https://arxiv.org/pdf/1911.02150

MQA就是减少所有所需要的重的。

Google在2019年就提出了《Fast Transformer Decoding: One Write-Head is All You Need》提出了MQA，不过那时候主要是针对的人不多，那是大家主要还是关注在用Bert也开始创新上。

MQA的做法其实很简单。在MHA中，输入分别经过$W_Q,W_K,W_V$的变换之后，都切成$7$份（$n$=头数），维度也从$d_{model}$降到$d_{head}$，分别进行attention计算再拼接。而MQA这一步，在运算过程中，首先对$Q$进行切分（和MHA一样），而$K,V$则直接在在线变换的时候把维度压到$d_{head}$（而不是切分开），然后返回每个Query头分别和一份$K,V$进行attention计算，之后最终结果拼接起来。

简而言之，就是MHA中，每个注意力头的$K,V$是不一样的，而MQA这里，每个注意力头的$K,V$是一样的，值是共享的。而性别效果和MHA一样。

这样来讲，需要缓存的$K,V$值一下就从所有头变成一个头的量。

比如在Llama2 7B中使用的是32个头，那么MQA后，1024个token需要缓存的量就变成$1/32$, 536,870,912 bytes / 32 = 16,777,216 bytes，差不多是16M，这就能明显减少存储了。

（实际上，就是改一下线性变换矩阵，然后把$K,V$的处理划分变成共享，就不用缓存。）

当然，由于共享了多个头的参数，限制了模型的表示能力，MQA虽然能耗费支持推理加速，但是是在最大头数上略有差一点，但是真并不多，且相比其他修改hidden size或head num的做法效果都好。

GQA:Grouped Query Attention

论文标题：GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints
论文链接：https://arxiv.org/pdf/2305.13245

既然MQA对效果有点影响，MHA存储又有不下，那2023年GQA（Grouped-Query Attention）就提出了一个折中的办法，既能减少MQA效果的损失，又相比MHA需要更少的存储。

GQA是，$Q$ 还是按原来MHA/MQA的做法不变。只使用一套共享的$K,V$就能效果不好吗，那就还是多个头。但是要不要太多，数量还是比$Q$的头数少一些，这样相当于把多个头分成group，同一个group内的$K,V$共享，同不group的$Q$所用的$K,V$不同。

MHA可以认为是$K,V$头数最大时的GQA，而MQA可以认为是$K,V$头数少时的GQA。

效果怎么样呢？

看表中2/3/4行对比，GQA的速度相比MHA有明显提升，而效果上比MQA也好一些，能做到和MHA基本没差距。文中提到，这里的MQA和GQA都是通过average pooling从MHA初始化而来，然后进行了少量的训练得到的。如果我们想要把之前用MHA训练的模型改造成GQA，也可以通过这样的方法，增加少量训练来实现。当然如果从一开始就加上，从零开始训练，也是没有问题的。

Llama2用的就是GQA，在tech report中也做了MHA、MQA、GQA的效果对比，可以看到效果确实很不错。

MLA:Multi-head Latent Attention

论文标题：DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model
论文链接：https://arxiv.org/abs/2405.04434

研究动机

随着LLM参数量持续地增加，其在训练和推理过程中面临着巨大的计算资源和低推理效率的挑战。 尽管也出现了Grouped-Query Attention (GQA) 和 Multi-Query Attention (MQA)这类改进Multi-Head Attention (MHA) 以提高推理效率的自注意力机制技术，但模型性能可能会有所降低。

根据论文及博客，DeepSeek-V2在DeepSeek上进行改进，但并没有沿用主流的“类LLaMA的Dense结构”和“类Mistral的Sparse结构”，而是对Transformer架构中的自注意力机制进行了全方位的创新，提出了MLA（Multi-head Latent Attention）结构，并使用了自研的稀疏MoE技术进一步将计算量降低，大幅提高了推理效率。

DeepSeek-V2架构示意图：MLA通过显著减少生成过程中的KV缓存，确保了高效的推理；而DeepSeekMoE则通过稀疏架构，以低成本训练出强大的模型。

模型结构

MLA（Memory-efficient Latent Attention） 的核心思想是将注意力输入 $h_t$ 压缩到一个低维的潜在向量，记作 $c_t^{KV}$，其维度 $d_c$ 远小于原始的 $h_n\cdot d_h$ 维度。这样，在计算注意力时，我们可以通过映射将该潜在向量恢复到高维空间，以重构键（keys）和值（values）。这种方法的优势在于，只需存储低维的潜在向量，从而大幅减少内存占用。

这一过程可以用以下公式描述：

• $c_t^{KV}$ 是低维的潜在向量。
• $W^{DKV}$ 是一个压缩矩阵（down-projection matrix），用于将 $h_t$ 的维度从 $h_n\cdot d_h$ 降维到 $d_c$（其中 D 代表“降维”）。
• $W^{UK}$ 和 $W^{UV}$ 是两个向上投影矩阵（up-projection matrices），分别用于将共享的潜在向量映射回高维空间，以恢复键(K)和值(V)。

类似地，我们也可以将查询（queries）映射到一个低维的潜在向量，并再将其映射回原始的高维空间。这种方法可以降低存储和计算的成本，同时保持注意力机制的有效性。

MLA 的核心思想是通过低秩联合压缩技术，减少 K 和 V 矩阵的存储和计算开销。

MLA从LoRA的成功借鉴经验，实现了比GQA这种通过复制参数压缩矩阵尺度的方法更为节省的低秩推理，同时对模型的效果损耗不大。

为了展示 MLA（Memory-Limited Attention）的完整计算过程，我们提供其详细公式如下：

1. 查询的低秩压缩计算
   $$c_t^Q=W^{DQ}{h}_t$$
   这里，$c_t^Q\in {\mathbb{R}}^{d_c^{\prime }}$ 是查询的压缩潜在向量，用于降低计算复杂度，其中 $d_c^{\prime }\ll d_h{n}_h$ 代表降维后的查询表示。

2. 查询向量计算
   $$[q_{t,1}^C,q_{t,2}^C,...,q_{t,n_h}^C]=q_t^C=W^{UQ}{c}_t^Q$$
   这里 $q_t^C$ 代表查询向量，由 $c_t^Q$ 通过变换矩阵 $W^{UQ}$ 获得。

3. 查询向量位置编码计算
   $$[q_{t,1}^R,q_{t,2}^R,...,q_{t,n_h}^R]=q_t^R=\text{RoPE}(W^{QR}{c}_t^Q)$$
   这里的 $q_t^R$ 代表带有旋转位置编码（RoPE）的查询向量，适用于位置敏感的注意力机制，其中，$W^{QR}\in {\mathbb{R}}^{d_h^R{n}_h\times d_c}$ 是用于生成解耦查询的矩阵。

   我们注意到在增加 RoPE 位置编码并没有在上述计算出的 $q_t^C,k_t^C$ 的基础上乘以 RoPE 的对角矩阵。而是单独计算了两个带着位置编码的 $q_t^R,k_t^R$，如公式 (39) 和公式 (43) 所示。

   为什么这样做呢？因为在MLA的KV压缩机制（KV compression）下，Key（k）和Value（v）在存储时会被压缩，而RoPE的位置变换会影响Key的表示，这导致在计算Query-Key相似度时，RoPE的位置信息可能会引入误差。DeepSeek-V2论文中有一段原文解释（中文翻译）：

   DeepSeek-67B计划在 DeepSeek-V2 中使用旋转位置嵌入（RoPE）。然而，RoPE 与低秩 KV 压缩不兼容。具体来说，RoPE 对查询（query）和键（key）均具有位置敏感性。如果对键 $K^c,W^K$ 应用 RoPE，则 $W^K$ 会与一个位置敏感的 RoPE 矩阵耦合。在推理过程中，$W^K$ 无法像 $W^Q$ 那样进行吸收，因为 RoPE 矩阵与当前生成的 token 相关，且 $W^Q$ 与 $W^K$ 之间的矩阵乘法不符合交换律。因此，在推理时，必须为所有前缀 token 重新计算键，这会显著降低推理效率。

   为了解决这一问题，提出了解耦 RoPE（Decoupled RoPE）策略，该策略使用额外的多头查询 $q_i^R\in {\mathbb{R}}^{d^R}$ 和一个共享的键 $k_i^R\in {\mathbb{R}}^{d^R}$ 来携带 RoPE，其中 $d^R$ 代表解耦后的查询和键的每头维度。采用解耦 RoPE 策略后，多头注意力（MLA）的计算如下：

$$[q_t^R,q_1^R,q_2^R,...,q_n^R]=q^R=\text{RoPE}(W^{QR}{c}_t)\text{\hspace{1em}(14)}$$

$$k_t^R=\text{RoPE}(W^{KR}{h}_t)\text{\hspace{1em}(15)}$$

$$q_{t,i}=[q_i^c,q_i^R]\text{\hspace{1em}(16)}$$

$$k_{t,i}=[k_i^c,k_i^R]\text{\hspace{1em}(17)}$$

$$o_{t,i}=\sum _{j=1}^n{\text{Softmax}}_j\left(\frac{q_{t,i}^T{k}_{j,i}}{\sqrt{d_h+d_h^R}}\right)v_{j,i}\text{\hspace{1em}(18)}$$

$$u_t=w^T[o_{t,1},o_{t,2},...,o_{t,n}]\text{\hspace{1em}(19)}$$

其中 $W^{QR}\in {\mathbb{R}}^{d_h^R\times d}$ 和 $W^{KR}\in {\mathbb{R}}^{d_h^R\times d}$ 为解耦查询和键的投影矩阵，$\text{RoPE}(\cdot )$ 表示 RoPE 变换操作，$[\cdot ;\cdot ]$ 表示向量拼接操作。在推理过程中，解耦后的键应被缓存。因此，DeepSeek-V2 需要一个包含 $(d_c+d_h^R)$ 维度的 KV 缓存。

更多细节可以参考这篇文章，非常细！deepseek技术解读(1)-彻底理解MLA（Multi-Head Latent Attention）

4. 最终查询向量
   $$q_{t,i}=[q_{t,i}^C,q_{t,i}^R]$$
   这里 $q_{t,i}$ 由 $q_{t,i}^C$ 和 $q_{t,i}^R$ 组成，分别表示标准查询和旋转查询。

5. 键值缓存计算
   $$c_t^{KV}=W^{DKV}{h}_t$$
   这里 $c_t^{KV}$ 是通过矩阵 $W^{DKV}$ 计算得到的键值内容，（蓝框部分代表需要缓存的向量）。

6. 键值计算
   $$[k_{t,1}^C,k_{t,2}^C,...,k_{t,n_h}^C]=k_t^C=W^{UK}{c}_t^{KV}$$
   $$k_t^R=\text{RoPE}(W^{KR}{h}_t)$$
   $$k_{t,i}=[k_{t,i}^C,k_{t,i}^R]$$
   这里的键向量 $k_t^C$ 和 $k_t^R$ 通过不同方式计算，并合并为最终键向量 $k_{t,i}$。

7. 值向量计算
   $$[v_{t,1}^C,v_{t,2}^C,...,v_{t,n_h}^C]=v_t^C=W^{UV}{c}_t^{KV}$$
   这里 $v_t^C$ 代表值向量，同样需要缓存以加速计算。

8. 注意力计算
   到目前为止，我们得到的$q,k$包括两部分拼接而成：一部分是做了低秩压缩得到的$q,k$向量，一部分是增加了RoPE位置编码的$q,k$向量,分别是公式(40)和公式(44)。

   $$o_{t,i}=\sum _{j=1}^t{\text{Softmax}}_j\left(\frac{q_{t,i}^T{k}_{j,i}}{\sqrt{d_h}+d_h^R}\right)v_{j,i}^C$$
   这里采用标准的注意力计算方法，即查询和键点积后归一化，再加权值向量。

9. 最终输出计算
   $$u_t=W^O[o_{t,1},o_{t,2},...,o_{t,n_h}]$$
   最终输出 $u_t$ 通过权重矩阵 $W^O$ 变换得到。

   在推理阶段，为了避免重复计算，我们可以缓存 $c_t^{KV}$ 并从中恢复 $k_t^C$ 和 $v_t^C$，从而降低计算开销。这是通过矩阵变换的结合（如将 $W^{UK}$ 吸收进 $W^{UQ}$）来优化的。这样，我们可以避免对每个查询重新计算键和值，从而提升推理效率。

模型效果

如DeepSeek-V2架构示意图右下所示，大模型使用kv-cache进行模型的解码加速，但是当序列较长的情况下很容易出现显存不足的问题，MLA从这一角度出发，致力于减少kv缓存的占用。

多头注意力（MHA）、分组查询注意力（GQA）、多查询注意力（MQA）和多头潜在注意力（MLA）的简化示意图。通过将键（keys）和值（values）联合压缩到一个潜在向量中，MLA在推理过程中显著减少了KV缓存的大小。

从上图我们可以看到，虽然MLA缓存的Latent KV比较短（相当于2.25个MQA的缓存量），但MLA有恢复全 k,v 的能力，特征表达能力显著比GQA、MQA要强。所以MLA能做到又快又省又强。论文中也给出了下图的数据

NSA:Native Sparse Attention

Native Sparse Attention: Hardware-Aligned and Natively Trainable Sparse Attention

论文地址：https://arxiv.org/abs/2502.11089

研究背景与动机

在自然语言处理领域，长上下文建模对下一代大语言模型至关重要，其应用场景广泛，如深度推理、代码生成、多轮对话等。然而，标准注意力机制计算复杂度高，当处理长序列时，计算成本剧增，成为模型发展的瓶颈。以解码64k长度上下文为例，softmax注意力计算的延迟占总延迟的70 - 80%，这凸显了寻求高效注意力机制的紧迫性。

为提升效率，利用softmax注意力的固有稀疏性是一种可行途径，即选择性计算关键查询 - 键对，在保持性能的同时降低计算开销。现有方法虽各有探索，但在实际应用中存在诸多局限：

1. 推理效率假象：许多稀疏注意力方法在推理时未能实现预期的加速效果。一方面，部分方法存在阶段受限的稀疏性，如H2O在解码阶段应用稀疏性，但预填充阶段计算量大；MInference则只关注预填充阶段稀疏性，导致至少一个阶段计算成本与全注意力相当，无法在不同推理负载下有效加速。另一方面，一些方法与先进注意力架构不兼容，如Quest在基于GQA的模型中，虽能减少计算操作，但KV缓存内存访问量仍较高，无法充分利用先进架构的优势。
2. 可训练稀疏性的误区：仅在推理阶段应用稀疏性会导致模型性能下降，且现有稀疏注意力方法大多未有效解决训练阶段的计算挑战。例如，基于聚类的方法（如ClusterKV）存在动态聚类计算开销大、算子优化困难、实现受限等问题；一些方法的离散操作（如MagicPIG中的SimHash选择）使计算图不连续，阻碍梯度传播；HashAttention等方法的非连续内存访问模式，无法有效利用快速注意力技术（如FlashAttention），降低了训练效率。

针对这些问题，本文提出了原生可训练的稀疏注意力机制（Native Sparse Attention，NSA），旨在通过算法创新与硬件对齐优化，实现高效的长上下文建模，平衡模型性能与计算效率。

NSA核心工作

NSA的技术方法涵盖算法设计与内核优化。其整体框架基于对注意力机制的重新定义，通过设计不同的映射策略构建更紧凑、信息更密集的键值对表示，以减少计算量。同时，针对硬件特性进行内核优化，提升实际运行效率。

1. 背景知识
   • 注意力机制：在语言建模中，注意力机制广泛应用。对于输入序列长度为$t$的情况，注意力操作定义为：
     $$o_t=Attn\left(q_t,k_{:t},v_{:t}\right)$$
     其中$Attn$表示注意力函数：
     $$Attn\left(q_t,k_{:t},v_{:t}\right)=\sum _{i=1}^t\frac{{\alpha }_{t,i}{v}_i}{{\sum }_{j=1}^t{\alpha }_{t,j}},{\alpha }_{t,i}=e^{\frac{q_t^{\top }{k}_i}{\sqrt{d_k}}}$$
     这里${\alpha }_{t,i}$是$q$与$k_i$之间的注意力权重，$d_k$是键的特征维度。随着序列长度增加，注意力计算在总计算成本中占比越来越大，给长上下文处理带来挑战。
   • 算术强度：算术强度是计算操作与内存访问的比率，对硬件上的算法优化有重要影响。每个GPU都有由峰值计算能力和内存带宽决定的临界算术强度。对于计算任务，算术强度高于此临界阈值时受GPU浮点运算能力（FLOPS）限制，低于此阈值时受内存带宽限制。在因果自注意力机制中，训练和预填充阶段，批矩阵乘法和注意力计算算术强度高，属于计算受限阶段；而自回归解码时，每次前向传递仅生成一个令牌，但需加载整个键值缓存，算术强度低，受内存带宽限制。这导致不同阶段的优化目标不同：训练和预填充阶段需降低计算成本，解码阶段需减少内存访问。
2. 整体框架：为利用注意力的自然稀疏模式，NSA提出用更紧凑的键值对${\tilde{K}}_t$、${\tilde{V}}_t$替代原始键值对$k_{:t}$、$v_{:t}$ 。优化后的注意力输出定义为：
   $${\tilde{K}}_t=f_K\left(q_t,k_{:t},v_{:t}\right),{\tilde{V}}_t=f_V\left(q_t,k_{:t},v_{:t}\right)$$
   $$o_t^{\ast }=Attn\left(q_t,{\tilde{K}}_t,{\tilde{V}}_t\right)$$
   其中${\tilde{K}}_t$、${\tilde{V}}_t$根据当前查询$q_t$和上下文内存$k_{:t}$、$v_{:t}$动态构建。通过设计多种映射策略可得到不同类别的${\tilde{K}}_t^c$、${\tilde{V}}_t^c$ ，并将它们组合起来：
   $$o_t^{\ast }=\sum _{c\in C}{g}_t^c\cdot Attn\left(q_t,{\tilde{K}}_t^c,{\tilde{V}}_t^c\right)$$
   NSA有三种映射策略 C = { c m p , s l c , w i n } C = \{cmp, slc, win\} C={cmp,slc,win}，分别代表压缩、选择和滑动窗口策略，用于处理键值对。$g_t^c\in [0,1]$是对应策略$c$的门控分数，由输入特征经MLP和sigmoid激活得到。令$N_t$表示重新映射后的键/值总数：
   $$N_t=\sum _{c\in C}size[{\tilde{K}}_t^c]$$
   通过确保$N_t\ll t$，NSA保持较高的稀疏率。
3. 算法设计
   • 令牌压缩（Token Compression）：通过聚合连续的键或值块为块级表示，得到压缩后的键值对，以捕获整个块的信息。压缩键表示定义为：
     $${\tilde{K}}_t^{cmp}=f_K^{cmp}\left(k_{:t}\right)=\left\{\phi \left(k_{id+1:id+l}\right)|1\le i\le \lfloor \frac{t-l}{d}\rfloor \right\}$$
     其中$l$是块长度，$d$是相邻块之间的滑动步长，$\phi$是带有块内位置编码的可学习MLP，用于将块中的键映射为单个压缩键。${\tilde{K}}_t^{cmp}\in {\mathbb{R}}^{d_k\times \lfloor \frac{t-l}{d}\rfloor }$是由压缩键组成的张量。通常采用$d<l$来减少信息碎片化。类似地，可定义压缩值表示${\tilde{V}}_t^{cmp}$。压缩表示捕获更粗粒度的高级语义信息，降低注意力计算负担。
   • 令牌选择（Token Selection）：仅使用压缩键值对可能会丢失重要的细粒度信息，因此NSA设计了高效的令牌选择机制。
     • 块级选择（Blockwise Selection）：基于硬件效率和注意力分数的固有分布模式，NSA的选择策略按空间连续块处理键值序列。现代GPU架构对连续块访问具有更高的吞吐量，且块级计算能更好地利用张量核心。此外，注意力分数通常具有空间连续性，相邻键往往具有相似的重要性水平。
     • 重要性分数计算（Importance Score Computation）：计算块重要性分数可能会带来较大开销。NSA利用压缩令牌的注意力计算产生的中间注意力分数来推导选择块的重要性分数。公式为：
       $$p_t^{cmp}=Softmax\left(q_t^T{\tilde{K}}_t^{cmp}\right)$$
       其中$p_t^{cmp}\in {\mathbb{R}}^{\lfloor \frac{t-l}{d}\rfloor }$是$q_t$与压缩键${\tilde{K}}_t^{cmp}$之间的注意力分数。当压缩块和选择块具有相同的分块方案（即$l^{\prime }=l=d$）时，可直接得到选择块重要性分数$p_t^{slc}=p_t^{cmp}$。对于分块方案不同的情况（假设$d|l$且$d|l^{\prime }$），通过下式推导选择块的重要性分数：
       $$p_t^{slc}[j]=\sum _{m=0}^{\frac{l^{\prime }}{d}-1}\sum _{n=0}^{\frac{l}{d}-1}{p}_t^{cmp}\left[\frac{l^{\prime }}{d}j+m+n\right]$$
       在采用GQA或MQA的模型中，为最小化解码时的KV缓存加载，需确保跨查询头的一致块选择。同一组内跨头的共享重要性分数定义为：
       $$p_t^{sl{c}^{\prime }}=\sum _{h=1}^H{p}_t^{slc,(h)}$$
       其中$h$表示头索引，$H$是每组中的查询头数量。
     • Top - n块选择（Top - n Block Selection）：获得选择块重要性分数后，保留按块重要性分数排名前$n$的稀疏块中的令牌。公式为：
       $$I_t=\left\{i|rank\left(p_t^{sl{c}^{\prime }}[i]\right)\le n\right\}$$
       $${\tilde{K}}_t^{slc}=Cat\left[\left\{k_{i{l}^{\prime }+1:(i+1)l^{\prime }}|i\in I_t\right\}\right]$$
       其中$rank(\cdot )$表示降序排名位置，$rank=1$对应最高分数，$I_t$是所选块的索引集，$Cat$表示拼接操作。${\tilde{K}}_t^{slc}\in {\mathbb{R}}^{d_k\times n{l}^{\prime }}$是由选择的键组成的张量。类似地，可定义细粒度值${\tilde{V}}_t^{slc}$。这些选择的键值对参与与$q_t$的注意力计算。
   • 滑动窗口（Sliding Window）：在注意力机制中，局部模式可能会主导学习过程，影响模型从压缩和选择令牌中学习。为解决此问题，NSA引入滑动窗口分支专门处理局部上下文。具体而言，NSA维护一个窗口$w$内的近期令牌${\tilde{K}}_t^{win}=k_{t-w:t}$，${\tilde{V}}_t^{win}=v_{t-w:t}$ ，并将不同信息源（压缩令牌、选择令牌、滑动窗口）的注意力计算分离到不同分支。这些分支输出通过学习的门控机制聚合。为防止注意力分支间的梯度干扰，NSA为三个分支提供独立的键值对。这种架构设计在引入最小开销的同时，通过防止局部和长距离模式识别之间的梯度干扰，实现稳定学习。
   • 最终输出计算：获得压缩、选择和滑动窗口这三类键值对（${\tilde{K}}_t^{cmp}$，${\tilde{V}}_t^{cmp}$；${\tilde{K}}_t^{slc}$，${\tilde{V}}_t^{slc}$；${\tilde{K}}_t^{win}$，${\tilde{V}}_t^{win}$）后，按照公式$o_t^{\ast }={\sum }_{c\in C}{g}_t^c\cdot Attn\left(q_t,{\tilde{K}}_t^c,{\tilde{V}}_t^c\right)$计算最终的注意力输出，这构成了NSA完整的算法框架。
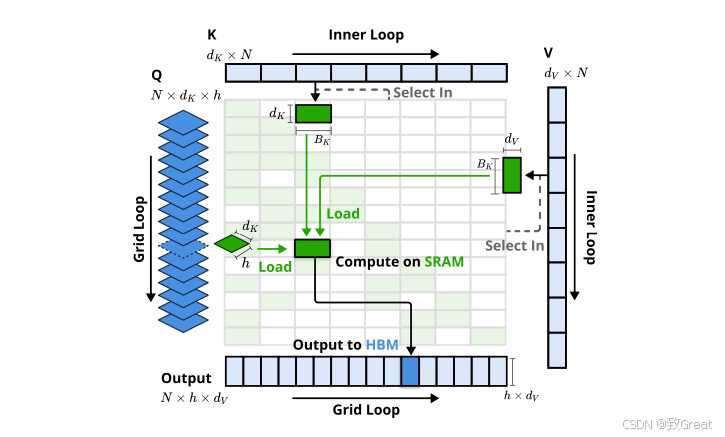
4. 内核设计：为在训练和预填充阶段实现类似FlashAttention的加速效果，NSA基于Triton实现了硬件对齐的稀疏注意力内核。当前先进的大语言模型多采用共享KV缓存的架构（如GQA和MQA），NSA聚焦于此。压缩和滑动窗口注意力计算可与现有FlashAttention - 2内核兼容，而对于稀疏选择注意力，NSA提出了专门的内核设计。若采用FlashAttention将时间连续的查询块加载到SRAM的策略，由于块内查询可能需要不连续的KV块，会导致内存访问效率低下。NSA的关键优化在于采用不同的查询分组策略：对于查询序列上的每个位置，将GQA组内的所有查询头（它们共享相同的稀疏KV块）加载到SRAM。其内核设计具有以下关键特征：
   • 以组为中心的数据加载（Group - Centric Data Loading）：对于每个内循环，加载组内位置$t$处所有头的查询$Q\in {\mathbb{R}}^{[h,d_k]}$及其共享的稀疏键/值块索引$I_t$。
   • 共享KV获取（Shared KV Fetching）：在内循环中，按$I_t$顺序将连续的键/值块加载到SRAM中，分别表示为$K\in {\mathbb{R}}^{[B_k,d_k]}$，$V\in {\mathbb{R}}^{[B_k,d_v]}$，以最小化内存加载，其中$B_k$是满足$B_k|l^{\prime }$的内核块大小。
   • 网格外循环（Outer Loop on Grid）：由于不同查询块的内循环长度（与所选块数$n$成比例）几乎相同，NSA将查询/输出循环放入Triton的网格调度器中，简化并优化内核。
   • 优势：这种设计通过组间共享消除冗余的KV传输，并平衡GPU流式多处理器的计算负载，实现接近最优的算术强度。

性能评估

1. 预训练设置：模型采用270亿参数的骨干结构，结合GQA和MoE进行训练，使用YaRN在32K长度文本上继续训练以适应长上下文。NSA在预训练损失上优于全注意力模型。
2. 基线方法：除与全注意力模型对比外，还评估了H2O、infLLM、Quest等稀疏注意力方法，长上下文评估中对所有基线方法进行比较。
3. 性能比较
   • 一般评估：NSA在9个基准中超越7个，包括推理任务（DROP、GSM8K等），显示出其稀疏注意力在减少噪声、聚焦重要信息上的优势。
   • 长上下文评估：NSA在64k上下文的“Needle-in-a-Haystack”测试中表现完美，且在LongBench上超越了所有基线模型，提升了多跳问答和代码理解任务的性能。
   • 思维链推理评估：NSA在知识蒸馏的数学推理任务（AIME 24基准）中，比全注意力模型在8k和16k上下文下分别提高0.075和0.054，验证了其长距离逻辑依赖的捕捉能力。
4. 效率分析
   • 训练速度：在64k上下文下，NSA的前向传播速度提升9倍，反向传播速度提升6倍，得益于硬件对齐设计。
   • 解码速度：NSA在64k上下文下的解码速度提升11.6倍，显著降低了解码延迟，尤其随着序列长度增加。
     

MoBA: Mixture of Block Attention for Long-Context LLMs

论文标题：Mixture of Block Attention for Long-Context LLMs
论文地址：https://github.com/MoonshotAI/MoBA/blob/master/MoBA_Tech_Report.pdf

扩展大语言模型（LLMs）的有效上下文长度对迈向通用人工智能（AGI）意义重大，但传统注意力机制的二次计算复杂度带来高昂开销。现有方法存在局限，如基于预定义结构的方法缺乏通用性，线性近似方法在复杂推理任务中的效果有待探究。本文提出混合块注意力（MoBA）机制，遵循“少结构”原则，将专家混合（MoE）原理应用于注意力机制。MoBA在长上下文任务中表现卓越，能在全注意力和稀疏注意力间无缝切换，提升效率的同时不降低性能。

该机制已应用于支持Kimi的长上下文请求，为LLMs的高效注意力计算带来显著进展，代码可在https://github.com/MoonshotAI/moba获取。

研究动机

LLMs发展与长上下文处理需求

追求通用人工智能推动大语言模型向大规模发展，处理长序列的能力成为关键，它在历史数据分析、复杂推理决策等众多应用中至关重要。从Kimi、Claude、Gemini等模型对长输入提示的理解，以及Kimi k1.5、DeepSeek - R1、OpenAI o1/o3对长思维链输出能力的探索，都能看出对扩展上下文处理能力的迫切需求。

长序列处理面临的挑战

由于传统注意力机制（Waswani等人，2017）计算复杂度随序列长度呈二次增长，扩展LLMs的序列长度并非易事。为解决这一问题，研究主要集中在利用注意力分数的稀疏性来提高效率，同时不牺牲性能。

现有方法的局限

• 基于预定义结构的方法：像基于汇聚（sink - based）（G. Xiao等人，2023）或滑动窗口注意力（Beltagy等人，2020）这类方法，通过预定义结构利用稀疏性，但高度依赖特定任务，可能限制模型的通用性。
• 动态稀疏注意力机制：Quest（Tang等人，2024）、Minference（H. Jiang等人，2024）和RetrievalAttention（Di Liu等人，2024）等动态稀疏注意力机制，在推理时选择部分令牌，虽能减少长序列计算量，但无法大幅降低长上下文模型的训练成本，难以高效扩展到数百万令牌的上下文。
• 线性注意力模型：Mamba（Dao和Gu，2024）、RWKV（Peng、Alcaide等人，2023；Peng、Goldstein等人，2024）和RetNet（Sun等人，2023）等线性注意力模型，用线性近似替代传统的基于softmax的注意力，降低长序列处理的计算开销。然而，线性和传统注意力差异大，适配现有Transformer模型成本高，或需从头训练新模型，且在复杂推理任务中的有效性证据有限。

在这样的背景下，本文提出MoBA。它基于MoE原理，应用于Transformer模型的注意力机制，通过将上下文划分为块，并采用门控机制选择性地将查询令牌路由到最相关的块，提高LLMs效率，使模型能处理更长更复杂的提示，同时降低资源消耗。

研究方法

预备知识：Transformer中的标准注意力

Transformer中的标准注意力计算如下：对于单个查询令牌$q\in {\mathbb{R}}^{1\times d}$，它关注$N$个键和值令牌，分别表示为$K,V\in {\mathbb{R}}^{N\times d}$，标准注意力计算为$$\text{Attn}(q,K,V)=\text{Softmax}(q{K}^{\top })V$$，其中$d$表示单个注意力头的维度。为简化说明，这里聚焦单头注意力场景，多头注意力则是将多个单头注意力操作的输出连接起来。

MoBA架构

• 块分区和选择策略：与标准注意力不同，MoBA使每个查询令牌仅关注部分键和值，公式为$$\text{MoBA}(q,K,V)=\text{Softmax}(qK[I{]}^{\top })V[I]$$，其中$I\subseteq [N]$是选定的键和值的集合。MoBA的关键创新在于块分区和选择策略。将长度为$N$的完整上下文划分为$n$个块，每个块代表后续令牌的一个子集，假设上下文长度$N$能被块数$n$整除，记$B=\frac{N}{n}$为块大小，第$i$个块的范围为$I_i=[(i-1)\times B+1,i\times B]$ 。通过应用MoE中的top - k门控机制，模型能让每个查询选择性地关注不同块中的部分令牌，而非整个上下文，即$I={\bigcup }_{g_i>0}{I}_i$ 。
• 门控机制：模型采用门控机制，计算查询$q$与第$i$个块的亲和分数$s_i$，并在所有块中应用top - k门控。第$i$个块的门值$g_i$计算为：
  g i = { 1 s i ∈ Topk ( { s j ∣ j ∈ [ n ] } , k ) 0 otherwise g_{i}= \begin{cases}1 & s_{i} \in \text{Topk}(\{s_{j} | j \in[n]\}, k) \\ 0 & \text{otherwise} \end{cases} gi​={10​si​∈Topk({sj​∣j∈[n]},k)otherwise​
  其中$\text{Topk}(\cdot ,k)$表示包含$k$个最高亲和分数的集合。在本文中，分数$s_i$通过$q$与$K[I_i]$沿序列维度的平均池化的内积计算，即
  $$s_i=⟨q,\text{mean\_pool}(K[I_i])⟩$$
• 运行示例：图1a展示了MoBA的运行示例，有两个查询令牌和四个KV块。路由器（门控网络）为每个查询动态选择前两个块进行关注，第一个查询被分配到第一和第二个块，第二个查询被分配到第三和第四个块。
• 因果性保持：在自回归语言模型中，保持因果性至关重要。MoBA通过两种设计确保因果性：
  • 不关注未来块：MoBA确保查询令牌不会被路由到任何未来块，将注意力范围限制在当前和过去块，遵循语言建模的自回归性质。形式上，记$pos(q)$为查询$q$的位置索引，对于任何满足$pos(q)<i\times B$的块$i$，设置$s_i=-\infty$，$g_i=0$。
  • 当前块注意力和因果掩码：定义“当前块”为包含查询令牌本身的块。为避免当前块注意力计算中因平均池化包含未来令牌信息而违反因果性，模型强制每个令牌路由到其当前块，并在当前块注意力计算时应用因果掩码。这不仅避免了信息泄露，还鼓励关注局部上下文。形式上，对于查询令牌位置$pos(q)$在区间$I_{\bar{u}}$内的块$i$，设置$g_i=1$。从MoE角度看，MoBA中的当前块注意力类似于现代MoE架构中的共享专家角色。
• 其他关键设计选择：
  • 细粒度块分割：受MoE文献中细粒度专家分割提升模型性能的启发，MoBA沿上下文长度维度进行分割。通过实验发现，块粒度对MoBA性能影响显著，细粒度分割有助于提升模型性能。
  • MoBA与全注意力的混合：MoBA设计为可替代全注意力，且参数数量不变。在初始化阶段，每个注意力层可选择全注意力或MoBA，训练时也可动态切换。实验表明，这种混合策略在平衡训练效率和模型性能方面效果显著。
  • 与滑动窗口注意力和注意力汇聚的比较：滑动窗口注意力和注意力汇聚可视为MoBA的特殊情况。滑动窗口注意力可解释为MoBA的一种变体，其门控网络总是选择最近的块；注意力汇聚可看作MoBA的变体，门控网络总是选择初始块和最近块。这表明MoBA具有更强的表达能力，能灵活近似多种静态稀疏注意力架构。

结构实现

MoBA的高性能实现结合了FlashAttention（Dao、D. Fu等人，2022）和MoE（Rajbhandari等人，2022）的优化技术，主要包含以下五个步骤：

1. 根据门控网络和因果掩码确定查询令牌到KV块的分配。
2. 根据分配的KV块对查询令牌进行排序。
3. 为每个KV块和分配到它的查询令牌计算注意力输出，此步骤可通过可变长度的FlashAttention进行优化。
4. 将注意力输出重新排列回原始顺序。
5. 使用在线Softmax（即平铺）组合相应的注意力输出，因为一个查询令牌可能关注其当前块和多个历史KV块。

算法1详细描述了MoBA的实现流程，首先将KV矩阵划分为块（第1 - 2行），然后计算门控分数（第3 - 7行），应用top - k操作得到查询到KV块的映射矩阵$G$（第8行），接着根据映射排列查询令牌并计算块级注意力输出（第9 - 12行），最后重新排列并组合注意力输出（第16行）。

模型性能

缩放定律实验和消融研究

• LM损失的可扩展性：MoBA与全注意力模型在不同大小的语言模型上验证损失曲线相似，证明MoBA具有与全注意力相当的缩放性能。
• 长上下文可扩展性：尽管MoBA在32K序列长度下的损失略高于全注意力，差距逐渐缩小，表明MoBA适应长上下文任务。
• 细粒度块分割的消融研究：块粒度对MoBA性能影响显著，细粒度分割有助于提升性能，性能差异可达1e-2。

MoBA与全注意力的混合

• MoBA/全注意力混合训练：MoBA/全注意力混合训练平衡了训练效率与模型性能，验证损失与全注意力训练接近，未出现显著损失峰值。
• 层混合策略：在监督微调中，通过将最后几层从MoBA切换到全注意力，显著降低了SFT损失。

大语言模型评估

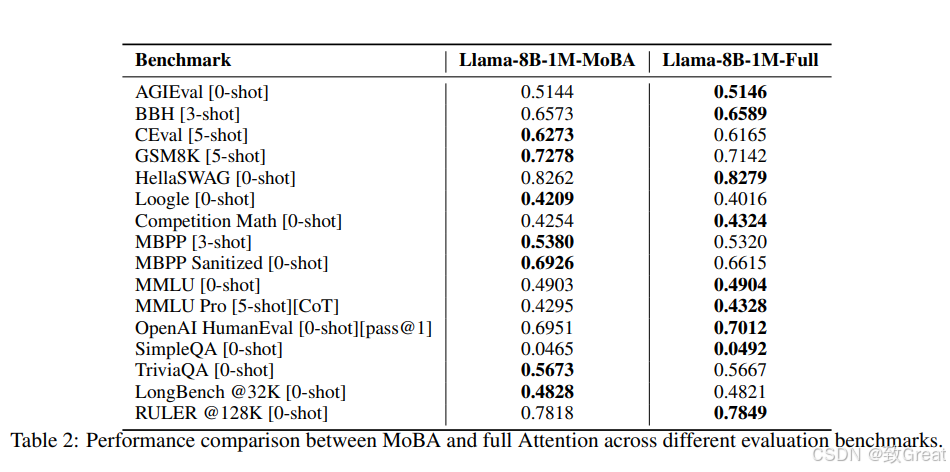
• Llama 3.1 8B基础模型：MoBA与全注意力在多个长上下文基准测试中表现相近，且MoBA在长上下文任务中有较好表现，尤其在RULER和Needle in a Haystack基准测试中，表现几乎相同。
  

效率和可扩展性

• 效率提升：MoBA在所有上下文长度下的前向传播时间较全注意力更高效，计算复杂度为次二次，速度提高可达6.5倍。
• 长度可扩展性：MoBA处理长序列时比全注意力更高效，在处理1000万令牌时计算时间减少16倍。

参考资料

• 缓存与效果的极限拉扯：从MHA、MQA、GQA到MLA
• 【手撕NSA】DeepSeek新作-原生稀疏注意力-超长文(附代码)
• 撞车DeepSeek NSA，Kimi杨植麟署名的新注意力架构MoBA发布，代码也公开
• Deepseek-V2技术报告解读！全网最细！
• 浅读 DeepSeek-V2 技术报告
• 还在用MHA？MLA来了DeepSeek-v2的MLA的总结和思考
• Multi-Head Latent Attention (MLA) 详细介绍（来自Deepseek V3的回答）
• 大模型推理框架 RTP-LLM 架构解析
• DeepSeek-V2 高性能推理 (1)：通过矩阵吸收十倍提速 MLA 算子
• 注意力MHA、MQA、GQA、Linear Attention到MLA
• 大模型KV Cache节省神器MLA学习笔记（包含推理时的矩阵吸收分析）
• MHA、MQA、GQA区别和联系
• MHA vs MQA vs GQA vs MLA