python 实现KPCA核主成分分析

之前写过一篇 《统计学习方法》之主成分分析PCA结合python实现的文章，从算法理论推导和python代码介绍了PCA如何实现，近期遇到了他的高阶版——KPCA（核主成分分析），记录学习一下。

理论知识

核心原理

PCA的核心原理详细推导过程可以参考看《统计学习方法》之主成分分析PCA结合python实现，PCA的核心在于通过线性变换寻找数据分布的主轴。但PCA是一种线性方法，如果数据在原空间中的分布是非线性的，PCA的效果就不理想。核PCA通过核技巧（Kernel Trick）来解决这个问题，它将数据映射到高维空间，在高维空间中找到数据的线性结构，从而捕获原始数据的非线性结构。

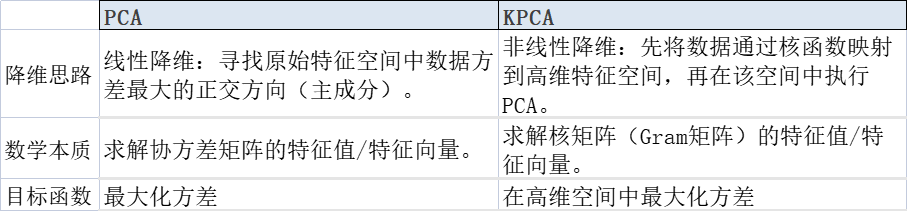
关键区别

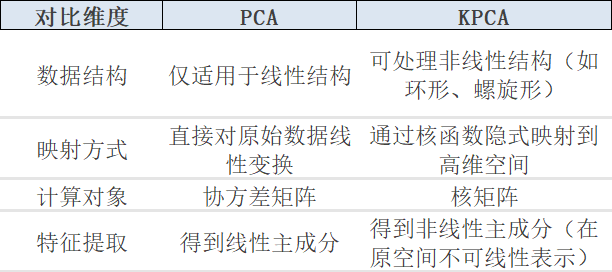
优劣势对比

python实现KPCA

sklearn中 KernelPCA 参数讲解

from sklearn.decomposition import KernelPCA# 创建带有推荐参数的KPCA模型
kpca = KernelPCA(n_components=0.95,      # 保留95%方差kernel='rbf',            # 使用RBF核gamma=0.1,               # RBF核参数eigen_solver='dense',    # 确保可获取特征值fit_inverse_transform=False,  # 不学习逆变换（除非需要重构）remove_zero_eig=True,    # 移除零特征值成分random_state=42          # 可重现结果
)

1. n_components (默认值: None)
含义: 要保留的主成分数量
说明:如果是整数，表示要保留的主成分数量
如果是 None，则保留所有非零特征值对应的成分
如果是浮点数 (0-1之间)，表示保留解释方差的累计比例

2. kernel (默认值: ‘linear’)
含义: 核函数类型
可选值:
‘linear’: 线性核 $K(x,y)=x^{T}y$
‘poly’: 多项式核 $K(x,y)=(\gamma x^{T}y+coef0{)}^d$
‘rbf’: 高斯径向基核 $K(x,y)=\exp (-\gamma |x-y{|}^2)$
‘sigmoid’: Sigmoid核 $K(x,y)=\tanh (\gamma x^{T}y+coef0)$
‘cosine’: 余弦相似度核 $K(x,y)=\frac{x^{T}y}{|x||y|}$
建议: 非线性数据首选 ‘rbf’

3. gamma (默认值: None)
含义: 核函数系数（用于 ‘rbf’, ‘poly’, ‘sigmoid’）
说明:如果为 None，则取 1/(n_features * X.var())
对于 RBF 核，γ 控制高斯函数的宽度
建议:值越大，模型越复杂（过拟合风险）
值越小，模型越简单（欠拟合风险）
常用范围: [0.001, 0.01, 0.1, 1, 10]

4. degree (默认值: 3)
含义: 多项式核的阶数（仅当 kernel=‘poly’ 时有效）
建议: 通常取值 2-5

5. coef0 (默认值: 1)
含义: 核函数中的独立项（用于 ‘poly’ 和 ‘sigmoid’）
说明: 控制多项式核中高阶项与低阶项之间的平衡

6. eigen_solver (默认值: ‘auto’)
含义: 特征值求解器
可选值:
‘auto’: 自动选择
‘dense’: 使用 LAPACK 的密集求解器
‘arpack’: 使用 ARPACK 的迭代求解器
建议:需要特征值（计算方差）时选 ‘dense’
大样本时选 ‘arpack’ 节省内存

7. tol (默认值: 0)
含义: ARPACK 求解器的收敛容差（仅当 eigen_solver=‘arpack’）
说明: 值越小，精度越高，但计算时间越长

8. max_iter (默认值: None)
含义: ARPACK 求解器的最大迭代次数
说明: None 表示使用默认值（通常为 n_components * 20）

9. alpha (默认值: 1.0)
含义: 逆变换的正则化参数（仅当 fit_inverse_transform=True）
说明: 控制逆变换的岭回归正则化强度

10. fit_inverse_transform (默认值: False)
含义: 是否学习逆变换
说明:如果 True，将学习从特征空间回原始空间的映射
用于数据重构和去噪
代价: 增加计算量

11. n_jobs (默认值: None)
含义: 并行计算使用的CPU核心数
说明: None 表示1，-1 表示使用所有核心

sklearn中 KernelPCA 实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import KernelPCA
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler  
plt.rcParams['font.sans-serif'] = ['SimHei']#解决图表中中文显示问题
plt.rcParams['axes.unicode_minus']=False# 解决图表中负号不显示问题
import warnings
warnings.filterwarnings("ignore")
# 设置Seaborn风格
sns.set(style="whitegrid", palette="muted", font_scale=1.2)X = data.data  # 特征矩阵
y = data.target  # 标签
scaler = StandardScaler() 
X_scaled = scaler.fit_transform(X)
# 使用RBF核进行KPCA
# 创建KPCA模型（必须使用 dense 求解器）
kpca = KernelPCA(n_components=3, kernel='rbf', gamma=0.01,eigen_solver='dense'  # 关键：必须用dense求解器才能获取特征值
)# 拟合模型
X_kpca = kpca.fit_transform(X)# 1. 获取特征值 
eigenvalues =  kpca.eigenvalues_ 
print(f'\n特征值: ',eigenvalues)
# 2. 计算方差贡献（特征值归一化）
explained_variance_ratio = eigenvalues / np.sum(eigenvalues)print(f'\nKPCA各个特征的可解释性方差: ',explained_variance_ratio)
print(f'PC1解释的方差比例: {explained_variance_ratio[0]:.4f}')
print(f'PC2解释的方差比例: {explained_variance_ratio[1]:.4f}')
print(f'PC3解释的方差比例: {explained_variance_ratio[2]:.4f}')# 3. 计算累计方差
cumulative_variance = np.cumsum(explained_variance_ratio)
print("KPCA 累计解释方差:", cumulative_variance)# 可视化
plt.figure(figsize=(10, 6))
plt.scatter(X_kpca[:, 2], X_kpca[:, 1], cmap=plt.cm.Spectral, s=20)
plt.title('Kernel PCA on load_iris Data', fontsize=16)
plt.ylabel('Principal Component 2', fontsize=14)
plt.colorbar()
plt.grid(True)
plt.show()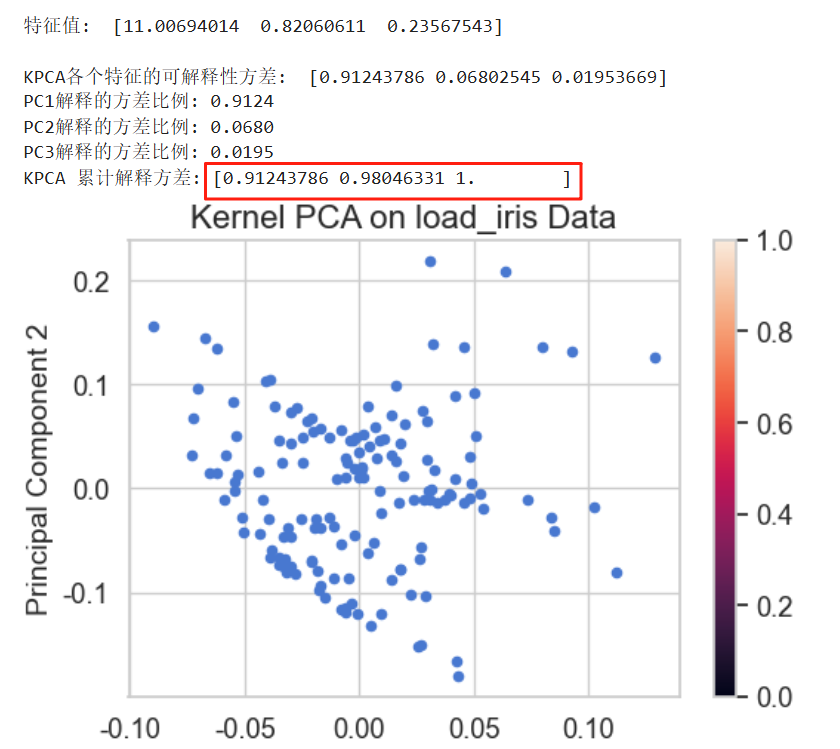

KPCA 对比PCA

PCA的代码实现

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler 
from matplotlib.patches import Ellipse
import seaborn as sns
plt.rcParams['font.sans-serif'] = ['SimHei']#解决图表中中文显示问题
plt.rcParams['axes.unicode_minus']=False# 解决图表中负号不显示问题
import warnings
warnings.filterwarnings("ignore")
# 设置Seaborn风格
sns.set(style="whitegrid", palette="muted", font_scale=1.2)# 加载Iris数据集
data = load_iris()
X = data.data  # 特征矩阵
y = data.target  # 标签
target_names = data.target_namesfrom sklearn.preprocessing import StandardScaler  
scaler = StandardScaler() 
X_scaled = scaler.fit_transform(X)# PCA降维
pca = PCA(n_components=3)  # n_components=3表示降到3维，也可以 n_components=0.9 表示需要保留多少信息确定需要降到多少维
X_pca = pca.fit_transform(X_scaled)
# 可视化
plt.figure(figsize=(6,4))
plt.scatter(X_pca[:, 2], X_pca[:, 1], cmap=plt.cm.Spectral, s=20)
plt.title(' PCA on load_iris Data', fontsize=16)
plt.xlabel('Principal Component 1', fontsize=14)
plt.ylabel('Principal Component 2', fontsize=14)
plt.colorbar()
plt.grid(True)
plt.show()print('维数：',pca.n_components_)
# print('保留原数据90%的信息需要的维数：',pca.n_components_)# 各个特征的可解释性方差
eigenvalues = pca.explained_variance_
eigenvecs = pca.components_.T
print(f'\n特征值: ',eigenvalues)
#单位特征向量
print(f'特征值对应的单位特征向量:\n ',eigenvecs)explained_variance_ratio = pca.explained_variance_ratio_
print(f'\n各个特征的可解释性方差: ',explained_variance_ratio)
print(f'PC1解释的方差比例: {explained_variance_ratio[0]:.4f}')
print(f'PC2解释的方差比例: {explained_variance_ratio[1]:.4f}')
print(f'PC3解释的方差比例: {explained_variance_ratio[2]:.4f}')
# print(f'PC4解释的方差比例: {explained_variance_ratio[3]:.4f}')cumulative_variance = np.cumsum(explained_variance_ratio)
print("PCA 各成分解释方差比例:", cumulative_variance)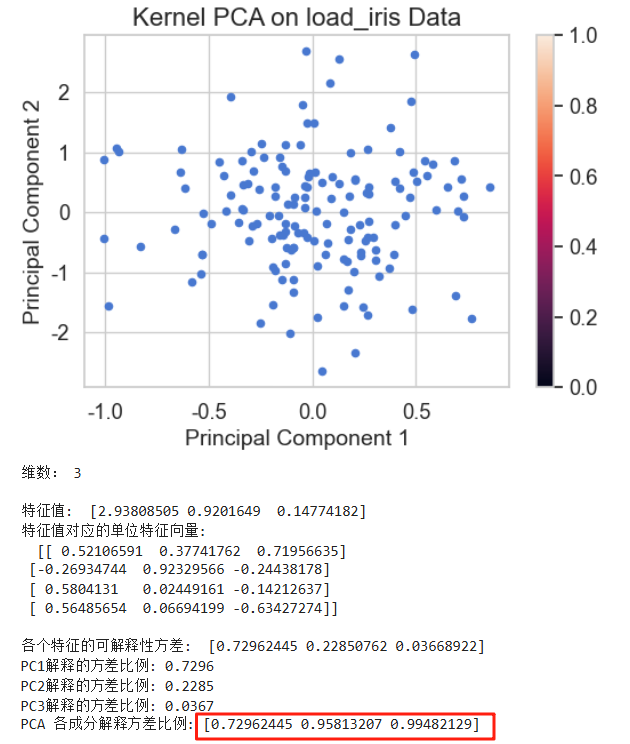

同样的数据，分别在KPCA和PCA上进行降维，KPCA的各成分解释方差比例高于PCA的各成分解释方差比例。

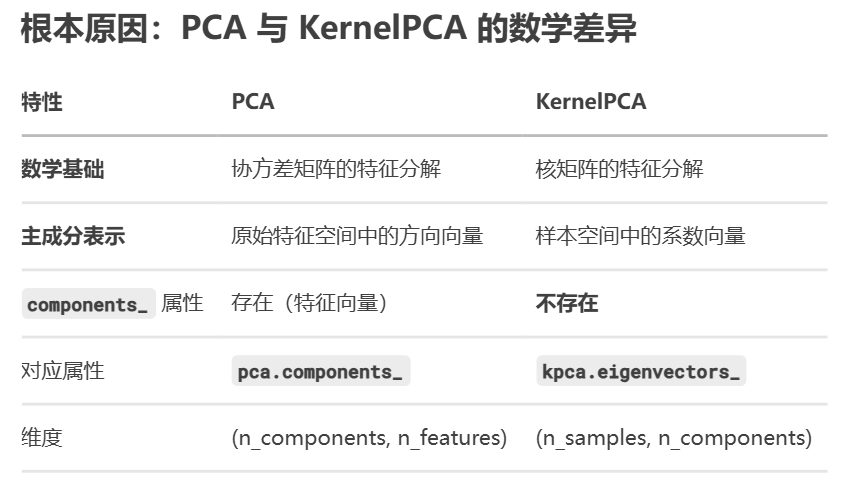
注意：在PCA时有计算特征值对应的单位特征向量，而KPCA没有，即KernelPCA 没有 components_，原因有以下三点：
- 隐式特征空间
KernelPCA 通过核函数将数据映射到高维（甚至无限维）特征空间
这个空间中的主成分方向（特征向量）无法显式表示为原始特征的组合
- 基于样本的表示
解的形式为：$V_k={\sum }_{i=1}^n{\alpha }_i^{(k)}\varphi (x_i)$
主成分方向被表示为训练样本的线性组合，而非原始特征的组合
- 无限维问题
对于 RBF 等核函数，特征空间是无限维的
无法获得有限维的 components_ 向量

解决KPCA没有特征向量这一问题，计算特征向量系数（替代 components_），下面是实现代码

eigenvectors = kpca.eigenvectors_print("特征向量系数矩阵形状:", eigenvectors.shape)
print("前5个样本在第一主成分上的系数:\n", eigenvectors[:5, 0])
print("第一主成分上的系数:\n", eigenvectors[:, 0])  # 对于第k个主成分，eigenvectors[:, k]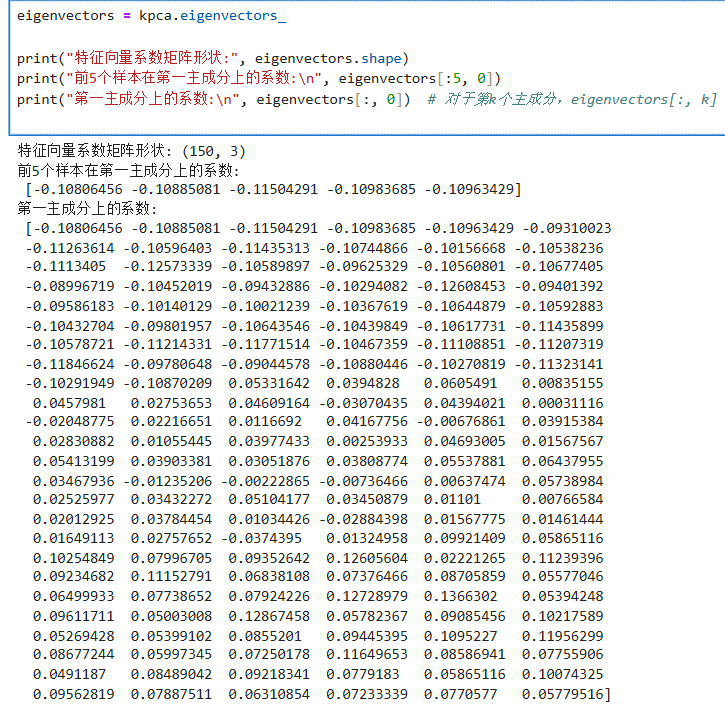

Python手写核主成分分析

手写核主成分的python代码参考上文