激活函数篇(2):SwiGLU | GLU | Swish | ReLU | Sigmoid
参考视频:3分钟理解SwiGLU激活函数_哔哩哔哩_bilibili
激活函数篇一链接:激活函数(Sigmoid | Tanh | ReLU | Leaky ReLU | Parametric ReLU)-CSDN博客
Sigmoid
公式为:
输出范围是 [0,1]
优点
平滑且连续。
输出值范围在 [0,1],可以很好地解释为概率值。
缺点
梯度消失问题:在输入值较大或较小时,Sigmoid 函数的梯度接近于零,导致权重更新很慢,在深层网络中难以传播有效的梯度信号。
不易收敛:输出总是正值,不是零中心,这可能导致权重更新时的效率较低。
应用场景:(1)用于二分类输出层,因为其输出值是 [0,1],可以解释为概率;(2)用于简单模型中作为隐藏层激活函数。
ReLU(Rectified Linear Unit)
公式为:
优点
简单高效:只需判断输入是否大于零,计算成本很低。
解决梯度消失问题:当 x>0时,梯度恒为 1,因此它在反向传播中可以很好地传播梯度。
稀疏激活:ReLU 的输出中有大量的零值(当 x≤0时),可以引入稀疏性,有助于特征筛选。
缺点
死亡 ReLU 问题:当 x≤0 时,梯度为零,可能导致权重无法更新,某些神经元“死亡”且永远不会被激活。
对输入分布的敏感性较高。
Swish 或 SILU(Sigmoid Weighted Linear Unit)
公式为:
当β=1时,
优点
平滑输出:Swish 是一个平滑的激活函数,相比 ReLU 的分段线性结构,Swish 的非线性表现更强。
没有零死区:在 −∞<x<∞ 时,Swish 始终可导。
Swish 在一些现代神经网络中(如 EfficientNet)表现优于 ReLU,特别是在深层网络中。
缺点
计算复杂度稍高于 ReLU;
理论上 Swish 的性能依赖于输入分布,在某些情况下可能并不优于 ReLU。
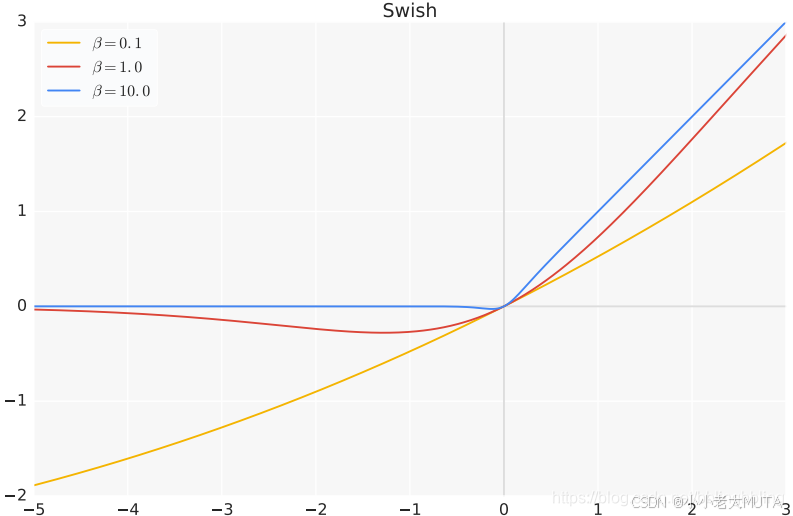
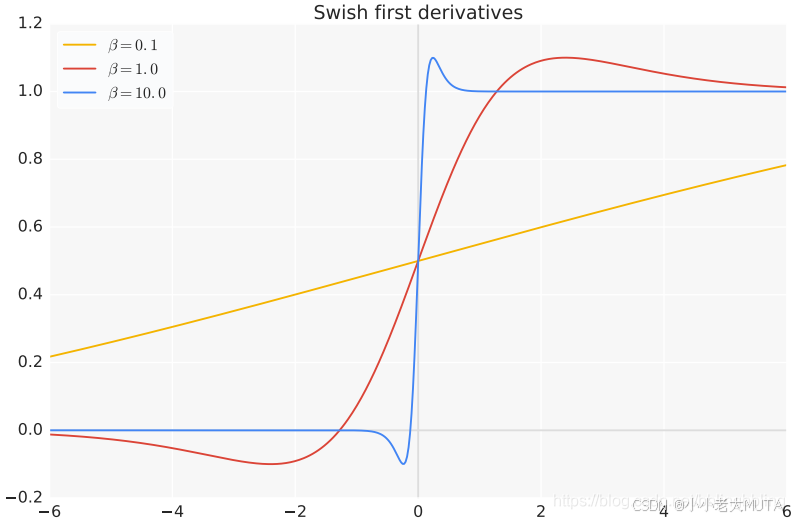
参考链接:swish激活函数_swish函数-CSDN博客
其实针对死亡ReLU问题,Leaky ReLU也对其做了简单的改进,即直接在负半轴引入一个小的斜率,解决了 ReLU 在负数输入区域的梯度为零的问题。这意味着即使在负值区域,Leaky ReLU 也能传递一些梯度,防止神经元在训练过程中“死亡”。
Swish 更复杂,具有非单调性和光滑性,通常能在复杂任务中提供更好的表现。
GLU(Gated Linear Unit)
GLU 是门控线性单元,通常用在 Transformer、语言模型等深度学习模型中。公式为:
- x 是输入向量。
- W 和 V 是权重矩阵。
- σ 是 Sigmoid 激活函数。
- ⊙ 表示元素乘法(Hadamard 乘积),即对应元素相乘。
输入 x 被分别与两个不同的权重矩阵 W 和 V 相乘,得到两个不同的线性变换结果。
门控机制
计算 σ(xW):首先,输入 x 通过权重 W 进行线性变换,然后通过 Sigmoid 激活函数。这部分输出的值在 [0,1] 范围内,充当“门”的作用,控制信息流的多少。
计算(xV):输入 x 通过权重 V 进行线性变换,得到主要信息流。
优点
门控机制:动态地控制 信息流动。
高效的表示能力:GLU 的设计有效融合了线性部分和非线性部分。
缺点
增加模型参数量,因为需要两倍的输入维度;
计算复杂度较高。
应用场景:在语言模型(如 Transformer)中,GLU 常作为激活函数使用,能够有效提升表达能力。用于捕获特征间的复杂关系。
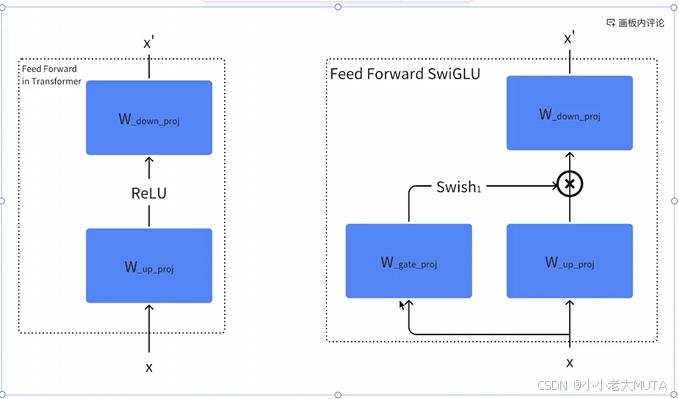
SwiGLU
SwiGLU = Swish + GLU
公式为:
优点
更高的非线性表现:Swish 的组合使得激活函数对输入特征更敏感。
动态门控能力增强:相比 GLU,SwigLU 可以更好地捕获复杂关系。
缺点
计算复杂度进一步提高。
增加了输入维度和模型参数量。
应用场景:SwigLU 是 Transformer 和语言模型中常用的一种激活函数,特别是在深度学习模型中(如 GPT、BERT)表现优异。适合高维空间的特征选择和复杂关系建模。