当前位置：首页 > news >正文

多重时间聚合算法(MAPA)改进需求预测模型

news 2025/8/12 11:50:41

这篇文章Improving your forecasts using multiple temporal aggregation介绍了“多重聚合预测算法”（MAPA）。它指出传统预测常依赖单一数据频率，但MAPA通过将数据聚合到不同时间粒度（如日、周、月、年）并分别建模，然后组合这些预测。

组合这些预测的方法主要有以下几种，直接组合预测结果：

计算平均值（Averages）：将来自不同聚合级别的预测值直接取平均。
计算中位数（Medians）：将来自不同聚合级别的预测值取中位数，文章提到这更适合避免极端值的影响。
使用截尾均值（Trimmed Means）：这是一种更稳健的平均方法，排除最高和最低的预测值后再计算平均。
使用其他操作符（Other operators）：文章泛指除了平均值和中位数之外的其他组合方法。

组合模型组件（针对季节性问题）：

为了避免季节性被过度抑制，文章建议不直接组合最终预测，而是组合模型的各个组成部分。
具体做法是：

先组合来自不同聚合级别的所有**水平（Level）**估计。
然后组合所有**趋势（Trend）**估计。
再组合所有**季节性（Seasonal）**估计（只考虑允许季节性建模的聚合级别）。
最后，使用这些组合后的组件来计算最终的预测值。

文章目录

0 前言
1 不同时间粒度最优模型也有弊端
2 多重聚合预测算法 (MAPA)具体操作
- 2.1 步骤 1：聚合
- 2.2 步骤 2：预测
- 2.3 步骤 3：组合
3 季节性问题
4 这么多计算步骤是否值得？
5 不仅仅是准确性
6 R 语言依赖
7 延伸阅读

0 前言

在大多数商业预测应用中，问题通常会直接决定我们收集和用于预测数据时的采样频率。传统方法试图从历史观测中提取信息来构建预测模型。本文将探讨如何通过时间聚合来转换数据，从而获取有关现有序列的额外信息，最终实现更优的预测。我们将讨论一种新引入的建模方法，它结合了来自许多不同时间聚合级别的信息，在此过程中增强了序列的各种特征，从而生成稳健且准确的预测。

时间聚合有助于识别序列特征，因为这些特征在不同频率下会得到增强。此外，这个简单的技巧可以减少间歇性，使得成熟的传统预测方法能够用于慢速移动数据。
使用多个时间聚合级别可以显著提高预测性能，特别是对于较长的预测期，因为序列的各种长期组成部分能够得到更好的捕捉。
跨不同聚合级别的组合可以生成在所有频率上都协调一致的估计。从实践者的角度来看，这非常重要，因为它生成的预测在操作、战术和战略层面都是协调一致的。
相关的 R 软件包 MAPA 允许通过开源 R 统计软件在实践中直接使用此算法。

通常，对于短期操作预测，会使用月度、每周甚至每日数据。另一方面，常见的建议是使用季度和年度数据来生成长期预测。这类数据包含的细节较少，并且通常更平滑，能更好地展现序列的长期行为。当然，从不同频率序列生成的数据必然会有所不同，这常常导致某个时期的累积操作预测与同期累积需求派生出的战术或战略预测不一致。尽管如此，在实践中，最常见的情况是使用相同的数据和模型来生成短期和长期预测，这存在明显的局限性，特别是对于长期预测。

数据的不同频率可以揭示或隐藏各种时间序列特征。当考虑快速移动时间序列时，随机变动和季节性模式在每日、每周或每月数据中更为明显。通过使用非重叠时间聚合，可以轻松构建低频率时间序列。聚合级别指的是时间聚合过程中时间桶的大小，并与数据的频率直接相关。聚合级别的增加会导致序列频率的降低。同时，这个过程也充当了一个滤波器，平滑高频特征，并更好地近似数据的长期组成部分，例如水平、趋势和周期。请注意图 1 中序列在不同聚合级别下的变化。原始的月度序列主要受季节性成分影响，而在第 12 级聚合（现在是年度序列）下，则主要受水平变化和微弱趋势的影响。

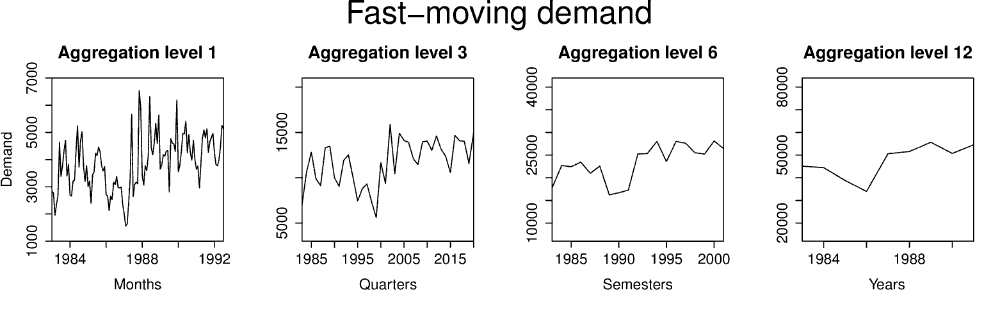
图 1. 月度快速移动时间序列在不同非重叠时间聚合级别下的表现。

在间歇性需求数据（就是应季产品）的情况下，从高频（月度）数据转向低频（年度）数据可以减少（甚至消除）数据的间歇性，从而最大限度地减少需求为零的时期数量。这使得传统预测方法可以应用于该问题。图 2 展示了这类时间序列如何随着聚合级别的变化而改变行为。

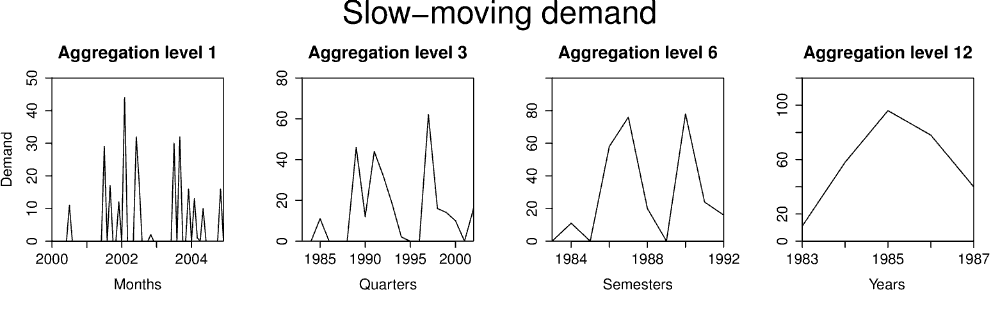
图 2. 月度慢速移动时间序列在不同非重叠时间聚合级别下的表现。

这些时间序列特征的存在和大小，无论是对于快速移动还是慢速移动的商品，都会影响预测准确性。因此，对于实践中的预测员来说，显而易见的问题是：“我应该使用哪个聚合级别的数据？”

1 不同时间粒度最优模型也有弊端

你把数据“打包”成不同的样子（比如按月打包、按季打包），然后分别去找到一个“最厉害”的预测模型。但你找到的这个“最厉害”的模型，可能只是在这个特定的“打包方式”下看起来厉害。

由于时间序列特征会随着数据频率（或聚合级别）的变化而变化，因此不同的方法将被识别为最优。这些方法将产生不同的预测，最终导致不同的决策。本质上，我们必须处理真正的模型不确定性，即在特定数据聚合级别下被识别为最优模型的适用性或错误指定问题。
即使我们忽略时间聚合问题，对于简单的时间序列，我们也有两种主要的不确定性：

i) 数据不确定性：我们是仅仅非常幸运，还是非常不幸地拥有了我们现有的样本？随着更多观测值的出现，我们的模型及其参数将如何变化？
ii) 模型不确定性：模型或其参数是否合适，或者由于潜在的优化问题，模型提供了糟糕的预测？

第二个问题对于 [具有许多自由度的模型]而言更为严重。时间聚合揭示了这些差异，并迫使我们面对这个问题。

解决这个问题的一个潜在方法是，通过使用多个聚合级别来尝试考虑数据的所有替代视图，从而减少上述不确定性。然后分别对每个视图进行建模，最好地捕捉在每个级别上被放大的不同时间序列特征。由于模型会不同，与其偏爱单一模型，不如将它们（或它们的预测）组合成一个稳健的最终预测，该预测考虑了来自所有数据频率的信息。

因此，我们建议不要相信单一聚合级别上的单一模型，这不可避免地会导致选择一个单一的“最优”模型。相反，请考虑多个聚合级别。这种方法试图降低选择一个基于单一数据视图的糟糕模型的风险，从而减轻了模型选择的重要性。

2 多重聚合预测算法 (MAPA)具体操作

在本节中，我们将通过三个步骤（聚合、预测和组合）解释如何在实践中应用所提出的多重聚合预测算法 (MAPA)。图 3 展示了所提出框架的图形说明，并将其与实践中通常应用的标准预测方法进行了对比。

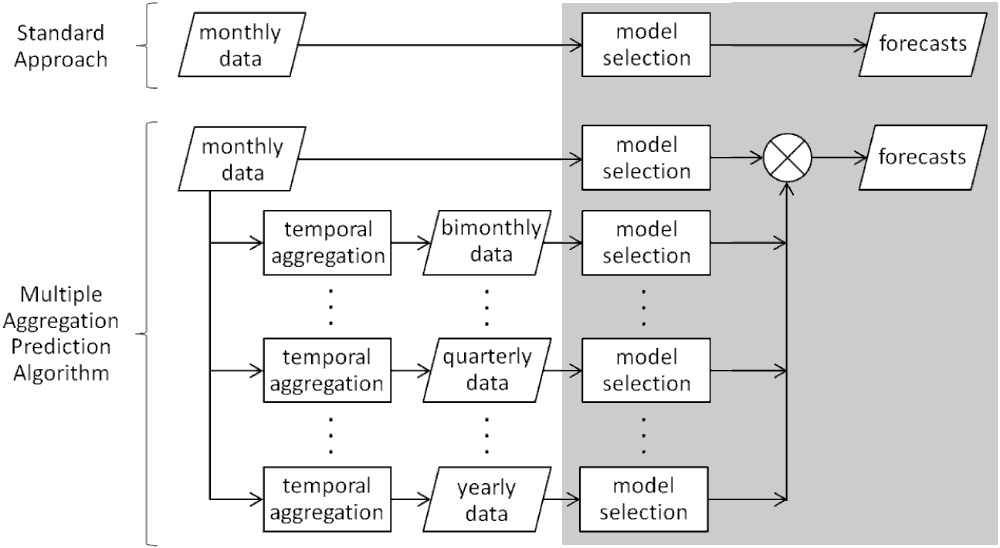
图 3. 标准预测方法与 MAPA 预测方法的对比。

2.1 步骤 1：聚合

在标准方法中，统计预测方法的输入是单一频率的数据，通常是数据收集过程中使用的采样频率，或者后续将用于预测的频率。因此，聚合级别要么由数据可用性驱动，要么由预测的预期用途驱动。另一方面，MAPA 使用同一数据的多个实例，这些实例对应于不同的频率或聚合级别。假设我们有 4 年的月度观测数据（48 个数据点）。为了将这些数据转换为季度数据（1 季度 = 3 个月），我们定义 48/3 = 16 个时间桶。然后，我们使用简单的求和进行聚合，以计算每个时间桶的累积需求。这个过程将创建 16 个聚合观测值，这些观测值将与所需的季度频率匹配。在这种情况下，聚合级别等于 3 个周期，而转换后的频率等于原始频率的 1/3。

如果所选的聚合级别不是原始频率下可用观测值的倍数，那么在此时间聚合过程中可能会丢弃一些数据点。继续我们之前的例子，如果聚合级别设置为 5，那么只能定义 9 个时间桶，对应 45 个月度观测值。在这种情况下，有 3 个月度周期被丢弃。我们选择从序列的开头丢弃观测值，因为后面的观测值被认为更具相关性。

这种将原始数据转换为替代（较低）频率的过程，使用多个聚合级别，只要所有转换后的序列都有足够的数据来生成统计预测，就可以继续进行。如果原始采样频率是月度数据，并且考虑到公司通常保留 3 到 5 年的历史数据，我们建议聚合过程一直持续到年度频率（聚合级别等于 12 个周期）。这也将足以突出序列的长期变化。

无论如何，虽然起始频率总是受原始数据采样的限制，但我们建议聚合的上限应至少达到年度级别，在该级别上，季节性将从数据中完全过滤掉，而长期（低频）成分（如趋势）将占据主导地位。当然，聚合级别的范围应包含与预测预期用途相关的级别：例如，用于 S&OP 的月度预测，或用于长期规划的年度预测。这确保了最终的 MAPA 预测捕获所有相关的时间序列特征，从而提供时间上协调一致的预测。

第一步的输出是一组序列，所有序列都对应相同的基本数据，但转换为不同的频率。

2.2 步骤 2：预测

在步骤 1 中计算的每个序列都应单独进行预测。在预测文献中，存在几种自动模型选择协议。对于快速移动商品，指数平滑被认为是可靠且相对准确的。它对应于可能包含趋势（阻尼或不阻尼）和季节性的模型，同时允许多种形式的交互（加性或乘性）。一种广泛使用的方法是根据预定义信息准则（如 AIC）的最小化来自动选择最佳模型形式。预计在我们的序列集中，将在不同的聚合级别上选择不同的模型。季节性和各种高频成分预计将在较低聚合级别（如月度数据）上得到更好的建模，而长期趋势将在频率降低（年度数据）时得到更好的捕捉。

在间歇性需求序列的情况下，存在分类方案，允许在两种最广泛使用的预测方法之间进行选择：Croston 方法和 Syntetos-Boylan 近似 (SBA)。在此类方案下，间歇性水平和需求变异性决定了哪种方法更合适。使用多个聚合级别将改变间歇性和变异性，因此我们预计在所有频率上都将识别出不同的最优方法。此外，在较高聚合级别上，生成的序列可能不包含零需求期。在这些情况下，我们建议使用传统优化的简单指数平滑，利用其在非间歇性时间序列中的良好性能。此外，将数据从慢速移动转换为快速移动可能会揭示在较低粒度级别（噪声是主要成分）可能不存在的常规时间序列成分（如趋势或季节性）。任何采样频率足够高的时间序列都是间歇性的，因此这些情况应被视为一个连续体。

此步骤的输出是多组预测，每组对应一个替代频率。

2.3 步骤 3：组合

所提出的 MAPA 方法的最后阶段涉及将从替代频率派生出的不同预测进行适当组合。

在能够组合从各种频率生成的预测之前，我们需要将它们转换回原始频率。虽然从较低聚合级别聚合预测很简单，但分解可能更复杂。文献中讨论了许多替代策略，然而，简单地将一个观测值在高频率级别上分成相等的部分已被证明非常有效且易于使用。例如，假设在预测步骤之后，我们有一些季度频率的聚合预测。为了将这些点预测中的每一个转换回原始（月度）频率，我们只需将它们除以三，并将相同的值用于所有三个月。因此，一月份的预测将与二月或三月的预测相同，并且所有这些都将等于第一季度预测除以 3。

**一旦来自各种聚合级别的所有预测都被转换回原始频率，它们随后将被组合成最终预测。组合可以通过计算平均值、中位数或使用其他运算符（例如预测的截尾均值）来完成。**我们发现平均值和中位数都表现良好，尽管后者更适合确保组合后的最终预测不受极端值的影响。

预测的预期用途可能与数据采样频率不同。或者，可能需要来自各种聚合级别的预测用于操作、战术或战略规划。为了实现这一点，只需将最终预测聚合到所需的级别。MAPA 预测的一个便利特性是它们适用于所有这些级别，因为它们包含所有级别的信息。因此，在各种聚合级别上的此类预测是时间上协调一致的，不再需要费心去确保这些预测一致，否则这些预测通常会有所不同。

3 季节性问题

上述算法应用中出现的一个问题是关于时间序列季节性成分的极端阻尼。考虑月度数据转换为所有频率直到年度的情况。如果原始序列是季节性的，那么季节性将只在聚合级别 1（对应原始频率）、2、3、4 和 6 上进行建模。同时，季节性将不会在考虑的其他任何聚合级别上进行建模，无论是分数的还是完全过滤掉的。

计算所有级别预测的简单组合将本质上抑制季节性模式。这在图 4 中有所体现，其中一个带有季节性（红色）和一个不带季节性（绿色）的模型被组合，结果预测的拟合效果很差，原因是季节性被抑制了。

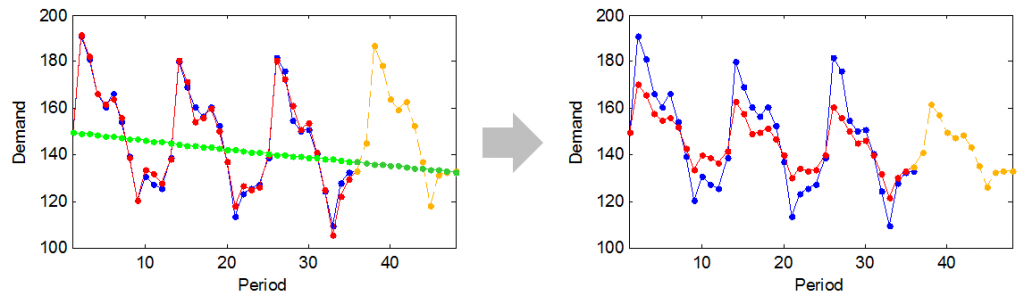
图 4. 由于预测组合导致的季节性成分阻尼示例。

为了解决这个问题，组合应该在模型组件上进行，而不是在预测上。当使用指数平滑系列方法时，这很简单，因为它分别为每个组件（水平、趋势和季节性）提供估计。季节性组件的组合将只考虑允许季节性的聚合级别（1、2、3、4 和 6）。另一方面，水平和趋势将在每个级别上建模。如果在一个级别上选择了没有趋势的模型，那么该聚合级别的趋势组件等于零。因此，不是组合预测，而是必须首先组合来自各种聚合级别的所有水平估计，然后是所有趋势估计，然后是季节性估计。然后使用得到的组合组件来计算最终预测，就像使用传统指数平滑一样。

解决这个建模问题的其他方法包括只考虑部分聚合级别或引入可以处理分数季节性的模型。

4 这么多计算步骤是否值得？

简短的回答是：值得！MAPA 方法已在快速移动和慢速移动需求数据上进行了测试，与传统方法相比，提供了改进的预测性能。

更具体地说，所提出的方法在准确性和偏差方面都提供了更好的估计。在快速移动数据的情况下，MAPA 在大多数数据频率上都优于指数平滑，尤其在长期预测方面非常准确。这是在高聚合级别上拟合模型的直接结果，在该级别上，序列的水平和长期趋势得到了最佳识别。在慢速移动数据的情况下，MAPA 在增强选择方案（Croston-SBA-SES）下，与任何单一方法相比表现更好，同时其性能也优于原始选择方案（Croston-SBA）。

除了 MAPA 在预测性能上的任何改进之外，该算法的另一个优点是决策者无需预先选择单一聚合级别。虽然在某些情况下，将聚合级别设置为等于提前期加上评审期是有意义的，但消除此超参数可以被视为一个优势，从而简化了预测过程。

5 不仅仅是准确性

尽管使用 MAPA 可以带来准确性和鲁棒性方面的优势，但其主要优势在于组织层面。结合多个时间聚合级别（从而捕获高频和低频成分）可以为短期和（特别是）长期预测带来更准确的结果。最重要的是，这种策略提供了在所有频率上都协调一致的预测，这适用于协调操作、战术和战略决策。这对于实践非常有用，因为相同的预测可以用于所有三个规划级别。

因此，预测和决策是协调一致的，不再需要更改或偏爱来自特定级别的预测，而这在实践中通常是临时进行的，并会产生有害影响。这是朝着“单一数字”预测迈出的重要一步，即多个决策和组织职能都基于对未来的相同看法，从而使它们保持一致。

在实践中，短期操作预测（驱动需求规划和库存管理）与长期预算预测不兼容的情况并不少见。MAPA 通过在各种规划期内提供单一协调视图来解决这个问题。这仅仅是在工业环境中实现完全协调预测的第一步。跨部门协调以及不同利益相关者的有效互动和沟通只是同一问题的其余方面。