LeetCode151~188题解
LeetCode151.翻转字符串里的单词:
题目描述:
给你一个字符串 s ,请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意:输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
示例 1:
输入:s = “the sky is blue”
输出:“blue is sky the”
示例 2:
输入:s = " hello world "
输出:“world hello”
解释:反转后的字符串中不能存在前导空格和尾随空格。
示例 3:
输入:s = “a good example”
输出:“example good a”
解释:如果两个单词间有多余的空格,反转后的字符串需要将单词间的空格减少到仅有一个。
提示:
1 <= s.length <= 10^4
s 包含英文大小写字母、数字和空格 ’ ’
s 中 至少存在一个 单词
进阶:如果字符串在你使用的编程语言中是一种可变数据类型,请尝试使用 O(1) 额外空间复杂度的 原地 解法。
思路:
1.先翻转单个单词 2.翻转整个字符串
细节:去掉多余空格,每个单词中间要加空格,最后一个单词不加空格
时间复杂度:每个字符遍历一次,时间复杂度为O(n)
注释代码:
class Solution {
public:string reverseWords(string s) {int k = 0;for(int i = 0; i < s.size(); i++){if(s[i] == ' ') continue; //排除掉所有空格int j = i, t = k;while(j < s.size() && s[j] != ' ') s[t++] = s[j++]; //重整s串,将一个个单词截出来reverse(s.begin() + k, s.begin() + t); //翻转单个单词s[t++] = ' '; //在每个单词后面加空格k = t, i = j; //k是每个单词的起始位置,i跳过上个单词往后继续循环}if(k) k--; //k> 0说明至少存在一个单词,那么需要将最后一个空格删除s.erase(s.begin() + k, s.end()); //将k后面的删除reverse(s.begin(), s.end()); //最后将整个字符串翻转return s;}
};
纯享版:
class Solution {
public:string reverseWords(string s) {int k = 0;for(int i = 0; i < s.size(); i++){if(s[i] == ' ') continue;int j = i, t = k;while(j < s.size() && s[j] != ' ') s[t++] = s[j++];reverse(s.begin() + k, s.begin() + t);s[t++] = ' ';k = t, i = j;}if(k) k--;s.erase(s.begin() + k, s.end());reverse(s.begin(), s.end());return s;}
};LeetCode152.乘积最大子数组:
题目描述:
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续
子数组
(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
1 <= nums.length <= 2 * 10^4
-10 <= nums[i] <= 10
nums 的任何子数组的乘积都 保证 是一个 32-位 整数
思路:
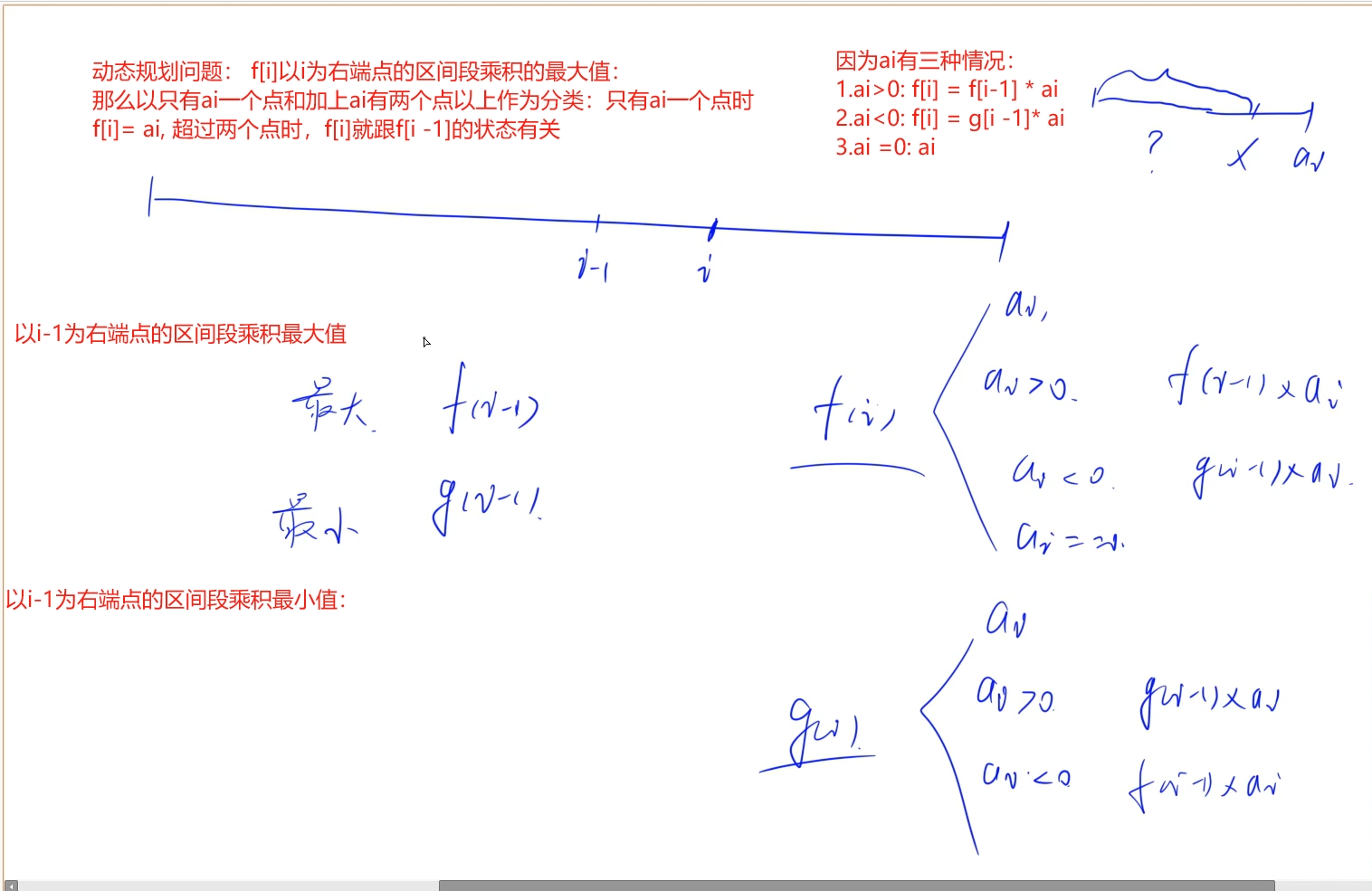
动态规划思想: 设定集合f[i]表示以i为右端点的区间段的乘积的最大值, 分类则为仅包含ai和两个端点以上的区间段的乘积的最大值也就是f[i - 1]* ai的情况,针对ai的情况又进行分类讨论
时间复杂度:

注释代码:
class Solution {
public:int maxProduct(vector<int>& nums) {int res = nums[0];int f = nums[0], g = nums[0]; //均从第一个数组元素开始for(int i = 1; i < nums.size(); i++){int a = nums[i], fa = f * a, ga = g * a; //只管求出fa和gaf = max(a, max(fa, ga)); //最后f只需要取三种情况的最大值即可g = min(a, min(fa, ga)); //g只需要取三种情况的最小值即可res = max(res, f); }return res;}
};
纯享版:
class Solution {
public:int maxProduct(vector<int>& nums) {int f = nums[0], g = nums[0];int res = nums[0];for(int i = 1; i < nums.size(); i++){int a = nums[i], fa = f * a, ga = g * a;f = max(a, max(fa, ga));g = min(a, min(fa, ga));res = max(res, f);}return res;}
};LeetCode 153.寻找旋转排序数组中的最小值:
题目描述:
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 3 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:
n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 中的所有整数 互不相同
nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
思路:
首先判断是否经过旋转,如果严格升序的就直接返回nums[0]即可,否则的话通过nums[0]将整个区间二分,最后二分的位置即是最小值的位置
时间复杂度:
题目要求时间复杂度O(logn),看到O(logn)思考相应的算法
代码:
class Solution {
public:int findMin(vector<int>& nums) {int l = 0, r = nums.size() -1;if(nums[r] > nums[l]) return nums[l];while(l < r){int mid = l + r >> 1;if(nums[mid] < nums[0]) r = mid;else l = mid + 1;}return nums[r];}
};LeetCode154.寻找旋转排序数组中的最小值Ⅱ:
题目描述:
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,4]
若旋转 7 次,则可以得到 [0,1,4,4,5,6,7]
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个可能存在 重复 元素值的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须尽可能减少整个过程的操作步骤。
示例 1:
输入:nums = [1,3,5]
输出:1
示例 2:
输入:nums = [2,2,2,0,1]
输出:0
提示:
n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
进阶:这道题与 寻找旋转排序数组中的最小值 类似,但 nums 可能包含重复元素。允许重复会影响算法的时间复杂度吗?会如何影响,为什么?
思路:
跟上题思路一致,不过存在重复元素的影响就是在进行区间二分时,可能不好分,因为前后的元素一样的话,无法判断当前中间点是符合哪一段从而更新区间,所以需要先将前后可能存在的重复元素删除,再进行二分
时间复杂度:
最坏的情况下可能全部元素都一样,那么全部都要遍历一遍,所以总的时间复杂度为O(n)
注释代码:
class Solution {
public:int findMin(vector<int>& nums) {int l = 0, r = nums.size() -1;while(l < r && nums[l] == nums[r]) r--; //将最后面跟开头相同的重复元素删除if(nums[l] < nums[r]) return nums[l]; //如果整个区间都是升序的,直接返回第一个数while(l < r){int mid = l + r >> 1;if(nums[mid] < nums[0]) r = mid;else l = mid + 1;}return nums[r];}
};纯享版:
class Solution {
public:int findMin(vector<int>& nums) {int l = 0, r = nums.size() - 1;while(l < r && nums[l] == nums[r]) r--;if(nums[l] < nums[r]) return nums[l];while(l < r){int mid = l + r >> 1;if(nums[mid] < nums[0]) r = mid;else l = mid + 1;}return nums[l];}
};LeetCode155.最小栈:
题目描述:
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。
示例 1:
输入:
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
提示:
-2^31 <= val <= 2^31 - 1
pop、top 和 getMin 操作总是在 非空栈 上调用
push, pop, top, and getMin最多被调用 3 * 10^4 次
思路:
最简单的思路就是使用两个栈,一个存储每个数:数值栈,另外一个同步存储每次操作的最小值:最小栈 -> f(i) = min(f(i - 1), ai)(简单DP)
优化思路:
当准备插入的数ai大于维护最小值的栈顶f(i - 1)时,可以不存储f(i)的值,因为f(i)就为f(i -1), 问题是当删除数值栈的栈顶时,怎么才能判断需不需要删除当前最小栈的栈顶,这里我们可以分析,当ai > 最小栈的栈顶时,我们是不存储f(i)的,也就是我们只需要判断数值栈的栈顶小于等于最小栈栈顶就应该删除最小栈栈顶,因为当数值栈栈顶大于最小栈栈顶时说明最小栈栈顶存储的不是f(i)
时间复杂度:
单个元素进栈出栈都是O(1)的,所以时间复杂度为O(1)
优化前:
class MinStack {
public:stack<int> stk, f; //f维护从前往后插入的数的最小值MinStack() {}void push(int x) {stk.push(x); //栈中插入xif(f.empty()) f.push(x);else f.push(min(f.top(), x));}void pop() {f.pop();stk.pop();}int top() {return stk.top();}int getMin() {return f.top();}
};/*** Your MinStack object will be instantiated and called as such:* MinStack* obj = new MinStack();* obj->push(val);* obj->pop();* int param_3 = obj->top();* int param_4 = obj->getMin();*/优化后:
class MinStack {
public:stack<int> stk, f; //f维护从前往后插入的数的最小值MinStack() {}void push(int x) {stk.push(x); //栈中插入xif(f.empty() || f.top() >= x) f.push(x); //如果f栈顶大于x则说明需要将x存入最小栈}void pop() {if(stk.top() <= f.top()) f.pop(); //如果最后插入的数小于最小栈的栈顶则需要移除最小栈的栈顶stk.pop();}int top() {return stk.top();}int getMin() {return f.top();}
};/*** Your MinStack object will be instantiated and called as such:* MinStack* obj = new MinStack();* obj->push(val);* obj->pop();* int param_3 = obj->top();* int param_4 = obj->getMin();*/纯享版:
class MinStack {
public:stack<int> stk1, stk2;MinStack() {}void push(int val) {stk1.push(val);if(stk2.empty() || stk2.top() >= val) stk2.push(val);}void pop() {if(stk1.top() <= stk2.top()) stk2.pop();stk1.pop();}int top() {return stk1.top();}int getMin() {return stk2.top();}
};/*** Your MinStack object will be instantiated and called as such:* MinStack* obj = new MinStack();* obj->push(val);* obj->pop();* int param_3 = obj->top();* int param_4 = obj->getMin();*/LeetCode160.相交链表:
题目描述:
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
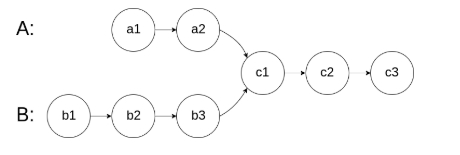
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal - 相交的起始节点的值。如果不存在相交节点,这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中(从头节点开始)跳到交叉节点的节点数
skipB - 在 listB 中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:
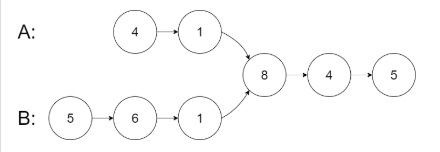
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at ‘8’
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
— 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:
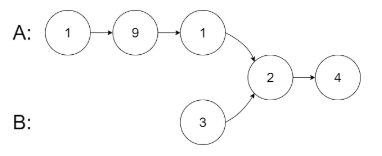
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at ‘2’
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
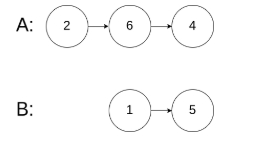
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:No intersection
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
提示:
listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 10^4
1 <= Node.val <= 10^5
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点,intersectVal 为 0
如果 listA 和 listB 有交点,intersectVal == listA[skipA] == listB[skipB]
进阶:你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案?
思路:
链表A长度为m,链表B长度为n, 假设相交点距离headA为a, 距离headB为b, 共同长度为c, 那么我们只需要让两个指针分别走过对应链表后换到另外一条链表从头开始走,最后两个指针肯定会相遇在相交点,或者都停在链表尾部,因为: a + c + b = b + c + a,如图:
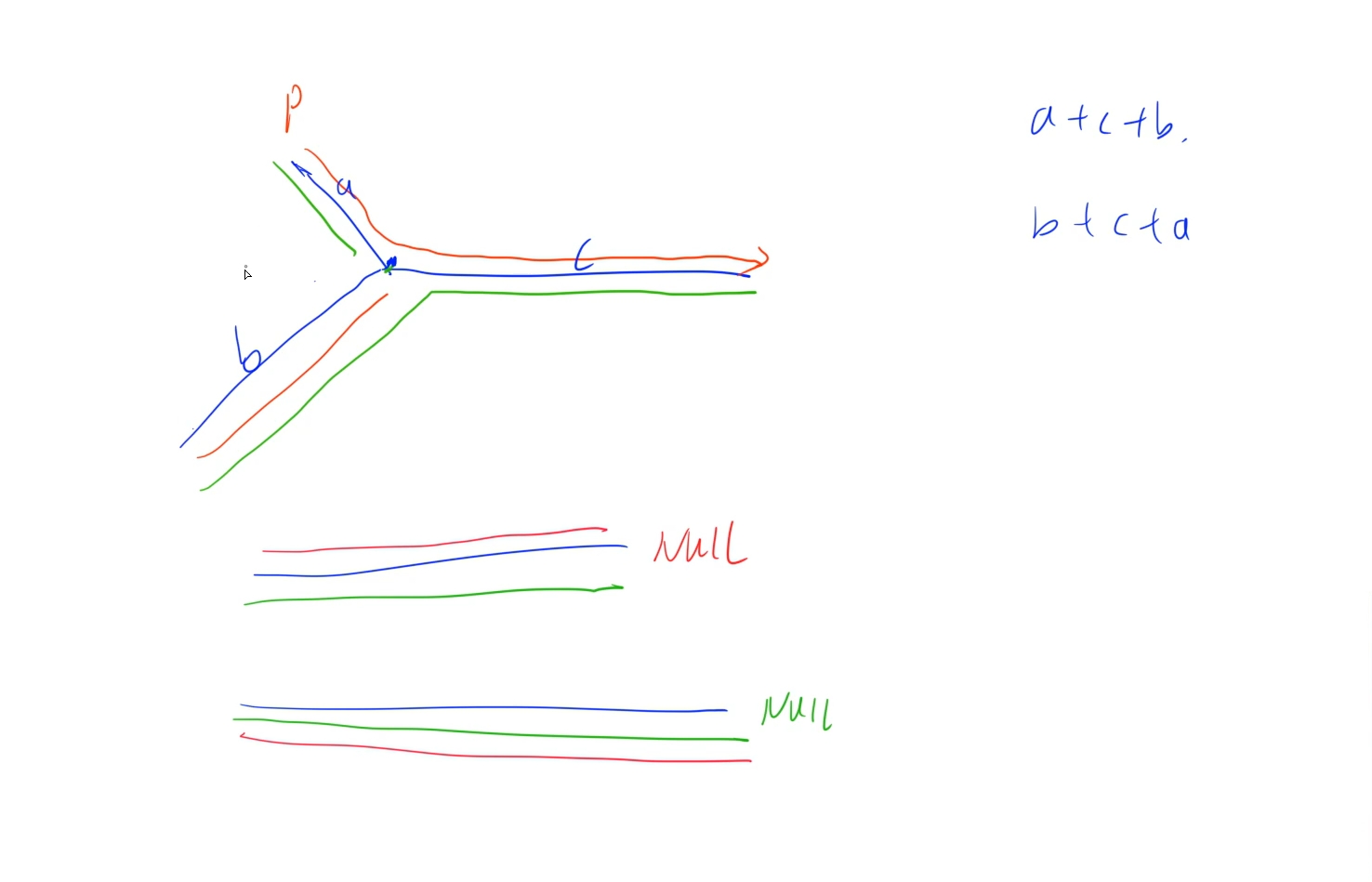
时间复杂度:O(m + n)
注释代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {auto p = headA, q = headB;while(p != q){p = p ? p -> next: headB; //p是否为空,不为空则往后走,为空则往链表B走q = q ? q -> next: headA; //q是否为空,不为空则往后走,为空则往链表A走}return p; //返回p或者q}
};
纯享版:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {auto p = headA, q = headB;while(p != q){p = p ? p -> next : headB;q = q ? q -> next : headA;}return q;}
};
LeetCode162.寻找峰值:
题目描述:
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000
-2^31 <= nums[i] <= 2^31 - 1
对于所有有效的 i 都有 nums[i] != nums[i + 1]
思路:
首先先观察找到规律,发现从左边开始看,一旦往后走出现减小了就会出现峰值,因为nums[-1]是负无穷的,只要后面元素减小就会出现峰值,但是由于题目要求时间复杂度是O(logn),那么想起老朋友二分,借鉴前面发现的规律,从中间点mid开始看,如果mid+1的数是大于mid的值的,那么右边一定存在峰值,于是将区间转移到右半段,以此二分

时间复杂度:O(logn)
代码:
class Solution {
public:int findPeakElement(vector<int>& nums) {int l = 0, r = nums.size() -1 ;while(l < r){int mid = l + r >> 1;if(nums[mid] > nums[mid + 1]) r = mid;else l = mid + 1;}return r;}
};
LeetCode164.最大间距:
题目描述:
给定一个无序的数组 nums,返回 数组在排序之后,相邻元素之间最大的差值 。如果数组元素个数小于 2,则返回 0 。
您必须编写一个在「线性时间」内运行并使用「线性额外空间」的算法。
示例 1:
输入: nums = [3,6,9,1]
输出: 3
解释: 排序后的数组是 [1,3,6,9], 其中相邻元素 (3,6) 和 (6,9) 之间都存在最大差值 3。
示例 2:
输入: nums = [10]
输出: 0
解释: 数组元素个数小于 2,因此返回 0。
提示:
1 <= nums.length <= 10^5
0 <= nums[i] <= 10^9
思路:
首先梳理题意: 给出乱序数组,需要你求出排序之后的数组相邻两个元素之间的最大差值,但是要使用线性的时间和空间复杂度(不能直接sort)
这里使用桶排序:

时间复杂度:
根据题意要求,时间和空间都是O(n)的
注释代码:
class Solution {
public:int maximumGap(vector<int>& nums) {struct Range{ //定义区间int min, max;bool used;Range() : min(INT_MAX), max(INT_MIN), used(false){}};int n = nums.size();int Min = INT_MAX, Max = INT_MIN;for(auto x : nums) //找到nums中的最大值和最小值{Min = min(Min, x); Max = max(Max, x);}if(n < 2 || Min == Max) return 0; //只有一个数或者数值都是一致的,那么间距为0vector<Range> r(n - 1); //定义n-1个区间间隔int len = (Max - Min + n - 2) / (n -1); //区间长度for(auto x : nums) //判断每个元素属于哪个区间{if(x == Min) continue; //Min不属于任何区间int k = (x - Min - 1) / len; //判断当前数组元素属于哪个区间, 当前数 / len: 每个区间放len个数r[k].used = true; //标记一下当前属于区间被用过r[k].min = min(r[k].min, x); //记录当前区间的最小值r[k].max = max(r[k].max, x); //记录当前区间的最大值}int res = 0;for(int i = 0, last = Min; i < n - 1; i++) //比较每个区间{if(r[i].used){res = max(res, r[i].min - last); //最大间距为当前区间的最小值和上个区间的最大值last = r[i].max; //将last更新为当前区间的最大值}}return res;}
};纯享版:
class Solution {
public:int maximumGap(vector<int>& nums) {struct Range{int min, max;bool used;Range() : max(INT_MIN), min(INT_MAX), used(false){}};int n = nums.size();int Max = INT_MIN, Min = INT_MAX;for(auto x : nums){Max = max(Max, x);Min= min(Min, x);}if(n < 2 || Max == Min) return 0;vector<Range> r(n - 1);int len = (Max - Min + n - 2) / (n - 1);for(auto x : nums){if(x == Min) continue;int k = (x - Min - 1) / len;r[k].used = true;r[k].min = min(r[k].min, x);r[k].max = max(r[k].max, x);}int res = 0;for(int i = 0, last = Min; i < n -1; i++){if(r[i].used){res = max(res, r[i].min - last);last = r[i].max;}}return res;}
};LeetCode165.比较版本号:
题目描述:
给你两个 版本号字符串 version1 和 version2 ,请你比较它们。版本号由被点 ‘.’ 分开的修订号组成。修订号的值 是它 转换为整数 并忽略前导零。
比较版本号时,请按 从左到右的顺序 依次比较它们的修订号。如果其中一个版本字符串的修订号较少,则将缺失的修订号视为 0。
返回规则如下:
如果 version1 < version2 返回 -1,
如果 version1 > version2 返回 1,
除此之外返回 0。
示例 1:
输入:version1 = “1.2”, version2 = “1.10”
输出:-1
解释:
version1 的第二个修订号为 “2”,version2 的第二个修订号为 “10”:2 < 10,所以 version1 < version2。
示例 2:
输入:version1 = “1.01”, version2 = “1.001”
输出:0
解释:
忽略前导零,“01” 和 “001” 都代表相同的整数 “1”。
示例 3:
输入:version1 = “1.0”, version2 = “1.0.0.0”
输出:0
解释:
version1 有更少的修订号,每个缺失的修订号按 “0” 处理。
提示:
1 <= version1.length, version2.length <= 500
version1 和 version2 仅包含数字和 ‘.’
version1 和 version2 都是 有效版本号
version1 和 version2 的所有修订号都可以存储在 32 位整数 中
思路:
将’.'中间的数字从左往右依次提取出来,依次对比,比如1.001 和1.0000001: 1后面的 001 和00000001转成整数之后都是1,同时,如果出现长度不足的情况,则末尾补零,比如1.0 和 1.0. 0.0 : 1.0后面不足直接默认为0
时间复杂度:O(max(n, m))
注释代码:
class Solution {
public:int compareVersion(string v1, string v2 ) {for(int i = 0, j= 0; i < v1.size() || j < v2.size();){int a = i, b = j;while(a < v1.size() && v1[a] != '.') a++; //找到.之前的数while(b < v2.size() && v2[b] != '.') b++; //从i ~ a - i: 第a位不算,所以长度为 a - 1 - i + 1 = a - iint x = a == i ? 0 : stoi(v1.substr(i, a - i)); //如果a== i说明a == v1.size,则只能为0, 否则就将当前位数字字符转成整数数字方便比较int y = b == j ? 0 : stoi(v2.substr(j, b - j));if(x > y) return 1; //如果v1的当前位大于v2的当前位,那么返回1if(x < y) return -1;i = a + 1, j = b + 1; //i和j处都是'.',下一个数字从a+ 1和b+ 1开始}return 0;}
};纯享版:
class Solution {
public:int compareVersion(string v1, string v2) {for(int i = 0, j = 0; i < v1.size() || j < v2.size();){int a = i, b = j;while(a < v1.size() && v1[a] != '.') a++;while(b < v2.size() && v2[b] != '.') b++;int x = a == i ? 0 : stoi(v1.substr(i, a - i));int y = b == j ? 0 : stoi(v2.substr(j, b - j));if(x > y) return 1;if(x < y) return -1;i = a + 1, j = b + 1;}return 0;}
};
LeetCode166.分数到小数:
题目描述:
给定两个整数,分别表示分数的分子 numerator 和分母 denominator,以 字符串形式返回小数 。
如果小数部分为循环小数,则将循环的部分括在括号内。
如果存在多个答案,只需返回 任意一个 。
对于所有给定的输入,保证 答案字符串的长度小于 10^4 。
示例 1:
输入:numerator = 1, denominator = 2
输出:“0.5”
示例 2:
输入:numerator = 2, denominator = 1
输出:“2”
示例 3:
输入:numerator = 4, denominator = 333
输出:“0.(012)”
提示:
-2^31 <= numerator, denominator <= 2^31 - 1
denominator != 0
思路:
总体是高精度除法,但是细节很多,比如循环部分怎么判断: 通过判断余数是否已经出现过,因为余数一旦相同,那么之后的部分只会按照上个相同余数之后的部分相同的循环下去,怎么判断余数是否出现过同时又能找到余数出现的位置呢? 使用hash表,存储出现余数时商的位数,在后面遇到相同余数时只要将该余数之后的全部商截取下来放到循环部分()就是最后一直会循环的商
时间复杂度:
假设分母大小为n,那么余数为0~n-1,最多循环n次,在n+ 1次时必有相同余数,所以总的时间复杂度为O(n)
注释代码:
class Solution {
public:string fractionToDecimal(int numerator, int denominator) {typedef long long LL;LL x = numerator, y = denominator;if(x % y == 0) return to_string(x / y); //如果可以整除则直接返回整除的结果string res;if((x < 0) ^ (y < 0)) res += '-'; //x小于0或者y小于0,则最终结果是一个负数,需要加上负号x = abs(x), y = abs(y); //同时对x和y取绝对值res += to_string(x / y) + '.', x %= y; //先算整数部分,这里的x是余下的数unordered_map<LL, int> hash;while(x){hash[x] = res.size(); //记录余数为x的位置x *= 10; //余数乘10res += to_string(x / y); //将商加入答案串x %= y; //计算余下的余数if(hash.count(x)) //判断是否已经出现过{//出现过的余数开始的商则是循环部分res = res.substr(0, hash[x]) + '(' + res.substr(hash[x]) + ')';break;}}return res;}
};纯享版:
class Solution {
public:string fractionToDecimal(int numerator, int denominator) {typedef long long LL;LL x = numerator, y = denominator;if(x % y == 0) return to_string(x / y);string res;if((x < 0) ^ (y < 0)) res += '-';x = abs(x), y = abs(y);res += to_string(x / y) + '.', x = x % y;unordered_map<LL, int> hash;while(x){hash[x] = res.size();x *= 10;res += to_string(x / y);x %= y;if(hash.count(x)){res = res.substr(0, hash[x]) + '(' + res.substr(hash[x]) + ')';break;}}return res;}
};LeetCode167.两数之和Ⅱ-输入有序数组:
题目描述:
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]
解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
提示:
2 <= numbers.length <= 3 * 10^4
-1000 <= numbers[i] <= 1000
numbers 按 非递减顺序 排列
-1000 <= target <= 1000
仅存在一个有效答案
思路:
正常暴力做法就是使用双层循环看当前数和另外一个数的和是否等于target,这样做的时间复杂度是O(n*n)的,所以考虑使用双指针算法进行优化,双指针要求具有单调性, 可以发现当我们的i从前面往后遍历时,因为数组是非递减的,为了满足target,j只能不断往前移动,因此可以使用双指针算法进行优化
时间复杂度:O(n)
代码:
class Solution {
public:vector<int> twoSum(vector<int>& numbers, int target) {for(int i = 0, j = numbers.size() - 1; i < j; i++){while(i < j && numbers[i] + numbers[j] > target) j--;if(i < j && numbers[i] + numbers[j] == target) return{i + 1, j + 1};}return {};}
};
LeetCode168.Excel表列名称:
题目描述:
给你一个整数 columnNumber ,返回它在 Excel 表中相对应的列名称。
例如:
A -> 1
B -> 2
C -> 3
…
Z -> 26
AA -> 27
AB -> 28
…
示例 1:
输入:columnNumber = 1
输出:“A”
示例 2:
输入:columnNumber = 28
输出:“AB”
示例 3:
输入:columnNumber = 701
输出:“ZY”
示例 4:
输入:columnNumber = 2147483647
输出:“FXSHRXW”
提示:
1 <= columnNumber <= 2^31 - 1
思路:

时间复杂度:O(n)
注释代码:
class Solution {
public:string convertToTitle(int n) {string res;int k = 1;for(long long p = 26; p < n; p *= 26){n -= 26; //当前位数的第几位k++; //先确定位数}n--;while(k--){res += n % 26 + 'A';n /= 26;}reverse(res.begin(), res.end());return res;}
};
纯享版:
class Solution {
public:string convertToTitle(int n) {string res;while(n > 0){n--;res += n%26 + 'A'; //先取个位n /= 26; //求下一位个位的剩余数}reverse(res.begin(), res.end());return res;}
};LeetCode169.多数元素:
题目描述:
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
提示:
n == nums.length
1 <= n <= 5 * 10^4
-10^9 <= nums[i] <= 10^9
进阶:尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
思路:
根据题意,要找出出现次数大于向下取整的n/2的数,通过简单尝试几个n可以发现,要找的数大于其他所有数的个数总和,于是我们可以利用这个特性,使用“消消乐”的方式将要找的数跟其他所有数进行抵消,最后剩下的一定是要找的数-》维护两个值: 一个是当前保存的数, 一个是保存数的个数,枚举数组每一个元素,只要跟当前数不一致则将个数减1,反之加1,如果个数减为0则将当前枚举的数保存下来继续比对,最后通过抵消,会将数量大于其他元素个数之和的数留下来
时间复杂度:
每个元素遍历一次,时间复杂度为O(n),而且只用了两个常量空间进行存储,空间复杂度是O(n)的
注释代码:
class Solution {
public:int majorityElement(vector<int>& nums) {int r = 0, c = 0;for(int i = 0; i < nums.size(); i++){if(!c) r = nums[i], c = 1; //如果当前维护的数被抵消完了,就将当前位置的数存下来,当前数的个数为1else if(r == nums[i]) c++; //否则c!=0,则表示当前维护的数还有,如果当前位置的数等于维护的数,则个数+1else c--; //否则就用当前维护的数抵消当前位置上的数,个数-1}return r;}
};
纯享版:
class Solution {
public:int majorityElement(vector<int>& nums) {int number = 0, cnt = 0;for(auto x : nums){if(!cnt) number = x, cnt = 1;else if(x == number) cnt++;else cnt --;}return number;}
};
LeetCode171.Excel表列序号:
题目描述:
给你一个字符串 columnTitle ,表示 Excel 表格中的列名称。返回 该列名称对应的列序号 。
例如:
A -> 1
B -> 2
C -> 3
…
Z -> 26
AA -> 27
AB -> 28
…
示例 1:
输入: columnTitle = “A”
输出: 1
示例 2:
输入: columnTitle = “AB”
输出: 28
示例 3:
输入: columnTitle = “ZY”
输出: 701
提示:
1 <= columnTitle.length <= 7
columnTitle 仅由大写英文组成
columnTitle 在范围 [“A”, “FXSHRXW”] 内
思路:看成26进制的数进行进制转换
时间复杂度:O(n)
注释代码:
class Solution {
public:int titleToNumber(string columnTitle) {long long res = 0;for(int i = 0; i < columnTitle.size(); i++){res = res * 26 + columnTitle[i] - 'A' + 1;}return res;}
};
数位:
class Solution {
public:int titleToNumber(string s) {int a = 0;for(long long i = 0, p = 26; i < s.size() - 1; i++, p *= 26){a += p; }int b = 0;for(auto c : s) b = b * 26 + c - 'A';return a + b + 1;}
};LeetCode172.阶乘后的零:
题目描述:
给定一个整数 n ,返回 n! 结果中尾随零的数量。
提示 n! = n * (n - 1) * (n - 2) * … * 3 * 2 * 1
示例 1:
输入:n = 3
输出:0
解释:3! = 6 ,不含尾随 0
示例 2:
输入:n = 5
输出:1
解释:5! = 120 ,有一个尾随 0
示例 3:
输入:n = 0
输出:0
提示:
0 <= n <= 10^4
进阶:你可以设计并实现对数时间复杂度的算法来解决此问题吗?
思路:
首先读取题意并进行分解: 阶乘后的零, 零是怎么产生的-> 10: 10 = 2 * 5,也就是说只要找到阶乘中2 和5被乘的次数中二者的最小值就是0的个数, 如何找到阶乘中2^a 和5^b中的a和b,那么现在的问题是解决如何在阶乘(1 ~n)中找到 2出现的次数: 首先1 ~ n中2可能出现的形式为2,2^2, 2^3,…,
统计1 ~n中:
1.P的倍数个数: n/p下取整
2.p2的倍数个数:n/p2下取整
…
k.p^k的倍数个数: n/p^k下取整
如果1n中的某个数x有k个p,那么x会在1中算一次,2中算一次。。总共统计k次,那么对于1n中任意一个数,含有的p都会被计算出来,那么总共的统计个数就是p出现的次数
最后又因为2的次数肯定比5的出现的次数多,所以,我们只需要求出5在n的阶乘中出现的次数,就是阶乘后的零的个数
时间复杂度:O(logn)底为5
代码:
class Solution {
public:int trailingZeroes(int n) {int res = 0;while(n > 0) res += n / 5, n /= 5; return res;}
};
LeetCode173.二叉搜索树迭代器:
题目描述:
实现一个二叉搜索树迭代器类BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器:
BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。
boolean hasNext() 如果向指针右侧遍历存在数字,则返回 true ;否则返回 false 。
int next()将指针向右移动,然后返回指针处的数字。
注意,指针初始化为一个不存在于 BST 中的数字,所以对 next() 的首次调用将返回 BST 中的最小元素。
你可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 的中序遍历中至少存在一个下一个数字。
示例:
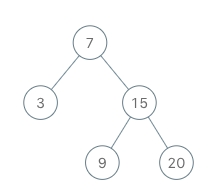
输入
[“BSTIterator”, “next”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]
解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // 返回 3
bSTIterator.next(); // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 20
bSTIterator.hasNext(); // 返回 False
提示:
树中节点的数目在范围 [1, 10^5] 内
0 <= Node.val <= 10^6
最多调用 10^5 次 hasNext 和 next 操作
进阶:
你可以设计一个满足下述条件的解决方案吗?next() 和 hasNext() 操作均摊时间复杂度为 O(1) ,并使用 O(h) 内存。其中 h 是树的高度。
思路:
迭代器就是将原本的中序遍历代码拆分出来,而next函数是每次调用能返回当前指针的值以及将当前指针按中序遍历顺序移动,hasNext是判断是否遍历完,因为按照中序遍历,直到全部遍历完,指针才无法继续往下移动。
时间复杂度:
O(1), 空间复杂度O(h)
注释代码:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class BSTIterator {
public:stack<TreeNode*> stk;BSTIterator(TreeNode* root) {while(root) //将左链全部加入栈中{stk.push(root);root = root -> left;}}int next() { //获取当前节点的值,但是在下次再获取时需要按照中序遍历的顺序走auto root = stk.top();stk.pop();int val = root -> val;root = root -> right;while(root){stk.push(root);root = root -> left;}return val;}bool hasNext() { //返回栈是否为空,如果为空则说明没有元素了,指针无法向右移动,中序遍历完了return stk.size();}
};/*** Your BSTIterator object will be instantiated and called as such:* BSTIterator* obj = new BSTIterator(root);* int param_1 = obj->next();* bool param_2 = obj->hasNext();*/
纯享版:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class BSTIterator {
public:stack<TreeNode*> stk;BSTIterator(TreeNode* root) {while(root){stk.push(root);root = root -> left;}}int next() {auto root = stk.top();stk.pop();int val = root -> val;root = root -> right;while(root){stk.push(root);root = root -> left;}return val;}bool hasNext() {return stk.size();}
};/*** Your BSTIterator object will be instantiated and called as such:* BSTIterator* obj = new BSTIterator(root);* int param_1 = obj->next();* bool param_2 = obj->hasNext();*/LeetCode174.地下城游戏:
题目描述:
恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
示例 1:
输入:dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出:7
解释:如果骑士遵循最佳路径:右 -> 右 -> 下 -> 下 ,则骑士的初始健康点数至少为 7 。
示例 2:
输入:dungeon = [[0]]
输出:1
提示:
m == dungeon.length
n == dungeon[i].length
1 <= m, n <= 200
-1000 <= dungeon[i][j] <= 1000
思路:
动态规划问题:
题意需要求从起点走到终点需要的最低血量,那么设定集合:f[i][j]表示从(i, j)走到终点所需要的血量最小值,根据闫氏DP分析法:划分集合看最后一步是往右还是往下走
1.往右走f[i][j + 1]: 假设当前格子所需要的最低血量为x,那么在加上当前格子w[i][j]之后,剩余血量需要大于等于f[i][j + 1]也就是下一步格子能走到终点的最低血量: f[i][j] + w[i][j] >= f[i][j + 1] -> f[i][j] = f[i][j + 1] - w[i][j]
2.往下走f[i + 1][j]: 假设当前格子所需要的最低血量为x,那么在加上当前格子w[i][j]之后,剩余血量需要大于等于f[i + 1][j]也就是下一步格子能走到终点的最低血量: f[i][j] + w[i][j] >= f[i + 1][j] -> f[i][j] = f[i + 1][j] - w[i][j]
由上述分析可知正向Dp是无法求出状态矩阵的,所以需要反向Dp,从后往前推。
需要注意的是边界条件:
首先从终点处往前推,终点的状态很重要:终点最理想的状态就是刚好剩余1血量救下公主,那么f[n-1][m-1]为1 - w[i][j]:x - w[i][j] = 1,简单的交换律,当然如果最后一个格子是回血的,那么只需要1血量就能救下公主,所以f[n-1][m-1]= max(1, 1 - w[i][j])
时间复杂度:O(mn)
注释代码:
class Solution {
public:int calculateMinimumHP(vector<vector<int>>& w) {int n = w.size(), m = w[0].size();vector<vector<int>> f(n, vector<int>(m, 1e8));for(int i = n - 1; i >= 0; i--){for(int j = m - 1; j >= 0; j--){//到终点时,血量最好刚好为1,如果是加血量则直接最小值为1,如果是减血量,则最小值需要减去血量刚好剩余为1if(i == n - 1 && j == m - 1) f[i][j] = max(1, 1 - w[i][j]);else{if(i + 1 < n) f[i][j] = f[i + 1][j] - w[i][j];if(j + 1 < m) f[i][j] = min(f[i][j], f[i][j + 1] - w[i][j]);//判断从当前格子往终点走的血量最低不能低于1f[i][j] = max(1, f[i][j]);}}}return f[0][0]; //返回从起点到终点需要的最低血量}
};纯享版:
class Solution {
public:int calculateMinimumHP(vector<vector<int>>& w) {int n = w.size(), m = w[0].size();vector<vector<int>> f(n, vector<int>(m, 1e8));for(int i = n - 1; i >= 0; i--){for(int j = m - 1; j >= 0; j--){if(i == n - 1 && j == m - 1) f[i][j] = max(1, 1 - w[i][j]);if(i + 1 < n) f[i][j] = f[i + 1][j] - w[i][j];if(j + 1 < m) f[i][j] = min(f[i][j], f[i][j + 1] - w[i][j]);f[i][j] = max(1, f[i][j]);}}return f[0][0];}
};
LeetCode179.最大数:
题目描述:
给定一组非负整数 nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。
注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。
示例 1:
输入:nums = [10,2]
输出:“210”
示例 2:
输入:nums = [3,30,34,5,9]
输出:“9534330”
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 10^9
思路:
题意是需要将nums中的每个元素拼起来达到数值上的最大
对于其中两个元素a和b来说,如果ab比ba大,那么肯定先将a放b的前面,受此启发,如果我们能将所有元素按拼成之后的结果来排序,拼凑的时候将放在前面会变大的元素放到前面,这样最终的结果就会取得最大值,比如: 34, 5, 9 : 首先是34 和5 ,当然是5放前面较大,于是排序一下: 5, 34, 9: 然后看34 和9 ,明显是9放前面较大,于是: 5, 9, 34, 然后再看5和9,肯定是9放前面较大,所以: 9, 5, 34,明显的最终结果9534也是其中拼成之后最大的

如果将其按照我们的设想来排序:重新定义sort的比较机制,将x和y的比较定义成它们转成字符串之后按字典序来比较,也就是string(xy) > string(yx): 按照降序来逐个排序并重构nums中的元素
最后从前往后将nums元素逐个拼接起来去除前导零即可
时间复杂度:

注释代码:
class Solution {
public:string largestNumber(vector<int>& nums) {//重新定义比较符号sort(nums.begin(), nums.end(), [](int x, int y) {string a = to_string(x), b = to_string(y); //将int转成string类型return a + b > b + a; //定义 ab > ba,按照拼在一起之后字典序的降序进行重新sort});string res;for(auto x : nums) res += to_string(x); //将降序排好的数组拼在一起int k = 0;while(k + 1 < res.size() && res[k] == '0') k++; //去除前导0return res.substr(k);}
};纯享版:
class Solution {
public:string largestNumber(vector<int>& nums) {sort(nums.begin(), nums.end(), [](int x, int y){string a = to_string(x), b = to_string(y);return a + b > b + a;});string res;for(auto x : nums) res += to_string(x);int k = 0; while(k + 1 < res.size() && res[k] == '0') k++;return res.substr(k);}
};LeetCode187.重复的DNA序列:
题目描述:
DNA序列 由一系列核苷酸组成,缩写为 ‘A’, ‘C’, ‘G’ 和 ‘T’.。
例如,“ACGAATTCCG” 是一个 DNA序列 。
在研究 DNA 时,识别 DNA 中的重复序列非常有用。
给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA 分子中出现不止一次的 长度为 10 的序列(子字符串)。你可以按 任意顺序 返回答案。
示例 1:
输入:s = “AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT”
输出:[“AAAAACCCCC”,“CCCCCAAAAA”]
示例 2:
输入:s = “AAAAAAAAAAAAA”
输出:[“AAAAAAAAAA”]
提示:
0 <= s.length <= 10^5
s[i]==‘A’、‘C’、‘G’ or ‘T’
思路:
题意:长度为10的字符串中,如果重复出现则输出该字符串
将所有长度为10的字符串截取出来放入hash表中, 如果重复出现,则次数超过1次,直接输出即可
时间复杂度:O(n)
注释代码:
class Solution {
public:vector<string> findRepeatedDnaSequences(string s) {unordered_map<string, int> hash;for(int i = 0; i + 10 <= s.size(); i++) //截取任意长度为10的字符串存入hash表{hash[s.substr(i, 10)]++;}vector<string> res;for(auto [s, c] : hash) //查hash表中每个字符串,如果有超过2的则为答案{if(c > 1) res.push_back(s);}return res;}
};
纯享版:
class Solution {
public:vector<string> findRepeatedDnaSequences(string s) {unordered_map<string, int> hash;for(int i = 0; i + 10 <= s.size(); i++){hash[s.substr(i, 10)]++;}vector<string> res;for(auto [s, c] : hash){if(c > 1) res.push_back(s);}return res;}
};
LeetCode188.买卖股票的最佳时机Ⅳ:
题目描述:
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1]
输出:2
解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3]
输出:7
解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
提示:
1 <= k <= 100
1 <= prices.length <= 1000
0 <= prices[i] <= 1000
思路:
题意就是让你规划最多k次不重叠的交易,使得交易获得的收益最大。
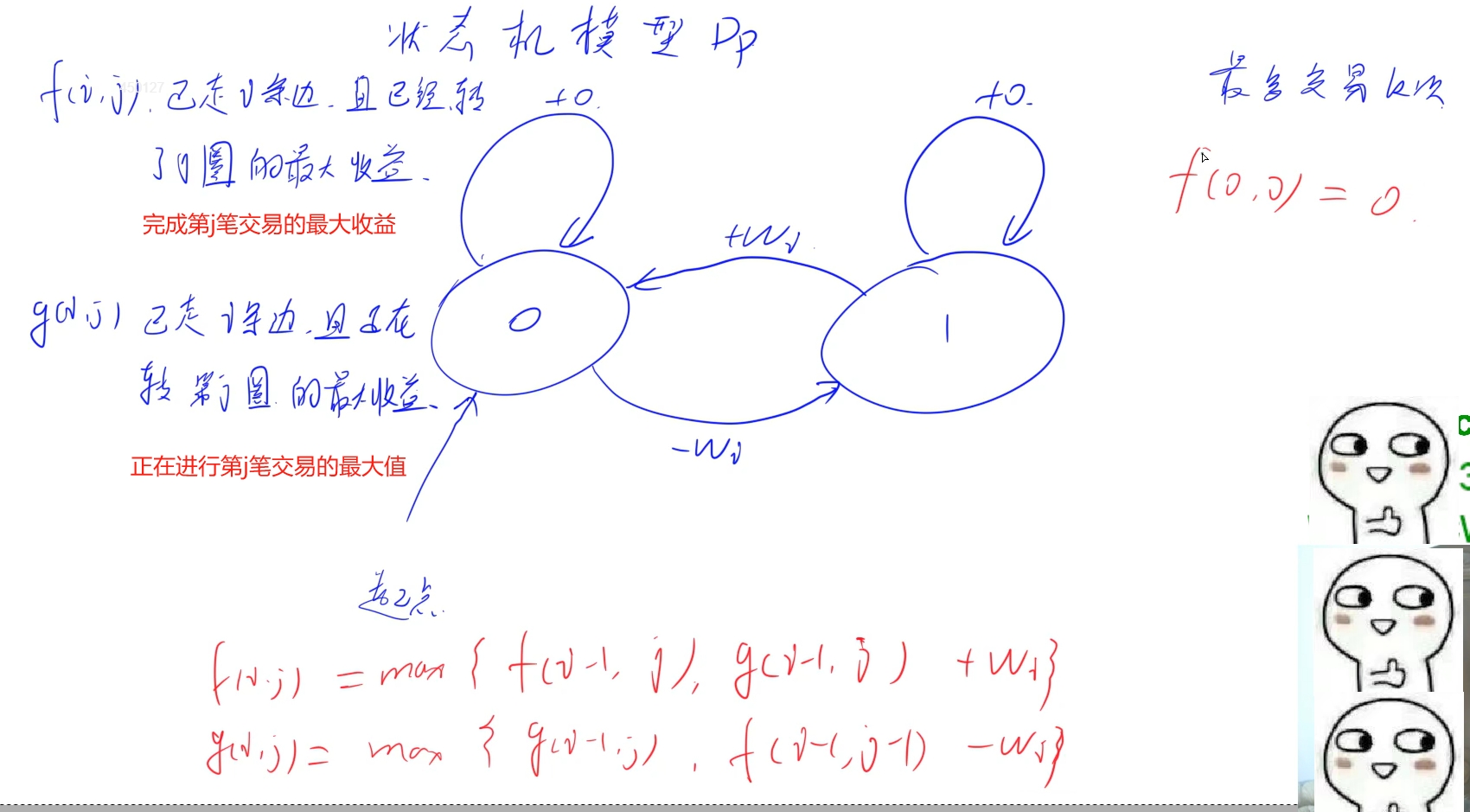
状态机模型Dp:如图所示,将手上持有股票(买入)和未持有股票(卖出)看成两种状态,首先起点肯定是进入到未持有股票状态,然后可以选择不买入,那收益就保持不变,如果买入则需要花费第i支股票的金额w[i], 买入之后变成持有股票状态,也可以选择不卖出,那么收益还是保持不变,如果卖出就可以获得卖出当前第i支股票的收益
使用f[i][j]表示在第i天时,已经完成第j笔交易所获得的最大收益,他的状态由
1.上一次未买入时的最大收益也就是f[i - 1][j]
2.上一次买入当前第i天的股票时的最大收益加上卖出当前第i天的股票的金额w[i]: g[i - 1][j] + w[i]共同决定
f[i][j] = max(f[i - 1][j], g[i - 1][j] - w[i])
使用g[i][j]表示在第i天时,正在进行第j笔交易时的最大收益,他的状态由
1.上一天并未卖出当前第i天的股票的最大收益g[i - 1][j]
2.上一笔交易已经完成,也就是手上没有持有股票,并且当前准备买入当前第i天的股票并进行第j次交易的最大收益:f[i - 1][j - 1] - w[i]
g[i][j] = max(g[i - 1][j], f[i - 1][j - 1] - w[i])
时间复杂度:
注释代码:
class Solution {
public:int maxProfit(int k, vector<int>& prices) {const int INF = 1e8;int n = prices.size();int res = 0;if(k > n / 2) {for(int i = 0; i + 1 < n; i++){if(prices[i + 1] > prices[i]) res += prices[i + 1] - prices[i];}return res;}vector<vector<int>> f(n + 1, vector<int>(k + 1, -INF));auto g = f;f[0][0] = 0;for(int i = 1; i <= n; i++){for(int j = 0; j <= k; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] + prices[i - 1]);g[i][j] = g[i - 1][j];if(j) g[i][j] = max(g[i][j], f[i - 1][j - 1] - prices[i - 1]);res = max(res, f[i][j]);}}return res;}
};
优化版(滚动数组):
class Solution {
public:int maxProfit(int k, vector<int>& prices) {const int INF = 1e8;int n = prices.size();int res = 0;if(k > n / 2) {for(int i = 0; i + 1 < n; i++){if(prices[i + 1] > prices[i]) res += prices[i + 1] - prices[i];}return res;}vector<vector<int>> f(2, vector<int>(k + 1, -INF));auto g = f;f[0][0] = 0;for(int i = 1; i <= n; i++){for(int j = 0; j <= k; j++){f[i & 1][j] = max(f[i - 1 & 1][j], g[i - 1 & 1][j] + prices[i - 1]);g[i & 1][j] = g[i - 1 & 1][j];if(j) g[i & 1][j] = max(g[i & 1][j], f[i - 1 & 1][j - 1] - prices[i - 1]);res = max(res, f[i & 1][j]);}}return res;}
};