当前位置：首页 > news >正文

《算法导论》第 18 章 - B 树

news 2025/8/12 9:39:14

引言

在数据库和文件系统中，我们经常需要高效地管理大量数据，这些数据通常存储在磁盘等外存设备中。B 树作为一种平衡的多路搜索树，因其优异的外存性能而被广泛应用。它能够有效减少磁盘 I/O 操作，提高数据检索、插入和删除的效率。本文将基于《算法导论》第 18 章，详细讲解 B 树的定义、基本操作（查找、插入、删除），并提供完整的 C++ 实现代码，帮助大家深入理解 B 树的工作原理。

18.1 B 树的定义

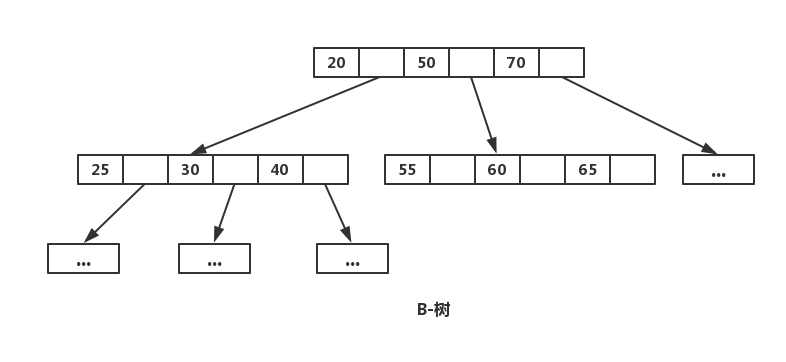
18.1.1 什么是 B 树？

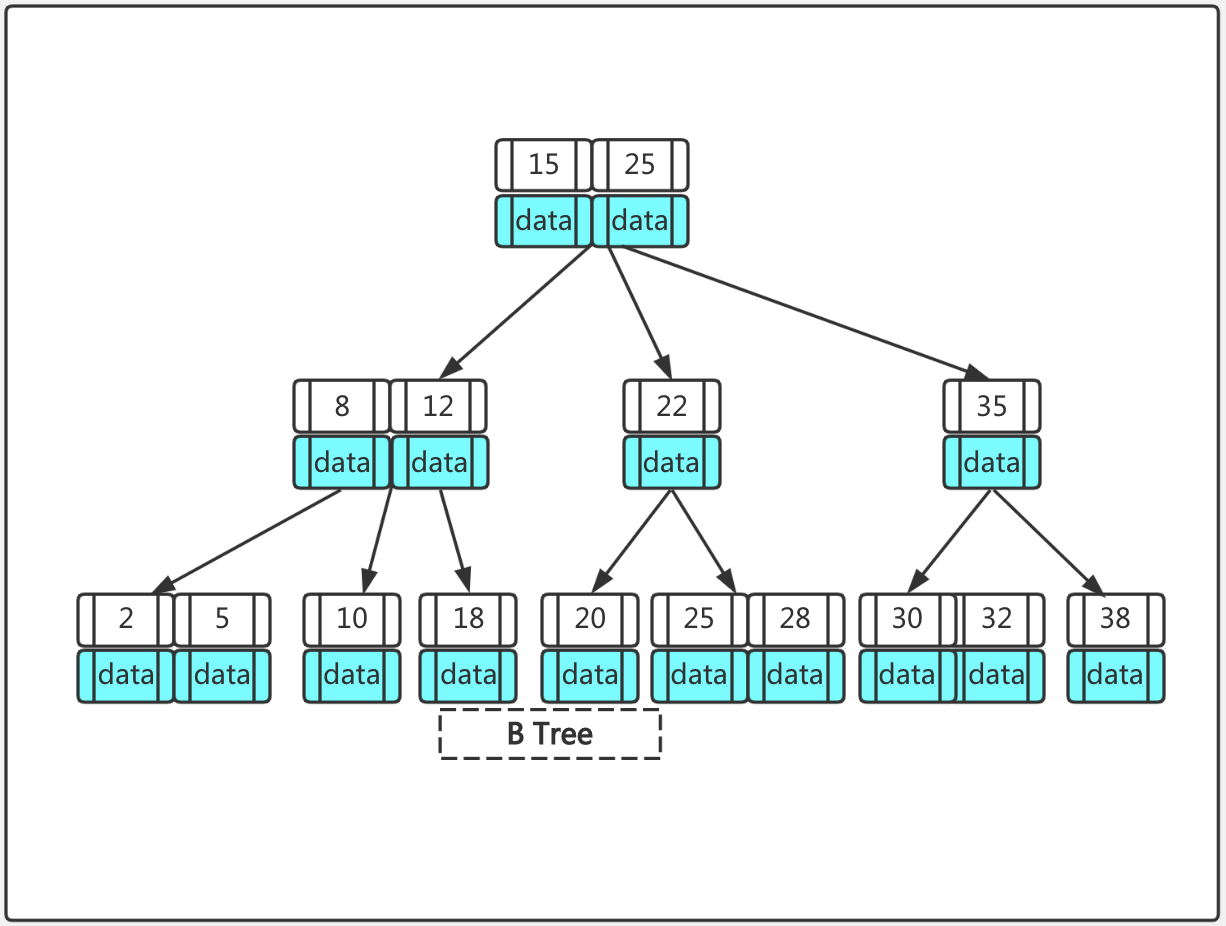
B 树是一种多路平衡查找树，它的每个节点可以存储多个关键字，并且通过平衡结构保证了高效的查找、插入和删除操作。B 树的 "平衡" 体现在所有叶子节点位于同一层，避免了像普通二叉搜索树那样可能出现的极端倾斜情况。

18.1.2 B 树的正式定义（m 阶 B 树）

一棵m 阶 B 树是满足以下性质的树：

每个节点最多有 m 个孩子（即节点的度≤m）。
除根节点外，每个非叶子节点至少有⌈m/2⌉个孩子（即度≥⌈m/2⌉）。
根节点至少有 2 个孩子（除非根节点是叶子节点）。
所有叶子节点都在同一层，且不包含任何信息（或被视为外部节点）。
每个非叶子节点包含若干关键字，关键字按升序排列。若一个节点有 k 个孩子，则它包含 k-1 个关键字，且每个关键字对应一个子树的分隔符。

例如，一个 3 阶 B 树（m=3）的非叶子节点最多有 3 个孩子、2 个关键字；除根外的非叶子节点至少有 2 个孩子、1 个关键字。

18.2 B 树上的基本操作

18.2.1 B 树的节点结构

首先定义 B 树节点的结构体，包含关键字数组、孩子指针数组和当前关键字数量：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;template <typename T>
struct BTreeNode {vector<T> keys;               // 关键字数组vector<BTreeNode<T>*> children; // 孩子指针数组BTreeNode<T>* parent;         // 父节点指针int keyCount;                 // 当前关键字数量// 构造函数：初始化节点，最多容纳(m-1)个关键字，m个孩子BTreeNode(int m, BTreeNode<T>* p = nullptr) : parent(p), keyCount(0) {keys.resize(m - 1);       // 关键字最大数量为m-1children.resize(m, nullptr); // 孩子最大数量为m}
};

18.2.2 B 树类的定义

template <typename T>
class BTree {
private:BTreeNode<T>* root;  // 根节点int order;           // B树的阶数（m）int minKeyCount;     // 最小关键字数：⌈m/2⌉ - 1int maxKeyCount;     // 最大关键字数：m - 1// 辅助函数：分裂节点void splitNode(BTreeNode<T>* parentNode, int childIndex);// 辅助函数：合并节点void mergeNodes(BTreeNode<T>* parentNode, int leftChildIndex);// 辅助函数：查找关键字在节点中的位置int findKeyIndex(BTreeNode<T>* node, const T& key);// 辅助函数：获取前驱关键字T getPredecessor(BTreeNode<T>* node, int index);// 辅助函数：获取后继关键字T getSuccessor(BTreeNode<T>* node, int index);// 辅助函数：从左兄弟借关键字void borrowFromLeft(BTreeNode<T>* parentNode, int rightChildIndex);// 辅助函数：从右兄弟借关键字void borrowFromRight(BTreeNode<T>* parentNode, int leftChildIndex);public:BTree(int m) : order(m), root(nullptr) {maxKeyCount = m - 1;minKeyCount = (m % 2 == 0) ? (m / 2 - 1) : (m / 2); // ⌈m/2⌉ - 1}~BTree() {// 析构函数：递归释放所有节点destroyTree(root);}void destroyTree(BTreeNode<T>* node);bool search(const T& key);               // 查找关键字void insert(const T& key);               // 插入关键字bool remove(const T& key);               // 删除关键字void printTree();                        // 打印B树（层序遍历）
};

18.2.3 查找操作

B 树的查找与二叉搜索树类似，区别在于每个节点需要比较多个关键字：

从根节点开始，比较关键字与目标值
若找到匹配关键字，返回成功
若未找到，根据关键字大小进入对应的子树继续查找
若到达叶子节点仍未找到，返回失败

代码实现：

template <typename T>
bool BTree<T>::search(const T& key) {BTreeNode<T>* current = root;while (current != nullptr) {int i = 0;// 找到第一个大于key的关键字位置while (i < current->keyCount && current->keys[i] < key) {i++;}// 找到匹配的关键字if (i < current->keyCount && current->keys[i] == key) {return true;}// 进入对应的子树继续查找current = current->children[i];}return false; // 未找到
}template <typename T>
int BTree<T>::findKeyIndex(BTreeNode<T>* node, const T& key) {int i = 0;while (i < node->keyCount && node->keys[i] < key) {i++;}return i;
}

18.2.4 插入操作

插入操作需要先找到插入位置，若节点已满则需要分裂节点：

若 B 树为空，创建根节点并插入关键字
否则，查找适合插入的叶子节点
若叶子节点未满，直接插入并保持有序
若叶子节点已满（关键字数 = maxKeyCount），分裂节点：
- 将节点从中间分裂为两个节点
- 中间关键字提升到父节点
- 若父节点也满，则递归分裂

分裂节点代码：

template <typename T>
void BTree<T>::splitNode(BTreeNode<T>* parentNode, int childIndex) {BTreeNode<T>* child = parentNode->children[childIndex];BTreeNode<T>* newNode = new BTreeNode<T>(order, parentNode);int mid = maxKeyCount / 2; // 分裂点（中间关键字的索引）// 复制后半部分关键字到新节点newNode->keyCount = maxKeyCount - mid - 1;for (int i = 0; i < newNode->keyCount; i++) {newNode->keys[i] = child->keys[mid + 1 + i];}// 若不是叶子节点，复制后半部分孩子指针到新节点if (child->children[0] != nullptr) {for (int i = 0; i <= newNode->keyCount; i++) {newNode->children[i] = child->children[mid + 1 + i];if (newNode->children[i] != nullptr) {newNode->children[i]->parent = newNode;}}}// 更新原节点的关键字数量child->keyCount = mid;// 父节点中插入分裂出的中间关键字for (int i = parentNode->keyCount; i > childIndex; i--) {parentNode->keys[i] = parentNode->keys[i - 1];parentNode->children[i + 1] = parentNode->children[i];}parentNode->keys[childIndex] = child->keys[mid];parentNode->children[childIndex + 1] = newNode;parentNode->keyCount++;
}

插入操作代码：

template <typename T>
void BTree<T>::insert(const T& key) {if (root == nullptr) {// 空树：创建根节点root = new BTreeNode<T>(order);root->keys[0] = key;root->keyCount = 1;return;}BTreeNode<T>* current = root;BTreeNode<T>* parent = nullptr;// 查找插入位置（叶子节点）while (current != nullptr) {parent = current;int i = 0;while (i < current->keyCount && current->keys[i] < key) {i++;}// 关键字已存在，直接返回if (i < current->keyCount && current->keys[i] == key) {return;}current = current->children[i];}// 在叶子节点插入关键字current = parent;int i = findKeyIndex(current, key);// 移动关键字为新关键字腾出位置for (int j = current->keyCount; j > i; j--) {current->keys[j] = current->keys[j - 1];}current->keys[i] = key;current->keyCount++;// 若节点已满，需要分裂（从叶子向根递归分裂）while (current->keyCount > maxKeyCount) {if (current->parent == nullptr) {// 根节点分裂：创建新根BTreeNode<T>* newRoot = new BTreeNode<T>(order);root = newRoot;newRoot->children[0] = current;current->parent = newRoot;splitNode(newRoot, 0);current = newRoot;} else {// 非根节点分裂BTreeNode<T>* p = current->parent;int idx = findKeyIndex(p, current->keys[0]); // 找到当前节点在父节点中的索引splitNode(p, idx);current = p;}}
}

18.3 从 B 树中删除关键字

删除操作比插入更复杂，删除后可能导致节点关键字数不足，需要合并节点或借调关键字：

找到待删除关键字所在的节点
若节点是叶子节点：直接删除，若删除后关键字数不足则进行平衡处理
若节点是非叶子节点：用前驱或后继关键字替代待删除关键字，再删除前驱 / 后继
平衡处理：
- 若兄弟节点有多余关键字，借调一个关键字
- 若兄弟节点无多余关键字，合并当前节点与兄弟节点

删除操作流程图：

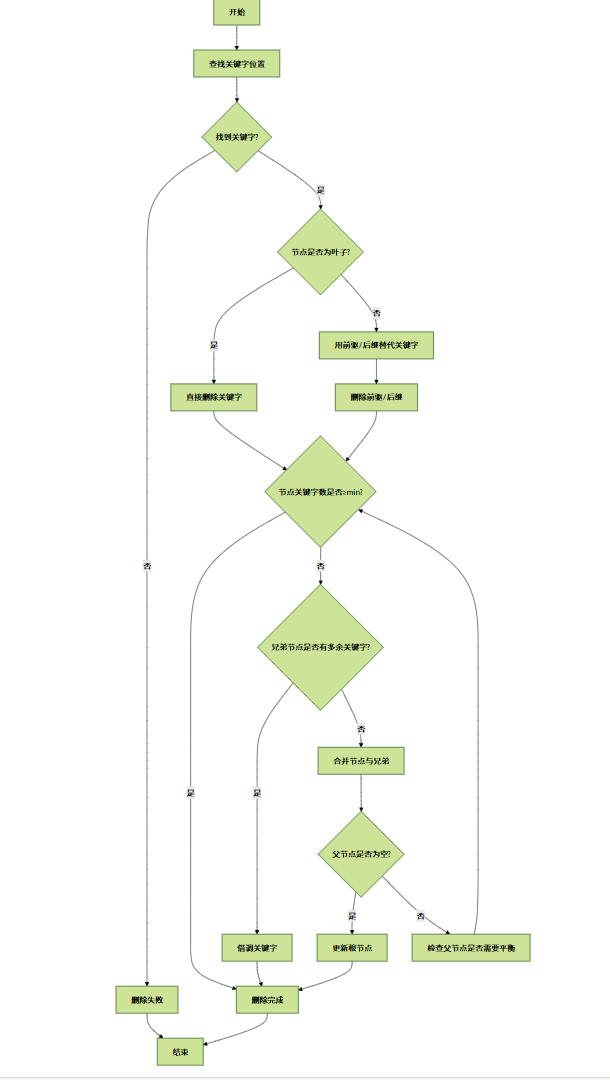
删除操作核心代码：

template <typename T>
bool BTree<T>::remove(const T& key) {if (root == nullptr) return false;BTreeNode<T>* current = root;int i = 0;// 查找关键字所在节点while (current != nullptr) {i = findKeyIndex(current, key);if (i < current->keyCount && current->keys[i] == key) {break; // 找到关键字}current = current->children[i];}if (current == nullptr) return false; // 未找到关键字// 情况1：关键字在叶子节点中if (current->children[0] == nullptr) {// 直接删除for (int j = i; j < current->keyCount - 1; j++) {current->keys[j] = current->keys[j + 1];}current->keyCount--;} else {// 情况2：关键字在非叶子节点中// 找前驱关键字（左子树的最大关键字）T predecessor = getPredecessor(current, i);current->keys[i] = predecessor;// 删除前驱关键字（递归）remove(predecessor);current = root; // 重置current，准备检查平衡if (current == nullptr) return true;}// 平衡处理：若节点关键字数不足while (current->keyCount < minKeyCount) {BTreeNode<T>* parent = current->parent;if (parent == nullptr) {// 根节点关键字数为0时，更新根if (current->keyCount == 0) {root = current->children[0];if (root != nullptr) root->parent = nullptr;delete current;}break;}// 找到当前节点在父节点中的索引int idx = findKeyIndex(parent, current->keys[0]);if (idx > 0) {// 左兄弟存在BTreeNode<T>* leftSibling = parent->children[idx - 1];if (leftSibling->keyCount > minKeyCount) {// 从左兄弟借关键字borrowFromLeft(parent, idx);break;}}if (idx < parent->keyCount) {// 右兄弟存在BTreeNode<T>* rightSibling = parent->children[idx + 1];if (rightSibling->keyCount > minKeyCount) {// 从右兄弟借关键字borrowFromRight(parent, idx);break;}}// 无法借调，合并节点if (idx > 0) {mergeNodes(parent, idx - 1); // 与左兄弟合并} else {mergeNodes(parent, idx); // 与右兄弟合并}current = parent; // 继续检查父节点}return true;
}

辅助函数实现（部分）：

// 获取前驱关键字（左子树的最大关键字）
template <typename T>
T BTree<T>::getPredecessor(BTreeNode<T>* node, int index) {BTreeNode<T>* current = node->children[index];while (current->children[current->keyCount] != nullptr) {current = current->children[current->keyCount];}return current->keys[current->keyCount - 1];
}// 从左兄弟借关键字
template <typename T>
void BTree<T>::borrowFromLeft(BTreeNode<T>* parentNode, int rightChildIndex) {BTreeNode<T>* leftChild = parentNode->children[rightChildIndex - 1];BTreeNode<T>* rightChild = parentNode->children[rightChildIndex];// 右孩子关键字后移，腾出位置for (int i = rightChild->keyCount; i > 0; i--) {rightChild->keys[i] = rightChild->keys[i - 1];}// 父节点的关键字下移到右孩子rightChild->keys[0] = parentNode->keys[rightChildIndex - 1];rightChild->keyCount++;// 若不是叶子节点，左孩子的最后一个孩子移到右孩子if (leftChild->children[0] != nullptr) {for (int i = rightChild->keyCount; i > 0; i--) {rightChild->children[i] = rightChild->children[i - 1];}rightChild->children[0] = leftChild->children[leftChild->keyCount];rightChild->children[0]->parent = rightChild;leftChild->children[leftChild->keyCount] = nullptr;}// 左孩子的最后一个关键字上移到父节点parentNode->keys[rightChildIndex - 1] = leftChild->keys[leftChild->keyCount - 1];leftChild->keyCount--;
}// 合并节点（左孩子与右孩子合并）
template <typename T>
void BTree<T>::mergeNodes(BTreeNode<T>* parentNode, int leftChildIndex) {BTreeNode<T>* leftChild = parentNode->children[leftChildIndex];BTreeNode<T>* rightChild = parentNode->children[leftChildIndex + 1];// 父节点的关键字下移到左孩子leftChild->keys[leftChild->keyCount] = parentNode->keys[leftChildIndex];leftChild->keyCount++;// 复制右孩子的关键字到左孩子for (int i = 0; i < rightChild->keyCount; i++) {leftChild->keys[leftChild->keyCount + i] = rightChild->keys[i];}leftChild->keyCount += rightChild->keyCount;// 复制右孩子的孩子指针到左孩子（若不是叶子节点）if (leftChild->children[0] != nullptr) {for (int i = 0; i <= rightChild->keyCount; i++) {leftChild->children[leftChild->keyCount - rightChild->keyCount + i] = rightChild->children[i];if (leftChild->children[leftChild->keyCount - rightChild->keyCount + i] != nullptr) {leftChild->children[leftChild->keyCount - rightChild->keyCount + i]->parent = leftChild;}}}// 更新父节点的关键字和孩子指针for (int i = leftChildIndex; i < parentNode->keyCount - 1; i++) {parentNode->keys[i] = parentNode->keys[i + 1];parentNode->children[i + 1] = parentNode->children[i + 2];}parentNode->keyCount--;parentNode->children[parentNode->keyCount + 1] = nullptr;delete rightChild; // 释放右孩子
}

综合案例及应用

下面通过一个完整案例演示 B 树的插入、查找和删除操作：

// 打印B树（层序遍历）
template <typename T>
void BTree<T>::printTree() {if (root == nullptr) {cout << "B树为空" << endl;return;}vector<BTreeNode<T>*> queue;queue.push_back(root);while (!queue.empty()) {int levelSize = queue.size();for (int i = 0; i < levelSize; i++) {BTreeNode<T>* node = queue.front();queue.erase(queue.begin());// 打印当前节点的关键字cout << "[";for (int j = 0; j < node->keyCount; j++) {cout << node->keys[j];if (j != node->keyCount - 1) cout << ",";}cout << "] ";// 加入孩子节点（非叶子节点）if (node->children[0] != nullptr) {for (int j = 0; j <= node->keyCount; j++) {if (node->children[j] != nullptr) {queue.push_back(node->children[j]);}}}}cout << endl; // 每一层换行}
}// 析构函数辅助函数
template <typename T>
void BTree<T>::destroyTree(BTreeNode<T>* node) {if (node == nullptr) return;// 递归删除孩子节点for (int i = 0; i <= node->keyCount; i++) {destroyTree(node->children[i]);}delete node;
}// 测试案例
int main() {// 创建一个3阶B树（maxKeyCount=2，minKeyCount=1）BTree<int> bTree(3);// 插入关键字vector<int> keys = {10, 20, 5, 6, 12, 30, 7, 17};cout << "插入关键字: ";for (int key : keys) {cout << key << " ";bTree.insert(key);}cout << endl << "插入后B树结构（层序遍历）:" << endl;bTree.printTree();// 查找关键字int searchKey = 6;cout << endl << "查找关键字 " << searchKey << ": " << (bTree.search(searchKey) ? "找到" : "未找到") << endl;// 删除关键字int deleteKey = 10;cout << endl << "删除关键字 " << deleteKey << endl;bTree.remove(deleteKey);cout << "删除后B树结构:" << endl;bTree.printTree();return 0;
}