数据结构——哈希表、树、gdb调试、时间复杂度
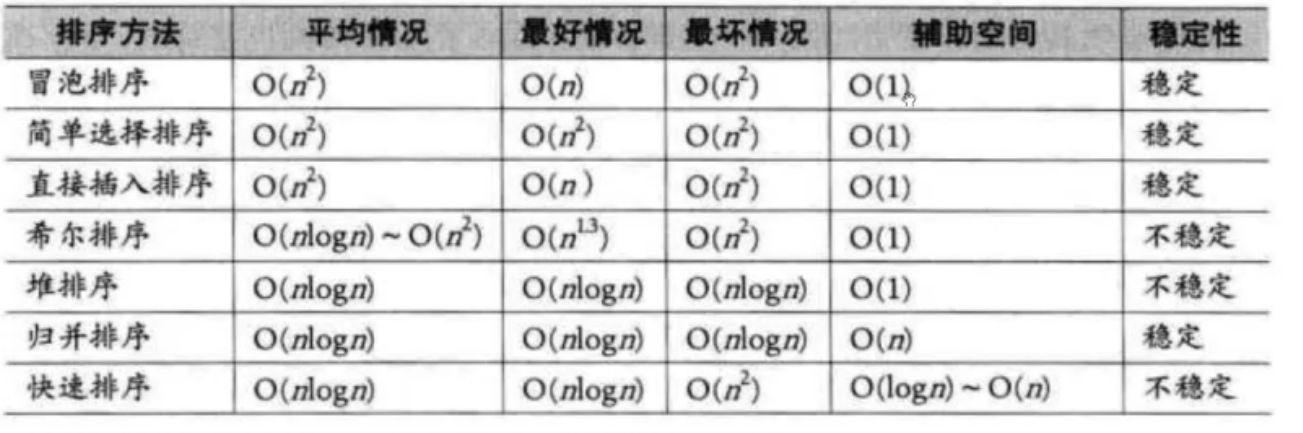
哈希表
将要存储的数据的关键字和位置之间,建立起对应的关系,这个关系被常委哈希函数。存储数据时,通过对应的哈希函数可以将数据映射到指定的数据位置,查找时,仍可通过该函数找到数据的存储位置,所以哈希表可以提高数据的查找率
哈希函数并不位移,由编写者指定,例如一次函数,求余等等等等
哈希冲突(哈希矛盾):不同数据通过函数映射到同一位置,为了解决该问题,通常有两种方法
(1)开放地址法:如果某一数据映射到的位置已经存有数据,就向下寻找,直到找到空位置并存入
(2)链地址法:就是将数组和链表结合到一起
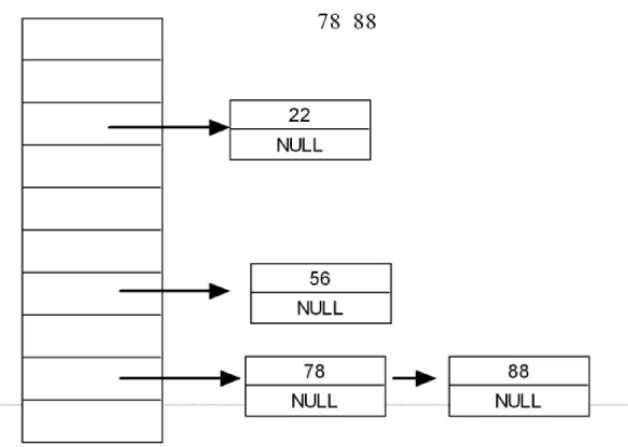
接下来便以链地址法的哈希表作为例子
定义
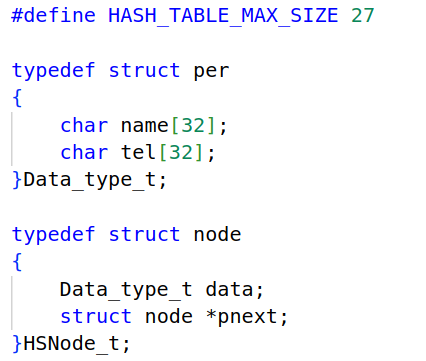

这里以名字与电话来作为结构体成员,结构体当作哈希表数组元素
创建

创建其实只需要类型名+变量名+元素个数形成数组(见定义最后一行),这里是用来比较名字的第一个字母,由于名字为字符串,所以这里采用了char型数组,通过ASCII码的“函数”形式确定元素在数组中的位置(数组大小为27,26个英文字母,1个其他字符)
头插
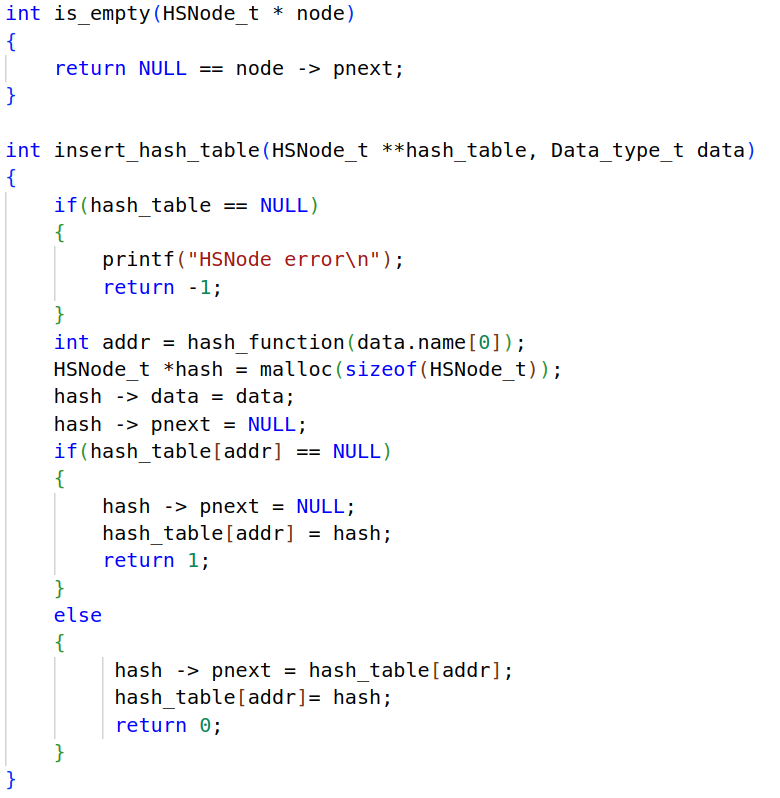
首先判断名字首字母是哪个元素,申请堆区空间,然后根据元素在字母表中的位置放在对应的哈希表中的位置,初始化结构体的成员,如果对应的数组元素空间为空,则直接插入,如果不是,则按照单向链表的操作头插入以该数组元素位置为链表对象的链表中
值得说明的是形参的二级指针,因为哈希表为结构体数组,如果是一级指针,则无法做到修改数组内的元素(一维数组可以理解为一个*),所以在此处用了二级指针
遍历
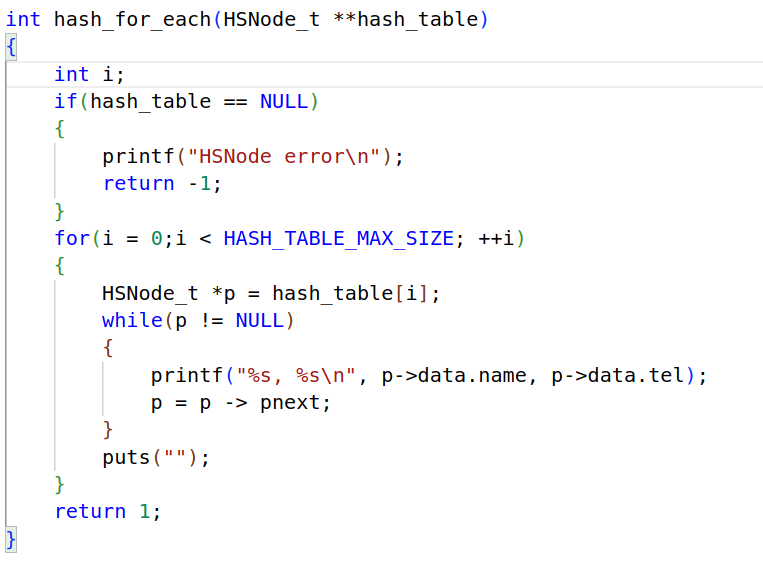
由于哈希表可以说是个数组,所以可以采用数组的遍历形式
查找
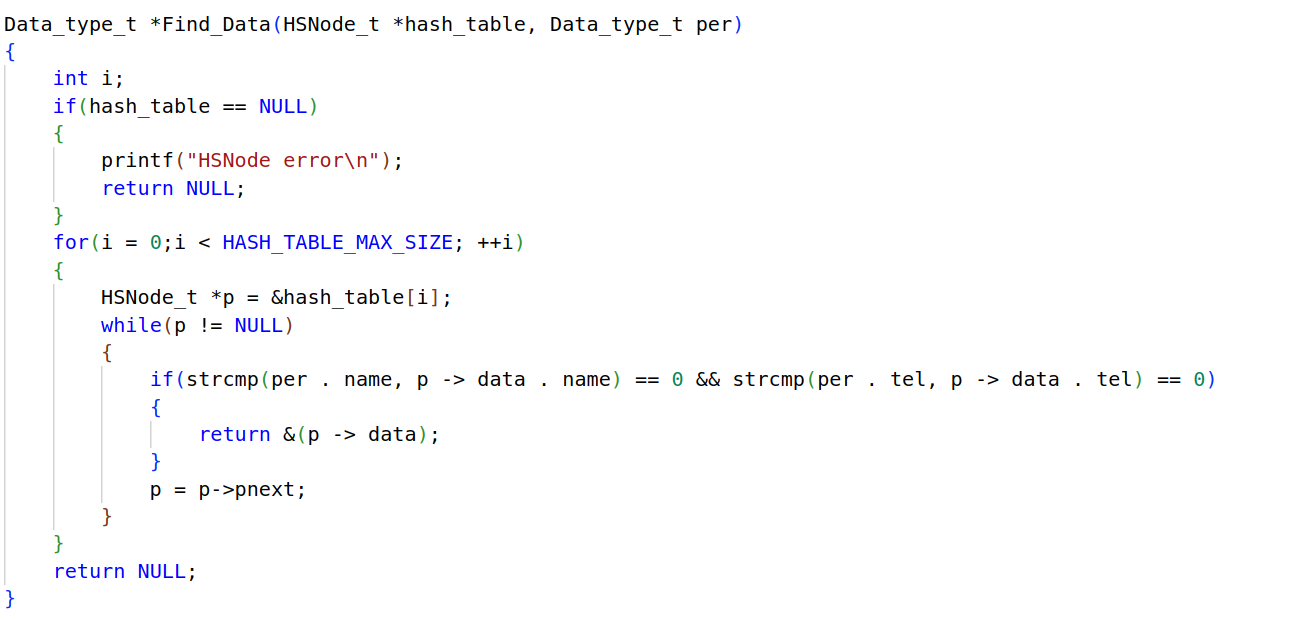
根据结构体去寻找,具体的结构体可以通过回调函数的返回值,由于是要查找,所以结构体中的两个成员都要一一匹配,同时由于都是字符串,所以需要调用string函数
销毁

同样是二级指针,为了改变指向该哈希表的指针,所以采用了指针的指针,先销毁哈希表每个元素含有的链表,再销毁哈希表数组部分
树
树:n(n>=0)个结点的有限集合,当n==0时,为空树
性质:在任意一个非空树中
(1)有且仅有一个特定的根节点
(2)n>1时,其余结点分为m个互不相交的有限集合,每个集合又是一个树,称为子树
(3)树为一对多的结构,不是多对多,所以不存在横向指向
度:结点拥有子树的个数称为结点的度。度为0的结点为叶子结点,不为0则为分支结点
树的度数:从这棵树中,最大的结点的度数,为树的度数
树的深度或高度:从根开始,根为第一层,根的孩子结点为第二层,以此类推
树的存储:顺序结构和链式结构
二叉树
树中有一种特殊类型,称为二叉树,它是n个结点的有限集合,集合要么为空树,要么由一个根节点和两棵互不相交,分别称为根节点的左子树和右子树的二叉树组成
特点:1,每个结点最多两个子树
2,左子树和右子树都是有顺序的,次序不可颠倒
3,如果某个结点只有一个子树,也要区分左子树和右子树
特殊类型的二叉树
(1)左斜树、右斜树:所有结点只有左子树、所有结点只有右子树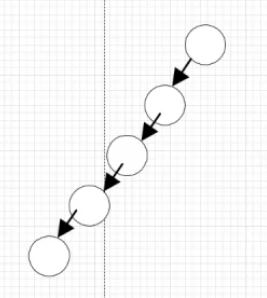
(2)满二叉树:所有结点均存在左右子树,并且叶子都在同一层上
(3)完全二叉树,对于一棵由n个结点的二叉树按层序编号,如果编号为i的结点对于同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同
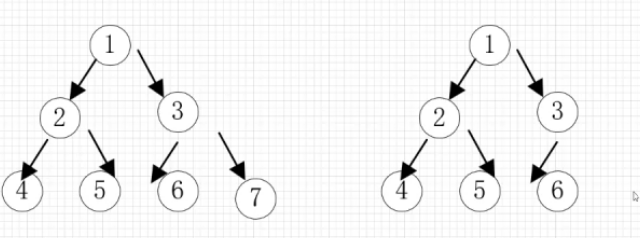
左侧为满二叉树,右侧为完全二叉树,对于右侧,如果5号结点删除,则6号结点改为5号结点,那么就不是完全二叉树。满二叉树一定是完全二叉树
特性:1,在二叉树的第i层最多有2^(i - 1)个结点
2,深度为k的二叉树最多有2^k - 1个结点
3,任意一个二叉树T,如果其叶子节点的个数为n1,度数为2的结点数位n2,则n1 = n2 + 1
4,有n个结点的完全二叉树,其深度为(lgn/lg2)+ 1
树的遍历
前序遍历:根左右,即先访问根结点,再左结点,在右结点
中序遍历:左根右,即先访问左结点,再根结点,在右结点
后序遍历:左右根,即先访问左结点,再右结点,在根结点
例:
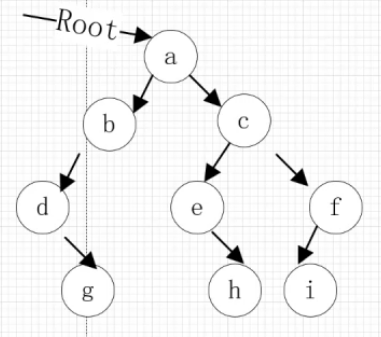
遍历分别为:abdgcehfi dgbaehcif gdbheifca
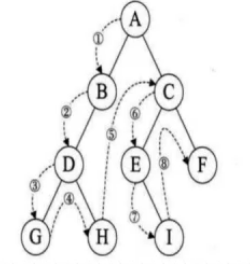
遍历分别为:ABDGHCEIF GDHBAEICF GHDBIEFCA
二叉树的操作
定义

静态创建
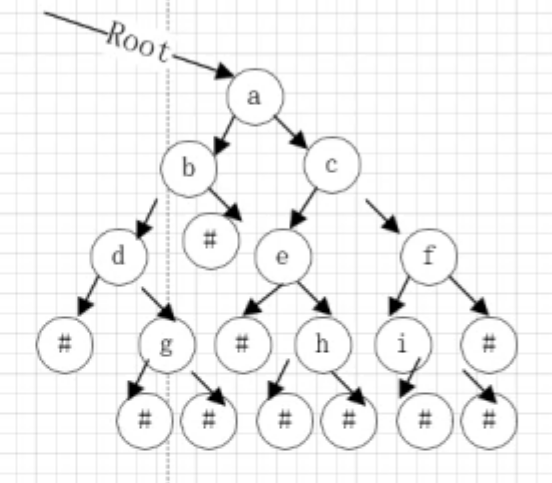

静态创建,就是在创建之前树已经规定好了,并不像之前链表一类,来一个结点插一个结点
先一个个取出data[]中的元素,所以ind++,如果c=‘#’,则表示该结点没有后继结点,并令根节点为空结点,函数终止,如果不是,则申请结点空间,在申请的结构体空间中装入数据,并以其左右结点为新的根节点再次引用该函数,直到叶子节点,并将叶子节点制空。整体为函数的递归,因为树的每一个子树都是二叉树,结构相同
前序遍历

先遍历根结点,再左再右
中序遍历

后序遍历

gdb

gdb可用来调试代码运行,用于观察代码的具体运行状况 ,接下来以树的代码为例,按照上图来演示2的步骤和部分密令
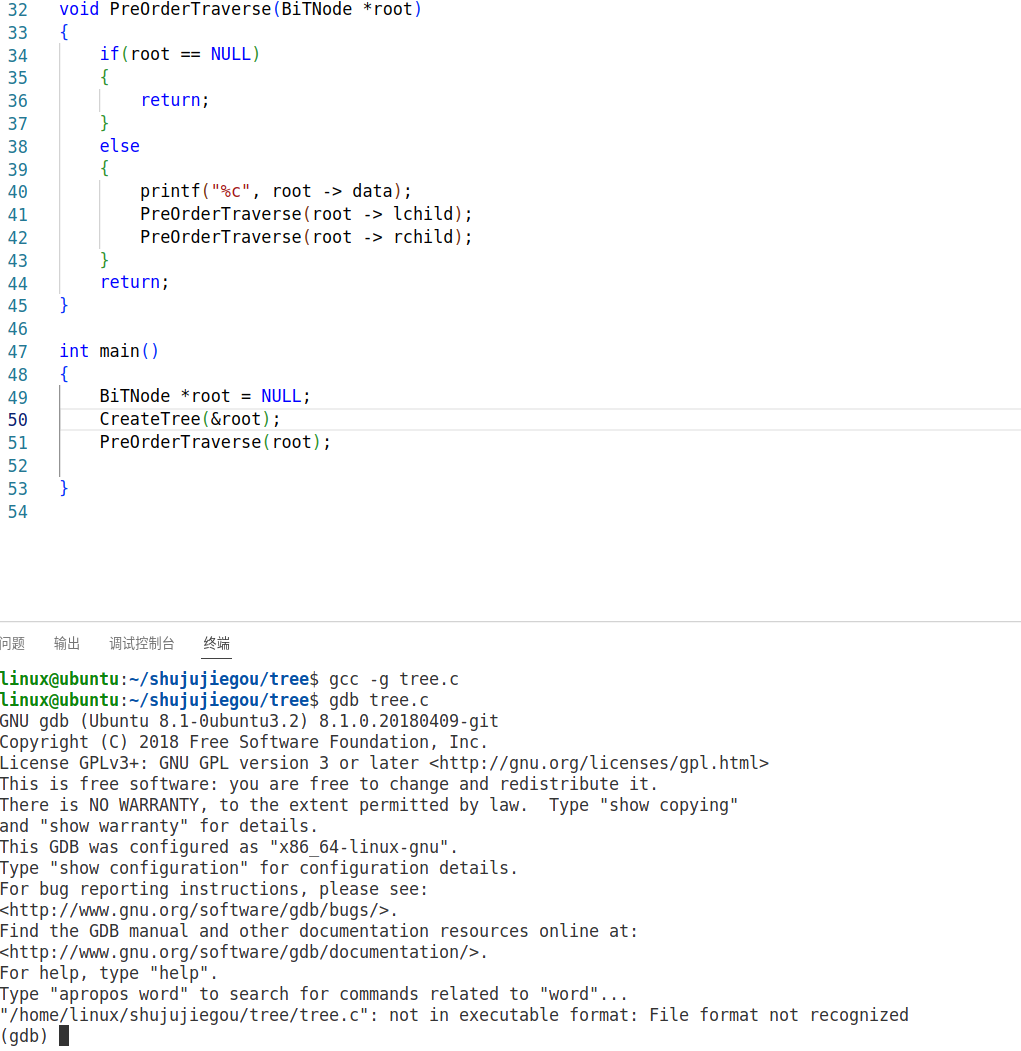
这是1)与2)
![]()
这是3),意思是在51行设置了一个断点,然后等待下一步指令
![]()
这也是3),在该函数处设立断点,函数可以用Tab补齐

这是4),因为上面在51处设立了一个断点,所以程序到51行停止,而第二个51后的代码表示的是将要运行的代码,还没运行
![]()
这是5),表示下一步应该执行哪一行,这一行代码内容是什么

这是6),p加空格加变量,可以显示出变量的具体情况
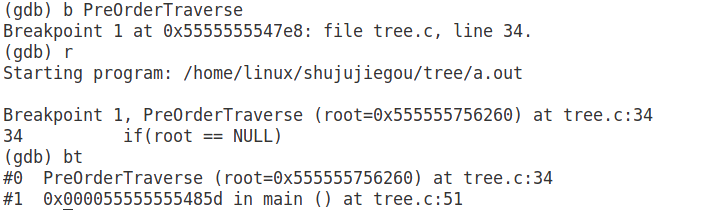
这是bt密令,会显示当前栈结构
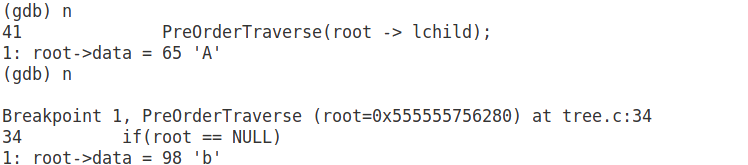
这是display密令
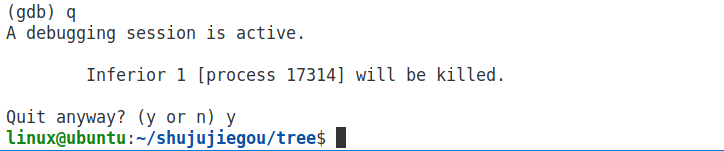
退出gdb
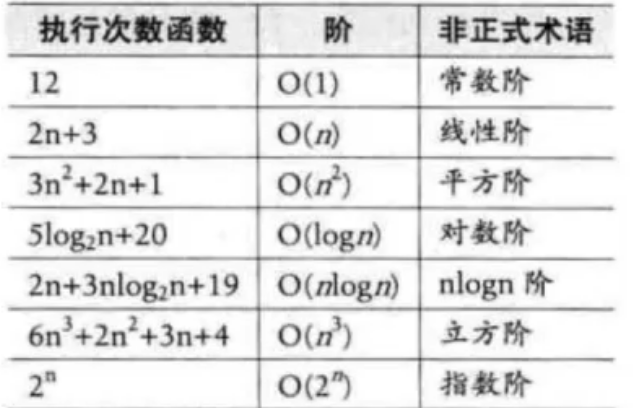
时间复杂度