【深度学习2】logistic回归以及梯度下降
逻辑回归(Logistic Regression)是一种广泛应用于分类问题的统计学习方法,尤其适用于二分类任务(如 “是 / 否”“正 / 负”)。本质上是一种分类算法,通过建立输入特征与输出类别之间的概率关系来进行预测。
二分分类
二分分类输出是1 / 否0
目的是训练出一个分类器,特征向量x作为输入(如图片的像素点),输出预测结果标签y是1/0
常用符号:
- (x,y)表示一个单独的样本
- x是n维特征向量
- y∈{1, 2}
- m表示训练集样本个数
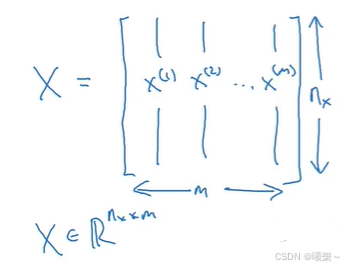
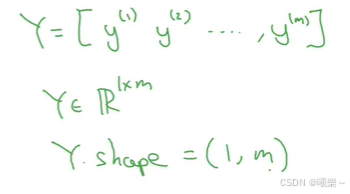
逻辑回归
z越大y越靠近1,反之y靠近0.
损失函数(Loss function)
损失函数用于衡量单个训练样本的效果
损失函数用来衡量预测输出值和实际值y有多接近。
损失函数越小(误差越小)越好。
逻辑回归中常用的损失函数是交叉熵损失函数(Cross-Entropy Loss):
成本函数J(cost function)用于衡量参数w和b的效果
J(w, b)= 所有损失函数的平均值
梯度下降法(gradient descent)
成本函数J是一个关于参数w和b的凸函数,要找到它的最小值点(平均损失最小)
梯度下降(就是要求导):从初始点开始(逻辑回归可以任意选一个初始点,因为成本函数是凸函数),朝最陡的下坡方向走一步(尽快的下降),通过几次梯度下降的迭代找到那个最小值点(全局最优解)
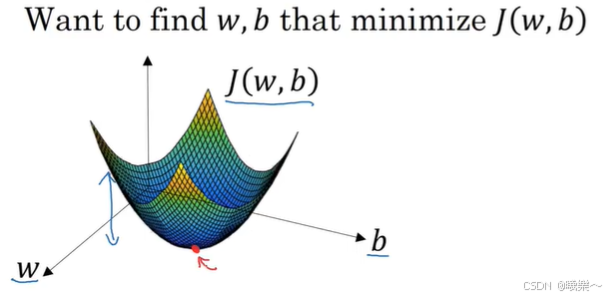
w、b的迭代:
其中α是学习率(learning rate),后面乘上斜率(导数)实现值减小
前向传播和反向传播
- 前向传播计算神经网络的输出
- 反向传播计算对应的梯度(导数)
下图蓝色部分是前向传播,红色部分是反向传播(用于计算J对其他变量的倒数):
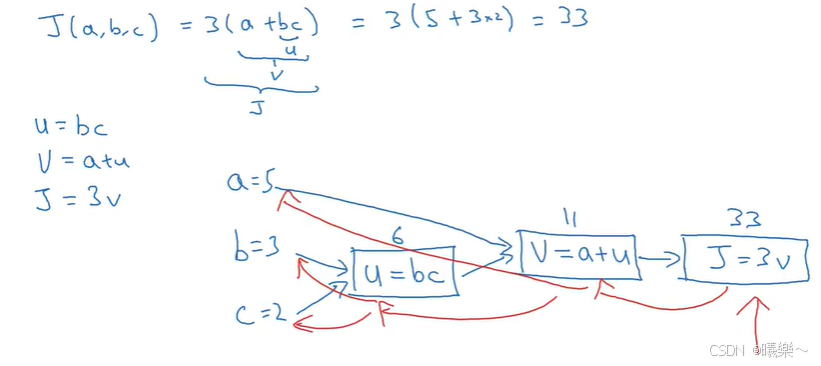
在编写代码时上述例子J对其他变量的求导写作dJvar/dvar
逻辑回归中的梯度下降
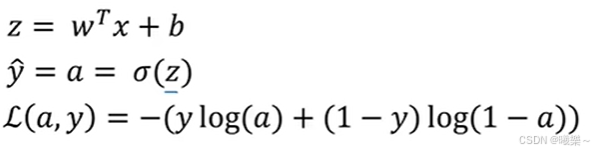
假设这个函数中有两个特征x1和x2,会得到下面一个传播过程
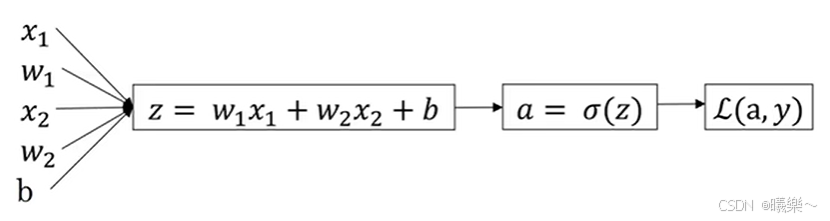
反向传播计算dL/da-->dL/dz-->dL/dw和dL/db,最后对w和b的值进行迭代。
多个样本的梯度下降
上面讲的都是二分类,只有两个特征样本。
m个样本的成本函数公式为:
梯度下降:
- 参数初始化全为0,
- 前向传播计算出J,
- 循环计算每个特征对于J的倒数,
- 得到各自的w和b

