【误差理论与可靠性】第二章 可靠性的基本概念和参数体系
附上我2025年2月22日画的002.joker。
用手绘板开始画画,先从临摹开始。

目录
2.1可靠性的定义
2.2 可靠性特征量
2.3 维修性及其特征量
2.4 有效性的特征量
2.5 可靠性中常用的概论分布
1.二项分布
2.指数分布
3.泊松分布
4.正态分布
5. 对数正态分布 ( 为一随机变量)
2.6 失效数据的基本处理方法
关注作者了解更多
我的其他CSDN专栏
毕业设计
求职面试
大学英语
过程控制系统
工程测试技术
虚拟仪器技术
可编程控制器
工业现场总线
数字图像处理
智能控制
传感器技术
嵌入式系统
复变函数与积分变换
单片机原理
线性代数
大学物理
热工与工程流体力学
数字信号处理
光电融合集成电路技术
电路原理
模拟电子技术
高等数学
概率论与数理统计
数据结构
C语言
模式识别原理
自动控制原理
数字电子技术
关注作者了解更多
资料来源于网络,如有侵权请联系编者
内容提要
2.1 可靠性的定义
2.2 可靠性特征量
2.3 维修性及其特征量
2.4 有效性的特征量
2.5 可靠性中常用的概率分布
2.6 处理失效数据的基本方法
2.7 处理失效数据的一个案例
2.1可靠性的定义
可靠性(reliability):产品在规定的条件下和规定的时间内完成规定功能的能力。
产品:可以是系统、子系统、部件等
规定的条件:使用条件,运输、储存、使用时的环境条件(温度、压力、湿度、载荷、振动、腐蚀、磨损等等),使用方法、维修水平等
规定的时间:R是t的函数,t可以是时间、起落次数、里程等
规定的功能:故障、不能工作、参数漂移,要有故障判据
可靠性分为:
固有R:在生产过程中已经确立了的可靠性
使用R:使用环境、操作水平、保养与维修等因素
基本R:产品在规定条件下,无故障的持续时间或概率。反映维修人力和后勤保障等要求
任务R:产品在规定的任务剖面内完成规定功能的能力
2.2 可靠性特征量
1.可靠度(reliability)与不可靠度
可靠度: R=R(t)=P(E)=P(T ≥ t),
(t ≥ 0)
E:“产品在规定条件下和规定时间内完成规定功能”这一事件
T:“产品正常工作时间”这一随机变量
t :指定某一规定时间
不可靠度 :

(不可靠度函数或失效概率函数)
由此式可知:F(t)是随机变量 T 的分布函数,它的密度函数为:

(此处也叫失效密度函数或故障密度函数)
由上式:


用观测值表示 R(t), F(t)(无参数方法)
设有N个同型号产品,从开始工作 0 到任意时间 t 时,有n(t)个失效,则有N- n(t)个能正常工作



变化规律:
是否考虑过 R(t), F(t), f(t) 的量纲?(假设t的单位为 月)
能否解释一下这张图表示的含义?
f(t)是否可能大于1,产品故障时间为1.5的概率为多少?
对于某一个产品如果过了f(t) 的波峰还在运行,那么是否说明该产品失效的风险变低了?

2.失效率/故障率 (hazard rate/failure rate)(t)
工作到某时刻 t 时尚未失效或故障的产品,在 t 时刻以后的下一个单位时间内发生失效或故障的概率。
设有N个产品从t=0时开始工作。

按定义:观测值t内(平均失效率):

瞬时失效率(或简称失效率):

在某零件的一次可靠性试验中,到50h时,还有100个仍在工作。工作到51h时,失效了1个。在第52h内失效了3个。试求这批零件工作50h和51h时的平均失效率 。
由上式:








失效率是一种概率吗?
失效率是一种概率密度函数吗?
失效率是一种条件概率密度函数吗?
失效率有量纲吗?
典型失效率曲线:

3.平均寿命

上述MTTF与MTBF本质上是一样的,因此统称为 平均寿命,用 θ 表示

如已知产品总体的失效密度函数 f(t),则




4.可靠寿命、中位寿命、特征寿命



2.3 维修性及其特征量
维修性:在规定条件下使用的产品,在规定的时间内,按规定的程序和方法进行维修时,保持或恢复到能完成规定功能的能力。
维修度(maintainability):对可修产品在发生故障或失效后,在规定的条件下和规定的时间(0,τ)内完成修复的概率。 如T表示维修时间(实际修复):T为一随机变量

M(τ)表示从0开始到某一时刻τ以内完成维修的概率
是对τ的累积概率
是对τ的非降函数



![]()

![]()


2.4 有效性的特征量
有效性是可靠性与维修性的一个综合特征
用有效度(availability)度量有效性:可维修产品在某时刻 t 具有或维持其功能的概率。用 A(t) 表示 有效度又称为利用率、可用度等(对不可修产品,有效度等于可靠度)
瞬时有效度A(t) :在某一特定瞬时,可能维修的产品保持正常使用状态或功能的概率。只反映 t 时刻产品的有效度,而与 t 时刻以前是否失效无关

2.5 可靠性中常用的概论分布
1.二项分布
二项分布满足以下基本假定: 试验次数n是一定的
每次试验的结果只有两种,成功或失败;
成功的概率为p,失败的概率为q,p+q=1
p,q为常数
所有试验是独立的
在n次试验中,r次成功和n-r次失败的概率 为

若一个系统含有 n 个相同的元件,至少有 r 个元件完好称系统完好,那么系统完好的概率为

(式中p表示一个元件完好的概率
例:一架飞机有三个着陆轮胎,如果不多于一台轮胎爆破,飞机便能安全着陆。试验表明,轮胎平均每着陆1000次发生一次爆破,求飞机安全着陆的概率。



2.指数分布
如果产品的故障发生时间符合指数分布,那故障率函数 λ(t) 为多少?

指数分布的无记忆性:
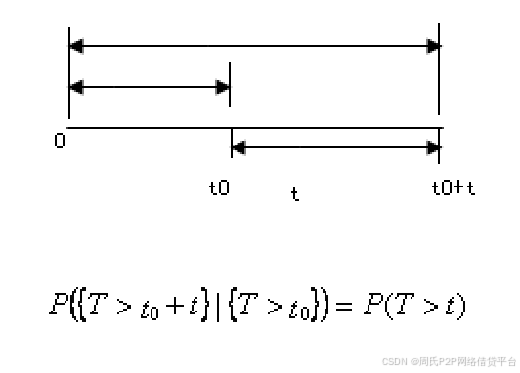

上式表明: 若元件服从指数分布,那么元件在 t0 以前可靠工作的条件下,在 t0 +t 期间仍然正常工作的概率等于元件在 ( 0, t ) 正常工作的概率,与过去的工作时间 t0 无关,这种特点称为无记忆性,只有指数分布具有这种特点。
例:某装置的寿命服从指数分布,均值为500h,求该装置至少可靠运行600h的概率,若有三台同样的装置,在头400h里至少一台装置故障的概率。




3.泊松分布
假设单位时间内某事件发生的平均发生率为 ,求在时段(0, t)中发生x次的概率 。

对于泊松分布:

泊松分布的假设: 事件发生率λ为常数,不随时间变化 在任何相同长度的时间间隔发生某一数量的事件的概率是相同的 事件的发生是相互独立的 思考题:当泊松分布的假设条件符合时,各相邻随机事件的时间间隔服从什么分布?
例:某大型网络处理系统的平均故障率是每三个月一次,求一年发生5次以上故障的概率。

![]()


4.正态分布

5. 对数正态分布 ( 为一随机变量)

当失效时间符合对数正态分布时的可靠性指标:




2.6 失效数据的基本处理方法
参数法:并不事先假设失效数据所符合的分布。

其他的无参数法:如混合高斯模型。 无参数法的优点:灵活,在各种情况下都可以用。 无参数法的缺点:需要大量长时间的实验数据。很难用简练的数学公式表示。
参数法:假设失效数据符合某一个已经知道的分布。 参数法使用时要解决的问题: 参数估计问题 点估计、最大似然估计、做图法估计 模型检验问题 画图法、假设检验 模型选择问题 BIC、AIC、AICc
参数估计问题:
例:有一组加速生命实验的产品失效时间数据(单位 小时):181.9034, 23.0314, 116.7271, 63.7650, 179.7886 50.7528, 133.5710, 42.4527, 37.2203, 29.0150, 79.7305, 247.9067, 147.4134, 9.0650, 188.1391, 19.1382, 61.9260, 0.3873, 254.8799, 81.4912 假设我们已知其符合指数分布:
点估计法:

评价点估计的指标:无偏性、有效性、一致性
最大似然估计: 分两步进行(1)推导似然函数(2)求似然函数的最大值

最大似然函数法的优点:一致性、有效性比较好。可以求出置信区间。上例中可以得到95%置信区间为(0.0152, 0.0063)
图形法:可以同时用于检验分布拟合情况和参数

