MPC-in-the-Head 转换入门指南

1. 引言

本文将探讨构建零知识证明（ZKP）的一种非常有趣的方法：

• MPC-in-the-Head Transformation（转换）。
  • 该方法最早由 2007 年的论文 Zero-knowledge from secure multiparty computation 提出，通常被称为 IKOS 转换，该名称来源于论文作者的首字母缩写。
  • 该转换允许从任意的 MPC 协议（将其视为黑盒）构建零知识证明系统。

本文将介绍 MPC 协议背后的直觉、最初的转换技术，并探讨该构造如何应用于开发后量子签名方案。

2. 何为MPC？

安全多方计算（MPC） 是一种密码学技术：

• 允许多个参与方共同计算一个函数的结果，同时各自保留输入的私密性。
• 每个参与方都持有自己的私有输入，目标是对所有私有输入执行某个预定的函数。
• 协议结束时，每个参与方只应学习到该函数的输出，而不能得知其他参与方的输入信息。
  

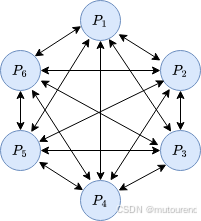
3. 一个简单的MPC协议

MPC 协议中常用的示例是如下场景：

• 假设一家公司的一群员工想要知道全体员工的平均工资，但又不想暴露自己的工资。
  • 在这个设定中，每个员工持有一个私有输入 $S_i$，表示自己的工资。

假设所有计算都在某个素域 ${\mathbb{F}}_p$ 上进行，希望构建一个协议，用于计算所有员工私有输入（工资）的总和 $\sum S_i\in {\mathbb{F}}_p$。随后，平均工资可以在明文中通过总和除以员工数量来计算。

该协议分为三个步骤：

• 1）输入共享（input sharing）
• 2）本地累加（local accumulation）
• 3）重构（reconstruction）。

3.1 输入共享

设想1号员工持有自己的工资 $S_1$。其首先会对 $S_1$ 进行加法秘密共享（additive secret sharing），也就是说将该值“分割”为 $n$ 个份额：
$$[S_1{]}_1,[S_1{]}_2,\dots ,[S_1{]}_n$$

这些份额都是域中的元素，满足它们的总和等于原始值 $S_1$：
$$S_1=[S_1{]}_1+[S_1{]}_2+\dots +[S_1{]}_n$$

在实践中，计算方式如下：首先从 ${\mathbb{F}}_p$ 中均匀随机采样前 $n-1$ 个份额，然后计算最后一个份额为：
$$[S_1{]}_n=S_1-\sum _{i=1}^{n-1}[S_1{]}_i$$

显然，如果前 $n-1$ 个份额是从 ${\mathbb{F}}_p$ 中均匀随机选择的，那么最后一个份额也在 ${\mathbb{F}}_p$ 中是均匀分布的（即使只有其中一个是均匀随机的也同样成立）。这是一种实现完美隐私（perfect privacy）的简单方式：

• 即使攻击者看到最多 $n-1$ 个份额，也无法得知原始值 $S_1$ 的任何信息。

3.2 本地累加（Local accumulation）

在这一步中，每位员工将自己生成的第 $i$ 个份额发送给第 $i$ 个参与方。以1号员工为例，他们会将 $[S_1{]}_2$ 发送给2号员工，$[S_1{]}_3$ 发送给3号员工，依此类推。1号员工最终会从其他员工那里接收到以下份额：
$$[S_2{]}_1,[S_3{]}_1\dots ,[S_n{]}_1$$

同时他们还持有自己生成的份额 $[S_1{]}_1$。

接下来，每位员工可以将所有收到的份额进行本地累加（Local accumulation）：
$$[S{]}_1=[S_1{]}_1+[S_2{]}_1+\dots +[S_n{]}_1$$

然后将这个累加结果 $[S{]}_1$ 发送给其他所有员工。

3.3 重构（Reconstruction）

最终，每位员工都将收到其他员工累加的份额：
$$[S{]}_1,[S{]}_2,\dots ,[S{]}_n$$

因此，每个人都可以独立地重构最终输出，即将所有 份额 相加：
$$S=[S{]}_1+[S{]}_2+\dots +[S{]}_n$$

这个结果正是所有私有输入的总和。

要理解为什么这样有效，可以注意到，在这种秘密共享方案中，份额具有加法同态性（additive homomorphism）：

• 两个 秘密的份额 相加，得到的是这两个 秘密和 的份额。

在这个具体案例中，之所以能使用这么简单的协议，是因为要共同计算的函数对私有输入来说是线性的。而一般情况下，MPC 协议可以用于计算任意函数，但这就需要更复杂的技术。

若想深入了解 MPC 构造的原理，一个很好的起点是：

• Y. Lindell 2020年的综述论文Secure Multiparty Computation (MPC)。

4. MPC 协议的性质

一个 MPC 协议应满足两个主要性质：

• 正确性（Correctness）：协议的输出应该是函数的正确输出，就像各方在明文下直接计算的结果一样。
• 隐私性（Privacy）：各方除了函数的输出外，不应获知其他参与方的任何私有输入信息。

一般来说，假设有一些参与方可能会被腐化，也就是说，攻击者可能能够看到这些参与方的输入以及它们之间交换的消息。如果一个 MPC 协议即使在最多 $t$ 个参与方被腐化的情况下仍然能保持隐私性，则称该协议是 $t$-隐私（$t$-Private） 的。如果被腐化的参与方超过 $t$ 个，那么可能就会泄露关于诚实参与方私有输入的信息。

在 本文所提及的“MPC-in-the-Head 转换” 这个基本的转换中，只要求 2-隐私（2-Privacy） —— 也就是说，只要腐化的参与方不超过两个，隐私性就仍然能够被保证。

此外，本文所描述的 MPC 协议（“MPC-in-the-Head 转换” ）只需要在半诚实模型（semi-honest model）下是安全的。也就是说，假设所有参与方都会诚实地执行协议，但可能试图在执行过程中尽可能多地获取信息。这类参与方通常被称为“诚实但好奇（honest but curious）”。如，前文描述的那个简单协议就假设所有参与方都诚实地遵守协议流程：如果有参与方偏离协议执行流程，最终输出可能会被错误地计算出来。

最初的 IKOS 转换 将底层的 MPC 协议视为一个黑盒，但需要指出的是，在一些效率更高的方案中，MPC 协议是经过特别设计的，以便在应用转换时能导出一个高效的零知识证明系统。

5. MPC-in-the-Head 转换

“MPC-in-the-Head 转换的目标是：

• 利用具备上述性质的任意一个 MPC 协议，来构建一个零知识证明系统，用于某个NP关系 $\mathcal{R}\subseteq \mathcal{X}\times \mathcal{W}$。

在这种新的设定中，有两方参与者：

• 证明者（prover）
• 和 验证者（verifier）。

证明者希望让验证者相信自己知道一个见证 $w$，满足 $(x,w)\in \mathcal{R}$，其中 $x$ 是公开输入。

举个例子，关系 $\mathcal{R}$ 可以是 SHA-256 哈希函数的原像关系：
$$\mathcal{R}=\{(x,w)\mid \text{SHA256}(w)=x\}$$

证明者将见证 $w$ 拆分为加法份额 $w_1,w_2,\dots ,w_n$，使得所有份额的和等于原始的见证 $w$：
$$w=w_1+w_2+\cdots +w_n$$

接着，证明者会在“自己的脑海中（in its head）”模拟整个 MPC 协议：

• 可以想象这是在导演一场由 $n$ 个布偶角色参与的小型舞台剧，每个角色代表一个协议参与方。
• 这些“布偶”按照一套脚本（即 MPC 协议的执行步骤）进行互动。
• 第 $i$ 个参与方持有份额 $w_i$ 作为自己的私有输入，所有参与方都共享公开输入 $x$。
• 这些模拟的参与方共同计算的函数如下：如果关系满足就返回 1，否则返回 0：
  $$f(x,w_1,w_2,\dots ,w_n)=\{\begin{array}{ll}1& \text{if }\mathcal{R}(x,w_1+w_2+\dots +w_n)\\ 0& \text{otherwise}\end{array}$$

请注意，由于关系 $\mathcal{R}$ 属于 $\mathsf{NP}$，它拥有一个多项式时间的验证算法。因此函数 $f$ 也是高效可计算的：

• 它只需要对局部见证进行求和，然后验证该关系是否成立。

举一个具体的例子：对于 SHA-256 原像关系，MPC 协议要计算的函数如下所示：

def f(x, w_1, w_2, ..., w_n):w = w_1 + w_2 + ... + w_nif SHA256(w) == x:return 1else:return 0

在实际中，这个函数通常被表示为定义在某个有限域上的算术电路（arithmetic circuit） $C$。

在模拟完 MPC 协议后，证明者会为每个参与方生成一个 view（视图）。每个视图包含：

• 该参与方的私有输入；
• 该方在模拟执行期间发送和接收的所有消息。

如，如果第 $i$ 个参与方向第 $j$ 个参与方发送了一条消息 $m$，那么：

• 第 $i$ 方的视图中将包含一个外发消息 $\text{out}(j,m)$；
• 第 $j$ 方的视图中将包含一个接收消息 $\text{in}(i,m)$。

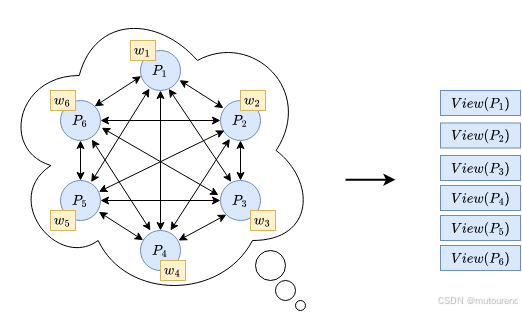
接下来，证明者会将所有参与方视图的承诺（commitment）发送给验证者。承诺方案（commitment scheme）是一种密码学原语：

• 它允许一方对某个值进行承诺（即固定但不公开），并在之后可以选择打开该承诺来揭示该值。

一个承诺 $c=Comm(x)$ 应该满足以下两个性质：

• 隐藏性（hiding）：该承诺 $c$ 不泄露任何关于值 $v$ 的信息；
• 绑定性（binding）：证明者无法在之后打开一个不同的值 $y\ne x$，却让验证者相信它是 $c$ 的合法打开值。

一个具体示例是，使用抗碰撞哈希函数（collision-resistant hash function）来实现简单的承诺方案：

c = H(v || r)

其中 $v$ 是要承诺的值，$r$ 是某个随机数。

def commit(x: bytes) -> bytes:nonce = random(16)return sha256(x + nonce)def verify_opening(x: bytes, nonce: bytes, commitment: bytes) -> bool:return len(nonce) == 16 and sha256(x + nonce) == commitment

在证明者将每个视图的承诺发送给验证者之后，验证者会随机选择两个参与方（设为第 $i$ 个和第 $j$ 个），并要求打开这两个参与方的视图。随后，证明者将这两个视图以明文形式发送给验证者。

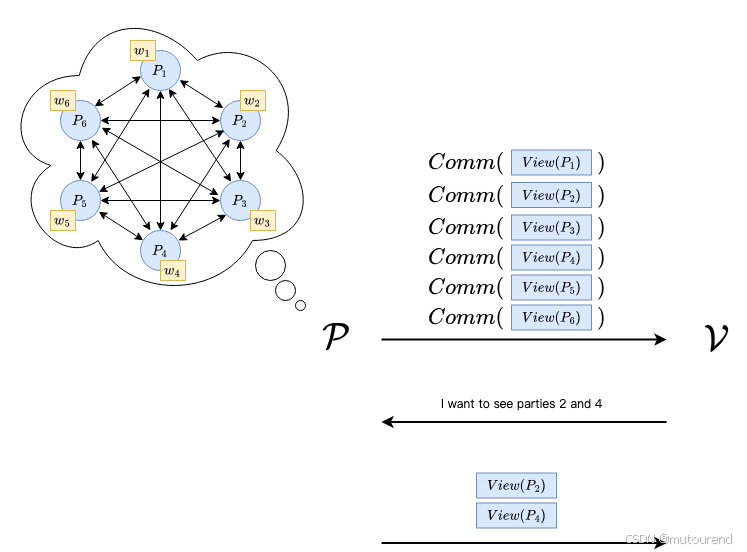
此时，验证者可以获得以下信息：

• 两个输入 $w_i$ 和 $w_j$；
• 两个参与方（$i$ 和 $j$）在协议执行过程中发送和接收的所有消息记录。

验证者会检查以下几点：

• 所给视图是对应承诺的有效打开值；
• 第 $i$ 个和第 $j$ 个参与方诚实地遵守了协议流程；
• 两个视图彼此一致，即任何一条双方之间交换的消息，在两边的记录中内容完全一致；
• 两个打开的视图一致地认为函数的输出是 $1$（即计算结果正确）。

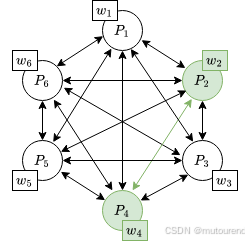
Soundness（完备性）：

• 该方案的完备性（soundness）直接依赖于底层 MPC 协议的正确性。假设 MPC 协议具有完美正确性，那么如果证明者诚实地模拟协议执行，输出结果必然是正确的。
  但如果证明者尝试作弊，它必须至少在一个参与方的视图中作弊。这意味着总会有至少一对视图与诚实执行的协议不一致。验证者随机选择两方来检查的情况下，选中这一对不一致视图的概率是 $1/\left(\genfrac{}{}{0ex}{}{n}{2}\right)$，因此，证明者成功作弊的概率是：
  $$\epsilon =1-1/\left(\genfrac{}{}{0ex}{}{n}{2}\right)$$
  如同所有零知识证明系统一样，只要重复执行足够多次，就可以将 soundness error（证明者成功作弊的概率）降低到指数级小。

Zero-knowledge（零知识性）：

• 零知识性（Zero-knowledge）则直接基于底层 MPC 协议的隐私性。只需注意到，验证者最多只能看到两个参与方的视图，而由于假设底层的 MPC 协议是 $2$-Private 的，因此验证者无法从中获得关于其他参与方私有输入的任何信息。此外，知道 $w_i$ 和 $w_j$ 也不会泄露任何关于完整见证 $w$ 的信息。

5.1 消除交互（Removing interaction）

该协议具有一个非常优美的特性：

• 它是一个公共随机币协议（public-coin protocol）。

这意味着验证者不参与任何复杂操作，只需采样随机挑战并发送给证明者即可。正因为如此，可以使用标准的 Fiat-Shamir 转换 将该协议转化为非交互式零知识证明（NIZK）。

5.2 协议改进（Improvements）

虽然上述协议在实践中效率较低，但后续的一些具体实现对该基本构造进行了大量优化。其中一个导致效率低的主要原因是：

• 为了使 soundness error（欺骗成功的概率）足够低，证明者必须执行许多轮协议。
  • 这是因为在每一轮中，验证者只打开两个视图，因此单轮的 soundness error 较高。

举一个具体例子，如果 $n=8$，那么证明者在单轮中成功作弊的概率为：
$$1-1/\left(\genfrac{}{}{0ex}{}{8}{2}\right)\approx 96.4\text{\%}$$

一个直接的改进方法是使用一个 $(n-1)$-Private 的 MPC 协议，使得证明者可以安全地打开除一个之外的所有视图，而不会泄露隐私（不牺牲零知识性）。在这种设定下，验证者只选择一个视图保持私密，而证明者向验证者公开其余所有参与方的视图。

这种方法显著降低了 soundness error，此时：

• 骗局必须发生在那个被保留不公开的参与方身上，而被选中作为隐藏方的概率为 $\frac{1}{n}$；
• 因此，单轮的 soundness error 变为：
  $$\epsilon =\frac{1}{n}$$

和之前一样，当 $n=8$ 时，成功欺骗的概率为：
$$\frac{1}{8}\approx 12.5\text{\%}$$

6. 应用于后量子签名的构造

由 MPC-in-the-Head 转换所构造的零知识证明系统具有一些非常有趣的特性：

• 如果使用的是一个抗量子攻击的 MPC 协议，那么转换后的零知识证明方案也将具备后量子安全性，因为整个转换仅依赖于基础的密码学承诺（commitment），这些承诺可以通过抗碰撞哈希函数来实现，如 SHA3。
• 证明的大小与电路规模线性相关，且具有非常小的常数系数，因此对于门数量较少的电路，在实践中是高效的。
• 证明者和验证者的时间复杂度均与电路规模线性相关，基本上两者所需的计算量是相当的。

这使得该方案在构建后量子数字签名方案方面非常有吸引力。一般而言，要从零知识证明系统构造一个签名方案，首先选择一个单向函数 $H$，它满足：

• 计算 $H(x)$ 是容易的；
• 但给定 $y$，要找到 $x$ 使得 $H(x)=y$ 是困难的。

一个标准例子是取 $H$ 为某个密码学哈希函数，然后令关系 $\mathcal{R}$ 为其原像关系：

• 密钥生成：私钥 $x$ 随机采样，公钥为 $y=H(x)$。
• 签名生成：对于某个消息 $m$，签名者使用零知识证明系统来证明自己知道某个私有 $x$，使得 $H(x)=y$，其中 $y$ 是公钥。
  • 利用 Fiat-Shamir 转换，可以高效地将消息 $m$ 融入证明中。让证明者发送的第一条消息就是该消息 $m$，然后协议照常继续执行。
  • 这样得到的就是一种“与消息绑定的知识证明（message-dependent proof of knowledge）”：签名者证明其知道某个使公钥成立的原像，但该证明仅对某个特定消息 $m$ 有效。
  • 注意，验证者生成的每个挑战都是依赖于该初始消息 $m$ 的，因此这个签名不能在其他消息上复用。
• 签名验证：验证者首先检查证明中包含的消息是否等于 $m$，然后验证关联的零知识证明是否有效。

目前已经有多个具体签名方案基于这一思想被提出，例如：

• 2016年论文 ZKBoo: Faster Zero-Knowledge for Boolean Circuits，开源代码实现见：
  • https://github.com/Sobuno/ZKBoo（C语言））
• 2017年论文 Picnic（Post-Quantum Zero-Knowledge and Signatures from Symmetric-Key Primitives），开源代码实现见：
  • https://github.com/Microsoft/Picnic（C语言）
  • https://github.com/isec-tugraz/fish-begol（C语言+Python）
• 2018年论文 KKW18（Improved Non-Interactive Zero Knowledge with Applications to
  Post-Quantum Signatures）
• 2023年论文 FAEST（Publicly Verifiable Zero-Knowledge and Post-Quantum Signatures
  From VOLE-in-the-Head），开源代码实现见：
  • https://github.com/faest-sign/faest-rs/tree/crypto-2023（Rust）

值得注意的是，Ligero 零知识证明系统也可以被看作是对 MPC-in-the-Head 转换的一种优化实现：

• Ligero通过使用对主动攻击者安全的 MPC 协议，成功实现了次线性（sub-linear）证明大小。
• 开源代码见：https://github.com/ligeroinc/ligero-prover（C++和WebAssembly）

参考资料

[1] zkSecurity团队2025年2月20日博客 A Gentle Introduction to the MPC-in-the-Head Transformation