当前位置：首页 > news >正文

前缀和

news 2025/8/8 9:02:55

1 【模板】前缀和

2 【模板】二维前缀和

3 寻找数组的中心下标

4 除自身以外数组的乘积

5 和为 K 的子数组

6 和可被 K 整除的子数组

7 连续数组

8 矩阵区域和

总结

在有些场景中，需要我们频繁去获取某一段连续区间的和或者积，如果我们每一次都去遍历这段区间求的话，时间复杂度过高，那么我们其实可以预处理一下，每一个[0,i]区间的所有元素的和或者积记录在一个数组的 prev[i] 中，这个数组就是前缀和数组。当然前缀和数组中不一定只保存和/积，也不一定是一个一维数组，它需要根据场景来确定。同时相对应的，除了前缀和数组，还有后缀和数组，back[i] 记录[i,n-1]区间的元素和，有了这两个数组，我们就很容易能够求出任意一个连续区间的和，比如 sum([i,j]) = prev[j] - prevc[i-1] 或者 back[j] - back[i+1]。

1 【模板】前缀和

【模板】前缀和_牛客题霸_牛客网

题目解析：题目给定一个长度为n的数组，有m次查询操作，给定l和r，我们需要对每一次查询数组[l,r]的元素和。

暴力解法：每一次查询都遍历数组的[l,r]进行求和。

那么本题我们使用前缀和来求就很简单了,其实前缀和数组我们可以用动态规划的方式表示出来。

dp[i] 表示 [0,i]的区间的元素和，那么状态转移方程就是：dp[i] = dp[i-1] + nums[i]，我们需要初始化dp[0]。当然也可以使用虚拟位置来省去初始化。

每一次查询的结果 sum([l,r]) = dp[r] - dp[l-1]。

代码如下：

#include <iostream>
#include <vector>
using namespace std;int main() {int n , m , x , l , r;cin>>n>>m;vector<long long> nums(n) , dp(n);for(int i = 0 ; i < n ; ++i){cin>>nums[i];if(i == 0) dp[0] = nums[0];else dp[i] = dp[i-1] + nums[i];}while(m--){cin>>l>>r;cout<<dp[r-1] - (l == 1 ? 0 : dp[l-2]) << endl;}return 0;
}

由于题目要求的是第l个元素到第r个元素的和，也就是[l-1,r-1]。

同时我们需要考虑特殊情况就是l == 1 ，也就是 l-1 ==0，由于我们没有开额外空间，并没有空数组的和，此时需要特殊判断。

2 【模板】二维前缀和

【模板】二维前缀和_牛客题霸_牛客网

题目解析：给定一个 n*m 的二维矩阵，有q次查询参数为 x1,x2,y1,y2，每一次查询需要数组，求出由(x1,y1),(x1,y2),(x2,y1),(x2,y2)所围成的矩阵的元素和。

暴力解法：每一次查询都遍历这个范围内的数据进行求和。

本题可以使用二维的前缀和数组来求，为了减少对边界位置的初始化，我们可以多开一行和一列。

dp[i][j] 表示(0,0)为左上角，(i-1,j-1)为右下角的矩形的元素和。

那么dp[i][j] = nums[i][j] + dp[i-1][j] + dp[i][j-1] - dpi-1][j-1]。

我们需要求的是左上角为(x1-1,y1-1)，右下角为(x2-1,y2-1)的矩形的元素和。sum = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]。

这两个公式我们都可以画图表示出来，其实就是简单的面积切割，这里不过多讲解。

代码如下：

#include <iostream>
#include <vector>
using namespace std;int main() {int n,m,q,x1,x2,y1,y2,num;cin>>n>>m>>q;vector<vector<long long>> dp(n+1,vector<long long>(m+1));for(int i = 0 ; i < n ; ++i){for(int j = 0 ; j < m ; ++j){cin>>num;  //输入nums[i][j]//要填的位置是dp[i+1][j+1]dp[i+1][j+1] = num + dp[i+1][j] + dp[i][j+1] - dp[i][j];}}while(q--){cin>>x1>>y1>>x2>>y2;  //x1,x2是行数，需要-1才是行下标，y1,y2是列数，需要减1才是列下标long long res = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]; cout<<res<<endl;}return 0;
}

3 寻找数组的中心下标

724. 寻找数组的中心下标 - 力扣（LeetCode）

题目解析：给定一个数组，找到一个下标i，使得i下标前面的元素总和与 i下标后面的元素总和相等。

暴力解法：枚举每一个下标，对前后进行求和，判断是否相等。

本题我们可以使用一个前缀和数组dp,dp[i]表示[0,i)的元素和。那么对于任意一个下标i，他的前面的元素总和为 dp[i] ，他的后面的元素的总和为 dp[n-1] - dp[i+1]，如果两者相等，那么i就是中心下标。

代码如下：

class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();vector<int> dp(n+1);for(int i = 0 ; i < n ; ++i) dp[i+1] = dp[i] + nums[i];for(int i = 0 ; i < n ; ++i){if(dp[i] == dp[n] - dp[i+1]) return i;}return -1;}
};

4 除自身以外数组的乘积

238. 除自身以外数组的乘积 - 力扣（LeetCode）

题目解析：题目要求我们求出数组除去每一个元素的剩余元素的乘积。

题目要求我们不要使用除法，因为可能出现除0错误。

数组中除去nums[i]的元素乘积我们可以分成两部分看[0,i) 以及 [i+1,n) ，这两个区间的元素就是数组除去i位置的元素，那么这两个区间的元素乘积就是我们需要的结果。

那么我么可以使用一个前缀数组 prev 和后缀数组back。

prev[i] 表示 [0,i)区间的元素乘积，而back[i] 表示([i,n)区间元素的乘积。

那么 res[i] = prev[i] * back[i+1]。

代码如下：

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> prev(n + 1) , back(n + 1) , res(n);prev[0] = back[n] = 1; //由于是乘法，我们需要初始化为1for(int i = 1 ; i <= n ; ++i) prev[i] = prev[i-1] * nums[i-1];for(int i = n - 1 ; i >= 0 ; --i){back[i] = nums[i] * back[i+1];}for(int i = 0 ; i < n ; ++i) res[i] = prev[i] * back[i+1];return res;}
};

如果我们想要时空复杂度更优，那么可以省去后缀和数组，使用一个变量来统计，同时填写res的循环可以和计算后缀和的循环放在一起。

5 和为 K 的子数组

560. 和为 K 的子数组 - 力扣（LeetCode）

题目解析：要求我们返回和为k的子数组的数量。

暴力解法：枚举所有的子数组，然后遍历该子树组求出数组和。

我们可以使用前缀和数组来优化掉子数组的遍历求和过程，而是直接使用前缀和中的数据进行快速求和。

本题我们可以使用一个二维的前缀和数组dp。

dp[i][j] 表示区间[i,j]的子数组元素和。那么我们在填表过程中就可以顺便记录一下和为k的子数组数量。

dp[i][j] = dp[i][j-1] + nums[j]。

但是由于数据量较大，O(N^2)的时间复杂度可能会超时，所以我们需要想出一种更快速的方式，参考动态规划的思路，我们如果要找以 i 位置为结尾的和为k的子数组数量，我们能够知道[0,i]的前缀和sum，那么我们其实就是要找到有多少个左端点x，使得[x,i]这个区间的子数组的和为 k，那么我们不难推出，只需要[0,x-1]区间的和为 sum - k ，那么就能够使得 [x,i]的子数组和为k。

换句话说，其实我们是在使用 dp[i] - dp[j-1] 来求 [j ,i] 的元素和，我们在遍历过程中能够用一个变量sum记录 dp[i] ，那么我们只需要找到前面出现的前缀和中，有多少个前缀和等于 sum - k 就行了，在这里我们可以使用哈希表来保存前缀和的值以及出现的次数，就能快速求出前面出现过多少次对应的前缀和。

特殊情况：sum == k 的时候，其实也是一个和为k的子数组，此时我们需要去哈希表中找到和为0的前缀和，但是我们并没有预先放入这种情况，所以在实际遍历数组的时候，我们需要预先放进一个前缀和为0，相当于记录 [0,0)的前缀和。

class Solution {
public:int subarraySum(vector<int>& nums, int k) {int sum = 0 , res = 0;unordered_map<int,int> hash;hash[0] = 1;for(auto x : nums) {sum += x;res += hash[sum - k];hash[sum]++;}return res;}
};

6 和可被 K 整除的子数组

974. 和可被 K 整除的子数组 - 力扣（LeetCode）

题目解析：题目要求我们求出和可被k整除的子数组的数量。

本题其实和上一题类似，只不过上一题是和为k，而这一题只需要和能够被k整除就行了。如果我们用两层循环来求每一个区间的数组和，一定会和上一个题一样超时，所以我们还是需要利用哈希表来做。

我们遍历数组的时候会记录当前的前缀和 sum ，那么以i位置为结尾的和能够被k整除的子数组有多少个呢？就取决于前面出现的前缀和x中，有多少前缀和x能够满足 (sum - x)%k==0。

那么怎么去找这些前缀和呢？

我们可以先学习一个数学定理：同余定理： (a-b) % x ==0 ，说明a和b要么都能够被x整除，要么就是a和b对x的余数相同，其实两者都可以归为一类就是： a%x == b%x。

所以如果我们要找满足 (sum - x)%k==0的x的数量时，其实可以转换为找前面出现的前缀和中，有多少个前缀和x%k==sum%k。

但是由于计算机中的取余运算，对于负数取余的结果还是负数，比如： -3%2 = -1。我们如果要将负数的取余结果也转换为正数的话，那么可以这样做: (x % k + k) % k 。不管x是正数还是负数，最终的取余的结果都是正数。

细节：我们还是需要先讲一个0加入到哈希表，表示当前数组不需要删除任何前缀数组就能够使和被k整除。

代码如下：

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {int sum = 0 , n = nums.size() , res = 0;unordered_map<int,int> hash;hash[0] = 1;for(auto x : nums){sum += x;res += hash[(sum % k + k) % k];hash[(sum % k + k) % k]++;}return res;        }
};

7 连续数组

525. 连续数组 - 力扣（LeetCode）

题目解析：给定一个只含0和1的数组，要求我们求出0和1的数量相等的最长子数组。

暴力解法还是枚举所有的子数组来判断。

如果我们直接做这个题的话，发现使用前缀和无从下手，但是如果我们把数组中所有的0换成-1，那么-1和1的数量相等，就意味着该子数组的和为0，这样一来我们就能够将题目转换为求和为0的最长子数组的长度，而要求固定和的子数组，我们已经有过经验了，也就是前面的第5题。

但是本题需要优化一下就是，我们要的是最长的子数组的长度。对于当前的前缀和sum，我们需要找到出现过的前缀和x使得 sum - x == 0，但是这样的x可能存在多个，由于我们需要的是最长的子数组的长度，也就是当前的前缀数组[0,i] 要减去对应的前缀数组，那么对应的前缀数组自然是越小越好，我们只会用到和为 sum 的长度最小的那么前缀数组。

那么我们在哈希表中存储的其实是sum以及对应的前缀数组[0,i]下标i，当本次求出的sum已经在哈希表中出现过时，那么我们并不需要将这个sum存入哈希表。

代码如下：

class Solution {
public:int findMaxLength(vector<int>& nums) {int sum = 0 , res = 0 , n = nums.size();unordered_map<int,int> hash; //存储前缀和以及对应的最小的前缀数组的结尾下标hash[0] = -1;for(int i = 0 ; i < n ; ++i){if(nums[i] == 0) sum--;else sum ++;if(hash.count(sum)){res = max(res , i - hash[sum]);}else hash[sum] = i;}return res;}
};

8 矩阵区域和

1314. 矩阵区域和 - 力扣（LeetCode）

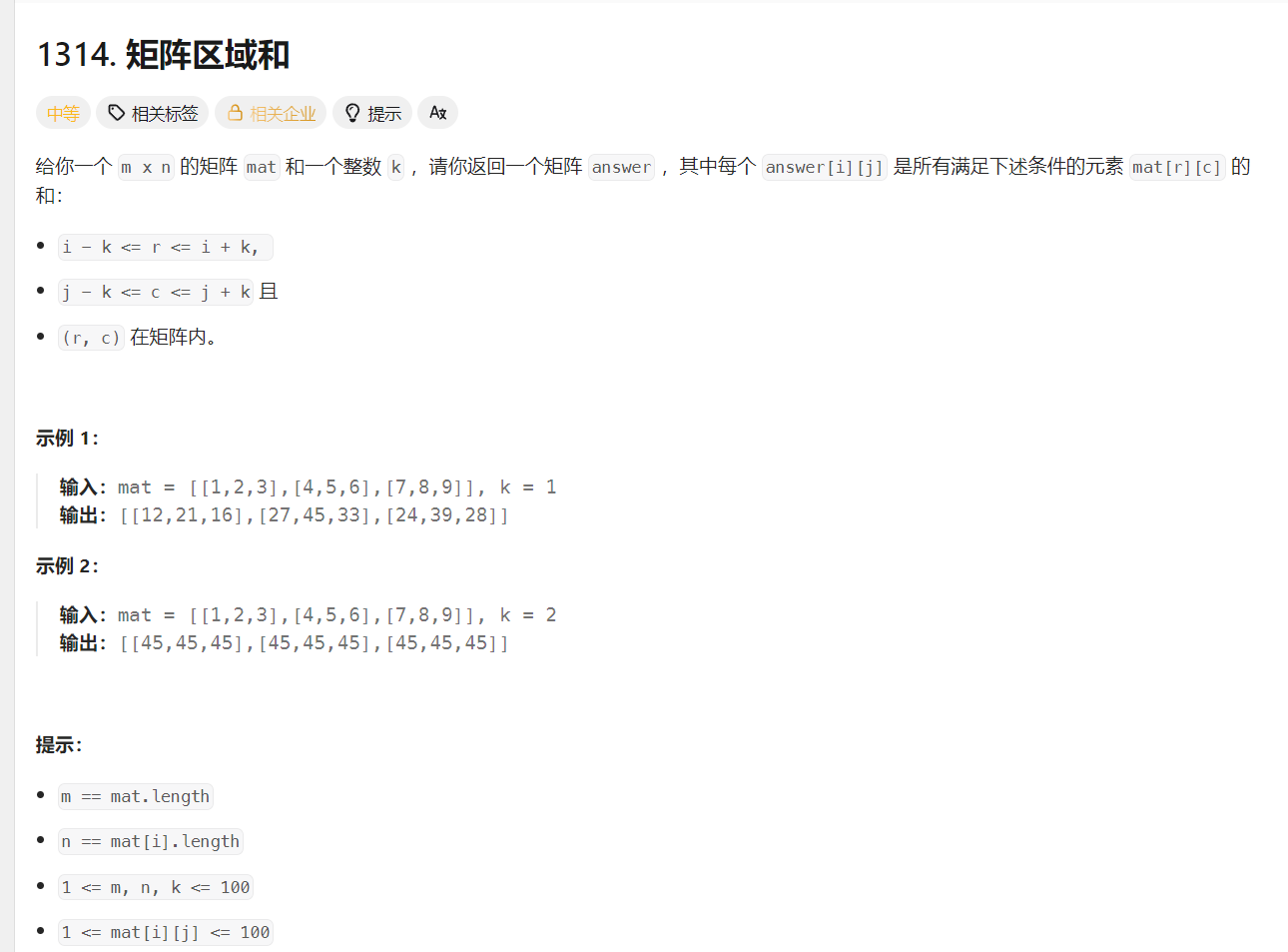
题目解析：题目给定一个m*n的矩阵，要我们求出每一个位置(i,j)，满足上述条件的位置的元素的和。

本题其实就是一个求矩阵和的问题，转换为二位前缀和就很简单，那么题目的条件具体怎么看呢？

对于一个位置(i,j)，其实就是求出如图的矩形内的元素和:

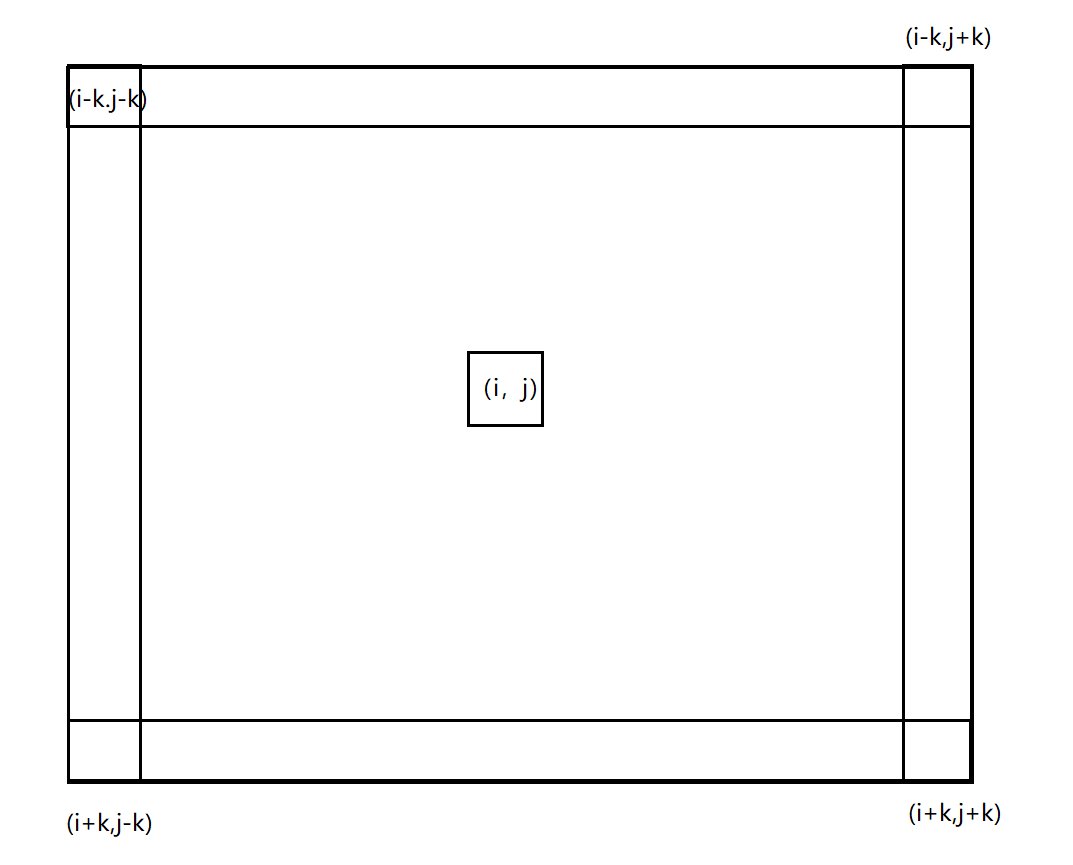其实就是求出(i-k,j-k) 和 (i+k,j+k)之间的矩形的元素和。但是需要注意的时i-k,j-k,i+k,j+k都有可能越界，越界的时候我们就只需要计算到边界就行了，我们可以把这些值看成第2题中的x1，y1，x2，y2。

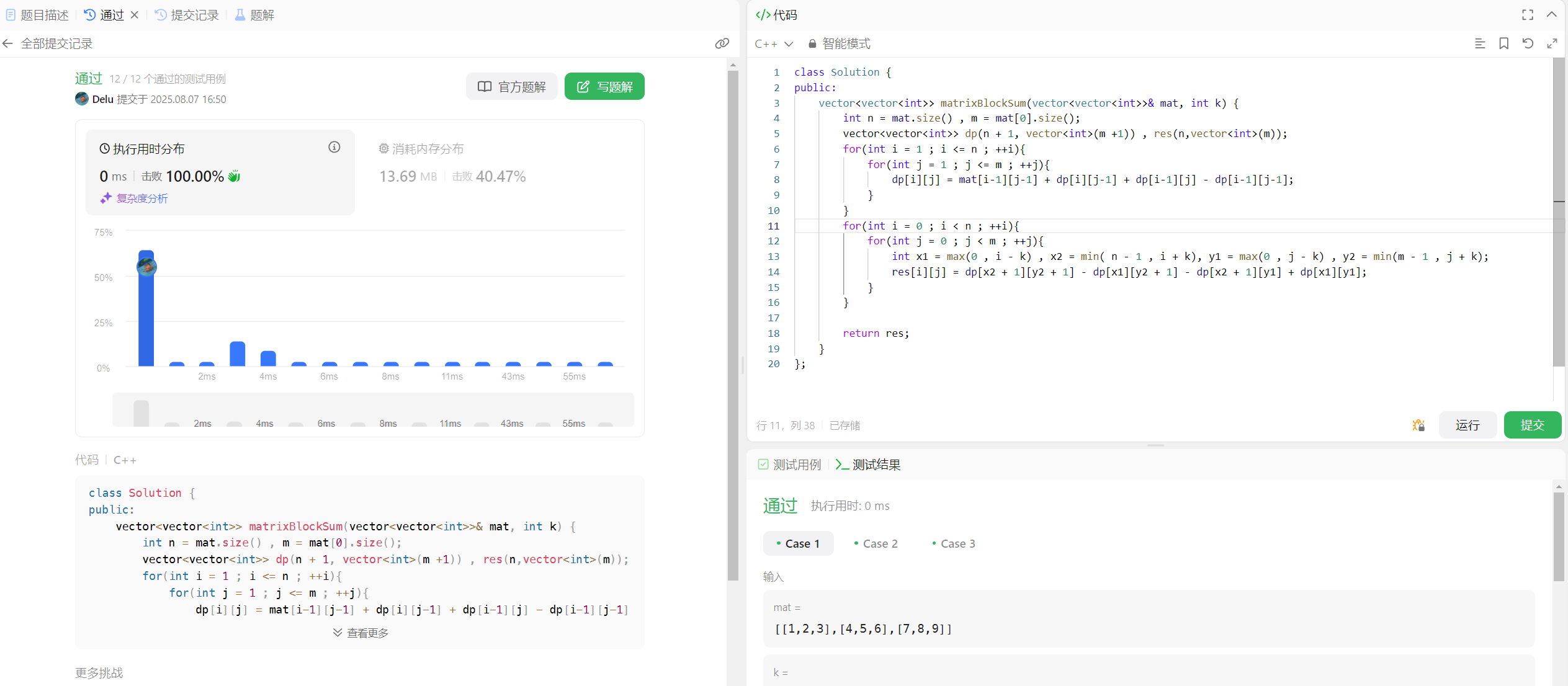
代码如下：

class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int n = mat.size() , m = mat[0].size();vector<vector<int>> dp(n + 1, vector<int>(m +1)) , res(n,vector<int>(m));for(int i = 1 ; i <= n ; ++i){for(int j = 1 ; j <= m ; ++j){dp[i][j] = mat[i-1][j-1] + dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1];}}for(int i = 0 ; i < n ; ++i){for(int j = 0 ; j < m ; ++j){int x1 = max(0 , i - k) , x2 = min( n - 1 , i + k), y1 = max(0 , j - k) , y2 = min(m - 1 , j + k);res[i][j] = dp[x2 + 1][y2 + 1] - dp[x1][y2 + 1] - dp[x2 + 1][y1] + dp[x1][y1];}}return res;}
};