当前位置：首页 > news >正文

四边形面积

news 2025/8/8 7:17:29

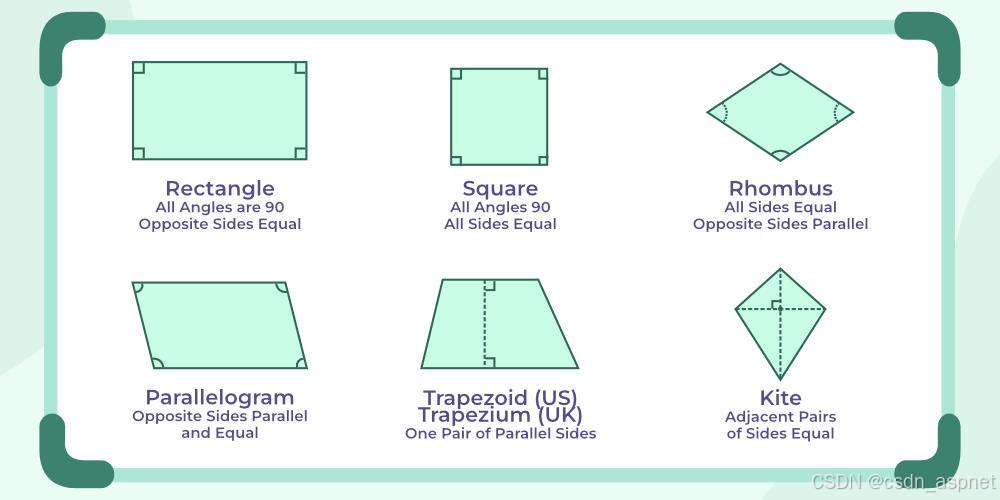
四边形是具有四条边、四个角和四个顶点的多边形。它是一个二维图形，由四个点（顶点）和直线（边）连接而成。四边形的边可以相等，也可以不相等。根据角、边和对角线的性质，可以定义出各种类型的四边形，其中一些类型如下：

长方形
正方形
菱形
平行四边形
梯形
风筝

四边形面积：

四边形的面积是四边形边界内的空间，或者换句话说，是四边形边所包围的空间。

用一条对角线把四边形分成两个三角形，就能求出它的面积。已知对角线的长度和两个三角形的高，则四边形的面积为：

A = ½ × 对角线 × （高度总和）

注意：四边形的面积以平方单位测量，例如m 2、in 2、cm 2等。

四边形面积公式

在四边形ABCD中，对角线BD的长度为d。ABCD可以被对角线BD分成两个三角形ΔABD和ΔBCD。计算四边形ABCD的面积，我们需要计算各个三角形的面积，然后将它们相加。但计算三角形的面积时，必须知道它的高度。假设三角形ABD和BCD的高度分别为h1和h2。

三角形ABD的面积= (1/2) × d × h 1。
三角形BCD的面积= (1/2) × d × h 2。

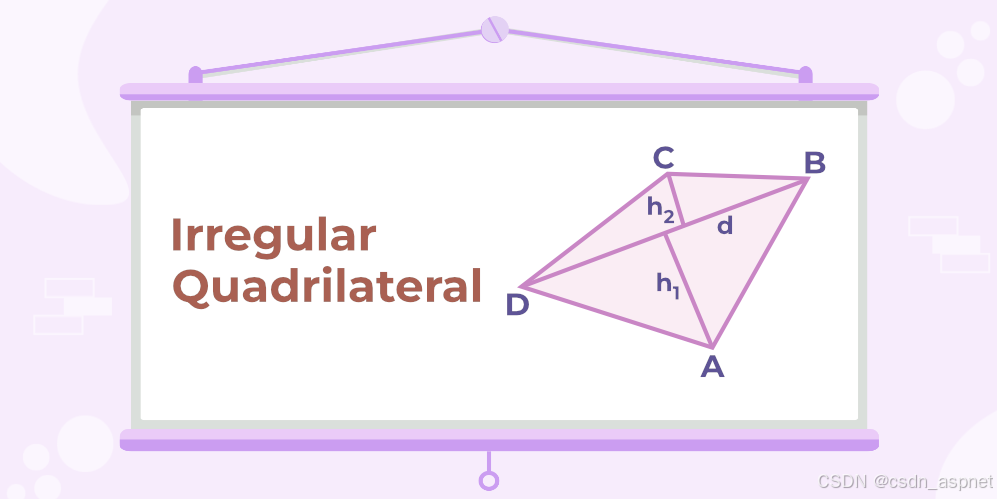
由图可知，四边形ABCD的面积=ΔABD的面积+ΔBCD的面积。

四边形ABCD的面积= (1/2) × d × h 1 + (1/2) × d × h 2 = (1/2) × d × ( h 1 + h 2 )。

因此，求四边形面积的公式是，

四边形面积 = (1/2) × 对角线 × (高度之和) = (1/2) × d × ( h 1 + h 2 )

有顶点的四边形面积

如果给定四边形的顶点，假设 A(x 1 , y 1 )、B(x 2 , y 2 )、C(x 3 , y 3 ) 和 D(x 4 , y 4 ) 是四边形 ABCD 的顶点。

然后使用两种不同的方法计算其面积：

鞋带定理
用三角形计算面积

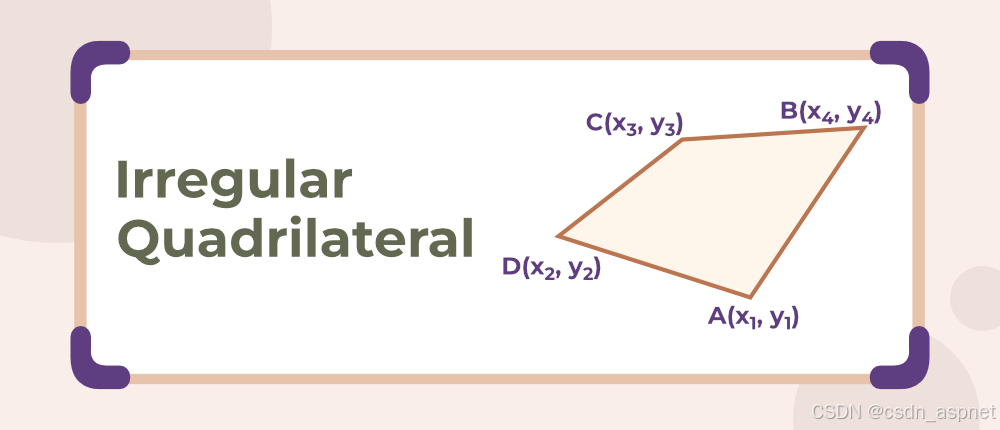
使用坐标几何（或鞋带定理）计算四边形面积

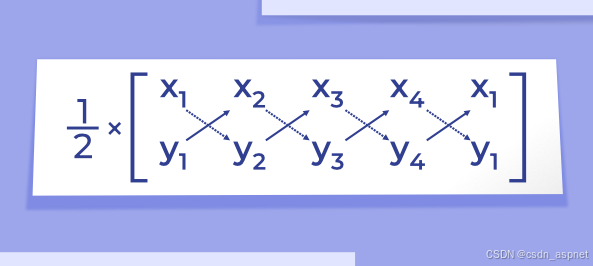
按照箭头方向，添加对角线积，即 x 1 y 2、x 2 y 3、x 3 y 4和 x 4 y 1。

(x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 1 )….(i)

现在，沿着虚线箭头添加对角线积，即 x 2 y 1、x 3 y 2、x 4 y 3和 x 1 y 4。

(x 2 y 1 + x 3 y 2 + x 4 y 3 + x 1 y 4 )….(ii)

现在，从 (i) 中减去公式 (ii)，然后将结果乘以 1/2。

(1/2) × [(x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 1 ) – (x 2 y 1 + x 3 y 2 + x 4 y 3 + x 1 y 4 )]

因此，当给定顶点时，四边形的面积公式为：

利用三角形面积求四边形面积

该方法将给定的四边形分成两个三角形，然后分别求每个三角形的面积。最后，将两个三角形的面积相加，得到四边形的最终面积。

四边形ABCD的面积=三角形ABD的面积+三角形BCD的面积

具有顶点 P(x 1 , y 1 )、Q(x 2 , y 2 ) 和 R(x 3 , y 3 ) 的三角形的面积由下式给出

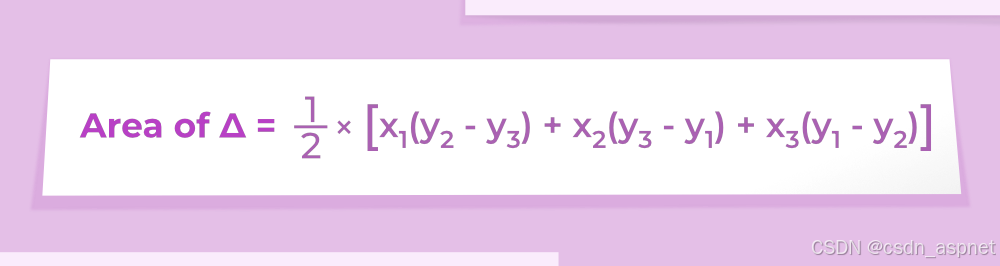
用 Bretschneider 公式计算四边形面积

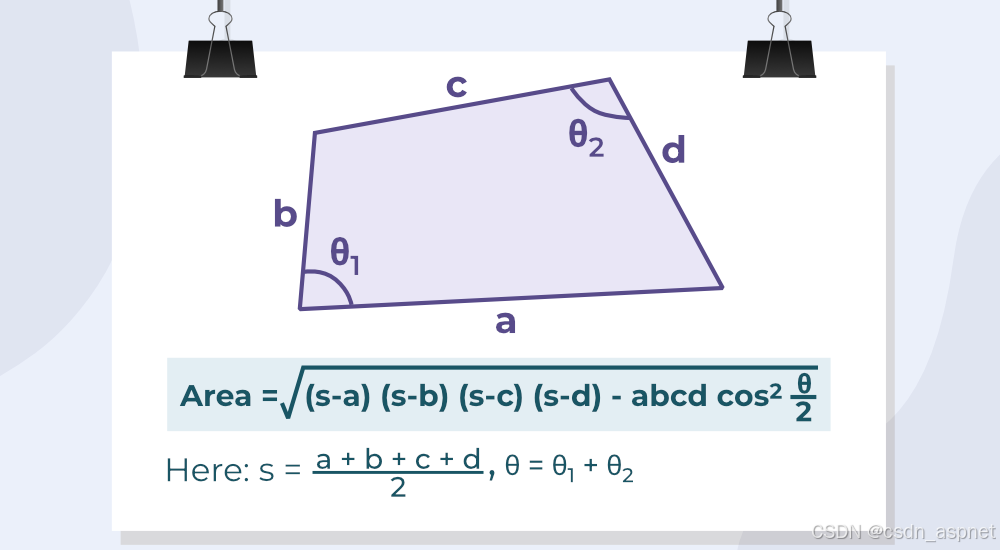
当给定两个对角和四边形的所有边时，我们可以使用Bretschneider 公式计算其面积，该公式是 Heron 四边形公式的扩展，如下所示：

常见四边形的面积公式

一些特定的四边形非常常见，在我们的日常生活中使用，它们的面积公式在下面的文章中解释：

正方形的面积

正方形是长方形的一种特殊情况，四条边相等，且所有边都互相平行。正方形的对角线互相垂直平分。

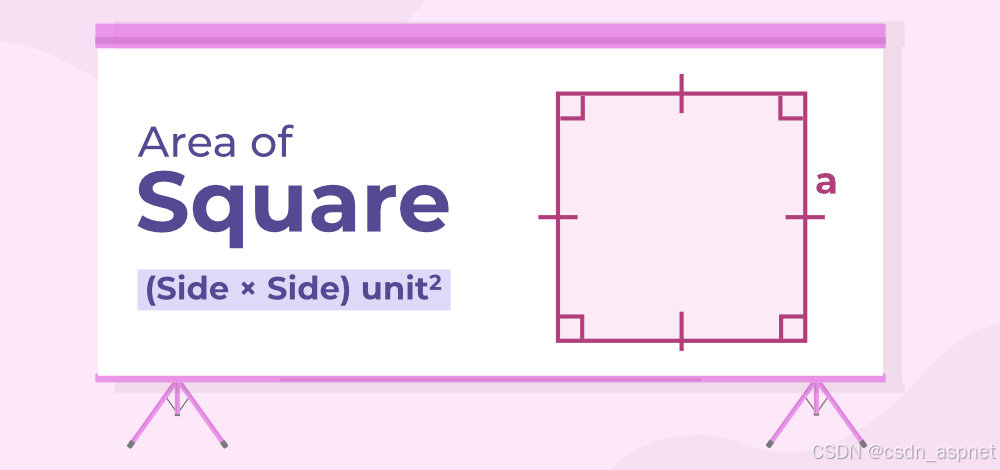
：正方形面积

矩形面积

矩形是具有四条边的封闭图形，其中相对的边相等且彼此平行，并且矩形的对角线以 90 度角平分。

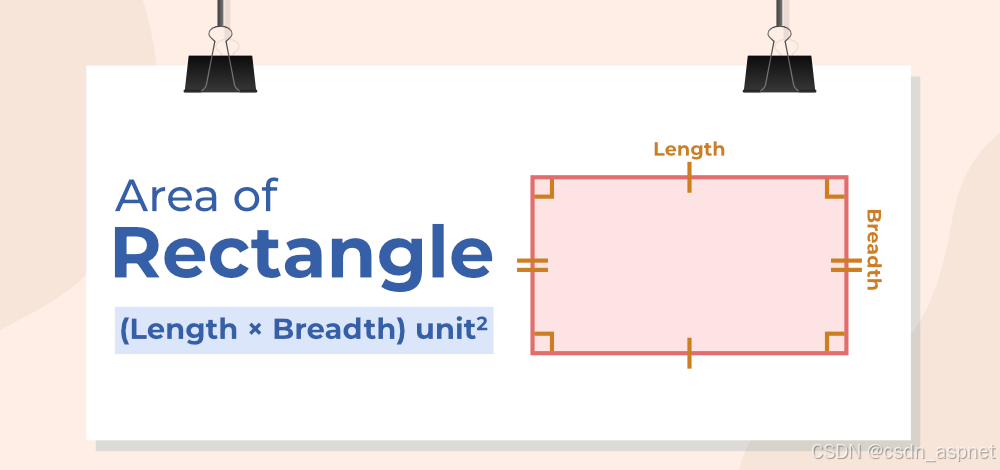
：矩形面积

菱形的面积

菱形是正方形的一个特例，它的四条边和对角都相等，对边平行，邻角和等于 180 度。

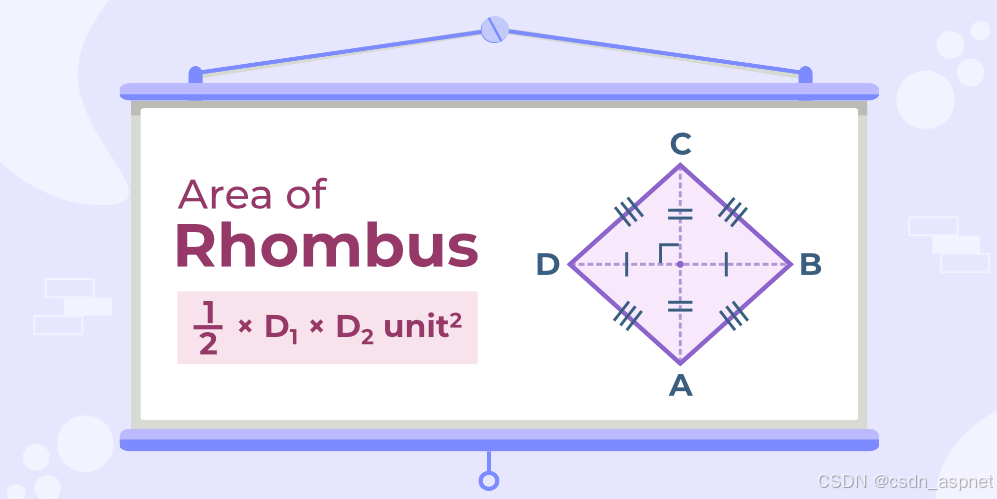
其中 D1 和 D2 是菱形对角线的长度。

：菱形面积

平行四边形的面积

对边相等且互相平行的四边形称为平行四边形。平行四边形的对角线互相平分，对角相等，平行四边形两个相邻角之和等于 180 度。

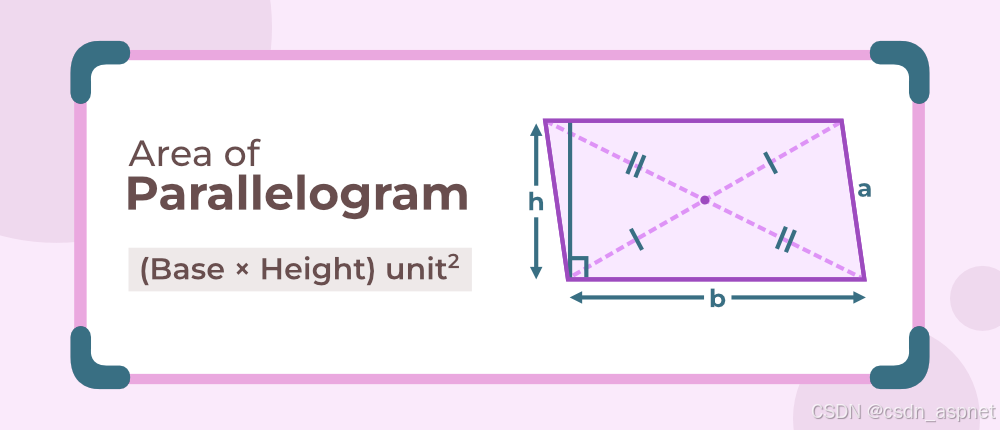
：平行四边形的面积

梯形面积

这个四边形与其他四边形有些不同，因为梯形只有一对对边平行，邻边互补，对角线以相同的比例平分。

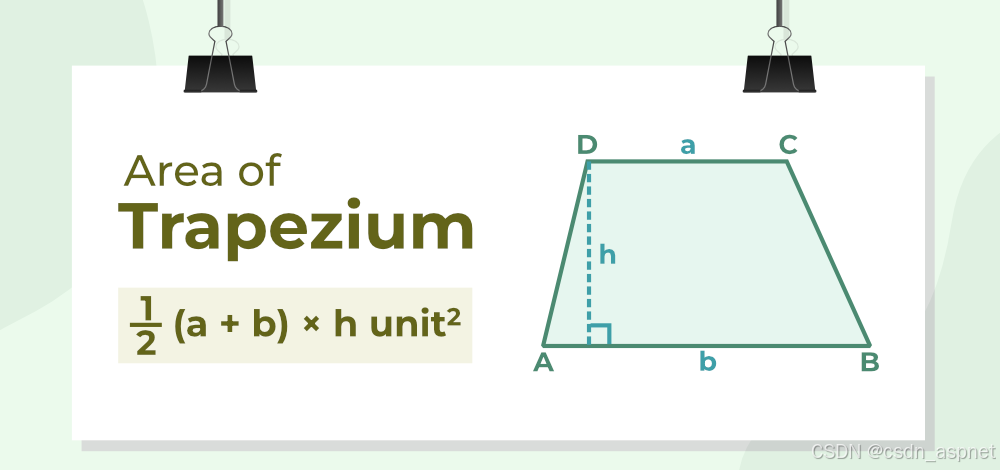
梯形面积

：梯形面积

风筝面积

风筝形是一种特殊的四边形，其每对相邻边全等，但相对边不全等。在这种情况下，风筝形的最大对角线平分最小对角线。

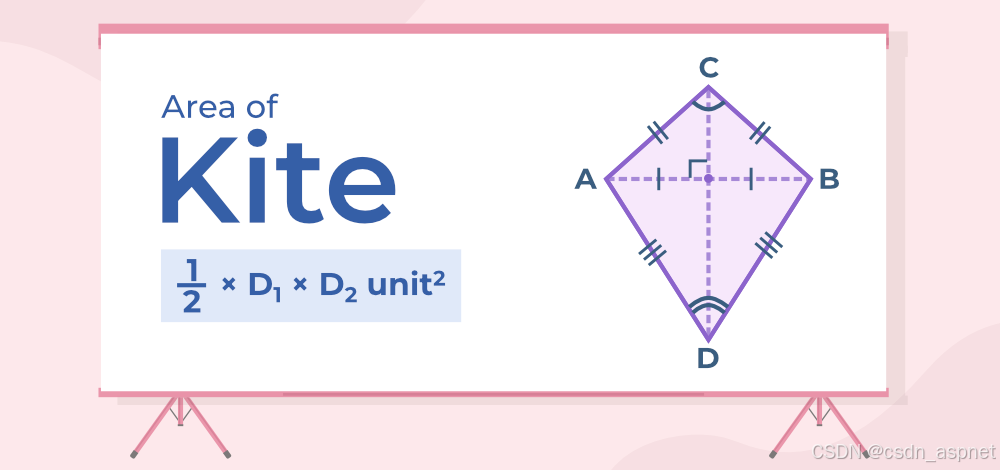
其中，D1 = 风筝的长对角线（CD），D2 = 风筝的短对角线（AB）

另请阅读：风筝的面积

四边形面积解题示例

例 1：当四边形 ABCD 的顶点分别为 (1, 2)、(5, 6)、(4, −6) 和 (−5, 2) 时，求其面积。

解决方案：

设 A(1, 2)、B(5, 6)、C(4, -6) 和 D(-5, 2) 为四边形 ABCD 的顶点。

A(1, 2) = (x 1 , y 1 ), B(5, 6) = (x 2 , y 2 ), C(4, -6) = (x 3 , y 3 ), D(-5, 2) = (x 4 , y 4 )

我们知道，

四边形面积 = (1/2) × [(x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 1 ) – (x 2 y 1 + x 3 y 2 + x 4 y 3 + x 1 y 4 )]

⇒ 四边形面积 = (½).{[1(6) + 5(-6) + 4(2) + (-5)2] – {[5(2) + 4(6) + (-5)(-6) + 1(2)]}
⇒ 四边形面积 = (½).[(6 – 30 + 8 – 10) – (10 + 24 + 30 + 2)]
⇒ 四边形面积 = (½)[-26 - 66]
⇒ 四边形面积 = 92/2（面积永远不为负值）
⇒ 四边形面积 = 46 单位2

例 2：设梯形的高度为 5 厘米，AB 和 CD 分别为 10 厘米和 6 厘米，求梯形的面积。

解决方案：

已知AB=10cm，CD=6cm，高=5cm

根据公式，

梯形面积 = (1/2) h (AB + CD)

⇒ 梯形面积 = 1/2 x 5 x (10 + 6)

⇒ 梯形面积 = 40 cm2

例3：一只风筝，最长对角线为20cm，最短对角线为10cm，求其面积。

解决方案：

最长对角线的长度，D 1 = 20 厘米

最短对角线的长度，D2 = 10厘米

所以，风筝的面积=1/2 x D 1 x D 2

⇒ 风筝面积 = 1/2 x 20 x 10
⇒ 风筝面积 = 100 cm2

例 4：计算平行四边形，底边长为10米，高为15米。

解决方案：

已知底边 = 10 米，高 = 15 米，
平行四边形的面积 = 底边 × 高

⇒ 平行四边形的面积 = 10 x 15
⇒ 平行四边形的面积 = 150 m 2

例 5：已知菱形的边长为 120 米，如果另一条对角线的长度为 12 米，则求其中一条对角线的长度。

解决方案：

因为我们知道，
菱形面积 = (1/2) x 对角线1 x 对角线2

把所有已知值放在一起，我们得到
120 = (1/2) x 对角线 1 x 对角线 2

对角线 2 = 20 米

四边形面积练习题

问题 1：求底边为 6 厘米、高为 8 厘米的平行四边形的面积。
问题 2：一个长方形的长为 10 米，宽为 4 米。计算它的面积。
问题 3：计算底边长分别为 6 厘米和 10 厘米、高为 5 厘米的梯形的面积。
问题 4：已知菱形的对角线长为 8 厘米和 10 厘米，求菱形的面积。
问题 5：已知一个不规则四边形的顶点坐标：A(0,0)、B(4,3)、C(6,7)、D(2,5)。计算它的面积。